固体颗粒对半球扰动尾迹影响的实验研究1)
2020-06-10张艳涛高天达陈文义
张艳涛 孙 姣 高天达 范 赢 陈文义,2)
∗(河北工业大学过程装备与控制工程系,天津 300130)
†(河北工业大学工程流动与过程强化研究中心,天津 300130)
引言
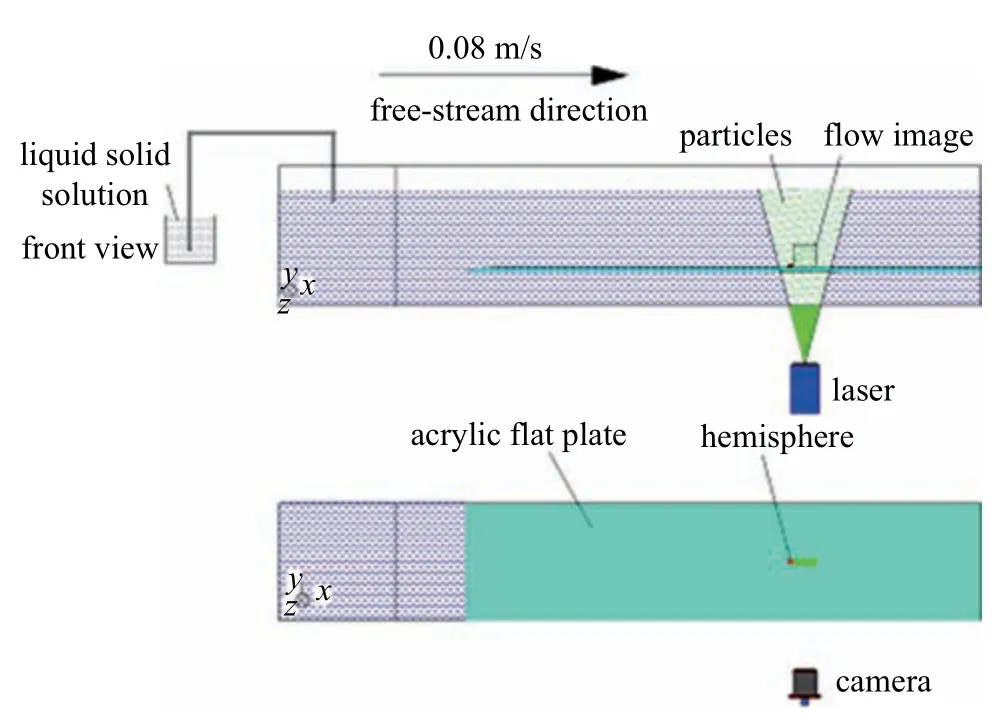
液固两相流广泛存在于化工、核能、动力等设备中,液体和颗粒相互作用引起质量和动量的传递与能量的扩散[1-3],壁面约束产生的近壁复杂的相干结构对传递和扩散具有重要的影响,自然界及工程中的壁面多为粗糙壁面,粗糙元加速边界层转捩并产生与湍流边界层相似的相干结构[4-6],半球粗糙元具有普适性,以半球粗糙元作为模型开展固体颗粒作用下半球尾迹研究,有利于揭示流动机理及工程应用.
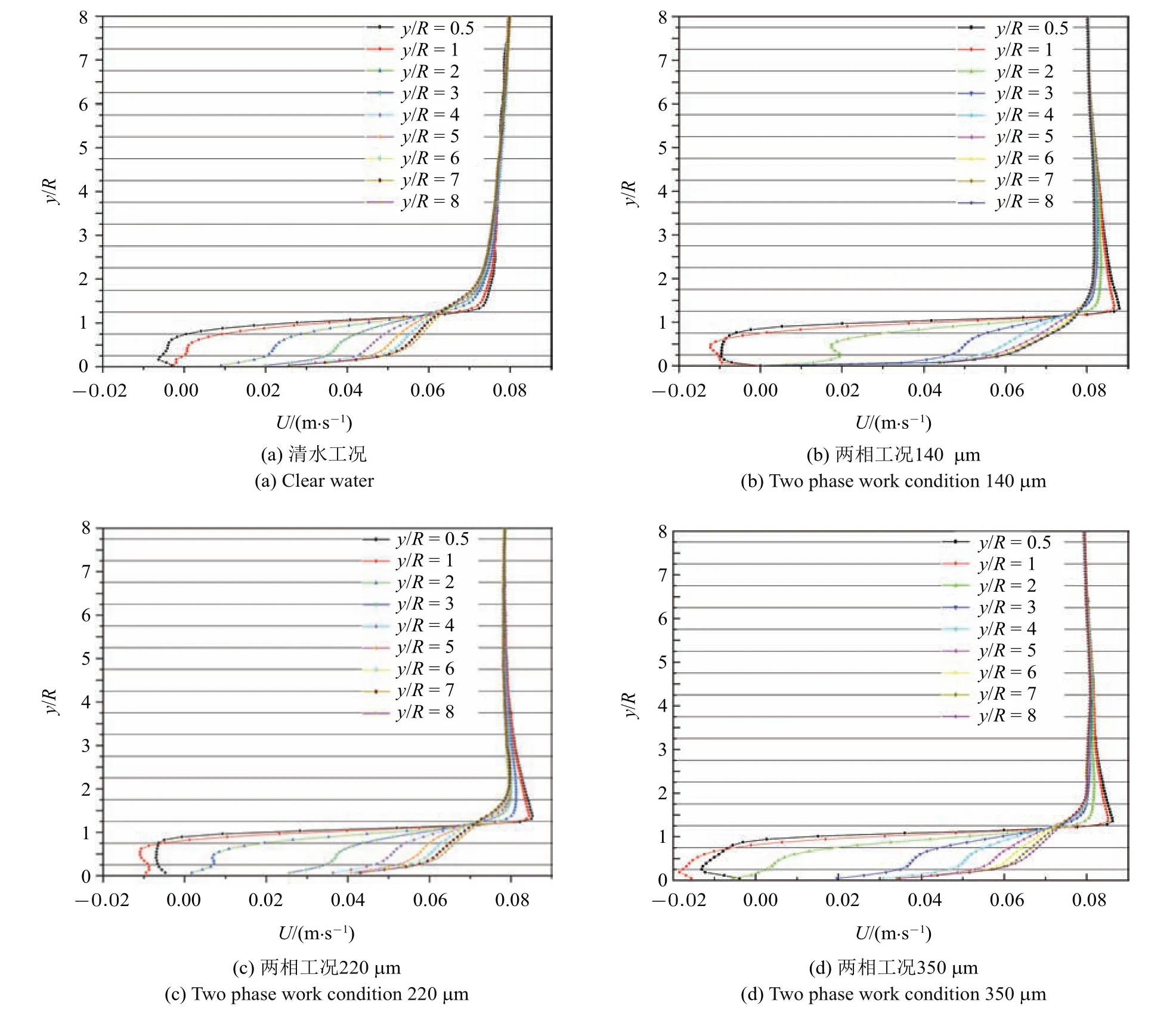
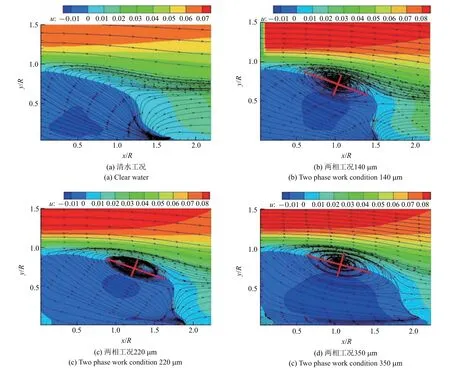
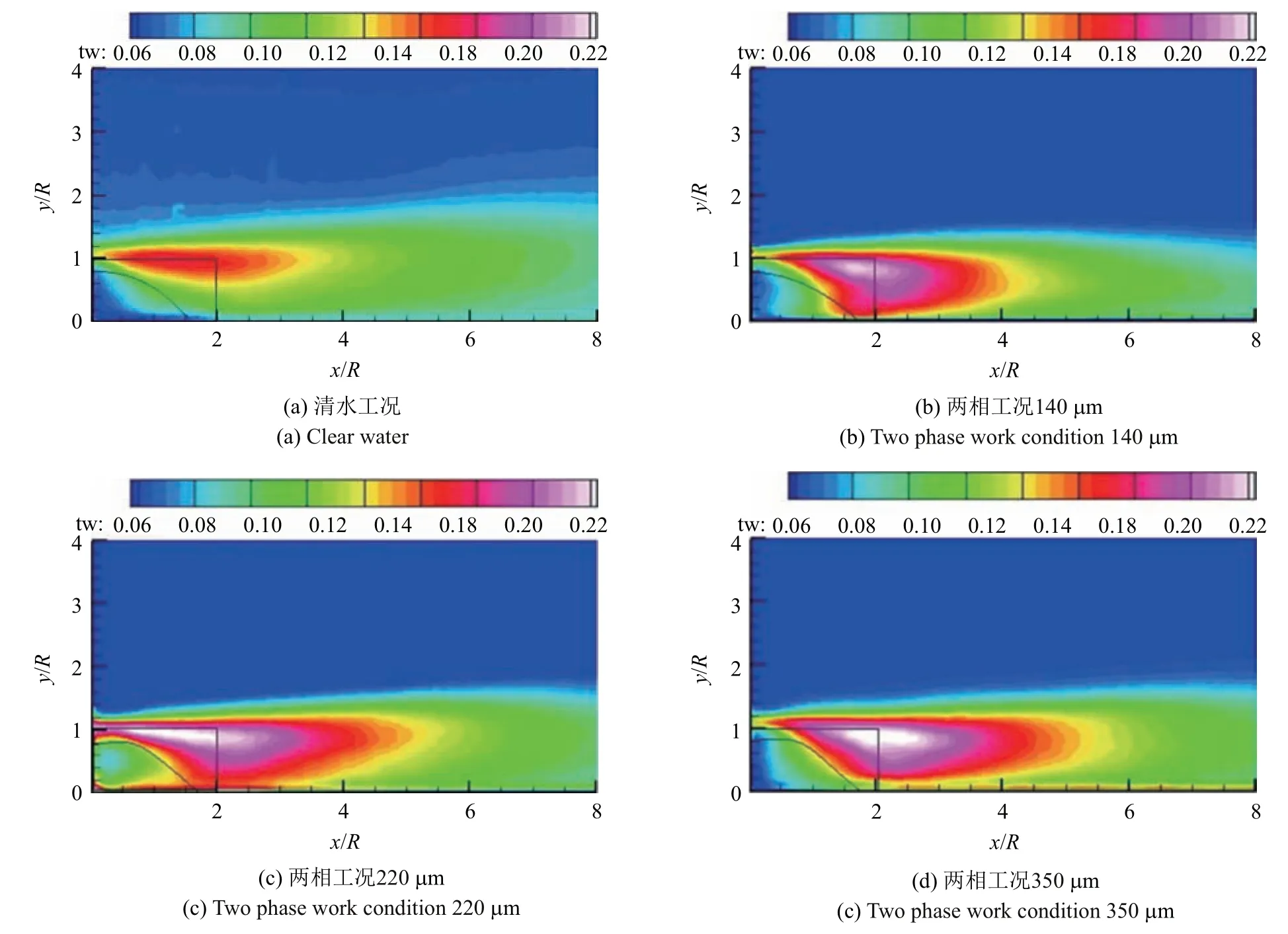
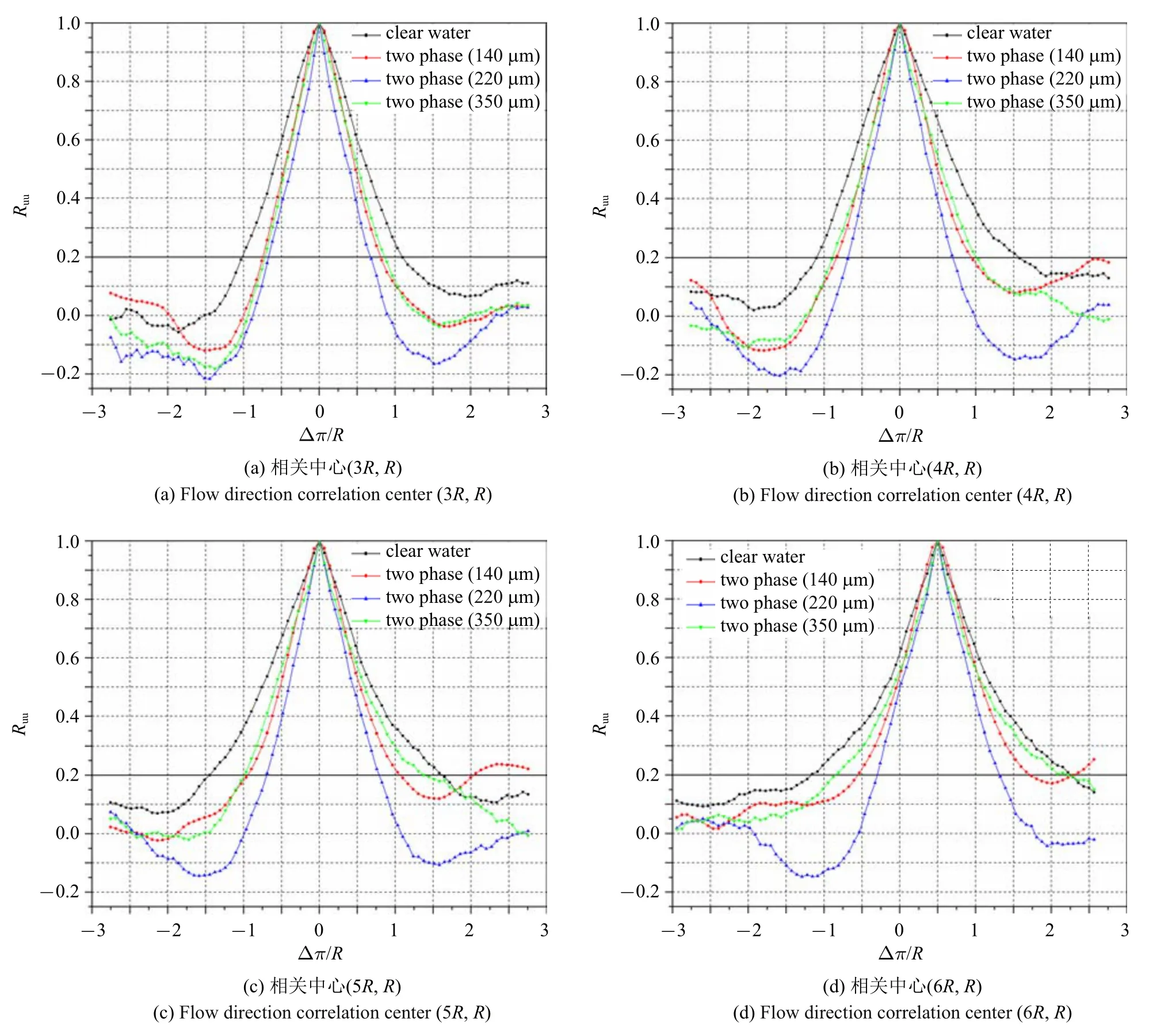
Jacobs[7]在1938 年最早对半球近尾迹和远尾迹的进行了研究.文献[8-11] 在边界层转捩与失稳的实验研究中,研究半球尾迹结构时发现尾迹结构中存在与光滑平板边界层中类似Theodorsen[12]提出的发卡涡结构.在边界层中半球尾迹结构演化的研究中,早期较为经典的是Acarlar 等[13]采用热膜风速法、氢气泡法和染料注入法对层流边界层内半球的涡旋脱落进行的研究,在雷诺数(ReR=RU/υ) 为120 图1 半球脱落发卡涡Fig.1 Shedding hairpin vortex from hemisphere Savory 和Toy[15]研究了浸入湍流边界层的半球的近尾迹结构,发现了类似于Acarlar 所描述的一个马蹄涡;Savory 和Toy 认为在近尾流中剪切层与周期性脱落的涡环存在相互作用,涡旋环的一半被描述为在半球顶部和通过剪切层传播,而另一半在半球迎风一侧的驻点或略高于驻点保持连接,因此认为它们与半球的上游面有着更强的联系.Kawanisi 等[16]通过研究半球尾迹的瞬时三维速度场,发现在半球尾迹结构中的大涡与低雷诺数时观察到的发夹涡相似,但在流向方向上没有观察到发夹涡的反向旋转腿,并且由于涡的拉伸在涡腿和涡头处产生较大的涡量.发夹涡头与壁面之间产生负展向涡量的二次结构.Tirtey 等[17]利用流动可视化和红外热像仪研究发现在半球尾迹的下游中存在持续多对流向涡,并诱导二次涡结构沿侧面传播.Ye 等[18]通过层析PIV拓扑了半球后的流动结构,发现湍流−非湍流界面上,普遍存在发卡涡对流和再生过程.Plesniak 等[19]将Acarlar 所发现的发夹涡称为SLH 涡,而且还存在剪切层卷起形成的静止的RA 涡.文献[20-21]利用直接数值模拟研究了平板边界层与孤立半球粗糙元之间的相互作用以及半球尾迹发夹涡的演化,结果显示发卡涡在半球的尾迹中形成交错的结构,在远离壁面过程中被边界层的剪切作用拉伸; 识别和研究了复杂涡旋拓扑演化过程可视化研究中几个关键特征.文献[22-24]的研究表明粗糙河床上存在半球形和球形障碍物会显著影响附近的平均流场、湍流输运特性和河床剪应力等,从而影响泥沙输运. 在液固两相流研究中,在平板的湍流边界层中的研究表明[25-26]小固体颗粒可以减弱近壁区的湍流强度,而大颗粒可以增强近壁区的湍流强度.文献[27-28]研究表明固体颗粒对流场的湍动能有明显的影响.文献[29-33]研究表明颗粒可以抑制相干结构,并促进猝发事件的产生. 根据现有研究发现,目前的液固两相流研究中绝大多数是基于光滑壁面假设的,粗糙壁面的液固两相流鲜有研究.固体颗粒对半球粗糙元的扰流结构的影响研究,为粗糙壁面液固两相研究奠定基础,对光滑壁面的液固两相研究有借鉴意义,也为理论研究和工程应用提供参考.本文利用粒子图像测速技术(PIV) 研究3 种固体颗粒对层流边界层中半球扰动的尾迹的影响,分析颗粒对半球后平均速度、湍流强度、回流区等宏观特性的影响.分别利用沿流向不同位置的流向脉动速度的二维空间相关系数和法向脉动速度的功率谱密度函数分析固体颗粒对尾迹结构演化过程及尾迹结构脱落频率的影响. 实验在河北工业大学PIV 流体力学实验室中型低速循环水槽中进行,实验装置如图2 所示.水槽实验段长为2500 mm,宽为500 mm,高为600 mm.平板长为2200 mm,宽为500 mm,厚为15 mm.平板水平放置在距水槽底部150 mm 处,并通过调节后缘板将平板表面沿流向的静压力梯度调节至接近于零,平板前端为8:1 椭圆修形,其背景湍流度小于0.8%实验过程中通过变频器调节水槽的自由来流速度为U=0.08 m/s,实验环境温度为20◦C,此时水的密度ρf=998 kg/m3;水的运动黏度υ=1.006 mm2/s,实验选取20 µm 的聚苯乙烯作为流场示踪剂,颗粒相选用大于Kolmogorov 尺度的直径为dp=140µm,220 µm,350 µm 的聚苯乙烯颗粒,颗粒密度ρp=1050 kg/m3.半球半径为12.5 mm,半球前缘与平板前缘距离为1400 mm.固体颗粒通过轴流泵以2 L/min从离液面深为5 mm、离半球水平距离为3 m 处注入配置的质量比为1:500(固体颗粒:水)的液固两相溶液. 图2 实验装置示意图Fig.2 Schematic diagram of experimental device 数据采集采用德国 Lavision 公司的 PIV 系统,激光器型号为LPY700,双脉冲激光最高频率为100 Hz,最大能量100 mJ,相机为4MX 相机(像素为2048×2048),最大采样频率为180 Hz.本实验的图像采集模式为双帧双曝,图像采集频率为70 Hz,曝光时间为满足两帧之间不少于5 个像素的位移,每种工况采集样本量为16 000 张,图像视野实际大小约为100 mm×100 mm(流向×法向).采集位置以半球中心为展向中心Z=0 位置.对于液固两相的原始图像通过高斯滤波后利用中值滤波提取固体颗粒,进而用两相图像减去固体颗粒图像得到示踪图像,如图3所示.固体颗粒的体积浓度使用固体颗粒的像素所占百分比表示,计算得到固体颗粒的面体积分数约为3.0×10−5.利用系统自带的Davis 系统对示踪图像采用互相关算法处理,查询窗口像素设置为32×32,重叠率为50%,得到的瞬时速度场有128×128 (流向×法向)个速度矢量. 图3 图像处理过程Fig.3 Image processing process 图4 平均速度剖面线Fig.4 Average velocity profile 图4 为半球后9 个流向位置的沿法向平均速度剖面线,速度剖面线随着距离的增加不断变化,随着流向位置增大速度剖面线之间的差异逐渐减小,如图所示在距离半球6R后平均速度剖面线几乎重合.颗粒对速度剖面线的影响随着流向距离的增大逐渐减小,从平均速度线的影响发现颗粒对平均流动影响较大的区域在距离半球后3R范围内.从速度剖面线发现在x=0.5R,R位置与其他位置不同,在一定高度区域存在负方向速度,表明在半球后存在一定区域的回流区. 图5 为流向0 ∼2R、法向0 ∼1.5R的平均速度云图,图中左下角的蓝色区域为回流区.回流区的流向大小随着固体颗粒粒径的增大而增大,法向高度几乎没有变化.平均流场反映了整体流动的模式,从流线图可以得到固体颗粒的存在对回流区附近的平均流动模式的影响,在清水工况下未形成大尺度涡旋结构,而在两相工况下流线弯曲闭合形成涡结构.从平均流动反映出固体颗粒的存在会改变回流区附近的瞬时流动结构促进涡结构的形成.另一方面,随着颗粒粒径的增大,流线的密集程度会先增大后减小,表明固体颗粒对涡结构的形成促进作用随着粒径的增大先增强后减弱. 图6 为半球后流向0 ∼8R、法向0 ∼4R的区域的综合湍流强度云图,其计算公式为 图5 回流区平均速度云图Fig.5 Average velocity nephogram in recirculation zone 图6 湍流强度云图Fig.6 Turbulent intensity nephogram 与清水工况相比,颗粒的运动导致了湍流强度的增大.从图6 可知在流向0 ∼2R、法向0 ∼R的区域内湍流强度随着流向距离增加湍流强度逐渐大.左下角的弧形区域为回流区,回流区内的湍流强度随着颗粒粒径的增大先增大后减小,在回流区右上方的弧三角的区域为涡结构存在的区域,在这区域内的湍流强度随着颗粒粒径的增大先增大后减小.在回流区后在流向2R∼8R、法向0 ∼R的区域内的湍流强度随着流向距离的增大逐渐减小,而在两相工况下的湍流强度随着粒径的增大而增大.法向高度1R以上的区域湍流强度变化较小. 由单相的半球尾迹结构的研究可知,半球诱导的尾迹结构脱落过程具有准周期性.利用功率谱密度函数对时间序列的信号处理分析颗粒的存在对尾迹结构脱落频率的影响. 在0 ∼2R的位置存在回流区,回流区后尾迹结构开始生成和演化,取法向高度y=R的几个流向位置的法向脉动的时间信号.如图7 所示是在不同流向位置的功率谱密度谱图.在功率谱密度函数图中当结构以某一频率出现时,功率谱密度值会以峰值出现.由于尾迹结构不断演化和生成,在功率谱分析时存在多个峰值,从图中发现不同流向位置会有同一频率出现,而这一频率代表了尾迹结构的脱落频率.清水工况下的脱落频率为1.5 Hz,140 µm,200 µm,350 µm 的工况下脱落频率分别为2.25 Hz,2.5 Hz,2.1 Hz.固体颗粒的存在增大了尾迹结构的脱落频率,但粒径对涡旋脱落频率影响呈非线性变化.根据斯特劳哈尔数提出基于半球尺寸、颗粒粒径、来流速度以及脱落频率的无量纲数S,其计算公式为 式中,dp为固体颗粒直径,f为脱落频率.表1 为两相工况下S值与f值.脱落频率f随着S值的增大先增大后减小.结合颗粒对于回流区附近流动及湍流强度的变化的影响,固体颗粒的存在促进了涡结构的形成,因此导致脱落频率的增大,两相工况下随着粒径的增大颗粒对涡旋形成促进作用会先增强后减弱,因此导致脱落频率随颗粒粒径非单调性变化. 半球扰动尾迹结构的空间尺度变化可以利用二维流向脉动空间相关系数进行分析,其计算表达式如下 式中,yyref为法向参考平面,r空间两点间的流向距,σ 表示流向脉动速度均方根.图8 为法向y=R时流向脉动流向相关系数随流向位置的关系图.4 种工况下随着相关系数从大到小变化趋势相同,为分析颗粒粒径对流向尺度的影响趋势,当以Ruu=0.2 为参考值时,流向相关尺度随着流向距离的增大而不断增大.对比清水和两相工况发现固体颗粒的存在使流向相关尺度减小,在两相工况下随着粒径的增大流向相关尺度先减小后增大,这种趋势与尾迹结构的脱落频率呈现一种负相关关系.因此颗粒的存在抑制了大尺度结构的脱落,抑制作用随着粒径的增大先逐渐增强后又逐渐减小.尾迹结构在沿流向生长和演化过程中存在不断旋转和拉伸运动,这种运动伴随着周期性速度加速和减速运动,从流向相关系数图中可以发现存在负相关峰,颗粒的存在促进了负相关峰系数的增大和负相关区域增大. 图7 功率谱密度函数图Fig.7 Power spectral density diagram 图7 功率谱密度函数图(续)Fig.7 Power spectral density diagram(continued) 表1 两相工况S 值与f 值Table 1 S value and f value of two-phase operating condition 图8 流向脉动速度流向相关沿流向位置分布Fig.8 Flow pulsation velocity and flow correlation distribution along flow direction 图9 和图10 所示相关中心分别为(4R,R)、(6R,R).与清水工况相比,固体颗粒的存在使尾迹结构的法向尺度减小,法向尺度的变化趋势与颗粒对于流向相关尺度的影响一致,并且随着流向距离的增大法向尺度不断增大.颗粒的存在也促进了负相关区域的增大,在相同空间位置负相关区域随着粒径的增大会先增大后减小,随着沿流向运动负相关区域会逐渐减小,如在140 µm 和350 µm 两种工况下都有明显的减小.在距离半球的4R的流向位置处由于受到回流区的影响以及涡结构生成的原因导致了负相关区域的增大,在两相工况下负相关区域及强度随着粒径增大先增大后减小,因此颗粒的存在促进了尾迹结构的周期性加速和减速运动,并且随着颗粒粒径的增大促进作用先增强后减弱.在沿流向运动过程中涡结构的周期性速度加速和减速运动逐渐减小,这表明尾迹尺度不断增大会减弱尾迹结构的周期性加速和减速运动. 本文利用粒子图像测速技术分别对清水和颗粒工况下的半球粗糙元后瞬时速度场进行测量,得到平均速度剖面、湍流强度等宏观统计量.并利用流向脉动速度相关系数分析尾迹结构尺度的变化.利用功率密度谱函数估算尾迹脱落频率.得到以下结论: 图9 相关中心为(4R,R)的二维流向脉动速度空间相关系数Fig.9 Spatial correlation coefficient of two-dimensional streamwise pulsating velocity with correlation center(4R,R) 图10 相关为(6R,R)的二维流向脉动速度空间相关系数Fig.10 Atial correlation coefficient of two-dimensional streamwise pulsating velocity with correlation center(6R,R) (1)与清水相比,颗粒的存在对平均速度剖面沿流向的变化趋势的影响较小; 两相工况下湍流强度增大,流向距离x=2R之前,湍流强度随着粒径增大先增大后减小,流向距离x=2R之后湍流强度随着粒径的增大而增大. (2)与清水相比,两相工况下回流区大小随着粒径增大逐渐增大.颗粒的存在改变了回流区附近的平均流动模式,促进了涡结构的形成,促进作用随着粒径的增大逐渐增强后逐渐减弱. (3)相关性分析表明,尾迹结构的流向相关尺度随着流向距离的增大逐渐增大,颗粒的存在使尾迹结构的流向相关尺度减小,两相工况下尾迹结构流向相关尺度随着粒径的增大先减小后增大.由负相关区域的分析发现颗粒促进了涡结构的周期性的速度的加速和减速运动,并且促进作用随着颗粒粒径的增大先增强后减弱. (4)与清水工况相比,两相工况下脱落频率增大,脱落频率随颗粒粒径的增大先增大后减小.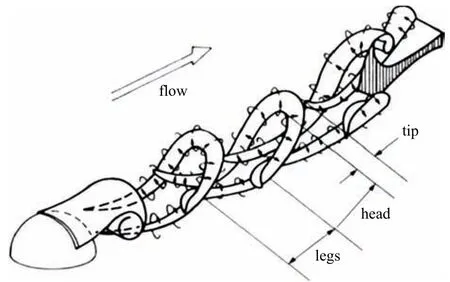
1 实验设备与参数
2 湍流宏观统计量
2.1 平均流动

2.2 湍流强度
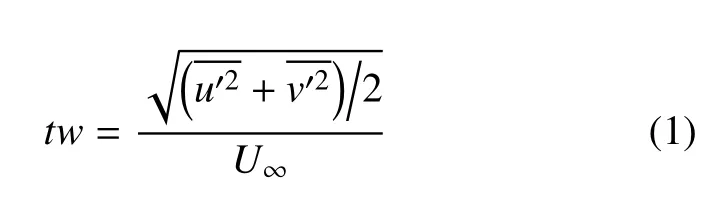
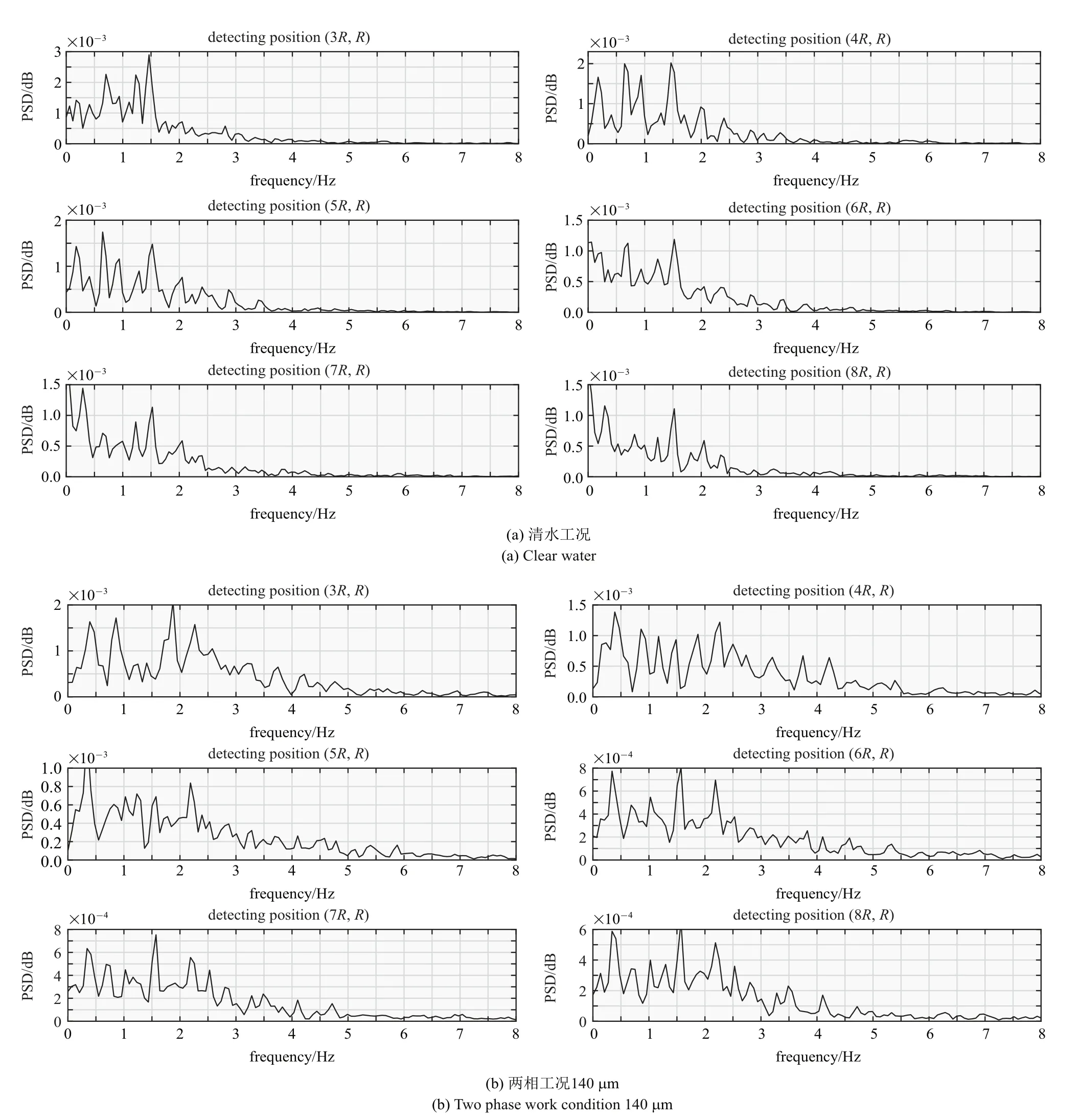
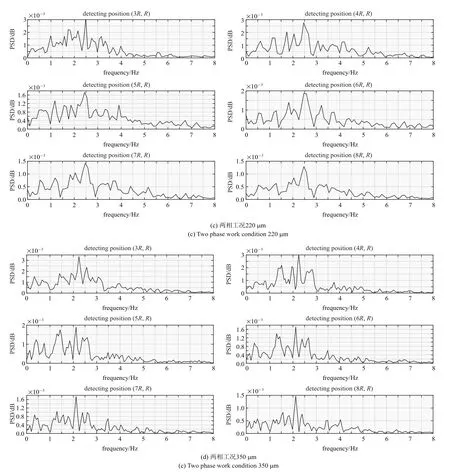
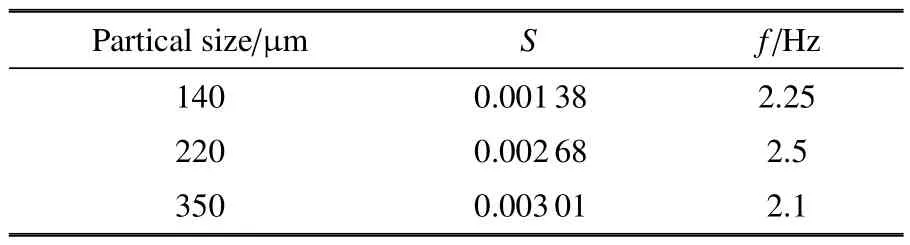
2.3 脱落频率

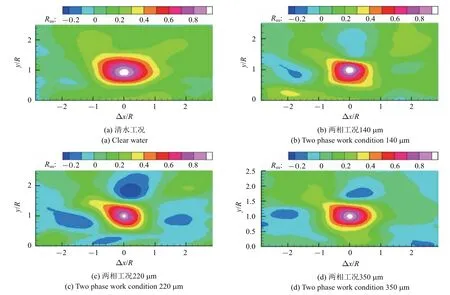
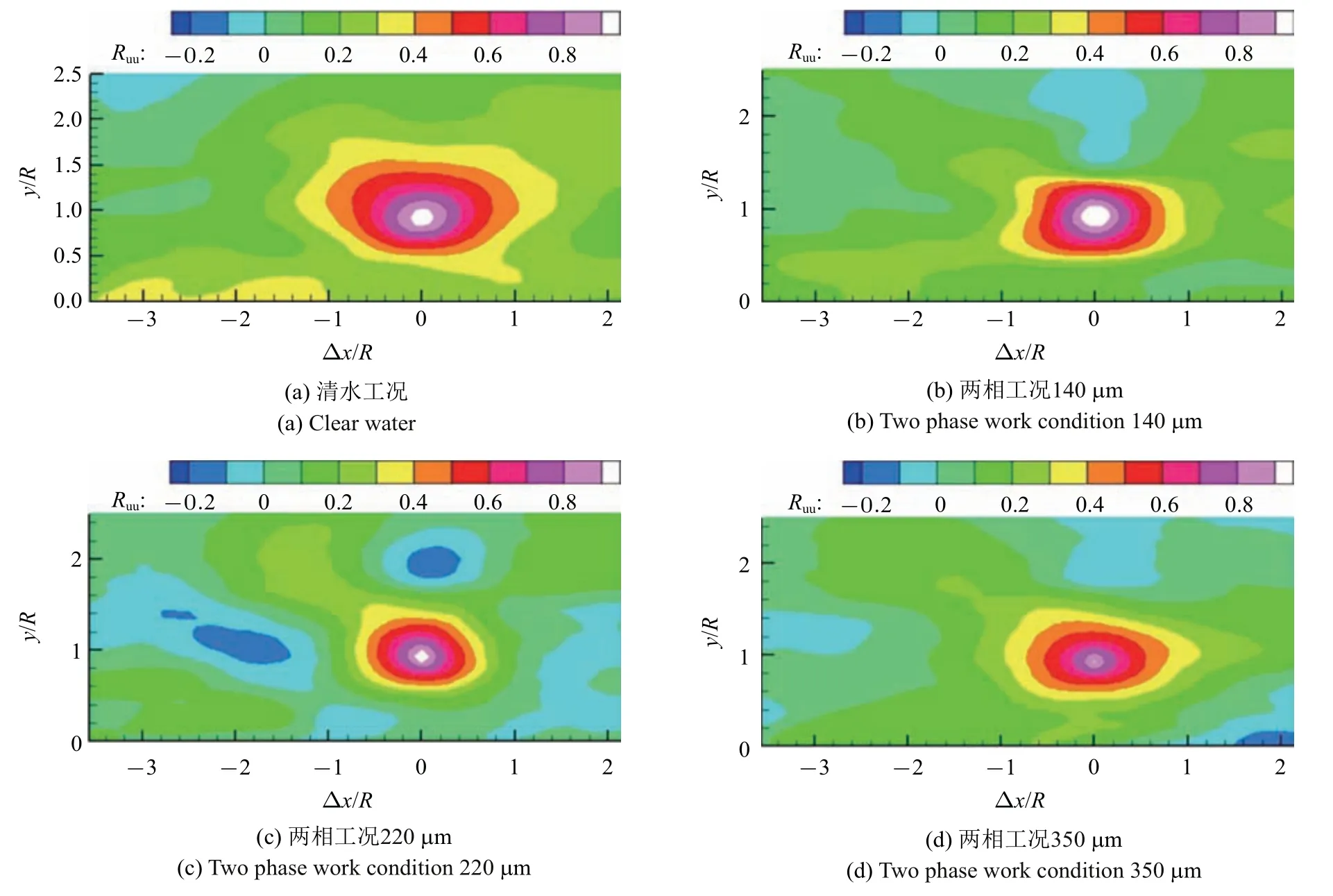
3 相关性分析
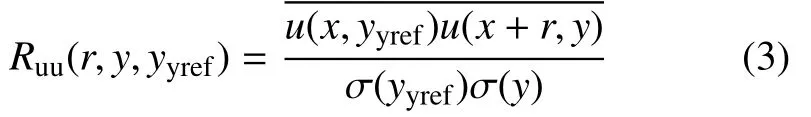
4 结论