基于变量加权统计分析的多微小故障诊断

闫治宇

（黄河水利职业技术学院 河南省开封市 475000）

1 引言

随着信息技术的进步，现代大规模、高复杂度的工业系统对数字化的监控要求越来越高，及时检测和诊断故障位置就变得至关重要，特别是系统重要环节出现故障时，所带来的后果更加严重。文献[1-3]中给出一些针对故障明显的诊断效果较佳的方法，但是微小故障存在幅值小、征兆弱的特点，从而造成诊断难度大，有关研究成果还较少。

主元分析(principal component analysis, PCA)是基于数据驱动的的重要分支，该方法不需要建立精准的机理模型，只需对过程数据进行统计分析，文献[4]研究得出系统微小故障不容易被检测，同时一般存在传递性，传统PCA方法不能及时检测故障。为解决这类问题文献[4-7]中给出从不同角度改进传统PCA算法，以达到对微小故障的诊断效果。但现有的关于PCA的微小故障诊断方法，在量纲相同的情况下，或是平等的对待系统所有变量；或假定是单变量发生故障。

为此，本文提出根据不同变量重要程度，赋予不同的权值，实现重要变量对微小故障的敏感度，以达到检测微小故障的目的；同时再利用故障特征子空间的相似性实现多微小故障诊断[8]。

2 离线建模

主元分析方法构建的主元模型为：

根据主元分析的几何意义，不同故障数据的特征矩阵是不相同的[10-11]，可用特征矩阵之间的相似度进行故障诊断[8]。因此，利用PCA方法提取历史故障数据的特征矩阵，并假设共有p种故障模式，第j种故障模式记作fj(j=1,2,…,p)，因此发生不同故障所对应的特征矩阵为。

3 在线过程监控

3.1 故障检测

设x(k)为k时刻传感器所采样的变量数据。

为提高重要变量对微小故障的敏感度，依据传感器所测变量的影响程度对在线数据的各变量赋予不同的权值W，加权后的数据矩阵如式（2）所示：

根据文献[9]计算加权数据的SPE统计量如式：

然后，通过SPE统计量是否超过阈值 来检测是否发生故障。

3.2 故障诊断

当故障出现时，用PCA方法处理当前过程数据，提取当前数据的特征矩阵然后，根据式（4）计算的相似度。

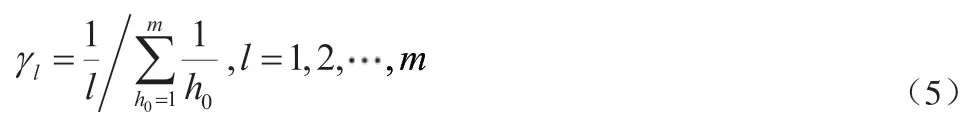
式（5）表示两个矩阵在m个特征方向上夹角余弦值的加权和，由于所以因此，两个矩阵的相似度越高即为式（5）的值越接近于1，进而实现故障类型的诊断[11]。

3.3 权值的选取

根据系统信号分析前后能量保持守恒的准则，结合系统先验信息对各变量重要程度的判断，可假定大致的比重因子[10]，如式（6）：

令：

因此，可根据式（8）所遵守的能量守恒得出待定因子α。

从而

由上述算法可得加权矩阵W：

权重因子wi反映着第i个变量在整个系统的重要程。

4 仿真实验

表1：两变量故障诊断表

图1：传统SPE检测图

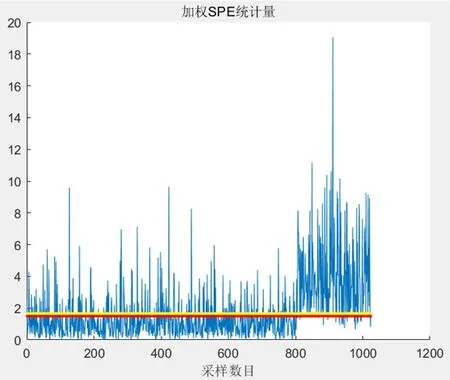
图2：加权SPE检测图

图1、图2为在801时刻当变量3、4同时加0.8倍变量方差恒值故障时，传统SPE统计量明显没有加权SPE统计量对微小故障的敏感性高，由此可见加权SPE对微小故障检测更敏感。

根据图1、图2所检测到的故障，可根据式（4）利用特征矩阵相似法进行故障诊断[8]，故障诊断结果如表1所示，其中诊断阈值τ=0.95。

由表1可以看出，只有变量3,4同时发生故障的矩阵相似度超过了诊断阈值，由此可以判断是变量3,4同时出现故障，这与所给变量加故障的情况相吻合，因此在检测到故障发生时，可利用特征矩阵相似法进行多微小故障诊断。

5 小结

在依据变量加权的基础上，引入特征矩阵相似度法，在提高了重要变量对微小故障的敏感度，增强故障诊断效果的同时，也解决了当多微小故障发生时，无法辨别的情况；具体做法为当检测到系统出现故障预警时，根据不同故障模式对应的特征子空间矩阵不同，进而利用特征空间矩阵的相似性来进行多微小故障诊断，实验结果说明了本方法的理论意义和实际有效性。