数学教学发展学生思维能力的路径思考
2020-06-09曾莲秀
曾莲秀
【摘 要】数学教学不仅是为了传授数学知识,更是为了利用数学知识这个载体来发展学生的思维能力,优化思维品质,培养学生的创新精神。教师可以在思维专练中、教学活动中、实物操作中、学业检测中发展学生的思维能力。
【关键词】教学;策略;思维训练
数学是思维的体操,发展思维能力是数学教学义不容辞的任务。郑毓信教授在《数学核心素养之我见》中指出:“将思维的发展看成数学核心素养的基本含义已越来越成为大家的共识。”学生理解数学知识并加以掌握是数学学科核心素养形成与发展的体现,它表现为学生从数学的角度,通过有条理地观察、分析、论证并解决相关问题。因此,数学教学应教会学生从数学的视角进行思考,这比教数学知识更重要,更有意义。
一、思维训练题改善思维品质
思维训练题往往比较有趣,富有启发性和挑战性,学生乐于探讨。有效利用数学思维训练题可以改善学生的思维品质。
如有这样一题:池塘里的浮萍生长面积每天扩大1倍,10天布满整个池塘,那么经过多少天浮萍长到池塘的一半?学生或一筹莫展或陷入繁杂计算,教师通过组织交流反馈,让学生感受到用逆向思考的方式能轻松破解此题,由此发散思维,感受逆向思维的出奇制胜。
又如这样一题:一张长方形纸,剪一刀剪掉一个角,还剩几个角?通过操作、交流、启发,可训练学生思维的广阔性。
二、教学活动常激发思维碰撞
学生思维能力的培养要落实到数学教学的每一节课中,除了单独开设的数学思维训练课之外,每道例题所呈现的“思考”过程,都能在培养学生数学思维方面发挥功能,都会影响学生思维能力的发展以及思维方式和思维习惯的养成。
如教学“面积”一课,教师在总结面积概念时提出:同学们发现物体表面和图形的大小就是它们的面积。那么,课本上是怎么说的呢?阅读课本,想想哪些地方和我们说的不一样,怎样说更准确。
生(阅读后指出):我们用的是“和”,课本上用的是“或”。
师:一字之差,有不同的意义吗?
生:不一样!“和”是两个一起,“或”是两个中选一个。
生:我们说的是“图形”, 课本上指的是“封闭图形”。
(随后教师出示不封闭图形和封闭图形,使学生明确,只有封闭图形才有面积。)
教学中,教师要给学生提供辨析的机会和时间,学生就会进行思辨,就可能做出批判性思考和回答,从而培养起批判性思维。
此外,教师在课堂上还应实施有效追问,引导学生更加深入地进行思考,提升学生思维的深刻性。教师可以在学生认知冲突处追问,在学生思维浅表处追问,在出现可利用的错误处追问,在学生回答精彩处追问。如教师可以这样追问:这个问题你有什么想法?这个想法可行吗?为什么?再想想我们还可以怎么解决。哦,是吗?其他同学怎么看?顺着这个思路往下走,看看又会有什么发现。
又如,在复习课中引用“思维导图”,让学生将颜色、图像、符码、文字等诸多信息生动地汇聚到一张图上,使知识的储存、管理及应用更加系统化,从而提高思维的效率,增强思维的整体性、逻辑性。
三、实物操作打开思维空间
教育家苏霍姆林斯基说:“儿童的思维离不开动作,操作是智力的源泉,是思维的起点。”正可谓动手启迪心智,操作拓展思维,学生在实物操作中、在趣味游戏中能锻炼思维能力,培养思维品质,提升思维水平。
数学特级教师任勇说,玩益智器具是能启发思维的,由动感、情趣走向理性和自觉,走向器具背后的思维,是益智游戏的主旨。教师在益智器具的教学中不是直接训练操作技能,而要侧重对解决问题(器具破解)策略的研究,注重思维方式的指导,挖掘玩法背后蕴藏的规律,以训练思维、发展能力。
如“汉诺塔”教学,教师可引导学生操作、观察、比较、类推,寻找圆环移动的最少步数及隐含规律,体会倒推、转换、递归等数学思想,培养学生分析、归纳、推理的能力是本节益智器具课的教学目标。
益智器具也可与数学教材内容有机融合进行拓展教学,这样一方面能激发学生的学习兴趣,另一方面通过操作活动,能把知识的获得和思维的发展有机结合起来。
如“四巧板与图形面积”教学,这节综合实践课选用益智器具四巧板作为研究对象,将四巧板拼图与人教版五年级上册第六单元组合图形面积有机融合,创新设计图形面积拓展练习课。本课充分挖掘四巧板器具蕴含的组合图形面积知识和数学思想方法进行趣味教学,使学生进一步体会“转化”的数学思想,培养学生的空间想象力、识图分析能力,发展学生的创新思维,提高解决问题的实践能力。
四、学业检测关注思维能力
数学课程的目標不仅仅是让学生获得必要的数学知识和技能,更重要的是全面发展学生的能力。与此相适应,考试命题则应关注能力考查,即把综合能力的考查放在首位,特别是数学思维能力。它可以促使教师在平时教学中真正重视知识的形成过程,重视分析问题的思路和方法探讨,重视数学应用价值的体现。
如有这样一试题:一个长方形的面积是576平方米,已知长方形的宽是9米,现在将长方形的宽增加到54米,长不变,现在的长方形的面积是多少平方米?一看到求长方形面积,学生的思维定式中会想到利用长方形面积计算公式(S=ab)来计算,其实这里还可利用现在的长方形与先前的长方形面积之间的关系来计算,增强学生思维的灵活性和广阔性。
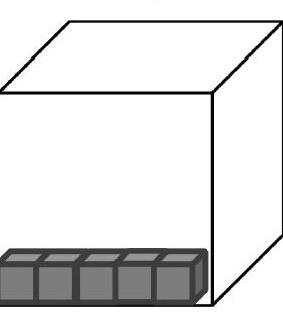
再如这样一试题:一个大正方体容器,靠着底面边长排放5个棱长为1厘米的小正方体后有空隙,但排不下6个(如右图),请估计大正方体的体积。要求写出分析过程,分析必须足够清晰,尽量使人理解你的思考过程。该题的特点是通过学生观察、分析、估算、表述,培养学生的空间观念、想象能力以及逻辑推理能力。
总之,培养学生思维能力的方法多种多样,要发展学生的思维能力,教师要注重构建益智课堂,关注思维素养落实。只要教师善于启发、引导、点拨,善于利用各种手段各种资源,持之以恒,为思维而教,就必定会有所成效。
(江西省抚州市实验学校 344000)