中美小学数学教材“两位数乘两位数”的比较研究

胡丹

【摘   要】“两位数乘两位数”是多位数乘法的关键课例。通过对中国人教版《数学》和美国My Math教材在这一内容的编写依据、内容编排等方面的比较研究，教师能更深刻地挖掘教材内涵，促进教学。在此基础上提出了三个可行性教学建议：实践操作具体化、计算方法多样化、几何直观可视化，以促进学生的数学思考更深入、数学思维更开放、数学观察更敏锐，从而提高学生的数学素养。

【关键词】两位数乘两位数;人教版; My Math

教材對数学教学活动的开展有着深刻的指导意义，它是教学的主要资源，是教与学的重要凭借。教师只有认真研读教材，准确理解教材的编写意图，寻找课程标准与教材的连接点，才能有效地开展教育教学活动。“两位数乘两位数”是小学数学计算教学的核心内容，是后续学习多位数乘法的重要基础。笔者基于“两位数乘两位数”这一内容，选取中国的人教版《数学》（以下简称人教版）和美国的My  Math（以下简称MM版）进行比较研究，以期为教材编者和小学数学教育工作者提供参考，从而促进教学，提升学生的数学素养。

一、两版教材编写依据的比较

人教版教材的编写依据是《义务教育数学课程标准（2011年版）》（以下简称中国课标）。中国课标中关于“两位数乘两位数”的内容是这样描述的：“能口算一位数乘两位数，能计算一位数乘三位数、两位数乘两位数的乘法。”MM版教材的编写依据是Common Core State Standards For Mathematics（以下简称CCSS课标）。CCSS课标中关于“两位数乘两位数”的内容是这样描述的：“用基于位值和运算性质的策略来计算最多四位数的整数乘一位数的整数、两个两位数相乘;使用方程式、矩形阵列或面积模型说明和解释计算。”两版课程标准对两位数乘两位数内容的要求有异同。

相同之处是两版课程标准对算法的要求基本相同。运算能力是数学学科的核心素养之一，是发展其他数学素养的重要基石。两版课程标准都要求学生能计算一位数乘多位数、两位数乘两位数的乘法，只是中国课标要求计算的是一位数乘三位数，而CCSS课标要求的是一位数乘最多四位数的整数。一位数乘三位数和一位数乘四位数的计算方法是一样的，所以两版课程标准对这一算法的掌握程度基本是一致的。

不同之处是两版课程标准对口算要求以及算理要求存在差异。能正确、合理、简捷地进行口算，体现了学生良好的数学素养。中国课标中提到“能口算一位数乘两位数”，表明中国数学教育界对学生口算能力的重视，而CCSS课标中却没有类似的相关要求出现。另外，培养运算能力，首先要让学生明白为什么这样算，即要让学生理解算理。CCSS课标中提到“用基于位值和运算性质的策略来计算”“使用方程式、矩形阵列或面积模型说明和解释计算”，可见CCSS课标明确要求通过多个途径帮助学生理解算理，而中国课标在这方面没有详细的陈述。

二、两版教材在内容编排上的比较

两版教材都是以图文并茂的形式呈现教学内容，并以儿童的视角为切入点，配以常见的生活场景的。但在具体内容的编排上两版教材还是存在差异，具体从以下三方面进行比较。

（一）知识准备的比较

在学习“两位数乘两位数笔算乘法”前，两版教材在这一单元中的知识准备内容罗列如下表。

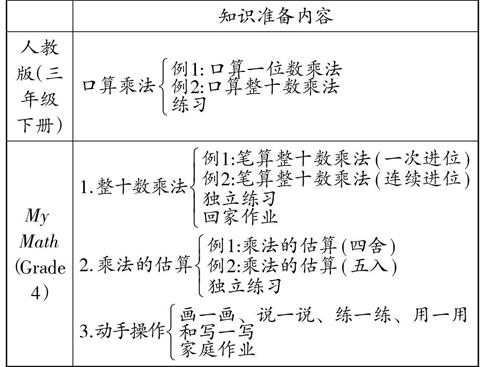
[ 知识准备内容 人教版（三年级下册） 口算乘法[例1： 口算一位数乘法例2：口算整十数乘法练习] My Math（Grade 4） 1.整十数乘法[例1：笔算整十数乘法（一次进位）例2：笔算整十数乘法（连续进位）独立练习回家作业]

2.乘法的估算[例1：乘法的估算（四舍）例2：乘法的估算（五入）独立练习]

3.动手操作[画一画、说一说、练一练、用一用和写一写家庭作业] ]

由上表可以发现，MM版教材在重点内容“两位数乘两位数笔算乘法”学习前，对知识的准备要更充分些，主要体现在动手操作这一内容上。采用画一画、说一说、练一练、用一用、写一写的方式，学生能理解并掌握通过面积模型把两位数乘两位数转化为已经学过的一位数乘整十数和一位数乘两位数的知识，为后续学习两位数乘两位数的笔算做铺垫。

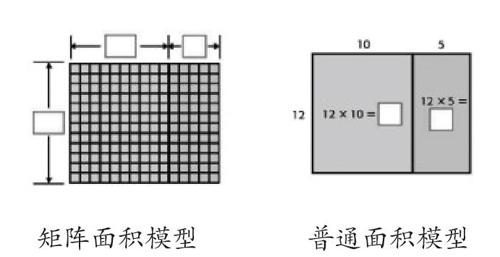
画一画，是先让学生在矩阵面积模型中找到12×15，接着通过把因数15分成10和5，并在矩阵面积模型中标注每个部分，再在简化后的面积模型中找到12×10和12×5，并计算出结果。而且在画一画之前，还让学生回顾了如何利用乘法分配律求出两位数乘一位数的乘积并用面积模型表征，可见对于利用面积模型来表征乘法算式，学生是有基础的。

说一说，是让学生分别说说如何利用乘法分配律求12×18和14×17，也就是通过“一数拆和”的方法来求两位数乘两位数的积。

练一练，是让学生画一个面积模型，然后利用乘法分配律在面积模型中找到每个部分的乘积。在第一题36×24中，作了面积模型表征的示范，而且练习的乘法算式有涉及连续进位的47×19，以及因数比较特殊的52×11，46×22。

用一用，是先出示需要解决的问题，然后让学生根据面积模型写出乘法算式并求出乘积。最后让学生改错，改正错误使用面积模型计算的情况。

写一写，是让学生解释为什么乘法分配律适用于两位数乘两位数。

以上五个实践活动为两位数乘两位数的笔算教学奠定了较为扎实的基础。

（二）算理理解的比较

两版教材都通过数形结合的表征方法来帮助学生理解算理，但在呈现的形式上又各有不同。

人教版教材呈现的表征方式比较丰富，有实物图、学具图、点子图，运用这三类图循序渐进地帮助学生理解算理。具体样例如下所示。

可见，人教版教材在几何直观的呈现上形式更多样，而MM版教材则相对比较单一。

（三）算法掌握的比较

人教版教材在两位数乘两位数的算法上一共出示了三种算法，分别是：“一数拆积”转换、“一数拆和”转换和竖式计算。下面是三种算法的样例。

竖式计算方法

MM版教材在算法上共呈现了四种算法，分别是：“一数拆积”转换、“一数拆和”转换、“两数拆和”转换和竖式计算。以下是四种算法的样例。

“两数拆和”转换方法

[另一种方法是使用纸和铅笔

竖式计算方法

MM版教材在算法种类的呈现上多了一种“两数拆和”的方法。这种方法对于四年级学生来说是比较难理解的，所以教材只是借助面积模型呈现，最后200+40+70+14这一步骤，省略了中间27×12转换为（20+7）×（10+2）=20×10+20×2+7×10+7×2的过程。可见，这一方法呈现的目的是引出与之对应的面积模型，让学生会运用这个模型来计算两位数乘两位数。所以在算法种类的呈现上，MM版教材借助面积模型呈现得更多更深。

但在学习“两位数乘两位数笔算乘法”时，人教版教材第一课时的算法呈现更多样，把三种算法都加以呈现。而MM版教材只有“两数拆和”和竖式计算两种方法。

三、思考与建议

通过两版教材的对比，我们可以发现有很多地方值得思考。

（一）实践操作具体化，让学生的数学思考更深入

两版教材最大的区别就是实践操作环节。人教版教材把实践操作渗透在每个课时中，相对比较隐晦。而MM版教材则是独立成一个课时，给出了更充足的时间和空间，让学生来实践操作。

在教学“两位数乘两位数”前，笔者曾对本校三年级两个班的学生做过前测，发现学生的学习起点普遍较高，近90%的学生能正确计算12×14，12×24两道题，有50%的学生会用两种及以上的方法来计算，但能借助点子图来表示计算过程的学生比例却不到20%。可见，很多学生会算，但不能很好地表示出为什么可以这么算。

因此，笔者建议教材编写者在编写“两位数乘两位数”这一单元时，可在教材中留出具体实践操作的课时，让学生有足够的机会和时间来探索两位数乘两位数算法的“数学化”过程，从而生发自己的数学体会，让数学思考力通过实践操作不断生长，最终能更深入地进行数学探究活动，提高数学素养。同时也让教师在教学时能明确实践操作的重要性，并在教学中更好地加以体现和实施。

（二）计算方法多样化，让学生的数学思维更开放

在“两位数乘两位数”这一单元中，两版教材都体现了算法的多样化。特別是人教版教材，在笔算乘法中同时出示了三种算法，这三种算法之间又都有联系。这不仅激发了学生的个性化学习，更让学生在探索和展示自己算法的过程中，体会到了数学学习的快乐。

因此，教师在教学“两位数乘两位数”时要体现算法的多样化，让学生不断地去思考“能不能算”“怎样算更好”。这样不仅能让学生掌握数学知识，更能让学生掌握数学思想，学会运用数学思维，最终让数学能力得到更好的发展。

（三）几何直观可视化，让学生的数学观察更敏锐

在帮助学生理解算理时，两版教材都借助了数形结合的方法。人教版教材的实物图、学具图、点子图，MM版教材的矩形阵列、面积模型，都用直观的形式描述了乘法运算的抽象过程，在形象思维和抽象思维之间构架桥梁，让思考过程可视化，让学生形成敏锐的观察力。

因此，笔者建议教师在教学时可利用实物图、点子图、面积模型等手段，让计算过程和思考过程更直观，让学生能在形象与抽象之间观察到共性，最终理解算法。

综上所述，通过对中美教材的比较，梳理异同，能让教师更深刻地挖掘教材的内涵，为更有效地开展教育教学活动，提升学生的数学素养奠定实践基础。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012：16-17.

[2]Initiative CCSS. Common Core State Standards for Mathematics[J].common core state standards initiative， 2010（4）：28-29.

[3]卢江，杨刚.义务教育教科书·数学（三年级下册）[M].北京：人民教育出版社，2013：41-53.

[4]McGraw Education.McGraw-Hill My Math（Grade 4）[M].The McGraw-Hill Companies，2013：295-343.

（浙江省杭州市江南实验学校   310052）