多层热防护服最优设计

孙若馨

【摘  要】论文运用数学的方法研究热防护服装并确定其最优厚度。首先建立热传导模型，并利用有限差分方法得到热传导方程的离散格式，之后根据热源温度和最内层的人体平均温度及服装材料的参数值，计算出各层初始条件。之后，利用MATLAB编程及热传导方程的离散格式得到各层的温度分布。最后，利用二分法，得到热防护服的最优厚度。

【Abstract】This paper uses mathematical method to study the thermal protective clothing and determine its optimal thickness. Firstly， the heat conduction model is established， and the discrete format of the heat conduction equation is obtained by finite difference method. Then， the initial conditions of each layer are calculated according to the heat source temperature and the average temperature of the innermost layer of human body and the parameters of the clothing material. Then， the temperature distribution of each layer is obtained by MATLAB programming and the discrete format of the heat conduction equation. Finally， the optimal thickness of thermal protective clothing is obtained by dichotomy.

【关键词】热传导模型;有限差分法;MATLAB软件;二分法

【Keywords】 heat conduction model; finite difference method; MATLAB software; dichotomy

【中图分类号】TS941.73                               【文献标志码】A                                   【文章编号】1673-1069（2020）02-0187-05

1 引言

服装是人与周围环境的中间体，起着第二层皮肤的作用。随着各种各样行业面临的环境越来越复杂，人类对具有各种特殊性能服装的要求也越来越高。目前，热防护服是一种应用最为广泛的特种防护服装。

热防护服是对在高温或者超高温环境下的工作人员进行保护的工具，是防止中暑、烧伤和灼伤等危害，避免热源对人体造成伤害的保护性服装，因此，其必须具备拒液性、阻燃性、遇热时能够保持服装的完整性、穿着舒适性以及燃烧时无熔滴产生等必要性能。热防护服的防护原理[1]是降低热转移速度，使得外界的高热缓慢而少量地转移至皮肤[2]。热防护服的质量要求和使用方法等内容，关系到热防护服装的防护作用和从业人员的工作质量和效率[3]。运用数学的方法研究热防护服，是在揭示热防护织物内部的热传递规律[4]。

自20世纪50年代开始，人类就已经进行了热防护服方面的研究，在防护服的隔热性能、舒适性能方面取得了一系列成果。起初，国内外研究者主要研究单层热防护服，考虑环境中火焰的热辐射、织物材料的物理学性质以及织物与人体皮肤层之间的空气层厚度等因素对防护性能的影响[5]。Torvi[6]提出热防护服外层织物的热传递模型;朱方龙[7]研究了曲面下的热传递过程;在ASTMD4108的实验装置基础上，Sawcyn[8]进一步研究了防护服和空气层的热传递模型;Ghazy[9]在防护服-空气层-皮肤组成的系统中建立了单层织物的热传递模型。在单层热防护服模型的基础上，许多学者又研究了多层热防护服传递模型。Mell[10]提出了多层织物层与层之间的热传递模型。该模型与Torvi的模型相似，属于Torvi模型处理多层织物材料热传递的延伸;Mercer[11]研究了相变材料的多层防护服的热传递模型及其材料对热传递的影响。

目前来看，很多研究集中在防护性能测试、建立热传递模型、防护服装舒适性评价等方面，对防护服最优设计的理论研究方面尚有欠缺。本文根据经典的热传递模型，提出了高温环境下热防护服的热传递模型，来描述高温环境下热防护服的热传递规律，之后对所提出的模型，给出了显示有限差分方法[12]的数值模拟，并结合二分法[13]求出特定条件下的热防护服的最优厚度，使防护服达到制作成本最低、舒适性最好、隔热性能最优的效果。

2 模型构建

2.1 问题描述

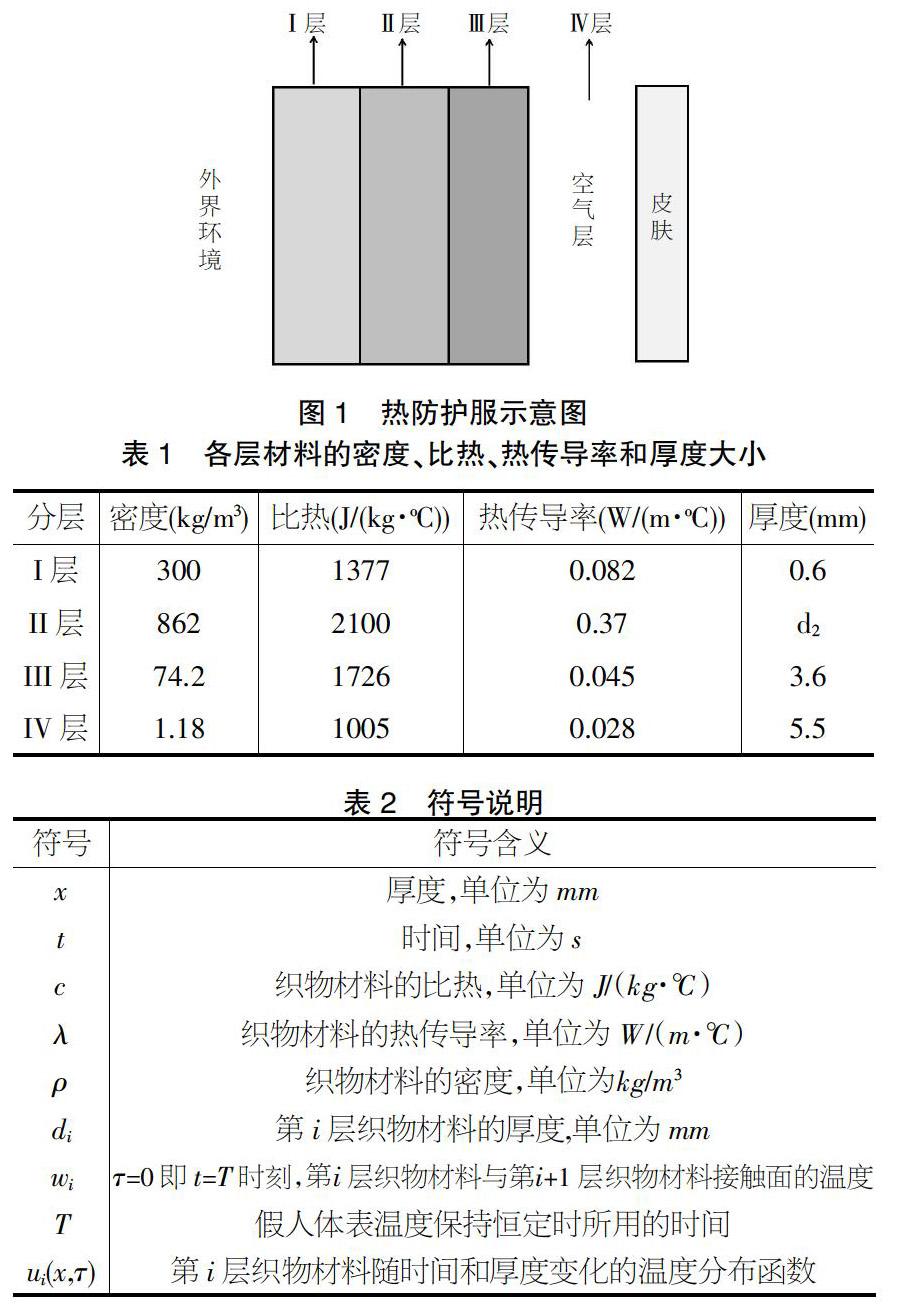
热防护服由3层织物材料构成，设与外界环境接触层为Ⅰ层，从外向里依次为Ⅰ、Ⅱ、Ⅲ层，Ⅲ层与皮肤之间的空隙层设为Ⅳ层（见图1）。以体表温度为37℃的穿热防护服的假人为實验材料，在外界温度恒为65℃，Ⅳ层厚度为5.5mm的条件下，设计出Ⅱ层的最优厚度，使其工作1h时，皮肤外侧的温度不大于47℃，并且大于44℃的时间不大于5min。表1给出了每层材料的密度、比热、热传导率和厚度大小。文中用到的符号说明如表2所示。

2.2 模型假设

①防护服的材料是各向同性的。

②热量沿垂直皮肤的方向传递。

③热传导过程中没有湿传递（汗液、水汽的影响）。

④防护服层与层之间接触良好，结合面上温度处处相等。

2.3 模型构建

高温环境下，假人穿着热防护服，形成“高温环境-服装-人体”导热系统。通过查阅资料，由傅里叶定律和能量守恒定理推导出防护服的三维热传导微分方程模型：

3 模型的求解

下文将应用显式有限差分法和二分法对模型进行求解。首先在第Ⅱ层织物材料厚度为最小值0.6mm的情况下，以第Ⅰ层织物材料为起始层，逐层推导出每一层织物材料温度分布的初始条件和边界条件，并结合热传导方程的离散格式，通过MATLAB编程得出每一层的温度分布情况，然后观察人体表面的温度分布情况。接下来选取第Ⅱ层织物材料的厚度为最大值25mm，在第Ⅱ层织物材料厚度为最大值的情况下，求得人体表面的温度分布并观察。然后利用二分法逐步选取第Ⅱ层的厚度，重复上述步骤，观察各厚度下人体表面的温度分布情况，最终选取最优厚度（即确保工作60min时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5min）。

3.1 初始条件和边界条件的确定

3.1.1 热传导方程的显式离散格式

3.1.3 边界条件及各层织物材料温度分布的确定（以d2=0.0006m为例）

令u1（x，）=65作为第Ⅰ层织物材料温度分布的边界条件、u1（x，0）=1196.6667x+64.2820作为第Ⅰ层织物材料温度分布的初始条件。根据热传导方程的离散格式（3）式，利用MATLAB编程求解，可得出第Ⅰ层织物材料的温度随时间和厚度变化的三维函数图像，即第Ⅰ层织物材料的温度分布，如图3所示。

令第Ⅰ层织物材料求得的在边界x=d1的温度分布作为第Ⅱ层织物材料温度分布的边界条件（见表3）、u2（x，0）=1196.5x+63.5641作为第Ⅱ层织物材料温度分布的初始条件。根据热传导方程的离散格式（3）式，利用MATLAB编程求解，可得出第Ⅱ层织物材料的温度随时间和厚度变化的三维函数图像，即第Ⅱ层织物材料的温度分布，如图4所示。

令第Ⅱ层织物材料求得的在边界x=d2的温度分布作为第Ⅲ层织物材料温度分布的边界条件（见表4）、u3（x，0）=2026.6667x+56.2681作为第Ⅲ层织物材料温度分布的初始条件。根据热传导方程的离散格式（3）式，利用MATLAB编程求解，可得出第Ⅲ层的温度随时间和厚度变化的三维函数图像，即第Ⅲ层织物材料的温度分布，如图5所示。

令第Ⅲ层织物材料求得的在边界x=d3的温度分布作为第Ⅳ层织物材料温度分布的边界条件（见表5）、u4（x，0）=3503.2909x+37作为第Ⅳ层织物材料温度分布的初始条件。根据热传导方程的离散格式（3）式，利用MATLAB编程求解，可得出第Ⅳ层织物材料的温度随时间和厚度变化的三维函数图像，即第Ⅳ层织物材料的温度分布，如图6所示。

观察假人体表面温度分布，即第Ⅳ层织物材料求得的在边界x=d4的温度分布，观察其是否满足要求：工作60min时，假人体表温度不超过47℃，且超过44℃的时间不超过5min。

3.2 利用二分法求解第Ⅱ层的最优厚度

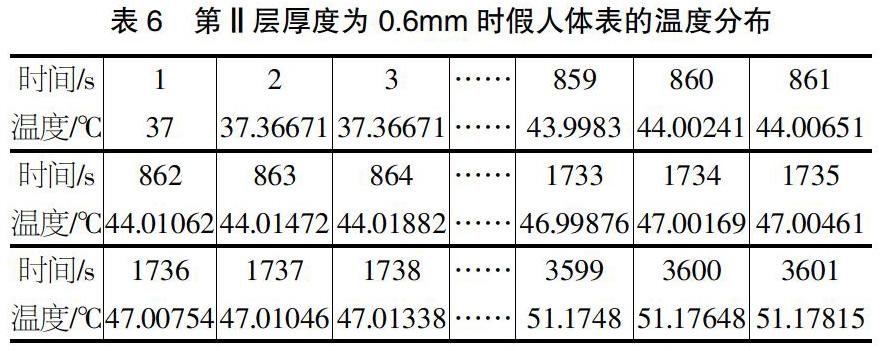
令d2=0.6mm，用上述的求解步骤，得到假人体表随时间变化的温度分布，由表6可以看出，在第860s即第14min 20s假人体表温度超过44℃，在第1734s即第28min 54s假人体表温度超过47℃，即假人体表温度超过44℃的时间不仅大于5min且假人体表温度超过了47℃，所以第Ⅱ层织物材料厚度为0.6mm时需要变厚。

令d2=25mm，用上述的求解步骤，得到假人体表随时间变化的温度分布，由表7可以看出，假人体表温度全程都不会超过44℃，所以第Ⅱ层织物材料厚度为25mm时需要变薄。

利用二分法取d2=12.8mm，用上述的求解步骤，得到假人体表随时间变化的温度分布，由表8可以看出，假人体表温度全程都不会超过44℃，所以第Ⅱ层织物材料厚度为12.8mm时需要变薄。

利用二分法取d2=9.75mm，用上述的求解步骤，得到人体表面随时间变化的温度分布，由表9可以看出，假人体表温度在第2851s即第47min 31s超过44℃，超过44℃的时间大于5min，所以第Ⅱ层织物材料厚度为9.75mm时需要变厚。

利用二分法取d2=11.275mm，用上述的求解步骤，得到假人体表随时间变化的温度分布，由表10可以看出，在3223s即第53min 43s超过44℃，超过44℃的时间大于5min，所以第Ⅱ层织物材料厚度为11.275mm时需要变厚。

利用二分法取d2=12.0375mm，用上述的求解步骤，得到假人体表随时间变化的温度分布，由表11可以看出，假人体表温度全程都不超过44℃，所以第Ⅱ层织物材料厚度为12.0375mm时需要变薄。

利用二分法取d2=11.3227mm，用上述的求解步骤，得到假人体表随时间变化的温度分布，由表12可以看出，在假人体表温度在第3363s即第56min 03s超过44℃，超过44℃的时间小于5min，所以第Ⅱ层织物材料厚度为11.3227mm时需要变薄。

从而得到，第Ⅱ层的最优厚度应介于11.275mm与11.3227mm之间，我们定为11.3227mm。

4 结果分析

在第Ⅱ层织物材料厚度为0.6mm时，假人体表温度在第14min 20s就超过44℃，工作人员无法长时间在高温下工作，说明此时第Ⅱ层织物材料厚度过薄，热防护服隔热效果不好;在第Ⅱ层织物材料厚度为25mm时，符合要求，热防护服隔热效果好，但此时织物材料的厚度过厚，不仅导致了材料的浪费，而且导致热防护服体积、重量变大，不利于人员工作，因此，可以減小第Ⅱ层织物材料的厚度。利用二分法取不同的厚度发现，当第Ⅱ层的最优厚度介于11.275mm与11.3227mm之间时，热防护服既有很好的隔热效果，也保证了热防护服的轻薄，此时最利于工作人员在高温下工作，因而可以认为11.3227mm为第Ⅱ层织物材料的最优厚度。

5 结语

热防护服是高温条件下工作人员的必要保护工具，其防护服的性能影响着有关工作人员的安全，因此，研究多层热防护服的最优设计具有重大意义。本文基于热传导微分方程建立了防护服热传递模型，同时应用该模型预测了在不同的织物层厚度条件下温度的分布情况，并以此求出防护服的最优设计，为实际生活中的防护服的设计提供了理论依据。且本文中织物材料的厚度数据是人为设定的，各制造商或者其他厂家可以根据自身需要修改。但是，本文在研究过程中仅考虑到织物层和空气层的厚度对防护服性能的影响，没有考虑其他影响因素，还需要在将来的研究中继续深入。

【参考文献】

【1】华涛.热防护服热防护性能的分析与探讨[J].产业用纺织品，2002（08）：28-31.

【2】王来力.高性能防护服的发展现状与展望[J].中国个体防护装备，2009（3）：20-22.

【3】張燕.我国防护服装标准现状和标准体系框架构想[J].中国个体防护装备，2006（5）：37-39.

【4】潘斌.热防护服装热传递数学建模及参数决定反问题[D].浙江：浙江理工大学，2016.

【5】卢琳珍，徐定华，徐映红.应用三层热防护服热传递改进模型的皮肤烧伤度预测[J].纺织学报，2018（1）：111-118.

【6】David A. Torvi. Effects of Variations in Thermal Properties on the Performance of Flame Resistant Fabrics for Flash Fires[J]. Sage Publications，1998，68（11）.

【7】朱方龙.服装的热防护功能[M].北京：中国纺织出版社，2015.

【8】Sawcyn， Chris M J，Torvi， David A. Improving Heat Transfer Models of Air Gaps in Bench Top Tests of Thermal Protective Fabrics[J]. ProQuest，2009，79（7）.

【9】Ahmed Ghazy，Donald J. Bergstrom. Numerical Simulation of Heat Transfer in Firefighters' Protective Clothing with Multiple Air Gaps during Flash Fire Exposure[J]. Taylor & Francis Group，2012，61（8）.

【10】W.E. Mell and J.R. Lawson. A Heat Transfer Model for Fire Fighters Protective Clothing [J]. Fire Technology，2000，36（1）：39-68.

【11】Mercer G N ， Sidhu H S . Mathematical modelling of the effect of fire exposure on a new type of protective clothing[J]. Australian & New Zealand Industrial & Applied Mathematics Journal， 2007，49：289-305.

【12】张宝琳，申卫东.热传导方程有限差分区域分解算法的若干注记[J].数值计算与计算机应用，2002（02）：81-90.

【13】宋心茹.利用二分法求方程的近似解[J].备课参考，2013（12）：21-23，25.

【14】郑坤灿，陈莉荣，向峰伟.对一维稳态传热过程类电流求解方法的讨论[J].中国冶金教育，2012（6）：48-51.