基于多尺度的贝叶斯模型显著性检测

常 振，段先华，鲁文超，彭 媛

江苏科技大学 计算机学院，江苏 镇江212000

1 引言

显著性检测能够提取出图像中对人类视觉比较有吸引力的区域，是计算机视觉任务的关键步骤，被广泛应用于图像压缩[1]、图像分割[2]、物体检测[3]、图像检索[4]、对象识别[5]、图像分类[6]等领域，并取得显著成果。尽管显著性检测在计算机视觉任务中取得了巨大成功，但是显著性的定义依赖于多种因素，很难用一种方式把所有的检测线索有效地统一起来，因此准确的显著性检测仍是一个难题。

早期的显著性检测方法主要受视觉注意的感知研究启发，感知研究表明对比度是人类视觉注意系统中视觉注意力的主要因素，并由此出现了基于不同线索对比的显著性检测算法。受生物模型启发，Itti等人[7]采用颜色、亮度和对比度三个特征表示输入图像，并通过特征图标准化及线性组合得到最终显著图。Hou等人[8]将图像显著性计算引入到频域，其基本原则是抑制频繁出现的特征响应，同时对变化的特征保持敏感。Rahtu等人[9]提出一种基于贝叶斯理论的显著性检测模型。该模型应用滑动窗口将图像分成核心和边缘，通过比较核心和边缘特征计算每个像素显著值。

随着深入研究，出现了基于对比度的显著性检测算法。Liu 等人[10]使用局部区域和全局特征计算显著性。这些特征包括：多尺度对比、中心-周围直方图和颜色空间分布。通过条件随机向量场的学习将三个特征有效结合用于显著性区域的检测。由于仅通过局部对比，该算法更趋向于关注边缘周围的区域，导致出现“不一致突出显著区域”的问题。Achanta 等人[11]从频域角度出发，首次提出一种基于全局对比的显著区域检测算法。该算法首先对输入图像进行高斯低通滤波，然后将滤波后的图像中的每个像素值和整幅图像的平均像素值之间的欧几里德距离作为该像素的显著值。由于该算法对图像显著区域中的最显著部分有一定的抑制，导致得到的显著图与背景的对比不明显。基于此，Cheng 等人[12]提出基于全局对比度的显著性检测算法。该类算法充分考虑了图像的全局特征，能够更好地突出显著目标。但该算法对于复杂背景的图像或者多个目标图像检测效果较差。

近年来，一些研究者将背景信息引入显著性检测方法中。文献[13]提出的基于背景先验的显著性检测算法以各超像素到图像边界的测地线距离长短作为衡量显著性的标准，距离越短超像素作为背景的可能性越大。但是检测结果不理想，可能会把与边缘较近的显著区误判为背景，影响检测精度。Jian 等人[14]提出一种基于扩展随机游走（ERW）排序和背景种子的显著性检测模型，其中背景种子是基于似物性采样（object proposal）计算的。该模型通过有效结合图像纹理信息和全局结构以优化显著性图，能够较好地将显著区域和背景分离。Huang等人[15]将前景先验和背景先验进行融合以检测显著区域，首先利用被包围状态定位前景种子以计算前景显著图；然后从图像边界选择背景种子以计算背景显著图；最后，将前景和背景显著图融合得到显著图。但是该方法对于前背景对比度不明显的图像，易将背景噪声误认为显著区，从而影响检测结果。

基于贝叶斯模型的显著性检测算法[16]以中层和低层信息为基础，结合贝叶斯理论得到更加完整的显著图。但是该算法的检测区域中包含较多背景，检测效果较差。

针对上述问题，本文在贝叶斯模型的基础上进行改进，提出了一种结合图像背景先验和凸包先验的多尺度的显著性检测算法：（1）对原图进行超像素分割，将其分割成四种不同的尺度；（2）根据不同超像素数目获取相应的图像边界信息，计算每个超像素所包含的边界权重，排除前景区域，获取多尺度超像素的背景种子；（3）以背景种子为基础，根据图像中剩余超像素与背景种子之间的颜色和空间距离信息，计算背景先验图；（4）对原图进行颜色增强，利用Harris算子进行角点检测求得凸包区域，并结合分割完成的超像素计算凸包先验图；（5）将背景先验图和凸包先验图通过融合得到最终先验图，并由凸包区域和图像颜色直方图计算似然概率；（6）通过贝叶斯模型计算显著图，并对其优化得到最终显著图。本文算法流程图如图1所示。

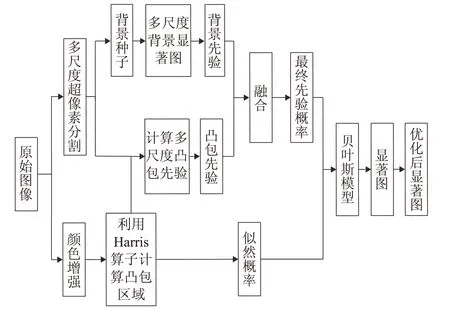
图1 算法流程图

2 多尺度贝叶斯模型算法

贝叶斯框架是一种通过先验概率和似然概率计算的模型。本文依据文献[17]提出的贝叶斯模型进行显著性检测，并依据该模型理论估计图像中每个像素x 的后验概率：

其中，p(sal|x)表示像素x 的显著性概率，p(sal)表示像素x 为显著性的先验概率，p(bx)表示像素x 为背景的先验概率，p(x|sal)和p(x|bx)表示像素的观察似然概率。

2.1 背景先验

由于图像边缘通常包含极少的显著目标和较多的背景区域，故可将图像边缘视为背景区域。为此，本节基于多尺度超像素查找背景种子，利用背景种子计算出多尺度超像素之间的空间与颜色距离，得到背景先验图。

图2 多尺度超像素对应显著图

本文将超像素作为最小处理单元，利用简单线性迭代聚类（SLIC）算法[18]将图像分割成KS 个超像素，继而通过边界概率（PB）[19]得到图像边界，并根据边界信息得到背景种子以及各个超像素的显著性，融合不同尺度超像素的显著图得到最终基于背景种子的显著图。具体算法描述如下：

（1）将原图分割成KS 个超像素，计算其平均颜色和空间位置分别表示为，其中k(k=1,2,…,KS)表示每个超像素对应的标签。

（2）根据PB计算图像边界，第k 个超像素的表示范围为：

其中，Bk表示第k 个超像素的边缘像素集合， ||Bk表示其基数，KPpb表示像素KP 的PB值。

（3）根据图像边界计算出每个超像素所包含权重，利用自适应灰度阈值[20]剔除前景区域，将边界中剩余的超像素作为背景种子，利用空间和颜色距离计算基于背景种子的超像素k 的显著性：

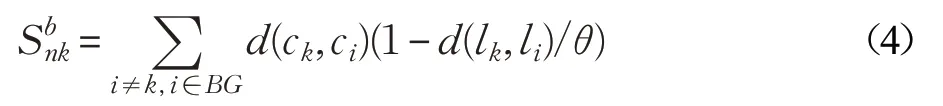
其中，n 为当前分割的超像素数目，BG 为背景种子集，li表示第i 个超像素的中心位置，ci表示CIELab平均颜色向量，d(ck,ci)和d(lk,li)分别表示第k 个超像素和第i个超像素之间的颜色欧式距离和空间距离。

（4）由公式（4）计算出超像素数目为100、200、300、400 的背景显著图，分别表示为、、、，并对其进行融合得到最终背景先验p(sal1)。

融合后的背景先验如图2（f）所示，和图2（g）相比背景噪声明显减少，显著区域更为明显。可以看出基于多尺度的背景先验方法能有效减少图像中显著区域的噪声和冗余，更加接近目标区域。

2.2 凸包计算

凸包通常是通过计算图像特征点得到的一个能够将所有特征点包含在内且面积最小的多边形。图像处理中常用的特征点检测方法有FAST 算子、SIFT 算子、SURF 算子和Harris 算子等。其中Harris 算子能够精确定位局部特征，计算量小且较为稳定，故本文基于Harris算子进行特征点检测。

由边界即是背景[21]可知，凸包内的为显著区域，凸包外的为背景区域。而直接采用Harris 算子得到的图像凸包可能会出现凸包内包含较多背景区域的情况，与实际情况有很大的差异，如图3所示。

图3 采用Harris角点检测形成的凸包示意图

基于此，本文通过颜色增强Harris 角点[22]计算凸包区域。具体操作如下：

（1）对输入图像进行颜色增强，提升前景和背景的对比度，增强后的效果图如图4（b）所示。

（2）对增强图采用Harris算子进行角点检测以获得凸包区域，如图4（c）所示。可以看出该凸包区域包含较少的背景区域，图4（d）为凸包对应的二值图。

图4 基于增强图的凸包区域

2.3 先验概率计算

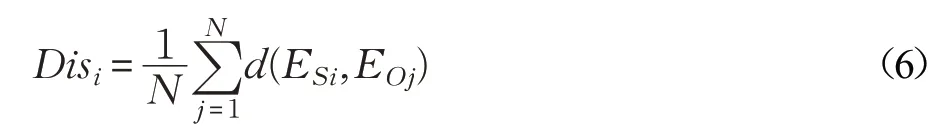
其中d(ESi,EOj)代表ESi和EOj之间的颜色距离。将与外簇具有最大颜色距离的内簇称为显著簇。基于此，计算出剩余超像素与显著簇中的超像素之间的颜色和空间距离，得到超像素的显著性。

设显著簇中的超像素个数为X(X ＜KS)，显著簇中的第x(x ∈(1,2,…,X))个超像素的显著性为Sx，则不同尺度超像素（n 为当前分割的超像素数目）的显著性为：

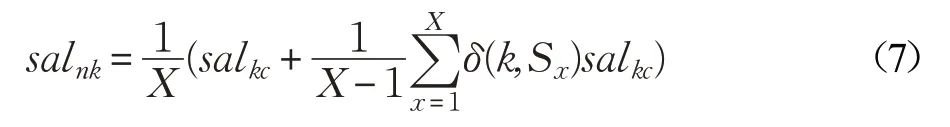
其中：

由公式（7）可计算出超像素为100、200、300、400 的先验概率，分别表示为sal100k、sal200k、sal300k、sal400k。根据公式（10）对这四个尺度的先验概率进行融合，得到基于凸包的先验图p(sal2)，如图5（b）所示。

图5 先验图

最后，将2.1 节中的背景先验p(sal1)和本节中的凸包先验p(sal2)两者取交集，由公式（11）计算出最终先验图。

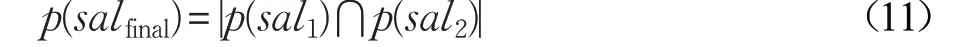
如图5所示，基于本文方法得到的先验图能够更好地去除背景噪声，提高先验概率的准确率。

2.4 观察似然性

利用常规的中心周围原理进行似然性计算会增加计算量，而利用凸包估算大致的显著区域能有效减少计算代价。对于包含特征点的凸包，只需计算显著区域中每个像素的显著性。

凸包将图像分割成两个不相交区域：凸包内区域S和凸包外区域O。由文献[23]可知，所有检测到的显著点都在区域S 中，而区域O 则偏向于背景。单个像素的显著性不仅取决于它与凸包内区域S 的相似性，而且取决于与凸包外区域O 的差异。CIElab颜色不仅能够较好地反应物体色的心理感受效果，而且保存了像素的颜色和亮度信息。基于此，在CIElab空间中进行处理。

颜色空间的每个像素x 用[l(x),a(x),b(x)]表示，Ns和No分别表示区域S 和区域O 颜色直方图，Ns(f(x))(f ∈{l,a,b})和No(f(x))(f ∈{l,a,b})分别表示区域S 和区域O中颜色值f(x)在颜色直方图中的对应值。为了提高效率，认为CIELab颜色空间中的3个颜色通道l,a,b 是互不干扰，相互独立的。像素x 的似然概率为：

第3步：在软件Matlab 2012b中通过编程求得该预测方法的相对误差，并且与BP神经网络直接预测法的相对误差进行对比分析。

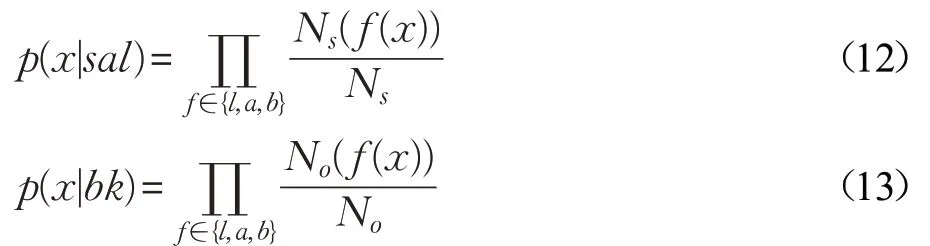
2.5 显著图以及优化

由2.3节和2.4节得到的先验概率和似然概率，通过贝叶斯公式得到显著图。将公式（11）～（13）代入公式（1）计算凸包内每个像素的显著性概率，得到显著图。如图6 所示，可以看出得到的显著图不平滑，存在块状效果。为此，本文采用文献[24]中的优化算法（公式（14））对图6（b）进行优化，得到最终显著图Sfinal。

其中，i、j 为像素坐标，W 和H 分别代表图像的宽和高，Savg为显著图Sp(i,j) 的平均显著值。优化后的显著图如图6（c）所示，和图6（b）相比，优化后的显著图与Ground-Truth非常接近，准确率明显提高。

图6 显著图及优化后的显著图

3 实验结果与分析

本文采用MatlabR2016b，计算机内存16 GB，处理器为Intel®Core™i7，主频为2.2 GHz 作为实验环境。为了验证本文算法的准确性和有效性，将本文算法与PCA[25]、AC[10]、SR[8]、LMLC[16]、GS[13]、FT[26]、BFS[27]、SF[28]、MR[29]、GMR[29]、BSCA[30]、BL[31]在公开数据集MSRA1000、ECSSD 上进行比较，并从如下两个方面进行算法性能评估。

3.1 客观评价

将准确率-召回率（Precision-Recall，PR）曲线和算法综合指标F-measure作为评价指标，对本文算法和其余12 种算法进行分析比较。在实验中，逐步调整显著图Sfinal的阈值(0 ≤T ≤255)进行二值化，得到二值图S(x,y)，并通过公式（15）、公式（16）得到准确率precision和召回率recall，其中Gt(x,y)表示Ground Truth。F-measure 值由公式（17）得到。

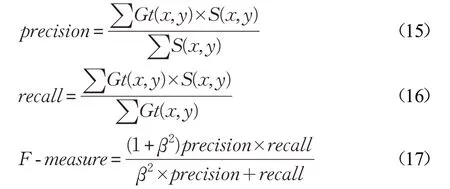
参考文献[28]，取β2的值为0.3。图7、图8 是本文算法和其他12种算法的实验对比效果图。

图7（a）是算法在MSRA1000 数据集上的PR 曲线图，通过分析比较发现本文算法与GS、BSCA、GMR 算法在准确率-召回率上较为接近，且高于传统的贝叶斯模型算法LMLC。通过图7（b）可以看出本文算法的Precion值和综合评价指标F-measure值明显高于其他算法，而Recall值明显高于MR、BFS、GMR等算法，与GS、BSCA相当。与GMR算法相比，本文算法的准确率、召回率以及综合指标F-measure指标均更优。综合这三项指标可以看出，本文算法在MSRA1000数据集上非常稳定，具有较好的鲁棒性。

图8（a）是算法在ECSSD 数据集上的对比结果，通过PR曲线发现在复杂背景下本文算法的准确率接近或优于其他算法，而召回率明显优于其他12 种算法。与BFS、PCA、BL、GS算法相比，本文的准确率和召回率略胜一筹。通过图8（b）可以看出本文算法的准确率优于GMR、BSCA等算法，而召回率与GMR、BSCA的相比要略微低一点，但准确率和综合指标F-measure 均高于其他算法。本文的准确率高于其他算法的原因在于由背景先验和凸包先验融合得到的先验图，能够更好地抑制背景噪声。从视觉效果上可以发现本文算法能够更加准确地突出显著目标，且有效减少了背景噪声，这方面要优于GMR、BSCA 算法。由于ECSSD 数据集中包含较多的复杂背景图像和多目标图像，导致检测效果要低于MSRA1000数据集的效果。

图7 MSRA1000数据集上的比较

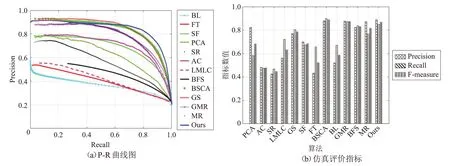
图8 ECSSD数据集上的比较

图9 各种算法的显著对比

3.2 主观评价

从视觉效果方面比较本文算法和其他12 种算法，如图9 所示，可以看出本文算法具有很好的视觉效果，且能够较好地抑制背景区域，突出显著区域，与真值图非常接近。通过对比发现，在平滑性方面，本文算法与MR、BSCA、GMR算法对应的显著图较为接近，与MR、BFS相比，显著图更加平滑，能够很好地抑制背景区域；在背景噪声消除方面，BSCA算法在处理复杂背景图像时会包含更多的背景噪声，而本文算法检测效果更加准确，背景噪声更少；在显著区域的完整性方面，与BSCA、LMLC 算法相比，本文算法检测到的显著区域更加完整。从图9中可以看出，本文算法得到的显著图轮廓更加清晰，背景噪声更少，显著目标更为突出。

4 结束语

本文提出的基于多尺度的贝叶斯模型显著性检测算法，在计算背景先验时利用多尺度超像素得到背景先验，同时利用凸包和多尺度超像素以及k-means聚类得到凸包先验，融合背景先验和凸包先验得到最终先验图。通过图像颜色直方图和凸包计算出似然概率，融合贝叶斯框架得到显著图，并对其进行优化得到最终显著图。在公开数据集MSRA1000 和ECSSD 上进行实验，得到的客观评价指标准确率、召回率以及综合性能指标F-measure都有很好的提升。但当图像中包含多个目标时，本文算法不能准确地对其进行区分。下一阶段的研究目标是如何更好地提高多目标图像的显著性检测效果。