高斯投影下的人机交互式物体仿真算法研究

杜丽美，连 玮

长治学院 计算机系，山西 长治046000

1 引言

物体重建技术是当今研究的热点问题之一，主要手段可以借助激光扫描技术、红外线测距技术或相关软件获取真实物体表面三维点云数据，由于测量误差的存在，通过各种途径获取的点云数据会掺杂噪声点，所以从物体表面获取较高质量的点云数据直接影响后期的物体重建效果。一般从物体表面获取的三维点云数据量非常庞大，针对不同的物体可能需要提取成千甚至上万的数据点，如果直接将这些数据点显示在屏幕上，虽然也可以展现出物体的全貌，但是却得不到一个完整的物体，因为物体由点描述其结构较松散，导致无法使用在一些专业领域中，所以要做的是将这些点云数据重构出相应的面片，使其成为一个结构完整的整体。物体的重构技术可以应用到许多领域、比如医学重建、古建筑物修复、3D打印等。

文献[1]提出一种点云融合技术，在重建过程中采用类似投影的方式重建网格模型，最终将重建的模型用于3D 打印过程中。文献[2]采用物体重建的方法对建筑物损伤部位进行修复，重建过程借助最小二乘法原理进行曲面拟合达到了很好的效果。文献[3]对苹果树叶片进行三维重建，用到了包围盒法对点云数据进行去噪，又用到了精简算法对点云数据进行精简，最后使用Delaunay 三角网格划分算法进行了重建。以上文献中介绍了不同的网格重建算法，这些算法只是针对解决特定的问题提出，因而本身具有很大的局限性。本文将提出一种通用的网格划分算法用来对给定的物体进行仿真重建。

2 点云数据处理

利用三维激光扫描技术，通过三维激光扫描仪发射出来的光束，照射到物体表面，从而获取到物体表面的三维点云数据坐标，并将数据保存在后缀名为.obj的文档中，保存格式如图1所示，图1所示文件中第一行为该物体的纹理信息，存储在.mtl 的文件中（若物体没有纹理特征，则删除本行），以“v”开头的信息即为扫描到的三维数据点坐标。采用相应的数据结构存储图1 中的数据点（注意：这里定义的数据结构应至少包括点的三个坐标值，点的索引值，以及指向前一个点和后一个点的指针），由于数据点中必定掺杂噪声，所以第一步要做的就是进行去噪处理，由于采集了大量的数据点，这里可以采用概率统计中的方法来去噪[4-5]，去噪思想是通过球内大量点的数据信息估算出点的大致规律，如果目标点满足这一规律则留下，否则去掉。

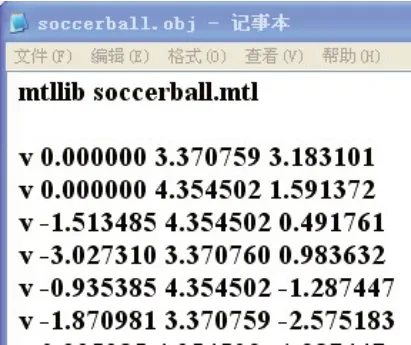
图1 点云数据的存储

具体的去噪方法如图2所示：要判断点P 是否为噪声点，先以P(X0,Y0,Z0)为球心，以r 为半径作球（r 的值根据实际情况自行设定），利用公式（1）判断所有数据点哪些落在球内部，设集合A 中的点{p1,p2,…,pk}均为落在球内部的点，然后分别计算集合A 外的所有点到集合A 中p1 的平均距离、p2 的平均距离、…、pk 的平均距离，利用公式（2）和（3）求出这些平均距离的平均值μ 以及方差σ2：

图2 去噪过程

3 初始网格模型的构造

由于物体表面的点云数据都是三维点的坐标，直接对这些点进行三角网格的划分会导致难度过大，而且效率低下。目前为止人们对于二维数据点的三角网格划分算法研究得比较成熟，而且算法相对简单，为此本文的主要思想是先将三维数据点投影到二维平面上，如果直接进行投影，必定会改变点与点之间的位置信息，导致重建出的三维模型不准确或者是失真等现象，本章将提出一种新的投影方法来解决此问题。

3.1 分区域生成三角网格

为了保证将三维数据点投影到二维平面上后，点与点之间的角度等信息不变，这里将使用高斯投影的方法，高斯投影是一种等角投影方法，借助地理坐标系统中经度和纬度的概念，主要思想是将椭球面按一定的经度间隔划分成若干区域块，然后分别将每个区域块的点投影到二维平面上，这种投影方法可以保证椭球面上的点在投影前后的相对位置保持不变。

利用高斯投影[6-7]的思想，这里将椭球面看成圆球，首先求出点云数据在X 方向上的最大长度length Y 方向上的最大宽度width以及Z 方向上的最大高度height，设定圆球的半径为R=max(length,width,height)/2，球心为O(length/2,width/2,height/2) ，也就是所作圆球内要包含所有点云数据如图3所示，然后从球心分别指向每一个数据点的射线必定与球面交于一点如图4 所示，例如球心与数据点P 的连线交球面于点P′，那么点P 与P′就建立了一对一的关系，P′的坐标可以由相应的经度和纬度表示，如图5 所示，作P′在XOY 平面上的垂线并交于P″，则∠P″OX 所对度数为点P′的经度用α 表示，∠P′OP″所对度数为点P′的纬度用β 表示，设P′坐标为(x,y,z)，由于此时的球心坐标并不是（0，0，0），故先使用公式（4）计算OP' 的坐标，然后经度α 和纬度β 可由公式（5）和（6）求出。

图3 作圆球包含所有数据点

图4 球心与数据点连线

图5 计算P′的经度α 和纬度β

由于点云数据点较多，直接投影难免会遇到一些未知错误，所以这里借助大地经度和纬度的知识，将球面按经差n 度进行分带（n 可以选择6的整数倍，如6，12，18，24 等），这样球面会被划分成360/n 个区域，将每一区域中的点云数据采用简化后的高斯投影公式（7）和（8）分别投影到二维平面中，得到对应的二维数据点坐标(x,y)，公式中的R 为球面半径，β 为点的纬度，l 为点的经度与中央子午线经度的差值（此处的中央子午线经度值指的是每一带的中间位置所对的经度值）。公式（7）和（8）中的A、A′、t、ρ 分别由公式（9）、（10）、（11）和（12）给出。

对每一区域内投影到平面上的二维数据点进行三角网格的划分如图6所示，重点得到二维平面上点与点的连接关系，将这种连接关系反映射[8-10]回原三维数据点上，即完成了每一区域内三维数据点的网格划分。

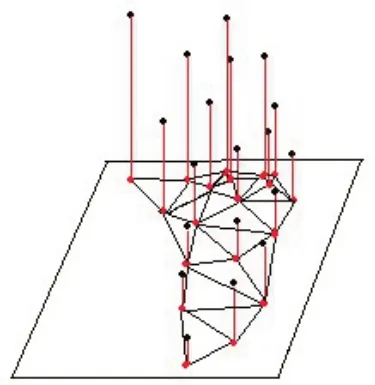
图6 高斯投影演示

3.2 区域间拼接

由3.1节中的算法可将每个区域内的三维数据点进行三角网格的划分如图7所示，本节主要完成区域间的拼接。要想进行区域间的无缝拼接，第一步就是提取图7 中每个区域的边界信息如图8 所示，假设这些区域为S1,S2,…，对于区域S1的边界提取具体做法为：

（1）首先找到S1中第一个边界三角形D0，在区域S1中随机取出一个三角形D，判断该三角形的三条边是否有向外延伸的其他三角形，如果D 的三条边均有向外延伸的其他三角形，则表明D 不是边界三角形，继续判断D 周围的三角形；如果D 中某些边没有向外延伸的三角形，则表明该三角形是边界三角形，记为D0，并将边界边的信息（包括边和两个顶点）存储在指定数据结构Edge和Vetex中。

（2）找到第一个边界三角形D0后，就可以逐步判断与D0有公共边的那些三角形是否为边界三角形，如果是则将相应的边界边的信息存储在Edge和Vetex中。

（3）按照上面步骤的方法，将区域S1中找到的边界边的信息都存储在Edge 和Vetex 中。为了保证能够寻找到所有的边界边，可以将Edge中的边首尾顺次存储，如果所有边构成了一个环，说明找到了所有的边界边，其中Edge对应的数据结构如图9所示。

图7 区域内网格划分

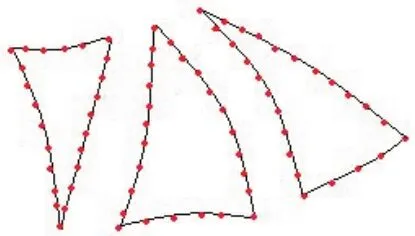
图8 每个区域边界提取

图9 边界边的存储

根据上面的步骤最终找到了每个区域S1S2…的边界边和边界点，接下来要做的就是实现区域间的无缝拼接，根据3.1节的方法将整个点云数据划分成了360/n个区域，即有360/n 个Edge和Vetex数据结构。在这些区域间进行无缝拼接，其实就是将所有Edge 中的边和相邻区域Vetex 中的点进行三角网格划分的过程，但是要保证如下两个条件成立：

（1）一个区域中的边只能和其他区域的点形成边。

（2）新形成的边不能和所有Edge中的边相交，也不能和新边相交。

区域与区域之间进行拼接的具体做法为：

（1）先从第一个区域S1中的第一条边界边为出发点，向外寻找相邻区域Vetex中的边界点，然后边和点构成三角形，但要满足如上两个条件。比如以边界边AB为例，其中点A 坐标为(x1,y1,z1)，点B 坐标为(x2,y2,z2)，然后在其相邻区域的Vetex 中寻找边界点，可以采用如图10 的方法，寻找距离边AB 的中点O 最近的点P ，为了保证点P 的选取确实在边AB 的相邻位置，可以先判断线段OP 的长度是否小于给定的阈值T0（阈值T0为点O 到相邻区域中的最高点与最低点所在的直线的距离），然后判断PA 与PB 会不会与其他边相交，若PA 与PB 不与其他边相交，则可构成△PAB，继续寻找下一条边界边对应的边界点，直到区域S1中的边都遍历到为止。

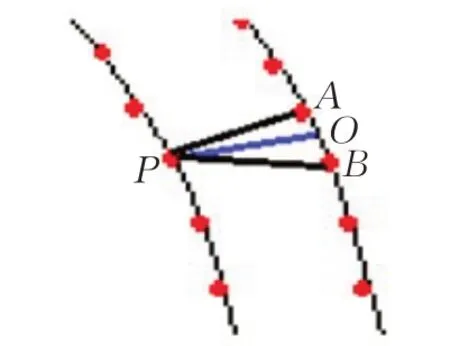
图10 边界间拼接

（2）再从区域S2中的边界边出发，首先检查每条边是否已经与相邻区域的边界点构成三角形，如果没有，那么采用步骤（1）的方法寻找相邻区域的边界点构成三角形。

（3）参照步骤（2）的方法，对其余区域的边界边向外寻找边界点，直到360/n 个区域中的边界边都与其他区域的边界点构成三角形，停止。

这里要补充说明，三维空间中的边与边之间的关系有三种：平行、异面和相交。设有两点A(x1,y1,z1)和B(x2,y2,z2) 组成的边AB ，以及两点C(x3,y3,z3) 和D(x4,y4,z4)组成的边CD，则AB 和CD 所在直线可用两点式表示，若AB 与CD所在向量对应成比例，则表示AB 与CD 平行；若公式（13）成立，则表示AB 与CD 共面；若公式（13）不成立，则表示AB 与CD 异面。若AB与CD 共面且不平行，则还要继续判断线段AB 与线段CD 是否相交。

判断线段AB 与线段CD 是否相交，首先可以使用x 坐标或y 坐标或z 坐标的位置来判断，具体为判断一条线段较大的x 值是否小于另一条线段的较小的x值，如果是，则表明两线段没有交点；或者判断一条线段的较大的y 值是否小于另一条线段的较小的y 值，如果是，则表明两线段没有交点；或者判断一条线段的较大的z 值是否小于另一条线段的较小的z 值，如果是，则表明两线段没有交点。相应的算法可由公式（14）实现，若公式（14）的值为1 则表明两线段不可能有交点。若公式（14）的值为0，则需采用向量叉乘法继续判断是否相交，判断方法为：如果公式（15）成立，则表明A 点和B 点在线段CD 的两侧；如果公式（16）成立，则表明C点和D 点在线段AB 的两侧；公式（15）（16）同时成立，则说明线段AB 与线段CD 相交（注：“×”为差乘，“·”为点乘）

3.3 优化模型

通过以上步骤已经建立了最初的三角网格模型，但是考虑到从物体表面提取的数据点有些是处在一个平面上的，而在同一平面上生成的三角网格是没有任何意义的，为了精简模型中三角形的数目，需要对模型进行优化处理[11]。

计算所有三角形面片所在的法向量，针对每个三角形面片判断是否与其相邻的三角形面片共面，若共面则将这些共面三角形的公共边去掉融为一个多边形，从而达到优化模型缩减网格数量的目的。

4 人机交互细分网格模型

以上建立的初始网格模型只是还原了物体概貌，模型表面还不是很光滑，重建出来的模型棱角较多失真现象严重。本章将通过人机交互的方式，对初始网格进行插值细分，以期达到物体表面光滑的效果[12-13]。由于物体表面可能存在三角形面片和多边形面片两种，对于这两种不同形态的面片，分别使用不同的细分方法。

如果要细分的是三角形面片，这里采用Bezier曲面来寻找新的控制点，三次Bezier曲面可由10个控制点来确定，这10个控制点对应在△ABC 上的大致位置如图11 所示，分别为P003、P300、P030、P102、P201、P012、P021、P210、P120和P111。其中P003、P300和P030为△ABC 三个顶点的坐标，只需要根据公式求出其余7个控制点的坐标。这7个控制点的坐标可由文献[13-14]中的方法求出，重点得到控制点P111的坐标，然后P111与△ABC 的三个顶点相连，这样就实现了三角形的细分。

如果要细分的是多边形面片如图12 所示，可以借助此多边形面片周围的三角形面片来实现细分过程。首先找到与其存在公共边的邻域三角形，如图13 所示的邻域三角形有△1、△2、△3、△4 和△5。以△1 为例，△1 与多边形存在公共边，在△1 上进行Bezier 曲面插值的时候，此公共边上会生成两个新的控制点，如图11 所示这两个新的控制点可能是P012、P021，同理可以求出其他三角形△2、△3、△4 和△5 与多边形的公共边所对应的新的控制点，将这些控制点取平均值，即为多边形面片新的控制点P11，最后如图13 所示将P11与多边形的各个顶点连接，这样就实现了多边形面片的细分。

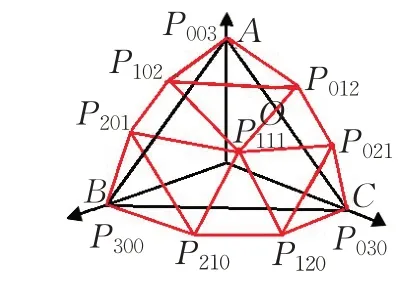
图11 寻找新的控制点

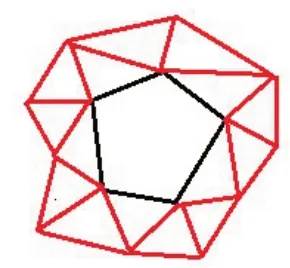
图12 不规则多边形的细分

图13 寻找新的控制点

对于本章的细分过程，可借助OpenGL中的函数来实现人机交互的效果[15-16]，具体可由键盘上的按键来控制细分的次数以及控制物体的旋转、缩放和平移。本文实现了由键盘上的A 键控制细分的次数，F1、F2、F3 和F4 键控制物体的上、下、左、右旋转，F5 和F6 键控制物体的缩放，↑、↓、←、→箭头控制物体的上下左右平移。式（17）为OpenGL中处理普通按键比如字母、数字等消息的函数，式（18）为OpenGL中处理特殊按键比如箭头、F1等消息的函数。

式（17）和（18）中的func 函数为当按下相应按键后，需要调用的函数，x 和y 为当按下按键时鼠标相对于窗口左上角的位置。

此外还可以对仿真出的模型进行光照和材质等的设置，使模型更加逼近真实物体，具体的光照函数为式（19）所示，其中参数1表示要创建的光源号，参数2表示光源特性，参数3表示光源特性值。材质设置函数为式（20）所示，其中参数1 表示将当前材质作用在哪个面上，参数2表示材质特性，参数3表示材质特性值。

5 实验结果

为了验证本文提出算法的正确性，这里采集了各种物体表面的离散数据点，图14 的物体是每个面都为五边形的球面（正十二面体），图15的物体是一只兔子，图16的物体是一只球鞋。

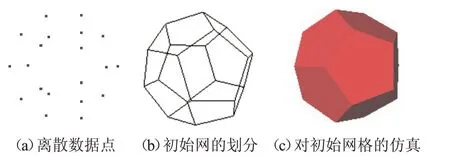
图14 正十二面体仿真过程

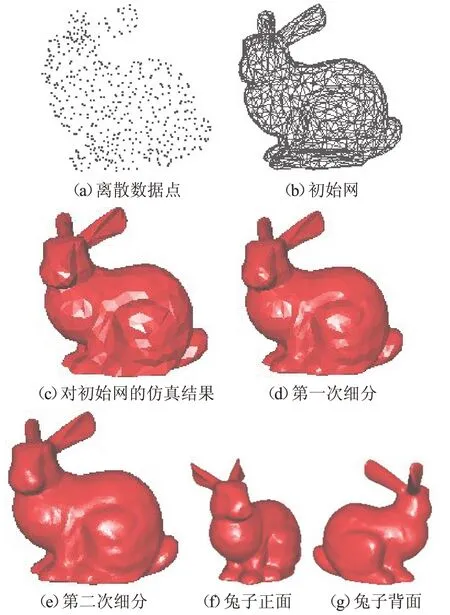
图15 兔子仿真过程

图14 中的正十二面体，共采集了20 个数据点如图14（a）所示，通过初始网格划分以及优化模型，共形成了12个正5边形面片如图14（b）所示，对图14（b）进行光照和材质等的设置如图14（c）所示，要注意的是对于这里仿真的正十二面体，不需要进行网格的细分过程，否则会破坏正十二面体的表面结构特征。

图15 中的兔子，共采集了502 个数据点如图15（a）所示，图15（e）为对初始网格进行两次细分后的结果（这里的细分采用键盘上的A键来进行，细分一次按一次A键，细分两次按两次A键），通过两次细分物体表面近似光滑。图15（f）和图15（g）为使用键盘上的按键来控制兔子的方向，从而实现人机交互展现出兔子的正面结构和背面结构。

图16 中的球鞋，共采集了1 841 个数据点如图16（a）所示，图16（b）为优化后的初始网格模型，最终形成的初始网格中包括三角形面片和四边形面片两种，图16（d）为图16（c）的放大效果。图16（e）为经过一次细分后球鞋表面的光滑效果，图16（f）为经过第二次细分后球鞋表面的光滑效果。图16（g）和图16（h）为在键盘控制下球鞋的各个角度展示。

图16 球鞋仿真过程

图15 与图16分别对兔子与球鞋模型进行了两次细分，第一次细分后的仿真效果要比直接对初始网格的仿真效果较光滑，但是还存在一些不光滑的棱角区域，为此又进行了第二次细分，通过第二次细分后几乎看不到之前的棱角部分，模型表面已经很光滑几乎接近真实物体表面。

以上三个物体在重建过程中每个阶段的数据统计见表1所示，表中第三列区域个数(QY)指的是第3.1节中所述的划分区域的问题，其中要注意的是对于兔子模型的重建，需要将兔子耳朵单独分割出来进行。表2为对于球鞋模型使用本文所提算法和使用传统的区域生长算法进行重建的相关参数比较，从表中可以看到对于同一批球鞋数据点，使用本文算法形成的初始网格个数要少于区域生长算法，原因在于本文算法在生成初始网格的过程中进行了模型的优化处理。从时间上来看，本文算法比较占优势。表1 和表2 中num 表示从物体表面采集的数据点个数，QY 表示划分的区域个数，m0表示初始网格个数，m1 表示第一次细分后网格个数，m2 表示第二次细分后网格个数，t 表示运行时间，d 表示细分次数。

表3 是判断兔子表面某一点P 是否为噪声点的部分数据展示，若P=（-0.170 739，0.219 018，0.013 140），以P 点为球心，r=0.06 为半径做球，落在球内部的点有27个，点P 到这27个点的距离见表3所示，由此可算出点P 到这27 个点的平均距离为0.041 6，再通过这27 个点利用公式（2）和（3）计算出相应的取值区间为（0.038 9，0.123 0），因为0.041 6 ∈（0.038 9，0.123 0），所以点P 是正常点。

表1 物体仿真数据

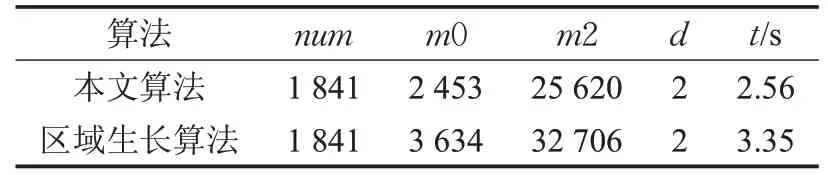
表2 本文算法与区域生长算法比较（球鞋）

表3 r=0.06 时球内部的27个点到点P 的距离

6 结语

本文实现了人机交互式的物体仿真建模过程，建模过程中使用了地理坐标下的高斯投影算法，在细分时使用了Bezier 曲面的插入控制点的方法，最后使用OpenGL中的键盘控制函数、光照函数、材质函数等完成了重建过程。本文所提算法可以很好地应用于古建筑物的修复或者3D打印等领域中。

相比其他算法，本文算法可以对大部分表面较为光滑的物体进行重建，但是本文算法也有很多不足之处，比如在进行初始三角网的构建时，使用高斯投影的思想是将三维数据点投影到二维平面上再进行三角网的划分，这种方法对于原始物体表面存在孔洞或是多处存在大幅度的凹陷的情况不是很适用，为此物体重建算法还是今后研究的重点方向之一。