考虑客户吸引力的轴辐式海运网络优化
2020-06-09陈访剑韩晓龙
陈访剑,韩晓龙
上海海事大学 物流科学与工程研究院,上海201306
1 引言
海上运输作为国际运输方式之一,承担了全球贸易货量近90%的运输任务。与传统的全连通海运网络相比,轴辐式集装箱海运网络更符合世界贸易格局的网络结构特性,也能产生更明显的规模经济效益,引起了学术界及航运界的广泛关注[1]。航运企业在航线的运营过程中所获得的利润,受多种因素的影响。如何规划轴辐式集装箱海运网络,选定枢纽港口,确定非枢纽港口和枢纽港口的连接关系是轴辐式海运网络设计研究的重心[2]。
已有的文献在进行海运网络设计时考虑的因素分别有航速[3]、网络脆弱性[4]、碳排放成本[5]、节点容量限制[6-7]等,尽管研究特定某个因素对网络设计的影响方面有一定的意义,但是所研究的内容较为片面,而现实中航线网络设计会受到多种因素影响。考虑客户吸引力因素对航线网络设计的作用的文献并不多,吸引力模型最初起源于万有引力定律,而在此基础上改进的公式已经在地理、经济、贸易等领域得到了广泛的应用。在经济贸易领域里,它常被用来计算各种贸易流[8],在交通运输领域,常被用来预测预期货流量或航空客流量[9-10],在对客户进行行为选择分析时也有重要作用。
尽管海运市场是一个具有寡头垄断特点的市场,但也遵循着一般的市场经济规律,即承运企业提供的海运服务对托运人存在吸引力,会影响托运人的选择。
Reilly最早提出了确定性的吸引力模型,在这之后,Huff[11]将Reilly的吸引力模型做了延伸并将其应用在零售贸易领域,提出潜在客户的选择行为会受到服务的便利性的影响,构建了客户的吸引力模型,但是没有考虑产品或服务的价格影响因素。Eiselt等[12]在竞争性的航空市场环境下,使用引力模型作为效用函数,以航空公司抢占客户流量最大为目标建立模型,为后进入市场的航空公司(跟随者)在选定枢纽、规划航线等方面给出了决策建议,对集装箱海运网络的规划也具有启发意义。王杰等[13]对经典引力公式进行了改进,通过考虑节点适应度、节点之间的距离、节点货运量规模等因素来对班轮航线上节点对的货流量进行预测,从而构建集装箱班轮网络,以东亚区域主要港口构成的海运网络进行实例分析,验证了模型的有效性。Gelareh等[14]基于服务时间和服务成本等因素,研究了竞争的航运市场环境中跟随者的竞争策略,存在着一定的不足:一是没有考虑所设计的网络结构对航线运营的影响,如航线的安全性、稳定性等;二是采用了基于弧的变量来构建模型,在求解运算时,基于路径的变量在效率上更有优势。同样是竞争环境下的海运网络设计研究,赵宇哲等[15]突破了枢纽港口集合是给定的假设,引入基于服务约束的吸引力模型来定量表示客户的选择行为,以利润最大为目标建立模型,并使用基于增广Lagrange 函数的算法进行求解,但没有考虑航运企业所获利润受客户对服务的不同偏好的影响。
另一方面,近年来温室气体的过量排放既危害自然生态系统的平衡,也严重威胁着人类的生存环境,研究碳排放对航运业的影响成为了国内外学者研究的一个热点方向[16-17]。鉴于此,本文所建的轴辐式海运网络模型也考虑了环境成本(主要是碳排放成本)对航运企业经营利润的影响。
综上,相关文献普遍存在的问题是模型中研究的影响因素较为单一,对客户吸引力相关因素考虑得不够全面,特别是客户对服务的偏好所产生的影响研究较少。本文在借鉴已有研究的基础上,综合考虑了影响航运利润的环境成本、运输成本等因素,引入客户吸引力模型,研究客户吸引力与集装箱货运量之间的关系,以海运网络利润最大化为目标建立模型,为航运企业进行航线优化提供参考。
2 问题描述与建模
2.1 问题描述
轴辐式集装箱海运网络一般采用单分配形式,即非枢纽港口只能连接一个枢纽港口。枢纽港口之间由干线相互连接,非枢纽港口与枢纽港口之间由支线连接,非枢纽港口之间不能直接连接,集装箱中转只能在枢纽港口进行。
定义轴辐式集装箱海运网络(如图1所示)为G(N,A),其中N 为港口节点的集合,A 为网络中节点之间的弧的集合,也就是港口节点之间的所有可行的航线连接的结合。对于任意的港口i j ∈N ,定义ij ∈A 为由港口节点i 到港口节点j 之间直接连接的航线。实际中集装箱中转的港口数量一般不超过两个[6],又考虑到本问题中非枢纽港之间不能直接连接的假设,因此,港口i j 之间的连接情况有以下三种情况:(1)港口i j直接相连,即港口i j 都是枢纽港;(2)港口i j 间的集装箱运量通过一个枢纽港中转,则港口i j 是分配给同一个枢纽港的两个非枢枢纽港口,或者i j 中一个是枢纽港一个是非枢纽港;(3)港口i j 间的集装箱运量通过两个枢纽港口中转,这种情况下可能的一条集装箱流向为i →k →l →j(k 为港口i 所连的枢纽港,l 为港口j 所连的枢纽港)。
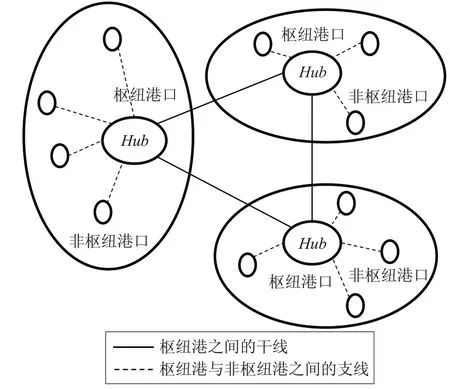
图1 轴辐式海运网络结构
轴辐式集装箱海运网络设计问题的关键是:确定轴辐式集装箱海运网络G 中的枢纽港口[18]及其所辐射的非枢纽港,并根据集装箱OD需求情况制定合理的航线优化策略。对一个航运企业而言,枢纽港口节点与航线规划的最优方案应该使海运网络所承担的运输任务的总利润最大。模型的目标函数设计中所考虑的成本结构有:集装箱运输收入、集装箱运输成本、枢纽港口中转成本以及集装箱运输的环境成本。
值得注意的是,航线上集装箱运输的收入与该航线上的货运需求量成正相关,本文假设该航运企业所经营航线上的货运需求量会受到基于服务水平的客户吸引力的影响[15],这部分会在下一节作详细说明。
2.2 客户吸引力概述
航运市场上有多个航运企业,它们所提供的港口i →j 间的海运服务具有较强的同质性。托运人一般会选择综合效用最大的方案提供者提供服务,在选择时主要考虑三个因素:一是基于运输航线的服务质量Sklij;二是集装箱运输服务的单位运输价格Pij;三是基于航线连接的运输时间。详细说明如下:
(1)服务质量
港口的服务质量与港口的地理位置、经济、政策、安全性、自动化程度等因素有关,是个综合评价指标。由于集装箱海运操作层面的作业任务主要是在港口进行,因此,航线的服务质量就由该航线所经过的所有港口的平均服务质量来表示。在本文所研究的轴辐式海运网络的情况下,假设运输经过枢纽港k l 中转,运输路径为i →k →l →j,则该航线的服务质量的表达式为:

其中,SiSkSlSj分别表示港口i k l j 的服务质量。
(2)单位运输价格
从港口i 运到港口j 的单位集装箱的市场价格为Pij,设价格稳定并在较长时间内不变。
(3)运输时间
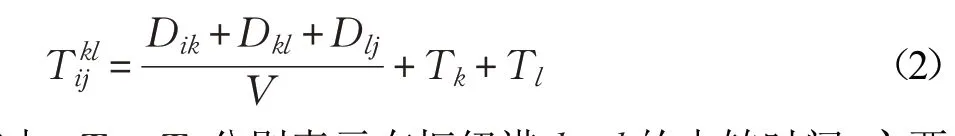
运输时间主要包括运输船舶的在途时间和挂靠港口时的中转时间。在本文所研究的轴辐式海运网络中,若船舶经枢纽港k l 中转,则运输时间表达式为:其中,TkTl分别表示在枢纽港k l 的中转时间,主要由港口自动化水平及管理状况决定。由此可见,航线的服务质量与运输时间主要取决于起讫港口i j 之间的航线连接设计。
鉴于一些运输领域的研究中已经使用过吸引力模型,并且验证了其在行为选择分析方面起到的作用,因此得到航运企业所提供的航线吸引力的表达式:

其中,ω 和λ 为一组关于单位服务价格Pij和运输时间的灵敏系数,表示吸引力的减少速度与单位服务价格Pij和单位服务时间的增加速度是一致的[15],θ 和(1-θ)为一组关于单位服务价格Pij和服务时间的权重系数,能体现出客户吸引力受服务价格与服务时间影响的偏重程度。
本文站在某一航运企业的角度,为其提供航线设计优化决策。若优化后的海运网络的某条航线具有更强的客户吸引力,该航运企业就能夺取该航线上其他航运企业的货源;若航线的吸引力减弱,则会失去部分货源。也就是说,航运网络经过优化后,从港口i 到港口j 的运输路径可能会发生改变,由此带来的航线客户吸引力的变化会导致i →j 的集装箱货运量改变。设优化后i →j 航线的货运量为Qij1,旧航运网络上i →j 航线的货运量需求量为Qij0,新旧网络中i →k →l →j 航线上的客户吸引力分别为,则它们之间存在以下关系:

2.3 模型假设与参数定义
问题的基本假设如下:
假设1 模型中所有港口节点之间的相对地理位置已知且固定,不考虑自然灾害、局部战争等突发情况的影响。
假设2 枢纽港口的容量及船舶载运能力足够满足运输需求,船舶的航速已知且不考虑枢纽港口容量限制约束。
假设3 轴辐式集装箱海运网络存在规模经济效应并且枢纽港口之间的单位运输成本折扣率为已知。
假设4 任意两个港口之间的单位运输价格及成本为已知,任意港口的中转固定费用与中转时间均为已知,装卸费用与集装箱运输量成线性正比关系。
假设5 集装箱OD 的环境成本仅考虑运输过程中产生的碳排放成本,不考虑船舶在港口作业时产生的环境成本。
假设6 枢纽港之间两两相连,非枢纽港之间不直接连接。
相关参数:
N 为网络中所有港口节点集合;
h 表示需选定的枢纽港口的数量;
Qij表示港口i j 之间的集装箱货运量(TEU);
Pij表示港口i j 之间单位集装箱运输服务的价格(USD/TEU);
α 表示枢纽港间的规模经济折扣率(0<α<1);
Cij为直接连接的两港口间的单位集装箱运输成本(USD/TEU);
Dij为港口i j 间的距离(NM);
hk为枢纽港口k 的中转固定费用(USD);
Tk为船舶在枢纽港口k 的中转所需时间(h);
ρk为船舶在枢纽港口k 的单位集装箱装卸费用(USD/TEU);
V 表示集装箱船的速度(knot);
FV表示集装箱船以速度V 航行时的平均单位集装箱重油(燃料油)的消耗量(t/TEU·h);
β 表示重油的碳排放因子(二氧化碳吨/燃油吨);
C 表示碳排放税率(USD/二氧化碳吨)。
决策变量:
Yi为枢纽港口节点选择变量。若港口i 被选为枢纽港,则Yi=1,否则Yi=0。
Zik为非枢纽港i 与枢纽港口k 的连接选择变量。若港口i 与枢纽港口k 连接,则Zik=1,否则Zik=0。
2.4 模型构建
基于以上问题假设和参数定义,分别建立一般情况下的轴辐式海运网络设计模型M1、考虑客户吸引力的因素建立轴辐式海运网络优化模型M2,并将两者作对比以证明优化模型的优越性。
2.4.1 轴辐式海运网络设计模型
在不考虑客户吸引力因素情况下,构建航运企业进行轴辐海运网络设计的模型M1,如式(5)~(18):

式(5)表示模型的目标函数为海运网络的总运营利润最大;式(6)表示该集装箱航线运输的总收入为C0;式(7)表示该集装箱航线运输的总运输成本为C1;式(8)表示该集装箱航线运输的总挂靠成本为C2;式(9)表示该集装箱航线运输的总环境成本为C3;式(10)保证网络中枢纽港口总数等于h;式(11)表示当且仅当港口h l 被选为枢纽港时,集装箱运输才能经过枢纽港口h l 进行中转;式(12)表示任意两港口之间的集装箱货物只能通过一条航线运输;式(13)表示非枢纽港口所连接的必须是枢纽港;式(14)表示任意非枢纽港口只能分配给一个枢纽港口;式(15)、(16)表示起讫港口i j 之间的集装箱运输所经过的港口必须是枢纽港口,不能通过非枢纽港口中转,且不允许超过2 个枢纽港口;式(17)表示若存在航线连接为i →k →l →j,则港口i 必定与枢纽港k 连接;式(18)表示决策变量都是0-1变量。
2.4.2 考虑客户吸引力的网络设计模型
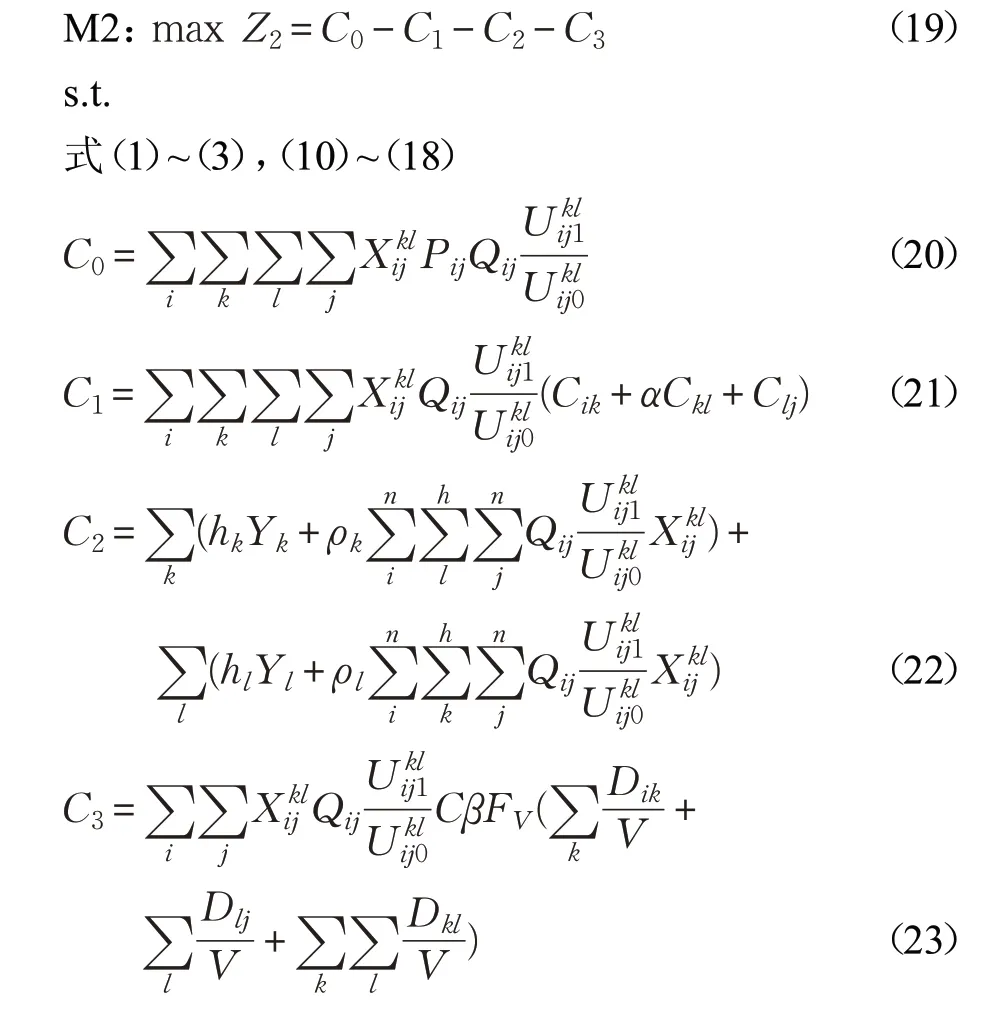
式(19)表示考虑客户吸引力的模型目标函数为海运网络的总运营利润最大;式(20)表示模型总收入为C0;式(21)表示模型总运输成本为C1;式(22)表示模型总挂靠成本为C2;式(23)表示模型总环境成本为C3。
3 基于遗传算法的模型求解
模型M1与模型M2均为非线性的0-1规划问题,难以在多项式时间内使用精确算法(如分支定界法、隐枚举法等)求解该NP-难问题。在实际应用中,通常使用启发式算法对该类问题进行求解,而模拟退火法、蚁群算法、免疫算法等由于受到所研究问题性质的局限,容易出现求解时间过长和容易陷入局部最优解等问题。与上述算法相比,遗传算法通过交叉、变异等操作能够比较有效地避免陷入局部最优,设置合适的参数能提高遗传算法全局搜索的广度和深度。而且遗传算法灵活性强,对于求解变量是离散的非线性0-1 规划问题具有一定优势。鉴于此,考虑到所建模型的特征,本文设计了双层编码的遗传算法来求解该问题。
3.1 编码方法及种群初始化
根据前文假设,港口节点数量为N ,枢纽港数量为h。
第一层编码为选择枢纽港的顺序编码,编码长度为N ,基因为从1到N 的自然数的一个不重复排序;第二层编码为分配各个非枢纽港口到其对应枢纽港的编码,为长度为N 的整数编码,基因位上的值取大于等于1且小于等于h 的整数。由于在解码时只选择前h 个编码作为枢纽港,确保了枢纽港总数能够满足式(10)的约束条件。
假设N=5,h=3,则一个合法的染色体可表示为[5,4,2,1,3,1,3,3,2,1]。第一层编码为[5,4,2,1,3],选择该编码的第1至h 位编码作为枢纽港,h=3 则港口5、4、2 为枢纽港;第二层编码为[1,3,3,2,1],则表示港口1 被分配到第1 个枢纽港,港口2 被分配到第3 个枢纽港,港口3 被分配到第3 个枢纽港,港口4 被分配到第2 个枢纽港……以此类推。该编码方式能保证任何一个港口只能被分给一个枢纽港,即能满足式(14)的约束限制。
其他的约束条件,在求解软件的程序语句以条件限制或惩罚函数的方式明确描述,从而使模型中的约束得以满足。
按照上述编码方式生成初始种群,并设置初始种群规模。
将模型的目标函数值的相反数作为适应度函数。这样,适应度值越小则表示所对应的个体越好。
3.2 变异运算
在第一层编码中,为避免单点随机变异产生不合法的染色体,采用两点互易的规则进行变异。首先产生两个随机自然数r1、r2,然后交换第r1 位和第r2 位的基因。如r1=2,r2=4,则染色体[1,3,2,5,4]变异为[1,5,2,3,4]。
第二层编码采用单点随机变异的方法。
3.3 交叉运算
按照交叉概率从不同的父代中选择两个染色体作为父本,并产生2个随机自然数r3、r4。将两个父本染色体r3 至r4 之间的基因片段进行交换,得到两个子代染色体。
第一层编码在进行交叉操作时,需要对交叉后的两个染色体进行修正处理,这是为了避免染色体内基因冲突。第二层的编码不需要进行修正操作。修正方法为:在交叉后,将交叉片段的补集重新排列到非交叉片段,使染色体内不发生冲突。假设第一层编码长度为5,r3=2,r4=4,交叉过程示例如图2所示。
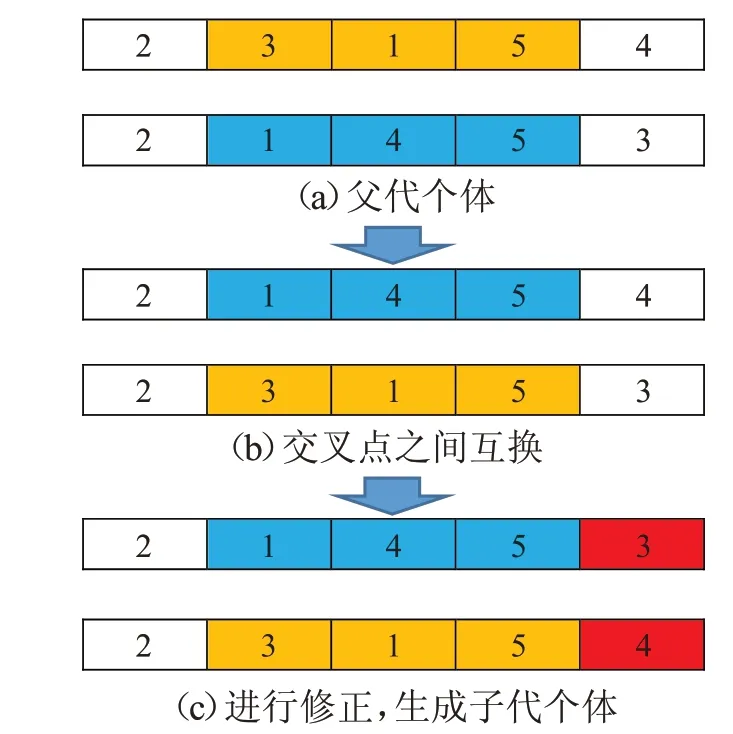
图2 交叉过程示意图
第二层编码的交叉运算过程与第一层编码相似,但是不需要进行修正操作。
3.4 选择运算
本文使用轮盘赌选择法,各个体被选中的概率Pri与适应度值Fi成正比。适应度越高的个体更容易遗传到下一代的种群中去。设种群规模为R,则:

3.5 遗传算法求解模型流程图
本文使用遗传算法求解模型的基本流程如图3所示。
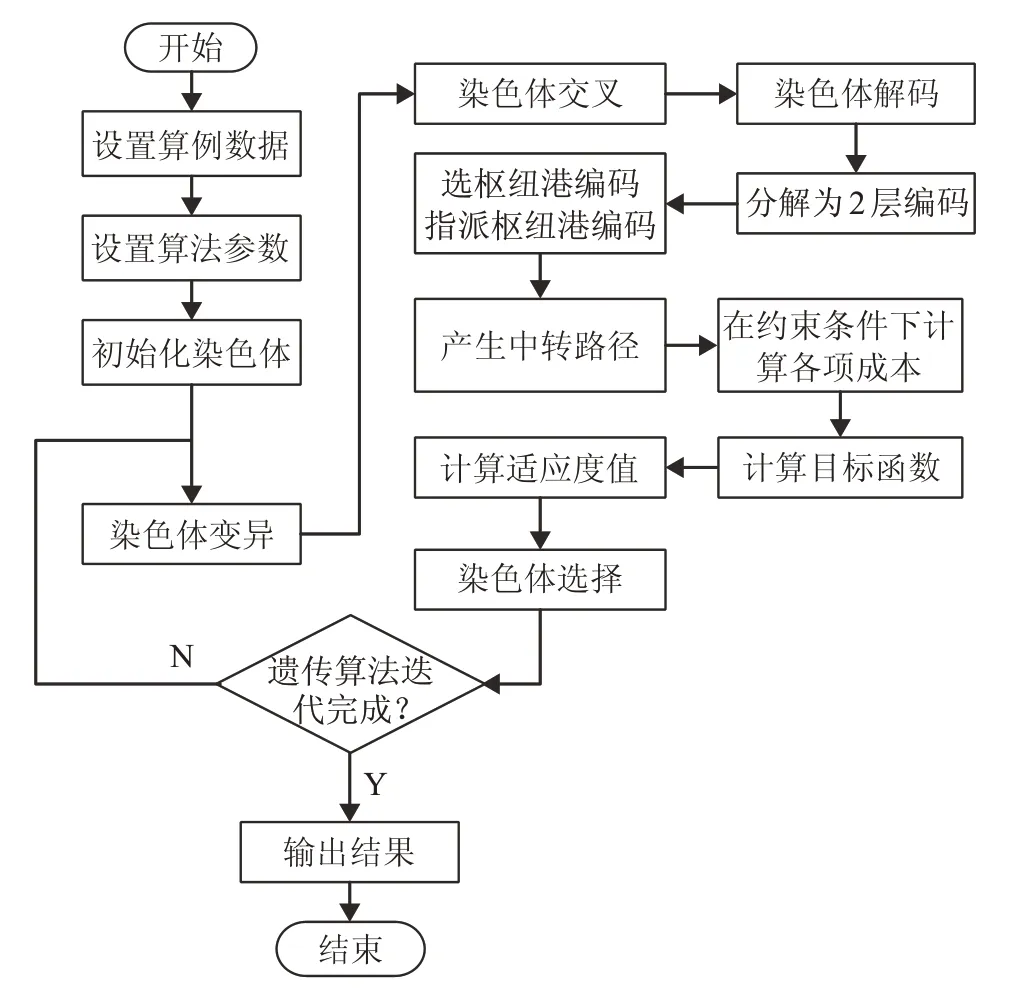
图3 遗传算法求解模型流程图
4 算例分析
4.1 数据选取
假设港口节点数量N =20,任意一个港口k 作为枢纽港口时的中转固定成本hk服从正态分布N(500,100);单位装卸费用ρk服从正态分布N(7,1);中转服务时间Tk服从正态分布N(20,3);服务质量Sk服从正态分布N(100,30);港口位置的横、纵坐标随机产生,服从均匀分布U(0,10 000)。生成的港口相关数据如表1所示。
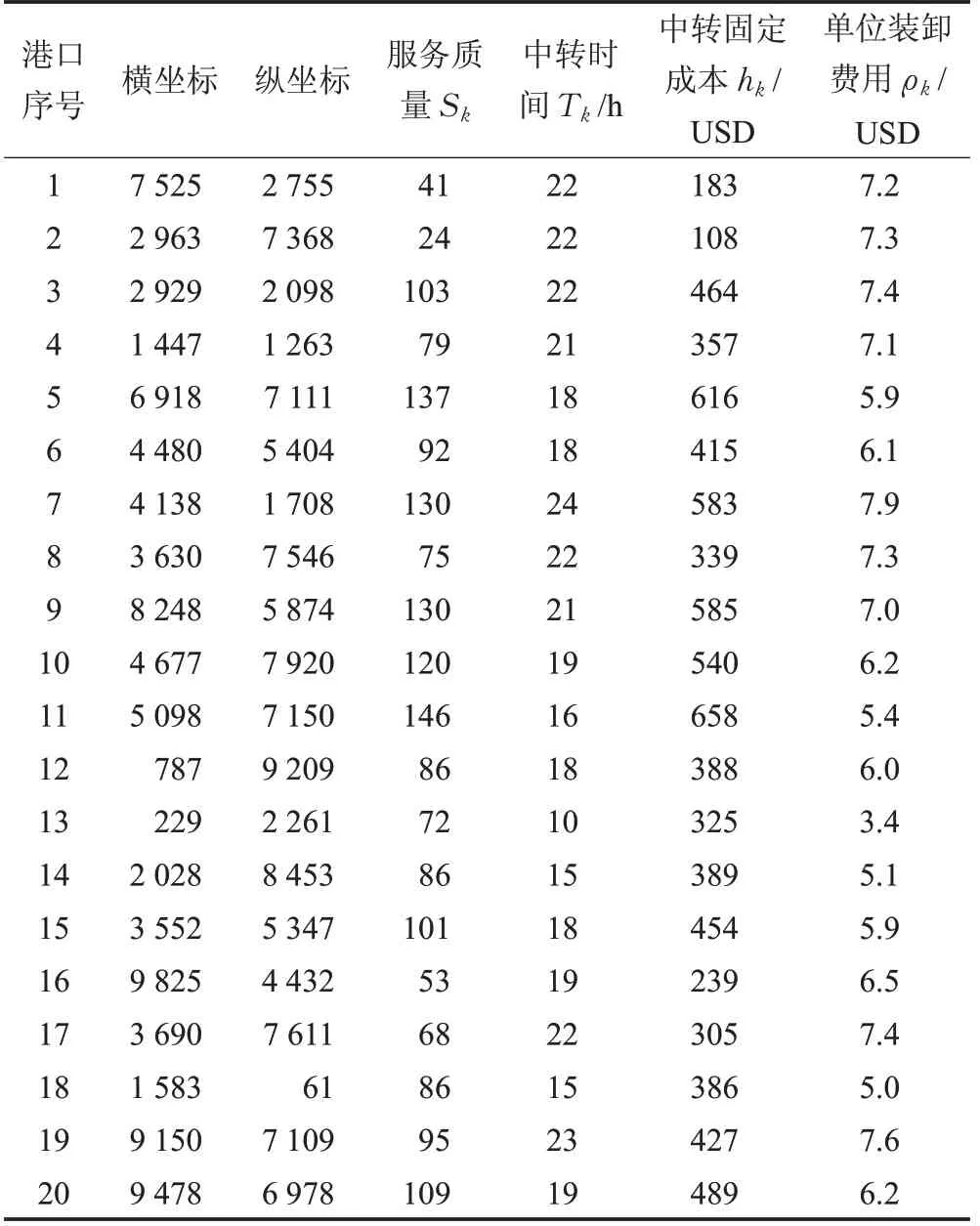
表1 20个港口的相关数据
任意两港口i j 之间的单位集装箱运输价格Pij与单位集装箱运输成本Cij与港口间的直线距离成正相关,并服从正态分布。起讫港口i j 之间的需求(流量矩阵)Qij服从正态分布N(10 000,1 500)。
任意一条航线的吸引力模型的灵敏系数ω=0.75和λ=1.71。碳排放税率为C=22(USD/二氧化碳吨),重油的碳排放因子为β=3.012(二氧化碳吨/燃油吨),集装箱船的速度V =18(knot),集装箱船以速度V =18 航行时单位集装箱重油的消耗量为FV=0.000 39(t/TEU·h)[19]。
4.2 结果分析
4.2.1 海运网络设计结果
在设置枢纽港口的数量为4、规模经济系数α=0.5、权重系数θ=0.5 时,一般的海运网络设计模型M1 求得的枢纽港选址及港口分配方案如图4所示。
在考虑了航线对客户吸引力的影响因素的情况下,枢纽港选址及港口分配如图5所示。
图6为模型M2的遗传算法迭代图。
4.2.2 成本、利润分析
当枢纽港口的数量为4时,模型M1与模型M2分别求得的收入及成本结构如表2所示。
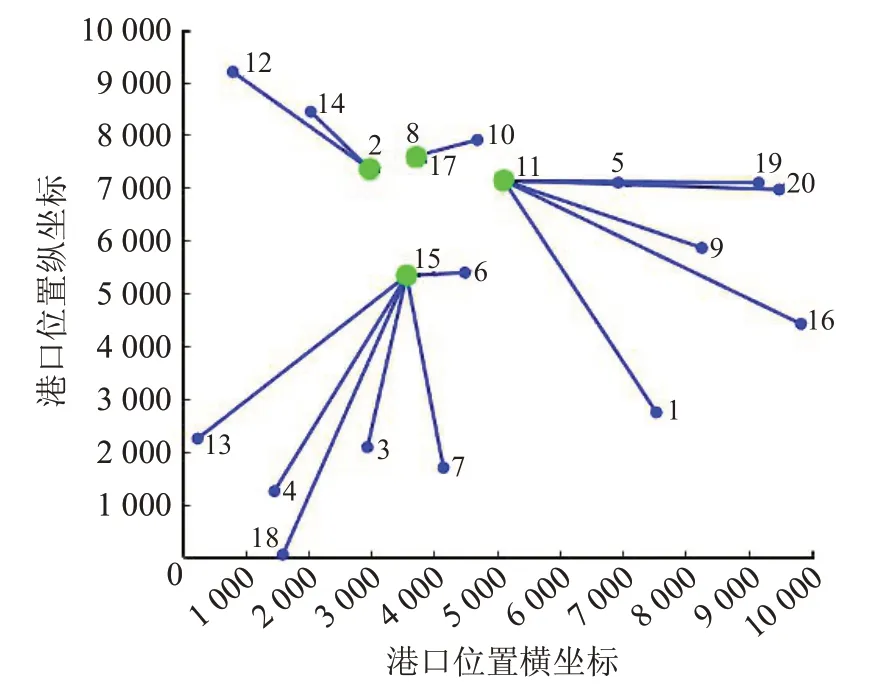
图4 模型M1枢纽港选址及港口分配图
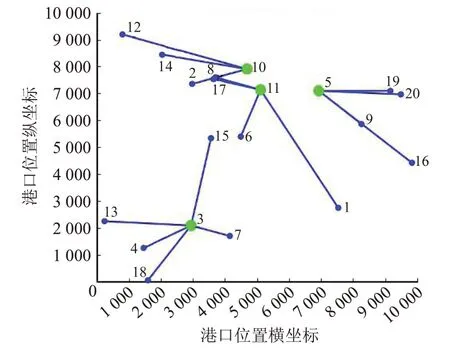
图5 模型M2考虑吸引力的枢纽港选址及港口分配图
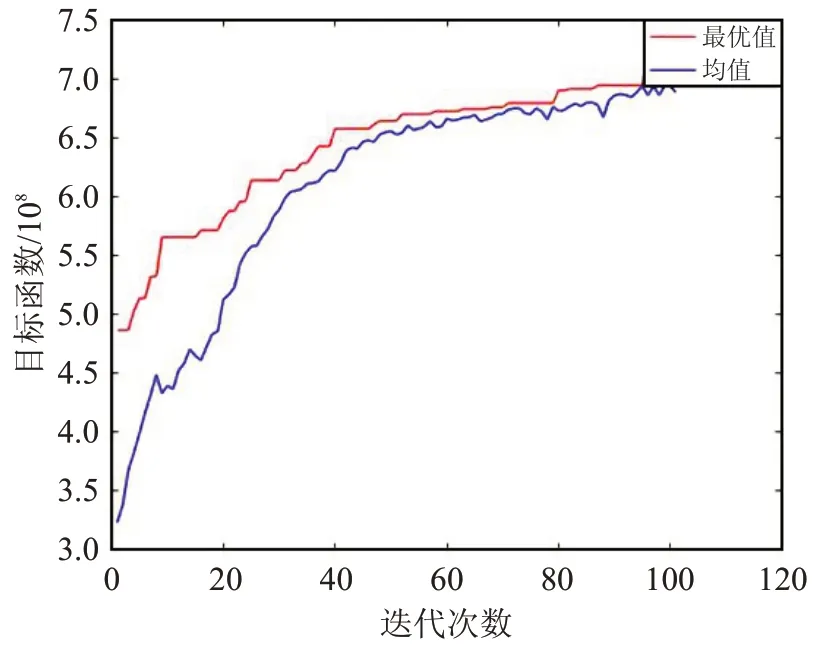
图6 模型M2的遗传算法迭代图

表2 模型M1和M2收入及成本结构108 USD
由表2可知,模型M2求得的利润为7.29×108USD,比模型M1 的结果提高约16%,证明了模型假设的有效性。通过计算可以得知模型M1中各项成本占总成本的比例与模型M2的情况基本相同,即:运输成本约占总成本的83%;中转成本约占总成本10%;环境成本占总成本的7%。航运企业在经营过程中的运输成本占比最大,需重点关注。
通过计算利润与总成本的比值,可以求得航运企业在海运网络经营活动中的利润率。在枢纽港数量不同的情况下,求得的轴辐式海运网络设计方案所对应的利润率如图7所示。

图7 枢纽港口数量不同情况下利润率
通过观察可以发现,无论枢纽港数量是多少,考虑了客户吸引力因素的模型M2 的利润率总是高于模型M1的利润率。而且,随着枢纽港口数量的增加,航运企业获得的利润率呈上升趋势,这是由于枢纽港数量的增加能够产生更多的干线运输航线,有助于规模经济效益的产生。
4.3 模型M1算例分析
为进一步探究航运企业所获得的利润受不同参数设置的影响情况,本文进行多次算例实验。设定港口规模为20个,此时枢纽港口的数量通常为3到5个。在一般模型M1中设置不同数量的枢纽港h、不同的规模经济系数α 进行分析,结果如表3所示。
可初步得到以下结论:规模经济系数α 越大,则航运企业所获利润越低,与现实经验相符。当不考虑枢纽港设置成本时,不同的枢纽港数量下的利润相差不大。航运企业具体所设定的枢纽港数量,要根据当下的规模经济系数来决定。
4.4 模型M2算例分析
在模型M2 的算例结果中,除了规模经济系数α 和枢纽港数量,还要分析权重系数θ 对利润的影响。由上文已知,θ(0 ≤θ ≤1)为关于单位服务价格Pij和服务时间Tklij的权重系数,若θ 的值接近1,则表明客户更重视价格因素;若θ 的值接近0,则表明客户更看重服务时间因素。进行多次算例实验,统计结果如表4所示。
通过分析表4可得出以下结论:
(1)从整体上看,航运企业的利润与规模经济折扣率α 呈负相关的关系。也就是说,规模经济折扣率α 值越小,航运企业的利润越大。
(2)在不同规模经济系数α 情况下,最大利润所对应的枢纽港口数量有所不同。比如,α=0.2 时,设置4个枢纽港获得的利润最大;α=0.6 时,设置3 个枢纽港获得的利润最大。
(3)权重系数θ 与利润存在一定的相关性。当客户对单位服务价格Pij的偏好程度明显高于对单位服务时间的偏好时,航运企业的利润值较低;当客户对单位服务时间的偏好程度明显高于对单位服务价格Pij的偏好时,航运企业的利润值也比较低;当客户对两者的偏好程度相差不多时,所得利润最大。这说明如果客户对所受单位服务价格和单位服务时间的态度比较“极端”(看重一个,轻视另一个)时,不利于航运企业盈利;客户对两者偏好程度较为均衡时,有利于航运企业增加利润。对航运企业的启示是:均衡发展自身提供的单位服务价格与时间,这样可以分散风险,提升所获得的利润。
(4)被选为枢纽港频率最高的港口为3、6、8、9、11等,由港口信息表(表1)可以观察到,这些港口在港口位置、服务质量、效率及中转价格方面具有较大的优势。这说明枢纽港口的选址受到港口综合条件的影响,也从侧面验证了模型的有效性和合理性。
5 结束语
本文研究了航运企业对已有的集装箱轴辐式海运网络的优化问题,突破以往“起讫港口间的货运需求量固定不变”的假设,考虑基于服务约束(服务质量价格时间)的客户吸引力因素对货运需求量的影响,建立了谋求利润最大化的轴辐式海运网络优化问题的两阶段的数学模型。使用遗传算法求解该问题,通过算例验证了模型的有效性。最后,进行了多次仿真实验,分析了不同的枢纽港数量、不同的规模经济折扣率以及托运人对单位服务价格时间的不同偏好程度对航运企业利润的影响。该模型可以对现有海运网络的枢纽港选择和航运线路设计进行优化,并且可以为航运企业提升自身综合服务质量、增加客户吸引力提供参考。

表3 模型M1算例分析
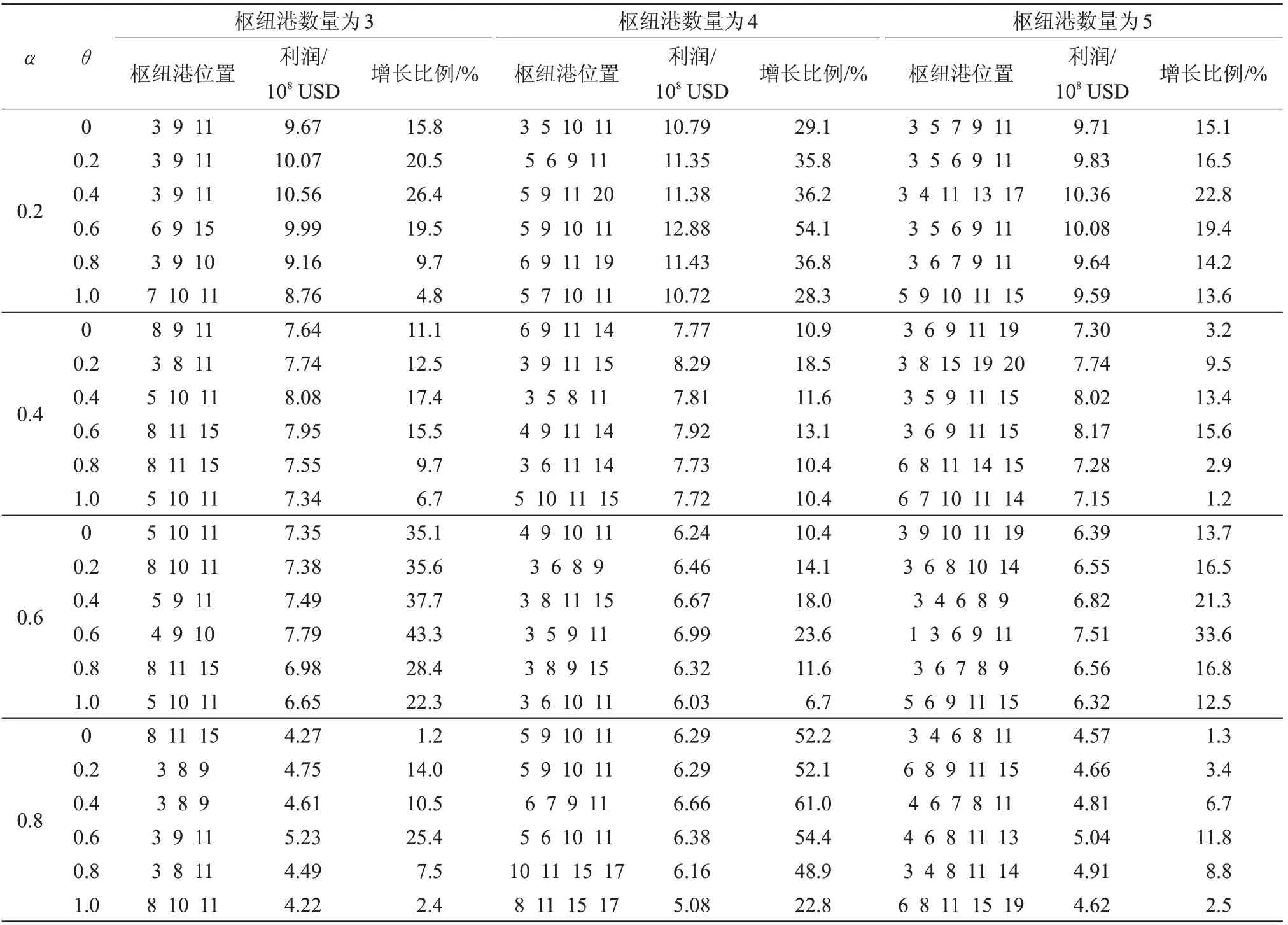
表4 模型M2算例分析
