新型树启发式搜索算法的机器人路径规划

胡晓敏，梁天毅，王明丰，李 敏，2

1.广东工业大学 计算机学院，广州510006

2.广东工业大学 信息工程学院，广州510006

1 引言

移动机器人是智能工业领域的重要辅助工具，代替人类执行危险任务等。其性能主要由三个部分决定：感知外界环境信息的传感器技术[1]、定位和控制机器人位置的GPS 导航技术[2]以及引导机器人智能化作业的智能算法[3]，共同实现移动机器人的路径规划。在该技术中，要解决机器人从某个起始点到某个终止点的最短路径算法求解问题，本文将对路径规划问题中的智能算法进行研究。

现有的路径规划算法主要包含两部分：地图建模和路径搜索算法。算法先对环境信息进行建模，在处理后的地形信息上使用搜索算法。三维空间存在障碍物，建模时常把三维空间栅格化为可行点与不可达的障碍点。已有很多学者提出了两点之间最短路径的规划算法。传统的方法有快速配对算法FM[4]，其效率与空间的总点数相关，运行时间随着空间的点数增多显著增加；混合整数线性规划[5]算法只适用于小规模空间地图；搜索路径较为曲折的A*算法[6]等，这些算法基于贪心选择的方式构建路径。

在复杂障碍物的环境下，移动机器人的路径规划已被证明为NP 难问题[7]。Fu 等人[8]提出量子粒子群优化（QPSO）的方法解决无人机在三维空间规避障碍物的路径规划问题，该空间采用连续的方式建立模型。A*算法作为一种确定性的搜索算法，结合了启发式和最短路径搜索的特点，已被成功应用于各种调度[9-10]、自动驾驶[11-12]、电路配置[13]等问题。Yu等人[14]将A*算法和蚁群算法相结合，利用蚁群算法优化连接三维空间中多个目标点的最短回路，类似求解旅行商问题，然而两个目标点之间的最短路径仍采用A*算法实现。曾有学者提出快速扩展树算法[15]以解决未知连续空间的路径规划问题，但其由于树形结构过于庞大且树节点是随机生成的，在包含狭窄通道的环境中难以搜索到路径，导致得出的最短路径较长。

本文受扩展树结构的启发，对树结构修改成适用于离散已知空间的地图并确定性选出有效点来解决路径规划问题。综合搜索空间压缩和搜索方向引导两方面，本文提出了一种基于可靠边缘点模型的树扩散启发式算法，记为Tree-EP，其创新点包括：

（1）构建可靠边缘点模型，将空间搜索域压缩到可靠边缘点搜索域；

（2）提出树扩散架构选出潜力点以提高引导搜索方向的智能性；

（3）提出潜力点判定范围H ，合适的H 范围设置能增强搜索的导向；

（4）对算法引入局部回溯优化。

实验中测试了Tree-EP算法求解多种带障碍的三维空间路径规划实例的性能，并对比了QPSO 算法，传统A*算法和添加了局部调整操作的改进Tree-EP 算法。实验结果显示，改进Tree-EP具有更佳的路径寻优能力。

2 传统A＊算法

A*算法是路径规划领域里比较流行的启发式搜索算法，该算法的特点是在图G=(V,E)中，从起始点开始，逐步通过探索已知点的邻域以到达终止点，期间在评价已知的路径节点时除了含有当前点到起始点的信息，还添加了到达终止点的启发式信息。评价路径节点的公式为：

其中，f(x)是路径点x 的评估值，g(x)是路径点x 到起始点的距离，h(x)是路径点x 到终止点的启发式距离。算法的运行流程如下：

步骤1 初始化地图所有点的评估值f 为无限大，设置起始点st 的评估值f(st)=0，并将起始点st 放入候选集Q 中。

步骤2 将候选集Q 中评估值f 最小的路径点u 作为下一个路径点，并把该点移出候选集Q。

步骤3 若步骤2 中被移出候选集Q 的点u 为终止点，则结束算法。

步骤4 将点u 邻域里的每一个未加入过候选集Q的点m 加入到Q 中，若g(u)+length(u,m)＜g(m)，则修改g(m)=g(u)+length(u,m)，回到步骤2。

3 空间可靠边缘点模型

传统栅格路径搜索方法搜索所有空间点构建路径解，假设在一个三维空间中，每一维取固定步长分割为n 个点，需对n3个空间点进行搜索，实际上可以筛选出部分空间点以缩小搜索范围。以二维平面为例，如图1，离散后的空间有6 个离散空间点，中间的矩形为障碍物，所围的黑色实心点为障碍点，灰色点为可行点，点A为起始点，点B 为终止点，当点A 和点B 不能直连时，其最短路径的中间点往往经过障碍的边缘附近，如图中的点M 。意味着只需搜索障碍物边缘的位置点。

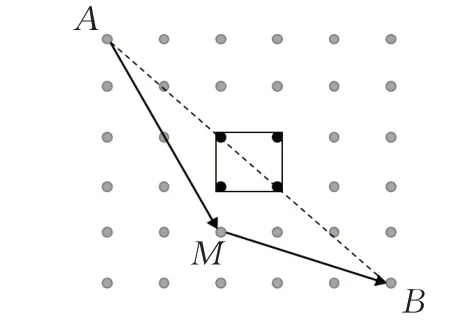
图1 障碍物空间中A、B点之间最短路径

空间可靠边缘点模型的设计思路，就是通过对地图空间中的点进行筛选，根据路径安全情况，筛选出障碍物的可靠边缘点信息。以障碍物周围的可靠边缘点构建路径搜索空间，大大缩小搜索的栅格点数以及调整路径的碰撞风险。

3.1 障碍可靠边缘点构建

本文的方法是构建长宽高分别为lx、ly、lz的三维空间，并对该空间进行等距离的离散化操作，在三维空间中构建O-XYZ 坐标，生成sx×sy×sz个空间点，每个点的坐标值如下：其中sxsysz分别表示每一维上的点密度。通过给定障碍的安全距离δ，得到用于路径构建的障碍周围的可靠边缘点集，该构建步骤为：首先，扩展障碍物周围安全距离δ 内的可行点为非可行点，其余的空间点标记为可行点；其次选出可靠边缘点。对于可行点是否为可靠边缘点的判断方式为：若该可行点周围26 个邻居点里至少存在一个非可行点，则把该可行点定义为可靠边缘点。注意这里的26个邻居点指的是三维空间上当前点(xi,yj,zk)周围的邻居栅格点，坐标分别为(xi+Δx,yj+Δy,zk+Δz)，Δx ∈{-1/sx,0,1/sx}，Δy ∈{-1/sy,0,1/sy}，Δz ∈{-1/sz,0,1/sz}。整个设置过程的伪代码如算法1。

算法1 障碍可靠边缘点构建

For 每一个障碍物

将障碍物所占空间的最小x y z 坐标值各减(δ+1)后标记为min_x,min_y,min_z；

将障碍物所占空间的最大x y z 坐标值各加(δ+1)后标记为max_x,max_y,max_z；

将上述6个更新后的坐标所围空间标记为S；

For 空间S 内的点

If 该点在障碍物周围安全距离δ 内

标记该点为非可行点；

End if

End for

For 空间S 内的可行点

If 该点周围26 个邻居点至少存在一个非可行点把该点定义为可靠边缘点；

End if

End for

End for

3.2 空间两点是否直连的判别方式

空间两点之间的关系可划分为可直连和不可直连。若两点之间的线段不触碰障碍物，则标记这两点为可直连关系；否则，标记为不可直连关系。在判断两点间关系时，对两点间线段上的点进行沿各个坐标轴的等间距抽样，并对抽样后的点归约到离之最近的离散点，若出现任何一个归约后的离散点是不可行点，则判定这两点的连线触碰到了障碍物，并标记这两点的关系为不可直连，实现的伪代码如算法2。

算法2 空间两个可行点P 与Q 的直连关系判断

For 线段PQ 上满足x y 或z 坐标中至少有一个坐标为整数的连续空间点M(x,y,z)

将连续空间点M(x,y,z)归约到与之最近的离散空间点N(x′,y′,z′)；

If 点N 为不可行点

标记点P 和点Q 为不可直连关系；

Break；

End if

End for

If 点P 和点Q 不为不可直连关系

标记点P 和点Q 为可直连关系；

End if

4 基于可靠边缘点模型的Tree-EP算法

4.1 树扩散基本架构

经过空间可靠边缘点模型对空间的压缩后，算法的搜索范围缩小到边缘点上，但对这些边缘点如何排列组合成一条最短路径，需要搜索方向的引导。本文提出树扩散架构的基本思想为：从起始点开始不断扩散探索障碍的边缘，选取出潜力边缘点添加到集合中，直到找到目的点或集合中所有潜力点扩散完毕为止。这里的潜力边缘点必须满足三个要求，分别是：（1）属于边缘点，（2）该点能与扩散点直连，（3）该点判断范围H 内至少存在一个不能与扩散点直连的可行点。

图2 举例说明了选择这些边缘点的原因。图中有三个圆形障碍物，起始点为S，终止点为E。对于起始点S 来说，其扩散的可见边缘点为图中灰色点组成的弧AB，除了点A 和点B 外，弧中的其余点对路径寻优是没有作用的。点A 和点B 除了是点S 的可见边缘点外，还有一个共同特点就是都存在点S 不可直连的可行邻居点。因此满足以上三个要求的边缘点，才值得下一步扩散。

图2 树扩散基本架构

图2 中黑色实心点A B 为点S 扩散的潜力点并被纳入为其孩子节点，点C D 为点A 扩散的潜力点，点F G 为点B 扩散的潜力点，点I 为点G 扩散的潜力点。最后点C D F G I 均能直连终止点，作为树的叶子节点，整个树构建完毕。

4.2 潜力点判断范围H的设置

由树扩散基本架构可知，潜力点的判断影响着整个树形搜索结构。假设有任意潜力点P(x0,y0,z0)，其判断范围H 内的空间点为(x,y,z)，相关设置如下：

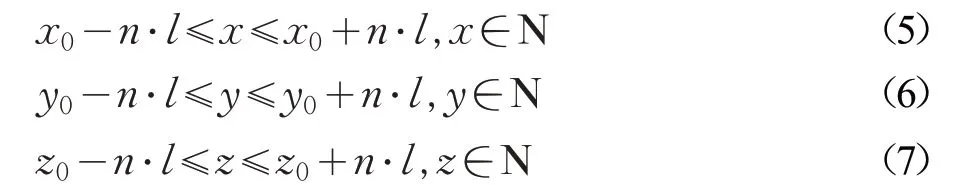
l 为栅格的单位距离，n 为放大的倍数。潜力点判断范围H 如图3所示，H1为n=1 时的范围，H2为n=2 时的范围，n 越大，H 越大，潜力点判断越宽松，得到的潜力点也越多。此处通过图4、图5和图6对比n 在不同设置时被选中的潜力点。图中的黑色矩形为障碍物，黑色实心点为障碍点，点S 为扩散点，空心点为所属点S 的潜力点。可见n=1，2，3时，潜力点的个数分别为3，7和9个，n 越大，潜力点个数越多，也意味着之后需要扩散的点数也越多，树结构越庞大和复杂。为了压缩搜索空间，准确指导搜索方向和精简树扩散架构，本文将n 设置为1。

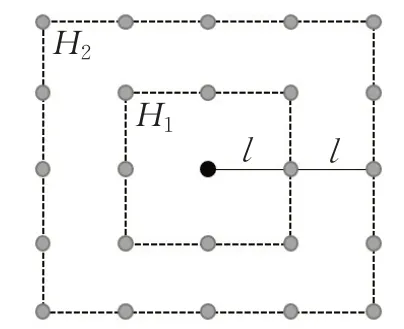
图3 潜力点判断范围H

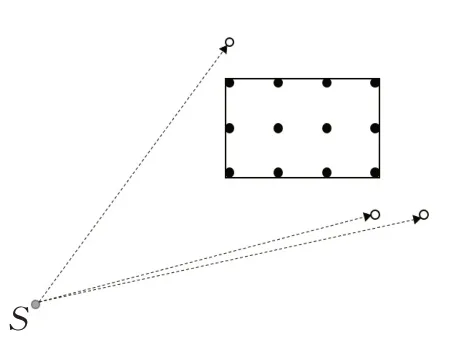
图4 n=1 时的潜力点

图5 n=2 时的潜力点

图6 n=3 时的潜力点

4.3 潜力点扩散机制

Tree-EP 把扩散得到的潜力点纳入候选集，从集合中选出评价值最好的潜力点进行扩散。Tree-EP对每个可行点的评价函数如公式（1），每个潜力点x 的g(x)和h(x)设置为：

cost(x)表示点x 在树结构中不断沿着父节点追踪到根节点的沿途的路径长度。

妊娠期高血压疾病是妊娠期常见并发症之一，主要临床症状为高血压、水肿以及蛋白尿等，如果在发病之初未能及时有效治疗，会导致疾病累及全身器官，甚至造成孕产妇和围生儿的死亡[1-4]。以往硫酸镁是妊娠期高血压疾病的常用首选药物，其能有效缓解微血管痉挛，但降压效果不好[5]。本研究探究拉贝洛尔联合硝苯地平治疗妊娠期高血压疾病的降压效果及临床意义。现将研究结果报道如下。

length(x,ed)表示点x 到终止点ed 的直线距离。Tree-EP的扩散操作伪代码如下所示：

算法3 Tree-EP的扩散操作Extend(x)

If 点x 可以直连终止点

计算点x 的评价值f ；

构建点x 对应的完整路径；

flag=true； //标记已找到最短路

return；

End if

从可靠边缘点集中提取出关于点x 的潜力点集J ；

For 集合J 里的所有潜力点

If 该潜力点已执行扩散操作

continue；

Else

If 该潜力点不在树结构中

把该点作为点x 的孩子节点；

End if

局部回溯优化；

计算该潜力点的评价值f ；

把点x 加入到候选集Q 中；

End if

End for

如图7，引入潜力点扩散机制后，点S 扩散得到点A 和B，均放入扩散候选集Q，发现点A 的评价值比点B 的要小，即评估距离SAE 比SBE 短，于是从集合Q中选出点A 进行扩散，得到点C 和点D，发现点D 的评价值最小，于是从集合Q 中选出D，且发现点D 能直连点E ，输出最短路径SADE 并停止其他节点的扩散。最终整个树架构得到精简，只留下节点SABCD。

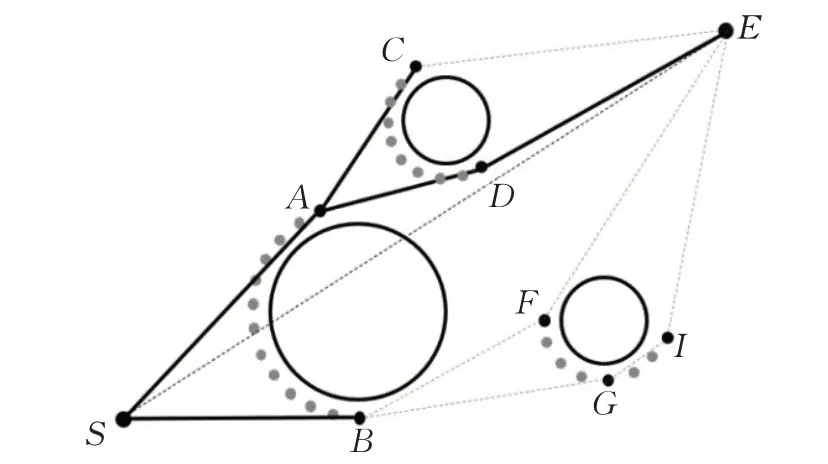
图7 引入潜力点扩散机制的树扩散架构

4.4 局部回溯优化

Tree-EP 在进行搜索时，任意点扩散得到的某个没有孩子节点的潜力点分成两类情况，分别是潜力点不在扩散候选集Q 和已在扩散候选集Q。

4.4.1 潜力点不在候选集Q 时的优化

如果潜力点不在候选集Q，意味着该点不在树中，若该潜力点能与所属扩散点的父节点直连，则在树中将所属扩散点替换成潜力点。如图8，点F 扩散得到点G，点F 的父节点为点E，EF 和FG 的路径长度均为0.3，发现点G 可与F 的父节点E 直连且EG 路径长度0.5 比EFG 的路径长度0.6 要短，把点F 从树中删除，将点G 作为点E 的孩子节点。

图8 潜力点不在候选集Q时的优化

4.4.2 潜力点在候选集Q 时的优化

如果该点沿着新扩散点回溯到根节点的路径长度比沿着父节点回溯到根节点的路径长度要短，则在树中将该潜力点的父节点设为新扩散点。由于该潜力点的父节点变更了，判断该潜力点能否与父节点的父节点直连。如图9，点S 扩散得到A 和B，点A 扩散得到C 和D ，点B 也扩散得到C 和D ，但SBD 的路径长度比SAD 短，因此把点D 的父节点更改为点B。

4.5 Tree-EP的算法流程

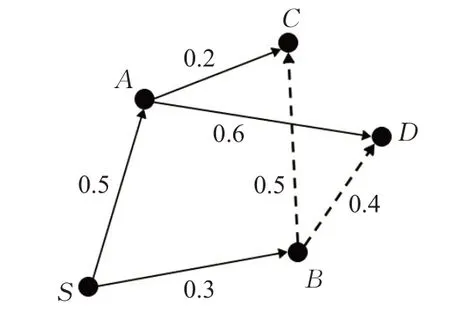
图9 潜力点在候选集Q 时的优化

整体框架如算法4，首先构建地图空间和可靠边缘点模型，然后将起始点纳入到扩散候选集Q 作为初始化，进入循环。从集合Q 中选出评价值f 最小的点x并对该点执行扩散操作extend(x)，扩散完毕后如果找到能与终止点直连的叶子节点，则退出循环，否则继续循环直到候选集Q 为空集。循环结束后输出最短路径。

算法4 Tree-EP

构建地图空间；

构建可靠边缘点模型；

将起始点纳入扩散候选集Q；

While 扩散候选集Q 不为空

从扩散候选集Q 中选出评价值f 最小的点x；

Extend(x)；

If flag==true

Break； //已找到最短路径

End if

End while

输出最短路径

4.6 Tree-EP与A＊的搜索过程对比

在两点之间求解最短路径的路径规划问题中，A*算法的路径搜索方向是依靠空间点到终止点的启发式数值和到起始点的实际路径距离引导的，其扩散过程是不断将邻居点纳入候选集，再不断从候选集中选出评价最好的点进行路径构建引导算法进行搜索。尽管A*的整体搜索方向总是指向终止点，如果指向终止点的方向有障碍物阻挡，各条路径会在触碰到障碍之后才改变方向继续构建路径，这种预测性不强和碰到阻碍才改变搜索方向的缺陷使得A*算法构建出来的路径较长。A*算法的搜索过程中纳入大量的邻居点，没有充分利用空间中的障碍信息。

本文提出的Tree-EP算法根据受障碍阻挡的两点间最短路径往往触碰障碍物边缘的原则，设计出利用潜力边缘点进行最短路径构建的扩散机制，扩散得到的潜力点纳入候选集，从集合中选出评价值最好的潜力点进行扩散。这种方法利用了障碍边缘信息，把路径搜索直接指向最有潜力扩散的边缘点，提前规划避开障碍物的搜索方向，能带有预测性地引导路径的构建。图10 举例比较了两种算法的搜索过程。

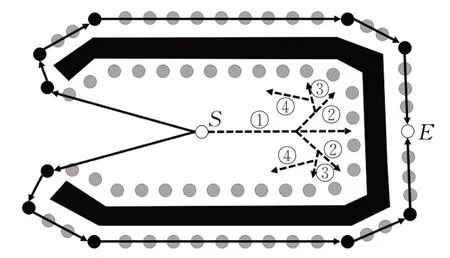
图10 Tree-EP和A*的搜索过程

图10 中点S 为起始点，点E 为终止点，黑色实心多边形为障碍物，灰色点为Tree-EP搜索时忽略的点，黑色实心点为树结构中的节点，也即潜力点，黑色带箭头的实线表示扩散过程，带箭头的虚线表示A*的搜索方向，旁边的标号代表A*搜索方向的变化。对于A*算法，根据其特性会先往直线SE 方向搜索，即方向①，然后触碰墙壁后，搜索方向稍微往SE的垂直方向靠近，再次触碰墙壁后继续调整搜索方向，直到找到搜索的出口，其在障碍物包围区域里的搜索方向按编号①②③④的顺序变化，可见A*算法要经历多次搜索才找到障碍物包围空间的出口。而Tree-EP 算法先提取出障碍边缘点，在扩散过程中判断图中的灰色点均是无意义点，逐步将潜力点构建到树结构中，最后得出最短路径。图中的黑色带箭头的实线表示Tree-EP的搜索方向，可见比A*算法的搜索要更加准确。

Tree-EP 在进行边缘点确认的过程中，其判定对象是空间中障碍物周围的边缘点，基于空间中的障碍位置进行潜力边缘点的选择，目前激光测距、声呐探测的技术都为障碍位置的判定提供了方法，无需对全图的空间点进行分析判断。

5 实验设计及数据分析

5.1 测试用例

本文选取了圆形、矩形和山脉三类障碍物作为用例。为了便于比较，本实验中三个坐标轴的栅格密度都取相同值。圆形和矩形实例相当于在三维空间上有圆柱和矩形柱的障碍，把起始点与目标点的z 坐标都设置为0，该三维实例转换为二维表示。这两个实例用于比较不同形状的障碍边缘对算法寻找最优路径的影响。圆形和矩形实例在密度为20下的障碍位置如表1和表2所示。其中表1 显示该实例有11 个障碍，属性中的(x,y,r)分别代表障碍的圆心和半径值，在圆形内的空间都属于障碍物。

表1 圆形实例的障碍设置（密度20）

表2 矩形实例的障碍设置（密度20）

表2 给出了矩形实例的障碍位置数据，共有9 个矩形柱障碍，其中表中的属性数据(x,y,lx,ly)表示该矩形在密度为20下的左下角x 和y 坐标，lx和ly表示矩形在该坐标下往x 轴和y 轴正方向的长和宽度值。

本文在不同栅格密度下的圆形和矩形实例都是通过对表1 和表2 中的坐标数据进行缩放获得的。山脉实例采用远大于栅格密度数量的随机点插值出地形高度的方式生成三维地形。因此本实验能反映出不同栅格密度下，算法对同一个三维带障碍空间的路径搜索能力。

圆形和矩形实例的起始点和目标点的坐标都分别取值为（0，0）和(sx-1,sy-1)，山脉实例的起始点和目标点的x 和y 坐标取值同上，而z 坐标则取对应位置的地形高度以及安全距离之和以上的栅格点高度。每类障碍物在不同密度下的总像素点数和边缘点数如表3到表5 所示。从表中看到，构建障碍可靠边缘点过程后，搜索的潜在空间点数大大减少。

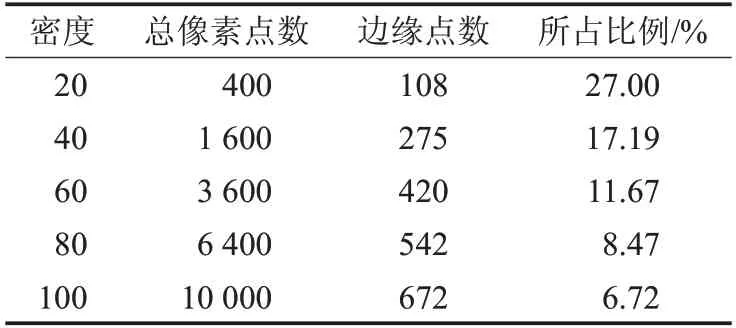
表3 圆形实例

表4 矩形实例

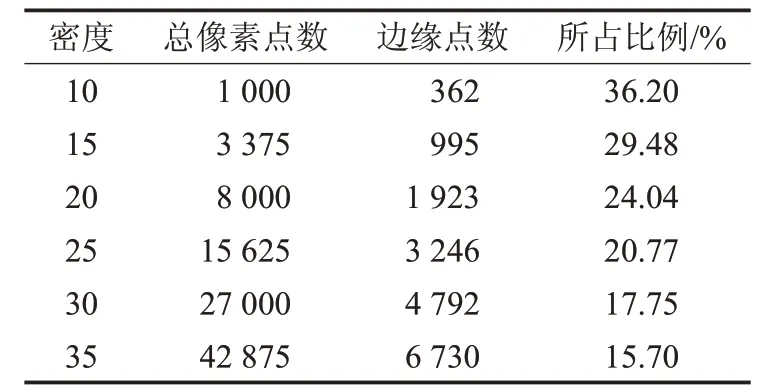
表5 山脉实例

边缘点数所占空间总点数的比例随着密度的上升而下降。特别是在栅格密度增大的情况下，比如每一维都为所测最大密度时，边缘点的数量在三个实例中只有原始空间总点数的5.72%～15.7%。

5.2 算法设置与数据表示

本文比较了量子粒子群优化（QPSO）[8]、传统A*、添加了局部调整操作的改进A*、Tree-EP 和改进Tree-EP这五种算法对最短路径求解的性能。其中QPSO 为群体智能优化算法，用于对比不同算法的路径寻优能力，其参数设置与文献[8]一致，本实验给出的数据均为QPSO在30次独立运行中的最优解。

为了比较不同密度值对最优路径长度的影响，实验结果中对路径长度进行了归一化：首先，把三维空间栅格化后，每个栅格的步长为1，得到一个新的栅格坐标；然后，通过算法搜索出最优路径，计算栅格空间中路径点之间的欧几里德距离，得到该最短路径的长度；第三，把路径长度值除以密度值，得到去除密度值影响的归一化后的路径长度值。

5.3 不同栅格密度下路径长度的比较

表6 比较了五种算法对圆形实例的标准化路径长度值。从表中可以看到，QPSO在全部所测密度下的路径长度比A*的要好，在密度为20以外时的结果比Tree-EP和改进Tree-EP要差。全部算法当中，结果最差的是A*算法，但是经过局部回溯优化后的改进A*比A*的结果好很多，说明A*算法在路径构建时过于粗糙，其自身有很大的优化空间。但是经过改进后的A*算法性能仍比Tree-EP和改进Tree-EP都要差，说明加入树扩散架构的Tree-EP 和改进Tree-EP 的路径搜索性能得到了质的提高。

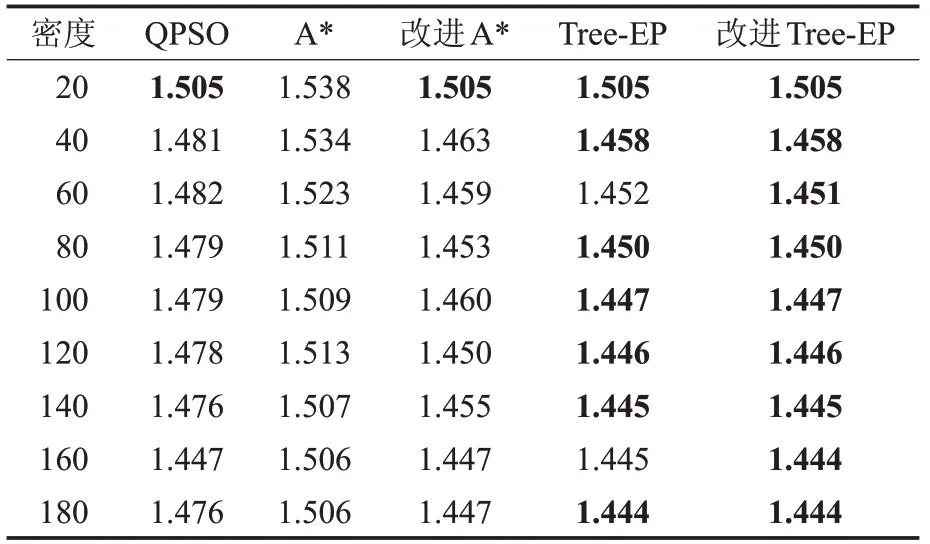
表6 各算法标准化路径长度的比较（圆形实例）

从表7 给出的矩形实例的测试结果可知，Tree-EP和改进Tree-EP 同样表现出优越的性能，在各个密度的路径长度都比QPSO、A*和改进A*的好。

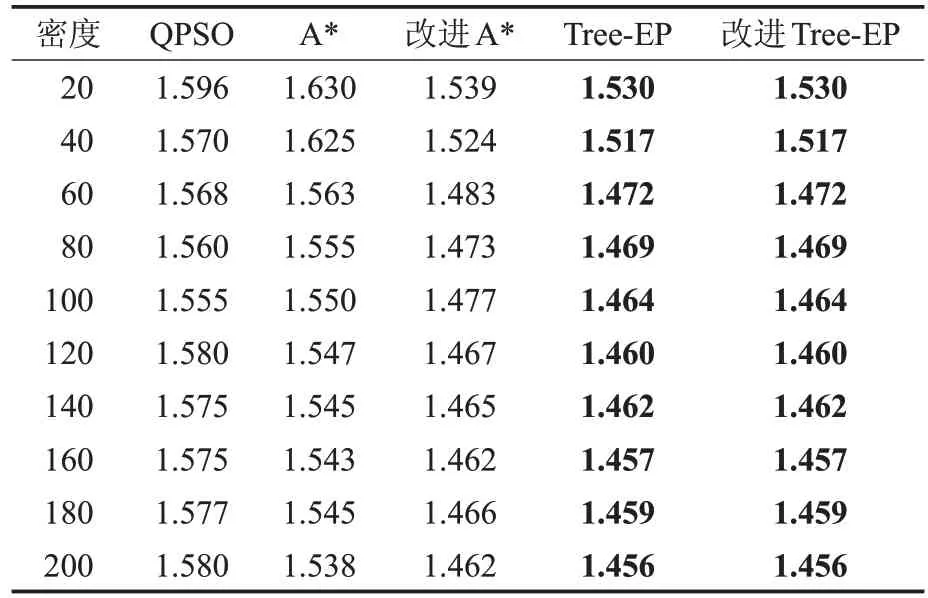
表7 各算法标准化路径长度的比较（矩形实例）

对于地形细节较多和较复杂的三维山脉实例，如表8在相同密度比较下，QPSO的路径均比A*的要好，但比改进A*、Tree-EP 和改进Tree-EP 要差。A*算法在引入局部回溯优化后的改进A*结果比原来要好，在Tree-EP中加入该优化操作后的改进Tree-EP 也得到更好的结果，说明了局部回溯优化在复杂和崎岖的地形下效果显著。

表8 各算法标准化路径长度的比较（山脉实例）

5.4 栅格密度影响的进一步分析

空间的栅格密度影响算法最终得到的最短路径。由于Tree-EP 和A*算法都是基于空间栅格进行路径构建，栅格点密度过小会导致位于障碍之间的最优路径被忽略。图11比较了算法在圆形实例栅格密度为20和40得到的最优路线。图中实心点代表该栅格点是不可行点。当密度为20 时，过小的密度导致算法忽略了中间障碍密集的区域，当栅格密度增大到40 时算法才发现障碍间的更优路径。因此，栅格密度的下限值应与空间中任意两个障碍之间扣除两边安全距离后得到的最小距离有关。

另一方面，从表7 的数据看出，增大栅格密度有可能提高算法找到更优路线的能力，但由于存在舍入误差，并不保证算法可以得到更短的路径长度。例如，密度为180 时得到的长度比密度为160 时要长。图12 比较了算法在矩形实例栅格密度为60 和180 时的路径图。可见当密度增大后，在保证安全距离前提下路径更贴近障碍，路径长度更短，而且Tree-EP算法总能找到比其他算法更短的路线。

对于山脉实例来说，得到的最短路径值随着栅格密度增大呈递减的趋势。图13对比了算法在栅格密度为15 和45 的路线图。栅格密度增大后，栅格空间表现的空间高度差异更加细化，改善了障碍之间部分的最优路径被忽略的问题。然而空间密度的增大会增加搜索空间的点数量，延长运算时间。从表8 的结果看出，栅格密度取值为45 和50 时改进的Tree-EP 算法得到的标准化路径长度的改善程度已经小于0.5×10-3，是否加大栅格密度取决于实际问题的精度需要。

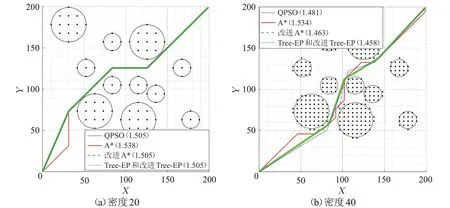
图11 圆形实例下密度为20和40的路径图示

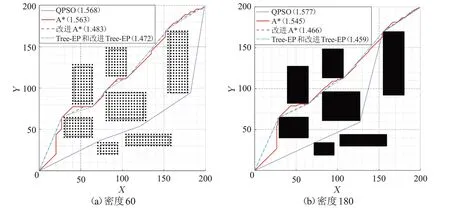
图12 矩形实例下密度为60和180的路径图示

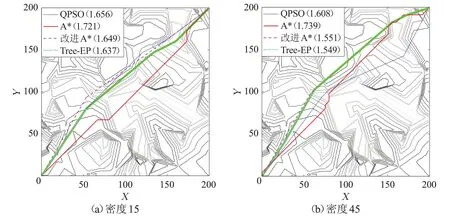
图13 山脉实例下密度为15和45的等高线图

6 结束语

本文提出了一种用于缩小搜索空间的可靠边缘点模型，能将整个空间压缩到边缘点搜索空间，在此基础上再提出树扩散架构，该架构从边缘点中提取出能有效指导搜索方向的潜力点。另外将潜力边缘点搜索机制和树扩散架构相结合，提出了Tree-EP算法，该算法能搜索出空间中的有效路径点，最终得出更好的最短路径。此外，还对算法引入局部调整策略得到新型的改进Tree-EP 算法，结果显示该优化机制有局部修正路径的功能，能进一步缩短所得路径的长度。实验对QPSO、A*、改进A*、Tree-EP 和改进Tree-EP 的性能进行比较，总的来说，Tree-EP和改进Tree-EP的最短路径搜索性能很好，对两点间最短路径搜索的路径规划问题有着重要的意义。