改进果蝇算法优化CIAO-LSTM网络的时序预测模型

李 春，高 飞，王会青

太原理工大学 信息与计算机学院，太原030024

1 引言

时间序列是指某种现象或某一类统计指标按照时间的先后顺序排列形成的序列。时间序列已经存在于生活的各个领域中，如洪水预报[1]、天气预报[2]、能源消耗[3]等。利用时间序列的历史信息以及数据之间的相关性进行假设与推理，为科学决策提供了理论及实践支持。时间序列预测一直是各个领域研究的热点问题之一。

时间序列受到各方面因素影响，通常表现为非线性、非平稳性、快速变换且包含噪声等特点。为了提高时间序列预测的精度，各个领域学者提出了不同的时间序列预测方法。自回归滑动平均模型（ARIMA）[4]是一种传统的线性时间序列预测模型，但ARIMA 主要针对平稳时间序列，具有较大的局限性。大数据时代的到来，传统的线性时序模型已经不能解决高度非线性的时间序列问题。随着人工智能的发展，神经网络这类新的非线性时间序列预测模型已经广泛应用于各个领域。Huang W[5]和Lv Y[6]等人将深度信念网络（DBN）用于当前短期交通预测中。李哲敏等人[7]采用动态混沌神经网络用于农产品价格预测。龙勇等人[8]采用反向传播神经网络（BPNN）用于电力负荷预测。但是，这些网络由于其拓扑结构特点无法捕获长时间的序列依赖关系进而降低了预测的准确度。

循环神经网络（Recurrent Neural Network，RNN）是一种可以感知上一时刻信息的定向循环神经网络，可以很好地处理输入数据之间关联的问题[9]，因此RNN相比其他神经网络更适合用于时间序列预测。但是，RNN随着时间间隔的增加会丧失学习多个间隔之前信息的能力，最终导致梯度消失或爆炸。Sak H等人[10]针对RNN的不足提出了长短期记忆神经网络（Long Short-Term Memory，LSTM），该网络通过使用“门”结构不仅具有了长期记忆的能力，还解决了梯度消失或爆炸的问题。所以，LSTM近几年已经广泛应用于各个领域[11-12]。

Alkhasawneh M S 等人指出神经网络在处理目标系统包含线性成份时精确度不高[13]。针对高度非线性的神经网络可能会忽略线性因素的影响，本文提出了将多个时间步的输入与输出进行全连接的LSTM 网络（CIAO-LSTM），增强了网络的泛化能力与预测精度。同时，针对BPTT复杂度高、易收敛于局部最优的缺点，本文通过改进的果蝇优化算法（IFOA）优化网络参数，提高了网络优化能力。

2 相关工作

2.1 长短期记忆网络（LSTM）

传统的人工神经网络认为数据之间是独立的，而没有考虑数据之间的时序性，所以对于时间序列数据并不能很好地拟合。长短期记忆网络（LSTM）作为一种特殊的循环神经网络（RNN），不仅具有RNN 对前面信息进行长时记忆的特点，还通过增加遗忘门避免长期依赖的问题。在LSTM 细胞结构中，包括遗忘门ft、输入门it、输出门Ot和1个记忆单元，其内部结构如图1所示。

遗忘门决定了保留多少上一时刻的单元状态Ct-1信息在当前状态Ct中，计算公式为：

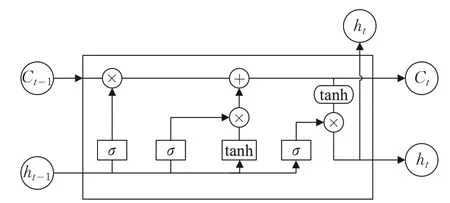
图1 LSTM细胞结构示意图

输入门控制新信息的输入，计算公式为：

更新记忆单元状态为：

输出门计算公式为：

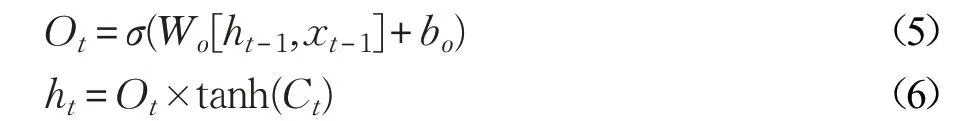
输出层计算公式为：

虽然LSTM在时间序列研究中取得了一定的成果，但是当目标系统中包含线性关系且含有噪声时，高度非线性的LSTM网络会造成训练模型过拟合，降低时序预测的精度。同时，LSTM参数在反向调节所采用的BPTT（Back Propagation Through Time）算法存在复杂度高、容易收敛于局部最优等缺点。

2.2 果蝇优化算法（FOA）

果蝇优化算法（FOA）由我国学者潘文超先生[14]提出，是基于果蝇觅食行为寻求全局最优的新方法。果蝇优化算法可应用于求解全局最优解，FOA算法可归结为以下几个步骤：

步骤1 初始化果蝇群体最大迭代次数Maxgen 和种群规模Sizepop ，随机初始果蝇群体位置(X_axis,Y_axis)。

步骤2 赋予果蝇个体利用嗅觉搜寻食物的随机距离与方向，R 为果蝇搜索半径。

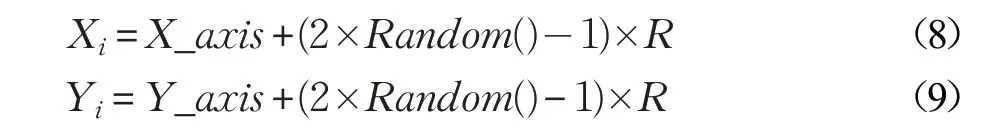
步骤3 由于无法得知食物的位置，因此通过判断与原点的距离Di，并且以距离的倒数作为味道浓度的判定值Si。

步骤4 通过将浓度判定值Si代入浓度判定函数f()中求出果蝇个体的味道浓度，并找出该果蝇群体味道浓度最高（最低）的果蝇。

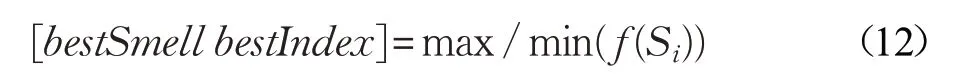
步骤5 保留最佳味道浓度值与X 、Y 坐标，此时果蝇群体利用视觉向该位置飞去。

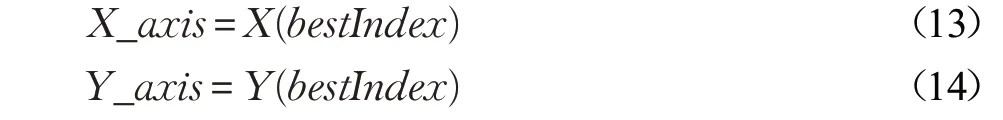
步骤6 重复执行步骤2～4，若当前味道浓度优于前一迭代味道浓度，则执行式（12），直到达到迭代次数Maxgen 为止。

3 基于改进果蝇算法优化CIAO-LSTM网络的时序预测方法

3.1 直连长短期记忆神经网络（CIAO-LSTM）

时间序列分为线性时间序列和非线性时间序列两类，在以往的时间序列预测研究中，大部分学者首先通过一定手段判断时序数据的性质，然后选择合适的模型。即使在非线性的时序数据中也可能包含线性关系，当目标系统中包含线性关系且含有噪声时，高度非线性的LSTM网络可能会造成训练模型过拟合，降低时序预测的精度。针对这种问题，本文提出了改进的CIAOLSTM（Connect Inputs and Outputs in Long Short-Term Memory）网络，即直连长短期记忆网络。通过将时间序列中的每个时间步输入与预测输出进行全连接，从而加强了整个网络对于时序数据中的线性关系描述，提高了网络的泛化能力。本文针对时序数据进行滚动预测，即多个时间步输入预测多个输出。改进后的CIAO-LSTM网络的拓扑结构如图2所示。

图2 CIAO-LSTM网络结构拓扑图

图2 中，{X0,X1,…,Xt-1}是多个时间步的输入值，{Yt,Yt+1,…,Yt+n} 是多个时间步的预测输出值，Ct、Ct+1是当前LSTM 细胞的输出状态，{W0t,W(t-1)t} 、{W0t+1,W(t-1)t+1}代表多个时间步输入值与预测输出值连接权重。预测输出值Yt的表达式如式（15）所示：

3.2 改进的果蝇优化算法（IFOA）

传统FOA算法在步骤2中，果蝇个体在搜寻食物时以固定的半径R 向四周随机搜索。搜索半径R 的大小与算法性能直接相关，搜索半径较大时可以在前期具有较强的全局寻优能力，但后期会造成局部收敛较慢的问题，而搜索半径过小则可能会陷入局部最优。

文献[15]提出了改进的DS-FOA 算法，该算法中搜索半径R 满足以下函数关系式：

其中，变量Rmax为初始最大搜索半径，常量Iter 为当前迭代次数，常量Itermax为初始最大迭代次数。

在DS-FOA 算法中，搜索半径在初期下降较为迅速，极易陷入局部最优。本文基于DS-FOA做出了改进的果蝇优化算法，在迭代前期采用最大搜索半径提高全局寻优能力，而在迭代后期通过对搜索半径采用衰减策略使其能够收敛于局部最优点。改进之后的搜索半径定义如式（17）所示：

其中，μ 是搜索半径的衰减因子。

改进后的式（16）只是增加了全局寻优能力，而寻优的收敛速度并没有得到解决。文献[16]针对式（11）适应度函数进行了修正，使得FOA 算法可以在有限的迭代次数和极小的搜索半径内取得全局最优解，修正后的适应度函数如式（18）：

式中，Δ 为逃脱系数，可以使适应度函数取得负值。

采用改进后的式（17）与式（18）相结合提出的IFOA算法，不仅可以解决目标函数寻求全局最优的问题，而且可以加快寻优的收敛速度。

3.3 IFOA算法优化CIAO-LSTM网络

传统的LSTM 通过BPTT 算法（Back Propagation Through Time）对参数进行优化，但BPTT 存在复杂度高、容易收敛于局部最优等缺点。本文将IFOA 算法用于优化CIAO-LSTM网络（IFOA_CIAO-LSTM算法），在保证模型能够收敛于全局最优的同时，减小了寻优的迭代次数。IFOA_CIAO-LSTM算法流程如图3所示。

IFOA_CIAO-LSTM算法具体过程如下：

步骤1 确定CIAO-LSTM网络的拓扑结构。

步骤2 初始化最大迭代次数、果蝇种群规模，每个果蝇包含网络初始连接的权重与偏置。由于在一个固定时间步长的权重与偏置共享，故输入到LSTM细胞的权重与偏置只需要初始化一次，果蝇初始位置为(X_axis,Y_axis)。

步骤3 赋予果蝇个体利用嗅觉搜寻食物的随机距离与方向，R 为果蝇搜索半径。

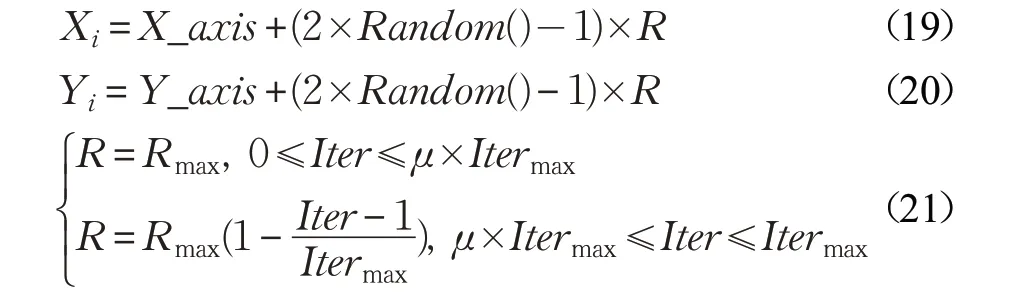
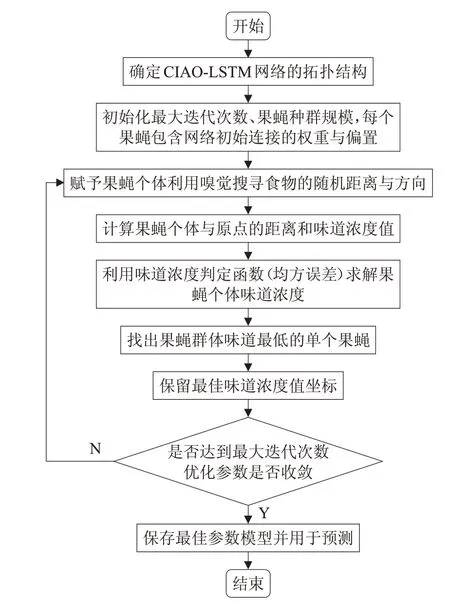
图3 IFOA_CIAO-LSTM算法流程图

步骤4 判断与原点的距离Di，并且以距离的倒数作为味道浓度的判定值Si：

步骤5 通过浓度判定函数中求解果蝇个体的味道浓度，本文将CIAO-LSTM 网络均方误差（Mean-Square Error，MSE）作为浓度判定函数。

式中，y'是预测输出值，y 是真实值。

步骤6 通过将浓度判定值Si代入浓度判定函数f()中求出果蝇个体的味道浓度，并找出该果蝇群体味道浓度最高（最低）的果蝇。

步骤7 保留最佳味道浓度值与X 、Y 坐标，此时果蝇群体利用视觉向该位置飞去。

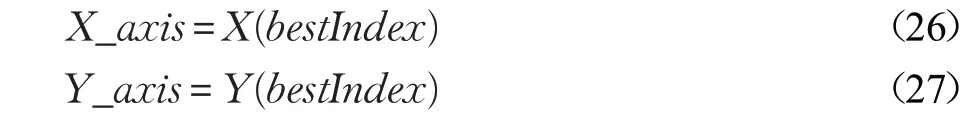
步骤8 重复执行步骤3～7，若当前味道浓度优于前一迭代味道浓度，则执行步骤6，直到达到迭代次数Maxgen 为止。最后将保留的最佳参数模型保存并进行预测，输出预测结果。

4 实验结果与分析

4.1 实验环境与数据

实验环境为python3.5，tensorflow1.7.0 框架，ubuntu16.0.4，8 GB 内 存，Inter®Core ™，i7-3632QM CPU@2.2 GHz。

本实验选取了四组不同领域的时间序列数据来测试模型的适用性及性能，第一组来自澳大利亚能源市场运营商（Australian Energy Market Operator，AEMO）提供的新南威尔士州2017 年的全年电力负荷数据，第二组至第四组数据来自DataMarket 提供的1965—1980 年二氧化碳浓度、1962—1975 年牛奶产量数据和1990—2015 年股票当日交易最高价。其具体的数据信息如表1所示。

表1 数据集信息

4.2 数据预处理

为了提高模型预测精度，对数据进行归一化处理，通过公式（28）将数据映射到[0，1]范围之间，xt为实际值，xt' 为归一化后的值，xmax与xmin为数据集中的最大与最小值。得

到的预测输出值按公式（29）反归一化为实际值，yt'为归一化的网络输出预测值，yt是网络输出反归一化后的实际值。

4.3 实验评价标准

为了评价IFOA_CIAO-LSTM预测方法的性能。主要通过以下两个指标评价该方法性能：（1）不同预测模型的预测序列与实际序列的拟合效果对比图；（2）归一化均方根误差（normalized Root Mean Square Error，nRMSE）和平均绝对百分误差（Mean Absolute Percentage Error，MAPE）作为评价指标，定义如下：

其中，y' 表示网络输出的预测值，y 表示实际值，ymax是测试数据的最大值，ymin是测试数据的最小值，N 表示测试数据的长度。

4.4 实验结果与分析

实验1 不同时序模型的预测曲线与实际曲线拟合效果对比。

本文分别采用长短期记忆（LSTM）网络模型、直连长短期记忆（CIAO-LSTM）网络模型、基于果蝇算法优化直连长短期记忆网络（FOA_CIAO-LSTM）、基于改进果蝇优化算法的直连长短期记忆（IFOA_CIAO-LSTM）网络模型设计预测实验。将这四种模型分别应用在四组不同领域的时序数据上，对不同模型的预测结果与实际结果进行对比，并通过拟合曲线图来评价不同模型的优劣。第一组和第四组数据由于测试集较大，因此选取了部分数据体现数据的拟合程度。

图4 为四种预测模型在四组数据上的预测值与实际值拟合图。从图中可以看出，CIAO-LSTM 模型对不同时序数据的拟合效果优于传统的LSTM 模型，表明LSTM 加入输入与输出全连接加强了时序数据的拟合效果，因此该网络相比传统的LSTM具有更高的预测精度。FOA_CIAO-LSTM模型拟合效果优于CIAO-LSTM模型，表明果蝇优化算法在寻找最优网络参数能力优于传统BPTT 算法。图4（d）中，LSTM 模型、CIAO-LSTM模型和FOA_CIAO-LSTM 模型在峰值具有较大的偏差，拟合效果较差。而IFOA_CIAO-LSTM 模型采用寻求全局最优和快速局部收敛的改进果蝇优化算法，克服了传统BPTT算法陷入局部最优的问题，在峰值可以更好拟合，表明改进的果蝇算法（IFOA）相比传统的FOA算法具有更强的全局寻优能力。同时，IFOA_CIAO-LSTM模型相比本文其他模型对于波动较大的数据可以更好地拟合。

实验2 各模型在不同数据集下归一化均方根误差（nRMSE）、平均绝对百分误差和模型训练时间对比结果。

从表2中的第4、5列可以得出，CIAO-LSTM模型的nRMSE和MAPE明显低于LSTM模型，表明CIAO-LSTM模型相比传统的LSTM模型，在时序预测方面有更好的预测精度。由表2中的第3、6列可以得出，CIAO-LSTM模型在传统的LSTM 模型加入输入与输出全连接可以降低模型隐藏层神经元个数，进而加快了模型的训练时间。

同时，IFOA_CIAO-LSTM的nRMSE明显低于其他三种模型，表明采用改进的果蝇优化算法（IFOA）提高了网络的寻优能力，进而提高了模型的预测精度，因此IFOA_CIAO-LSTM 网络模型在时序预测方面具有更好的性能，且IFOA_CIAO-LSTM 模型在不同数据集下的MAPE 均在3%以内，在实际应用中具有一定的指导作用。

根据以上实验可以得出，本文提出的IFOA_CIAOLSTM模型与本文其他模型相比，在不同数据集上具有较强的泛化能力和较高的预测精度，且对于波动较大的数据也可以进行很好的拟合，是一种高效的时间序列预测模型。

5 结束语

图4 不同模型预测值与真实值拟合效果图

表2 不同数据集下四种模型的实验结果

为了提高时间序列的预测精度，本文提出了一种基于改进果蝇算法优化CIAO-LSTM 网络参数的时序预测方法。首先通过将长短期记忆网络的多个时间步输入与输出进行全连接（CIAO-LSTM），解决了目标系统包含线性成分时预测精确度不高的问题。其次，利用改进的果蝇优化算法（IFOA）对CIAO-LSTM 网络的参数进行优化，解决了传统BPTT算法优化网络易陷入局部最优解的问题。同时，本文提出的IFOA_CIAO-LSTM在时序预测方面具有较高的预测精度，对波动较大的数据也可以很好地拟合，因此该模型在实际应用中可以发挥重要的作用。下一步将探究本文提出的网络模型与优化参数方法是否在文本处理、语音识别等其他领域仍然具有优势。