基于LBSN动态异构网络的时间感知兴趣点推荐

李 全，许新华，刘兴红，林 松

湖北师范大学 教育信息与技术学院，湖北 黄石435002

1 引言

随着移动设备和全球定位系统（GPS）的快速发展，人们日常使用的智能终端提供的位置定位功能越来越精确。在此背景下，基于位置的社交网络（Location-Based Social Network，LBSN）服务得到迅速的发展，且受到了广大用户的喜爱，如国外比较主流的Gowalla、Yelp和Facebook Places等，国内比较主流的嘀咕和街旁等[1]。相对于传统的社交网络，LBSN 优势在于用户能够以签到的形式发布他们的地理签到信息，并对已访问的兴趣点（Point-Of-Interest，POI），例如咖啡厅、餐馆和电影院等，与朋友分享他们的体验和经验。在一个城市里可能包含成千上万的兴趣点，但用户可能只想访问它们的一小部分。因此兴趣点推荐的任务就是帮助用户推荐新的感兴趣的位置[2]。

相对于传统推荐系统，兴趣点推荐系统的发展更加复杂。首先在基于位置的社交网络中用户访问兴趣点只占非常小的比例，兴趣点推荐面临数据稀疏性问题。然后用户通常喜欢访问当前所在位置附近的兴趣点。最后随着不同的时间，用户的兴趣是动态变化的。例如，在日常生活中，有些人喜欢中午喝咖啡，有些人喜欢晚上去酒吧等。因此兴趣点推荐系统应该考虑位置影响、社会关系和时间影响等上下文信息[3-4]。基于以上考虑，本文提出了一种基于LBSN 动态异构网络的时间感知兴趣点推荐算法。本文的主要贡献如下：首先在LBSN异构网络模式中增加了会话节点类型，通过动态元路径，在用户和兴趣点语义关系之间有效融入时间信息、位置信息和社交信息等。其次设置了用户-兴趣点之间的元路径集，并提出了不同动态元路径对应的路径实例偏好度的计算方法。然后采用矩阵分解模型对不同动态偏好矩阵进行矩阵分解。最后根据不同动态元路径对应的用户特征矩阵和兴趣点特征矩阵，获取用户在不同的时间访问兴趣点的top-k 推荐列表，从而有效地丰富数据，解决数据稀疏性问题，提高兴趣点推荐的实时性和准确性。

2 相关技术

协同过滤推荐系统包括基于邻域协同过滤和基于模型协同过滤。基于邻域协同过滤又可以分为基于用户（User-based）协同过滤和基于项目（Item-based）协同过滤，但它们通常面临着冷启动、数据稀疏、算法可扩展性差等问题[5]。随着基于位置社交网络的快速发展，兴趣点推荐可为人们提供更好的基于位置的服务，受到学术界和工业界的广泛关注。基于协同过滤的推荐技术被应用到兴趣点推荐中。由于兴趣点推荐的签到数据具有高稀疏性，因此基于协同过滤方法很容易遭受数据稀疏问题。当前许多研究试图利用并融合地理影响和社会影响等来提高兴趣点推荐的效果。

在融合社交信息方面：Zhang 等[6]将用户间的相似性关系嵌入到基于用户的协同过滤技术中；Ye等[7]利用用户社交网络中好友的协同评分以及通过距离衡量好友之间的相似性来进行兴趣点推荐。在融合地理位置信息方面：Lian 等[8]提出一种结合地理影响的加权矩阵分解方法；Hu等[9]基于非负矩阵分解模型融合用户的兴趣类别和地理位置信息进行兴趣点推荐，采用用户的邻居影响因素对地理位置信息进行建模。在融合社交信息和地理位置信息方面：Ye等[10]关于兴趣点推荐采用线性插值的方法结合地理与社会影响应用到基于用户的协同过滤框架中；Cheng等[11]将用户社交关系和地理位置融入概率矩阵分解模型。通过建立用户在位置上的签到概率模型作为多中心高斯模型来捕获地理影响力，继而把社交信息和地理信息融入到一个概率的矩阵分解模型中。以上方法都是从融合社交信息和地理信息的角度解决兴趣点推荐数据稀疏问题，但用户的兴趣在不用的时间是动态变化的，因此它们忽略了时间信息。

现有的基于时间感知的兴趣点推荐系统主要将时间划分为若干个时间间隙，并根据时隙将用户签到信息进行划分，最后融入时间信息和其他信息实现基于协同过滤的兴趣点推荐。例如：Gao 等[12]提出了融合时间影响的兴趣点推荐模型。该模型通过矩阵分解方法获取某时隙的用户潜在特征矩阵和位置潜在特征矩阵，最后将所有时隙的用户潜在特征矩阵作为正则化项实现时间感知的兴趣点推荐。Yuan 等[13]提出了一个名为UTE-SE的时间感知兴趣点推荐模型。计算不同时隙签到点的相似度，并采用平滑技术对签到矩阵进行处理，解决数据稀疏问题。最后将时间信息和位置信息融入到基于用户协同过滤推荐中。以上基于时间感知的兴趣点推荐方法考虑了时间信息和地理信息，但它们的可扩展性较差，在解决数据稀疏方面无法融合更多丰富的信息。

为了更好地解决签到数据稀疏和用户兴趣动态变化等问题，本文提出了一种基于LBSN动态异构网络的时间感知兴趣点推荐算法。该算法优势在于：

（1）在LBSN 异构网络中增加时间感知层，定义会话节点的重要度，通过参数使得与目标时间强相关的会话节点增加，并且与目标时间越近的会话节点具有更大的权重，从而提高了兴趣点推荐的实时性和准确性。

（2）设置了用户-兴趣点之间的动态元路径集。在此基础上，通过计算动态路径实例的偏好度构造用户-兴趣点动态偏好矩阵，从而有效融入时间信息、位置信息和社交信息，缓解兴趣点推荐中数据稀疏问题。

（3）提出了一种基于LBSN动态异构网络的兴趣点推荐算法，对不同动态偏好矩阵进行矩阵分解，根据不同动态元路径的用户特征矩阵和兴趣点特征矩阵，获取用户在目标时间访问兴趣点的推荐列表，从而实现更加人性化的兴趣点推荐任务。

3 问题定义

3.1 LBSN动态异构网络

异构网络是指由不同类型节点的集合和不同类型边的集合构成的有向图。基于位置社交网络是一种典型异构信息网络。由于用户签到偏好是动态变化的，因此为了表示用户在不同时间签到偏好，在LBSN异构信息网络中加入会话节点，其定义如下。

定义1（LBSN动态异构网络）LBSN动态异构网络被定义为四元组G ＜Us,Ss,Ls,Es＞，其中Us表示网络中所有用户节点的集合，其中Us={u1,u2,…,un} 。 Ss表示网络中所有会话节点的集合，其中Ss={sij|1 ≤i ≤n,1 ≤j ≤24}。Ls表示网络中所有兴趣点节点的集合，其中Ls={l1,l2,…,lm}。Es表示网络中所有边的集合，其中Es=EUU⋃EUS⋃ESL⋃ELL。EUU={(ui,uj)|ui,uj∈Us}表示用户ui和用户uj之间的好友关系，EUS={(ui,sij)|ui∈Us,sij∈Ss}表示用户ui在时间tj有签到行为，ESL={(sij,lk,)|sij∈Ss,lk∈Ls}表示用户ui在时间tj访问兴趣点lk，ELL={(li,lj)|li,lj∈Ls}表示兴趣点li和兴趣点lj之间的位置关系。LBSN动态异构网络如图1所示。

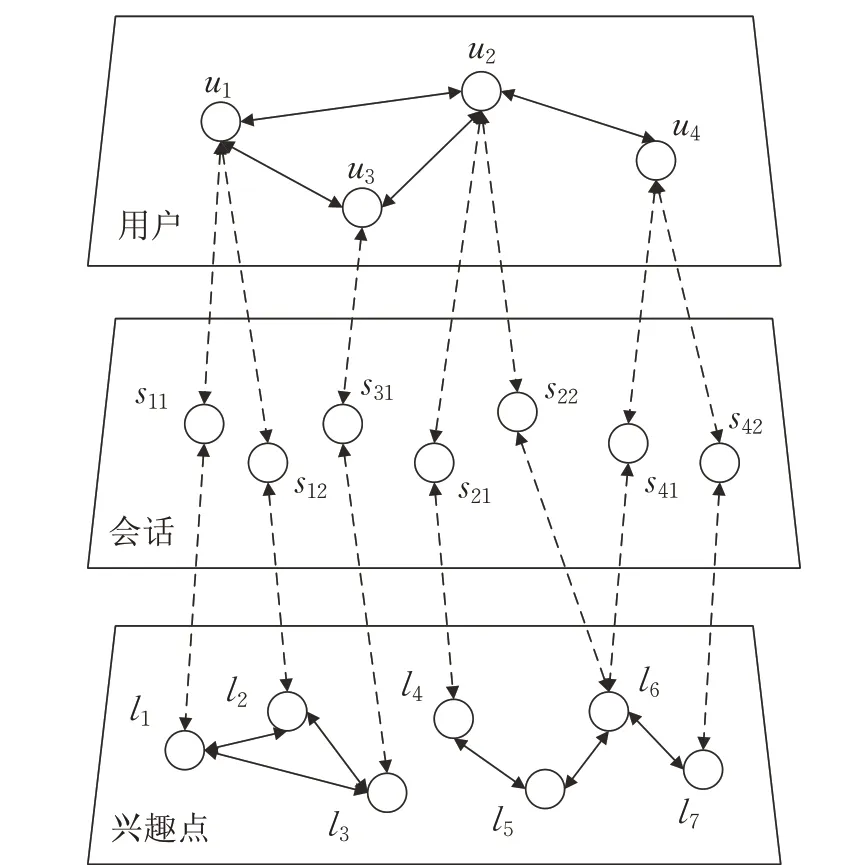
图1 LBSN动态异构网络图

3.2 LBSN动态网络模式

网络模式概念类似于数据库中E-R图，它是由不同实体型和联系类型构成的有向图，其定义如下。

定义2（LBSN动态网络模式）LBSN动态网络模式被定义为四元组G ＜U,S,L,R ＞，其中U 表示用户节点类型，S 表示会话节点类型，L 表示兴趣点节点类型。联系类型为R={RUU,RUS,RSL,RLL}，其中RUU表示用户之间的好友关系，RUS表示用户与时间之间的会话关系。 RSL表示用户在某时间和兴趣点的签到关系。RLL表示兴趣点之间的位置关系。LBSN动态网络模式如图2所示。

图2 LBSN动态网络模式图

3.3 LBSN动态元路径与路径实例

元路径用来描述网络模式中两类对象之间的连接路径[14]。不同的元路径代表了对象类型之间可以通过不同节点类型和联系类型建立不同的语义关系。LBSN动态元路径和动态路径实例定义如下。

定义3（LBSN动态元路径）在LBSN动态网络模式G ＜U,S,L,R ＞中，LBSN 动态元路径定义为如下形式：

定义4（LBSN动态路径实例）在LBSN动态异构网络G ＜Us,Ss,Ls,Es＞中，对于元路径An，若存在真实的路径p=(v1,v2,…,vn)，其中，vi∈{Us,Ss,Ls}，vi和vi+1之间的类型为Es。那么动态路径p称为动态元路径P 的一条动态路径实例。

例如，在LBSN 动态网络模式G ＜U,S,L,R ＞中存在一条动态元路径U →S →L →L。该元路径表示用户可能喜欢与某个时间访问过的兴趣点位置相关的兴趣点。该动态元路径对应的动态路径实例如图3所示。

图3 动态路径实例图

4 基于LBSN动态异构网络兴趣点推荐

4.1 LBSN动态元路径集

基于LBSN动态网络模式，确定起始于用户节点类型且终止于兴趣点节点类型的元路径集。已有大量研究表明[15-16]，相距3 度之内的是强连接，超过则为弱连接，通常研究长度在3 以内的路径。但考虑LBSN 中时间信息对兴趣点推荐的实时性以及签到数据的稀疏性，结合实际情况，本文的动态元路径集包括2 条3 度以内的元路径和3条4度以内的元路径，具体如表1所示。

表1 用户-兴趣点之间动态元路径集表

4.2 基于LBSN动态元路径的偏好度计算

已知LBSN 动态异构网络G ＜Us,Ss,Ls,Es＞，则在目标时间td，以v1(v1∈Us)为起点、vn(vn∈Ls)为终点的基于动态元路径P 的偏好度为该元路径对应的动态实例路径集P′偏好度之和，计算公式如公式（1）所示：

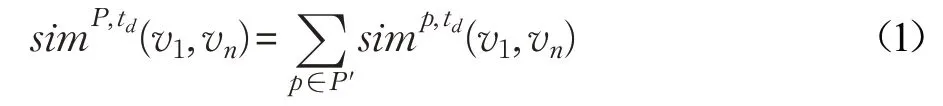
其中，simp,td(v1,vn)表示在目标时间td基于动态实例路径p 得到的用户和兴趣点之间偏好度。simp,td(v1,vn)=，其中为动态实例路径p 中节点vi和节点vi+1边的权重。LBSN动态异构网络一共有4种类型边的权重，分别为WUU、WUS、WSL和WLL，其中WUU={wui,uj|(ui,uj)∈EUU}表示用户和用户边的权值集合，WUS={wui,sij|(ui,sij)∈EUS} 表示用户和会话边的权值集合，WSL={wsij,lk|(sij,lk)∈ESL}表示会话和兴趣点边的权值集合，WLL={wli,lj|(li,lj)∈ELL}表示兴趣点和兴趣点边的权值集合。异构网络中边权值有计数计量、二值计量和对数计量等方法，其中二值表示权值一般获得较好的推荐结果。因此，对于用户与用户边，如果用户之间存在好友关系，则权值均为1，否则为0。对于会话与兴趣点边，如果用户于某时间在兴趣点有过签到行为，则权值均为1，否则为0。但是，为了更好地反映用户兴趣变化的时间属性和兴趣点的距离属性，用户和会话边的权值及兴趣点和兴趣点边的权值采用如下方法确定。

4.2.1 用户和会话边的权值

时间感知兴趣点推荐的任务是为目标用户ui在目标时间td推荐其感兴趣的兴趣点。由文献[17]可知，当用户ui在时间tj有签到行为时，与目标时间td越近的会话节点对推荐任务就越重要。因此，将会话节点的重要度定义如公式（2）所示，并将用户和会话边的权值设置为会话节点的重要度，即wuisij( )tj,td=f( )tj,td。

其中，H 是一个控制会话节点时间影响度的参数。当|tj-td|≤12 时，两个时间的距离为 |tj-td|；当 |tj-td|＞12 时，两个时间的距离为24- ||tj-td。

4.2.2 兴趣点和兴趣点边的权值

用户一般喜欢访问距离较近的兴趣点。本文采用如下方法确定用户从一个位置转移到另一个位置的偏好度。首先获取位置之间的空间距离样本Y ，如公式（3）所示[18]：

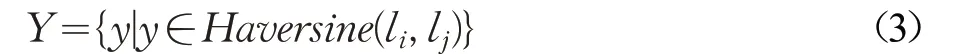
其中li，lj为两个位置的经度和纬度坐标，Haversine 是一个空间距离函数，用于计算两个位置之间的空间距离。然后，采用距离dis(dis ∈Y)的幂律函数表示位置转移的偏好度，如公式（4）所示：

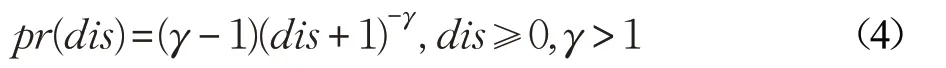
其中，γ 是幂律函数的参数，它可以通过公式（5）得到：

本文将兴趣点间边的权值设置为位置转移的偏好度，且wlilj=pr(dis)。

4.3 基于动态元路径的兴趣点推荐

在LBSN 动态异构网络G ＜Us,Ss,Ls,Es＞中，已知动态元路径Pk∈{P1,P2,P3,P4,P5}和目标时间td，构造用户-兴趣点动态偏好矩阵MPk,td，该矩阵的元素MPk,td(i,j)表示用户ui∈Us和兴趣点lj∈Ls在元路径Pk下所有路径实例的权重之和，且MPk,td(i,j)=simPk,td(ui,lj)。五个元路径对应的动态偏好矩阵分别为MP1,td，MP2,td，MP3,td，MP4,td，MP5,td。采用矩阵分解模型对每一个动态偏好矩阵进行矩阵分解，得到五组用户特征矩阵和签到点特征矩阵，分别为UP1,td，LP1,td，UP2,td，LP2,td，UP3,td，LP3,td，UP4,td，LP4,td，UP5,td，LP5,td。因此，用户ui在目标时间td访问兴趣点lj的预测偏好度，其中θk为第k 条元路径的权重。为第k 组用户特征矩阵的用户ui的特征向量，为第k 组签到点特征矩阵的兴趣点lj的特征向量。在此基础上，将预测偏好值最高的前N 个兴趣点作为推荐结果。

4.4 算法描述

基于LBSN 动态异构网络的兴趣点推荐算法（PRDHN）步骤如下：

输入：动态异构网络G ＜Us,Ss,Ls,Es＞，动态元路径M={P1,P2,P3,P4,P5}，用户ui，目标时间td。

输出：兴趣点推荐结果LR。

1. for each meta-path Pk∈M do

2. Pk′=findInstancePathSet(Pk)

3. for each instance-path p ∈P′do

4. simPk,td(u,l)+=simp,td(u,l)，u ∈Us，l ∈Ls

5. end for

6. Generate MPk,tdbased on Pk

7. end for

8. for each matrix MPk,td，Pk∈M do

9. Decompose MPk,tdto UPk,tdand LPk,td

10.end for

11.Lc=initializeCandidateSet(ui)

12.for each lj∈Lcdo

14.end for

15.LR=TOP-N(Lc)

假设LBSN动态异构网络G ＜Us,Ss,Ls,Es＞有n 个用户，r 兴趣点，m 条边。第1步的for循环时间复杂度为O(c)，c 为元路径集的大小。第3 步的for 循环时间复杂度为O(m) 。第8 步的for 循环时间复杂度为O(c)。第9 步对每个元路径对应的矩阵进行分解的主要开销主要来自于目标函数E 和对应的梯度下降函数。目标函数的时间复杂度为O(ntˉk)，其中tˉ表示用户的平均签到数量，k 表示特征向量的维度。梯度下降函数的时间复杂度为。第12 步的时间复杂度为O(r)。所以该算法的总时间复杂度是O(cm+cntˉk+r)。因为c 为常数5，且ntˉk ≫m,r ，所以O(cm+cntˉk+r)≈O(ntˉk)。由文献[12]可知，典型的LRT时间感知兴趣点推荐算法时间复杂度为O(nrk)。因为tˉ＜r，所以PRDHN算法的时间复杂度小于LRT算法。

5 实验设计与分析

5.1 数据集

本文选择了两种公开签到数据集进行算法测试，分别为Gowalla 和Brightkite。这两个数据集都同时包含了用户信息、兴趣点信息、签到信息和时间信息等。首先对两个数据集进行预处理。把一天24小时划分为24个时隙，将数据的时间信息取整划分到24 个时隙中。将每个数据集70%的数据作为训练集，剩余30%的数据作为测试集。两个数据集统计特性如表2所示。

表2 数据集统计特性表

5.2 评价标准

为了评价兴趣点推荐算法的性能，本文使用准确率（Precision@N）和召回率（Recall@N）作为评价指标，其中N 表示兴趣点推荐的个数。准确率指推荐结果中用户将来真正去的数量占推荐总数的比例。召回率指推荐结果中用户将来真正去的数量占用户将来访问兴趣点总数的比例。用户进行兴趣点推荐的准确率和召回率定义如公式（6）所示：

其中，R(u)为对用户u 进行推荐的兴趣点集合，T(u)为用户u 在测试集上实际的签到集合。

5.3 实验结果分析

为了验证基于LBSN 动态异构网络的兴趣点推荐算法的推荐效果，将它与7种兴趣点推荐算法进行比较和分析。各对比算法介绍如表3所示。

表3 兴趣点推荐算法对比表

实验1 会话参数H 对准确率和召回率的影响

在两个数据集中，通过调整会话节点参数H 分析本文会话节点对推荐算法准确率和召回率的影响。在进行推荐TOP-5 兴趣点实验中，会话节点参数H 对准确率（Precision@5）和召回率（Recall@5）的影响如图4所示。

由图4 可知，当1 ≤H ≤2 时，两个数据集准确率和召回率都比较低，因为较小的H 值使得与目标时间强相关的会话节点减少，从而产生了数据稀疏问题。当3 ≤H ≤4 时，两个数据集的推荐效果最好，因为较大的H 值使得与目标时间强相关的会话节点增加，并且与目标时间越近的会话节点具有更大的权重，从而验证了会话节点对推荐性能的影响。当5 ≤H ≤8 时，两个数据集准确率和召回率逐渐降低，因为随着H 值的继续增加，导致了时间信息对推荐系统的影响降低。

实验2 基于时间感知兴趣点推荐算法的实验分析

人们的生活一般都具有规律性，即他们在特定的时间喜欢去感兴趣的位置活动。因此时间信息影响着兴趣点推荐算法推荐结果的实时性。该部分实验在两个数据集的基础上分别测试了5 种推荐算法的准确率和召回率，实验结果如图5所示。

由图5 可知，在基于协同过滤的兴趣点推荐算法中，User-based CF和MF CF算法在进行兴趣点推荐时没有考虑时间信息，因此它们的兴趣点推荐效果最差。在进行推荐TOP-5兴趣点实验中，LRT和UTE算法相对于User-based CF算法在两个数据集的准确率上提高了43%～55%。它们相对于MF CF算法在两个数据集的准确率上提高了32%～45%。此结果表明，时间感知的兴趣点推荐算法可以提高推荐系统的准确率和召回率。本文PRDHN 算法相对于LRT 和UTE 算法在两个数据集的准确率上平均提高了8%～15%。因为基于动态异构网络PRDHN算法在融入时间信息的同时又融入位置信息和社交信息等，进一步地提高时间感知兴趣点推荐算法的推荐精度。

实验3 融合情景的兴趣点推荐算法实验分析

由于兴趣点推荐系统中签到数据非常稀疏，因此融合情景信息有助于提高兴趣点推荐算法的准确率和召回率。该部分实验在两个数据集的基础上分别测试了4 种融合情景的兴趣点推荐算法，实验结果如图6所示。

图4 会话参数H 对准确率和召回率的影响

图5 基于时间感知兴趣点推荐算法对比图

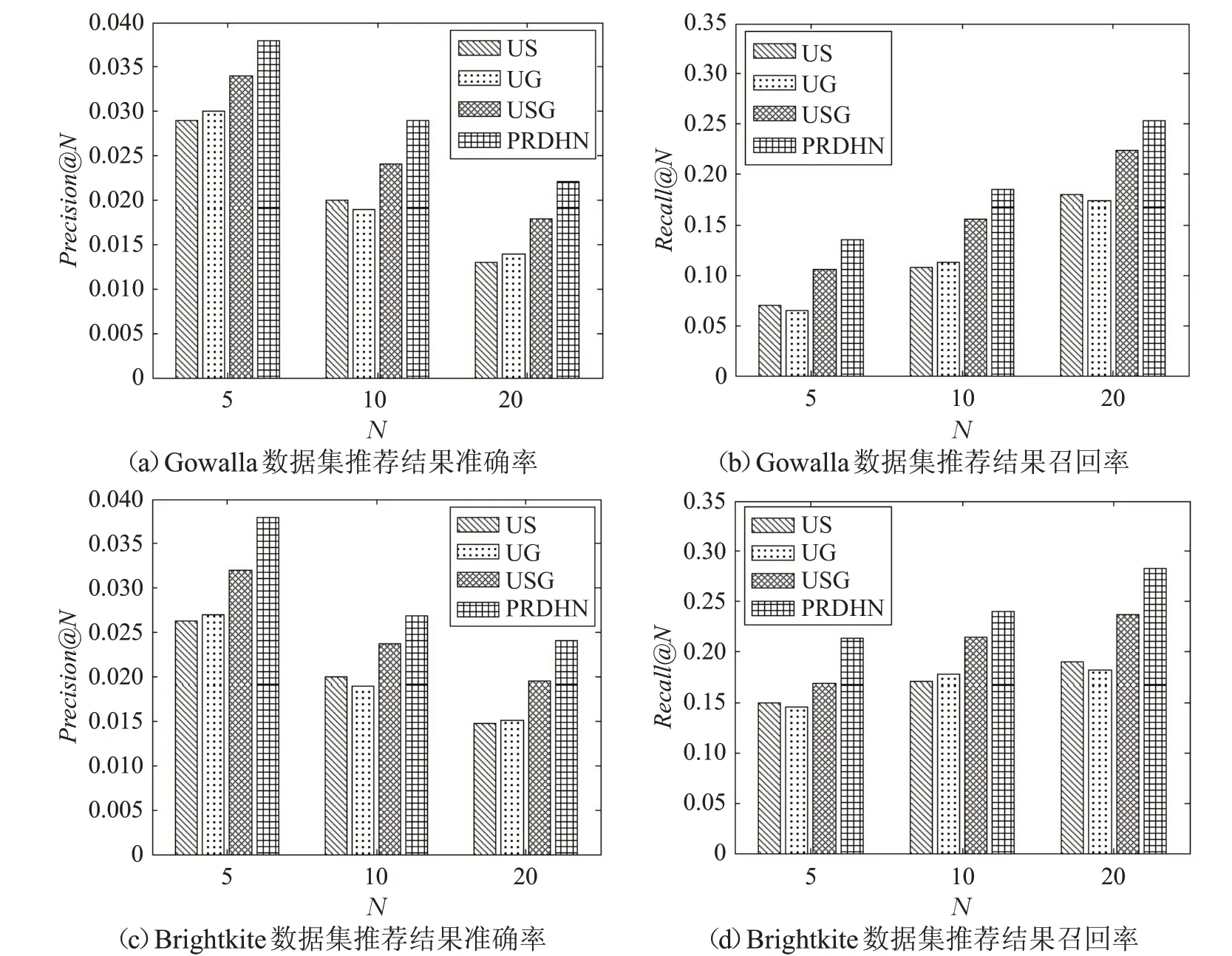
图6 融合情景的兴趣点推荐算法对比图

由图6可知，US和UG在进行兴趣点推荐时分别只融合了社会信息及地理信息，因此它们的兴趣点推荐效果最差。在进行推荐TOP-5 兴趣点实验中，USG 算法相对于US 算法和UG 算法在Gowalla 数据集上的准确率分别提高了17.2%和13.3%，同理在Brightkite 数据集上的准确率分别提高了23.1%和18.5%。本文PRDHN算法相对于USG算法在两个数据集的准确率分别提高了11.7%和18.7%。因此该方法的兴趣点推荐效果最好。实验结果表明，以LBSN 动态异构网络为基础，融合地理位置、社会关系和用户偏好的时间感知的兴趣点推荐算法可以进一步地提高推荐系统的推荐精度和召回率。

6 结束语

针对基于位置社交网络提出了一种基于LBSN 动态异构网络的时间感知兴趣点推荐算法。首先在LBSN异构网络模式中增加了会话节点类型，并通过动态元路径，在用户和兴趣点之间语义关系中融入时间信息、位置信息和社交信息。其次设置了用户-兴趣点之间的动态元路径集，并提出了动态路径实例偏好度的计算方法。然后采用矩阵分解模型对不同动态偏好矩阵进行矩阵分解。最后结合不同动态元路径对应的用户特征矩阵和兴趣点特征矩阵，获取用户在不同的目标时间访问兴趣点的top-k 推荐列表。实验结果表明本文算法的精确度相比其他相关的兴趣点推荐技术有了较好的提高。在未来的工作中，将在推荐系统中融入文本信息等其他信息，并通过神经网络和表示学习技术，进一步提高兴趣点推荐的性能。