双叉式叶尖结构对风力发电机叶片固有频率影响的试验研究*

□ 代元军 □ 贺 凯 □ 翟明成

1.新疆农业大学 机电工程学院 乌鲁木齐 8300012.上海电机学院 机械学院 上海 2013063.新疆工程学院 能源工程学院 乌鲁木齐 8300014.新疆工程学院 能源高效利用技术重点实验室 乌鲁木齐 830001

1 研究背景

随着传统能源的过度消耗,人们对新能源越来越重视。风能具有可持续、分布广、无污染等优点,风力发电机是将风能转化为电能的装置。风力发电机叶片的造价占整个风力发电机的1/3[1],叶片在旋转时外界激振频率接近或等于叶片的固有频率,会产生共振。共振对风力发电机叶片的危害非常大,因此对风力发电机的设计人员而言，需要尽可能改善叶片的固有频率,使风力发电机减小或者避免共振的危害。

对风力发电机叶片固有频率进行研究,通常有计算模态与试验模态两个方面。在计算模态方面,高伟等[2]对风力发电机叶片加装L形小翼和T形小翼,并分别进行了模态分析;张志勇[3]设计了不同的叶片截面形式,应用有限元方法进行了模态测试;邢帅恒等[4]对复合材料铺层角度与模态参数的关联机制进行了研究;Gangele等[5]对1.5 MW风力发电机叶片进行了模态测试;Dai Feili等[6]对风力发电机叶片的襟翼进行了模态分析。在试验模态方面,马剑龙等[7]研究了风力发电机叶片加装S形小翼对叶片模态参数的影响;张建伟等[8]对叶片进行V形叶尖改型,研究叶片改型对固有频率的影响;汪建文等[9]分析了叶片数量变化对模态参数的影响;韩巧丽等[10]对新型木芯叶片进行破坏载荷及模态特性研究;Griffith等[11]应用模态试验法，测试不同翼型的弯扭耦合点。通过文献分析可知，目前国内外对于风力发电机叶片固有频率的改善，大部分集中在叶尖加装小翼或是叶片自身结构方面,对于叶尖改型的研究则较少。

为了确定一种改善风力发电机叶片固有频率的方法,笔者提出一种风力发电机叶片双叉式叶尖结构方案,并通过模态试验的方法,分析双叉式叶尖结构对风力发电机叶片固有频率的影响。

2 模态试验方案

2.1 试验对象

试验对象为300 W小型风力发电机叶片,装机叶片数为三片,被测叶片如图1所示。规定叶片轴向方向为X轴方向,宽度方向为Z轴方向,厚度方向为Y轴方向。额定风速为8 m/s,额定转速为600 r/min。双叉式叶尖改型方案来源于民用客机采用的双叉式机翼,这一机翼设计可以减小飞行过程中的阻力,具有减振、降噪、省油等优点。双叉式叶尖结构尺寸中，叶尖夹角θ为60°,叶尖长度a为4.7 cm，叶尖宽度h为4.5 cm。双叉式叶尖结构尺寸如图2所示。

▲图1 被测叶片

2.2 试验原理

模态试验的原理是瞬态激振法,采用手持式力锤对叶片施加激励。叶片受到激励后被迫振动,此时粘贴在叶片表面的加速度传感器采集原始振动信号。由计算机应用BK Connect软件识别并处理所采集的原始振动信号,得到叶片振动时的频响函数。通过对频响函数进行后处理及计算，便可以得到叶片的固有频率等参数。

▲图2 双叉式叶尖结构尺寸

2.3 测点布置

试验采取多点激励、多点响应的测点布置方案,可获得所有模态振型。在叶片表面均匀布置18个Z向测点，用于测试风力发电机叶片的挥舞及扭转振型。如图3所示,1～18为测点,设置传感器频率采集范围为0～400 Hz；19～22为力锤激励点,需要人力进行Y向激励,每次试验激励敲击次数为五次。

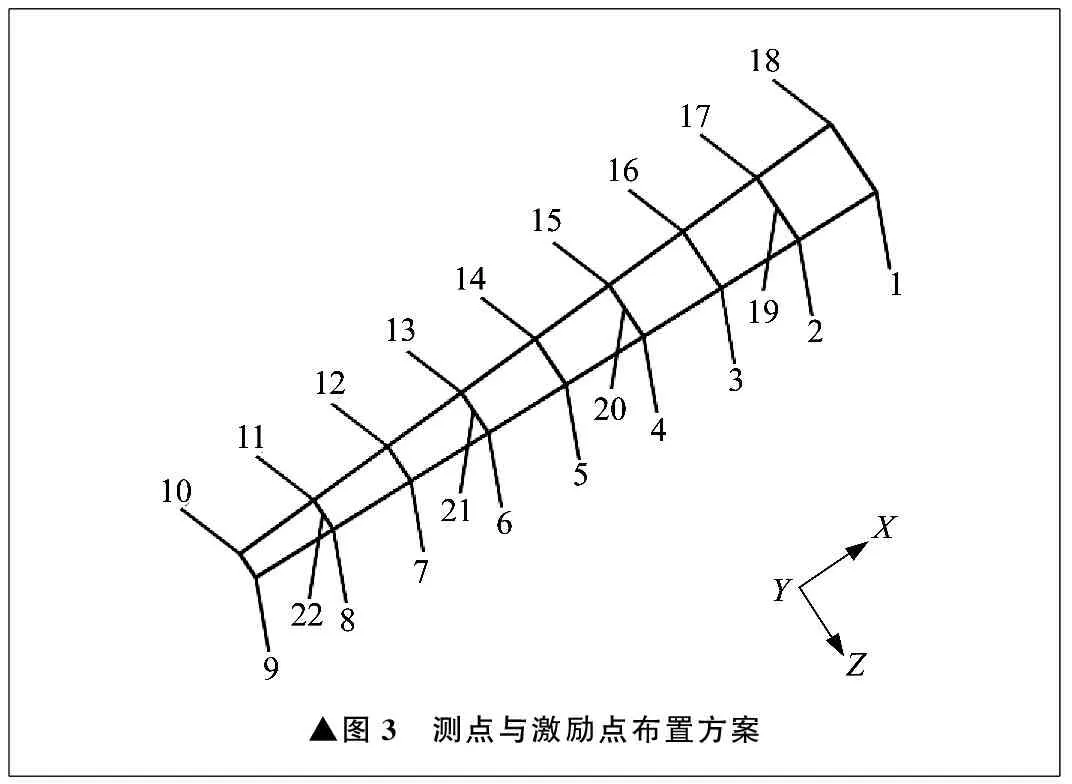
▲图3 测点与激励点布置方案

3 风洞动频试验方案

3.1 试验对象与试验原理

试验对象与模态试验一致,试验原理为频谱分析法。调整风洞风速为额定风速8 m/s,在风力发电机风轮受气动载荷而旋转时,同时通过三向加速度传感器记录动频振动信号。对采集到的振动频谱进行快速傅里叶变换,再通过频谱分析法提取动频频率数据。

3.2 测点布置

风洞动频试验共布置两个三向加速度传感器,分别位于风力发电机机头靠近风轮的前端与中端。基于所采集到的振动频谱，结合模态试验采集到的静态振动频谱,通过频谱分析法可以间接识别出风轮的动频频率[12]。

4 试验结果

4.1 叶片固有频率

叶片前六阶固有频率见表1。由表1可知,双叉式叶尖结构叶片的前四阶固有频率较原结构叶片有降低的趋势,五阶、六阶固有频率有升高的趋势。双叉式叶尖结构叶片五阶固有频率较原结构叶片提高了16.38%,六阶固有频率提高了8.87%。通过分析可知，双叉式叶尖结构可以改善叶片的固有频率。

表1 叶片前六阶固有频率 Hz

4.2 叶片振型

原结构叶片前六阶振型如图4所示。由图4可知，一阶振型为叶尖、叶中、叶根小幅度扭转；二阶振型为叶尖小幅度扭转,叶中、叶根大幅度扭转,且前缘出现大幅度扭转；三阶振型为叶尖、叶中、叶根大幅度扭转,且前缘出现大幅度扭转；四阶振型与三阶振型类似；五阶振型为叶尖小幅度扭转,叶中、叶根大幅度扭转,且前缘出现大幅度扭转；六阶振型与五阶振型类似。由振型分析可知,原结构叶片振型较有规律。

▲图4 原结构叶片前六阶振型

双叉式叶尖结构叶片前六阶振型如图5所示。由图5可知，一阶振型为叶尖、叶中大幅度扭转,叶根小幅度扭转;二阶振型与一阶振型类似；三阶振型为叶尖、叶中大幅度挥舞,叶根小幅度扭转；四阶振型与三阶振型类似；五阶振型为叶尖大幅度挥舞,叶中、叶根大幅度扭转；六阶振型为叶尖、叶中、叶根大幅度扭转。通过与原结构叶片振型对比分析可知,一阶振型双叉式叶尖结构叶片在叶尖出现大幅度扭转,比原结构差；三阶、四阶、五阶振型双叉式叶尖结构叶片在叶尖与叶中出现挥舞,而原结构叶片为扭转振型,且叶片前缘大幅度扭转振型消失,证明双叉式叶尖结构改善了原结构叶片的静态振动特性。

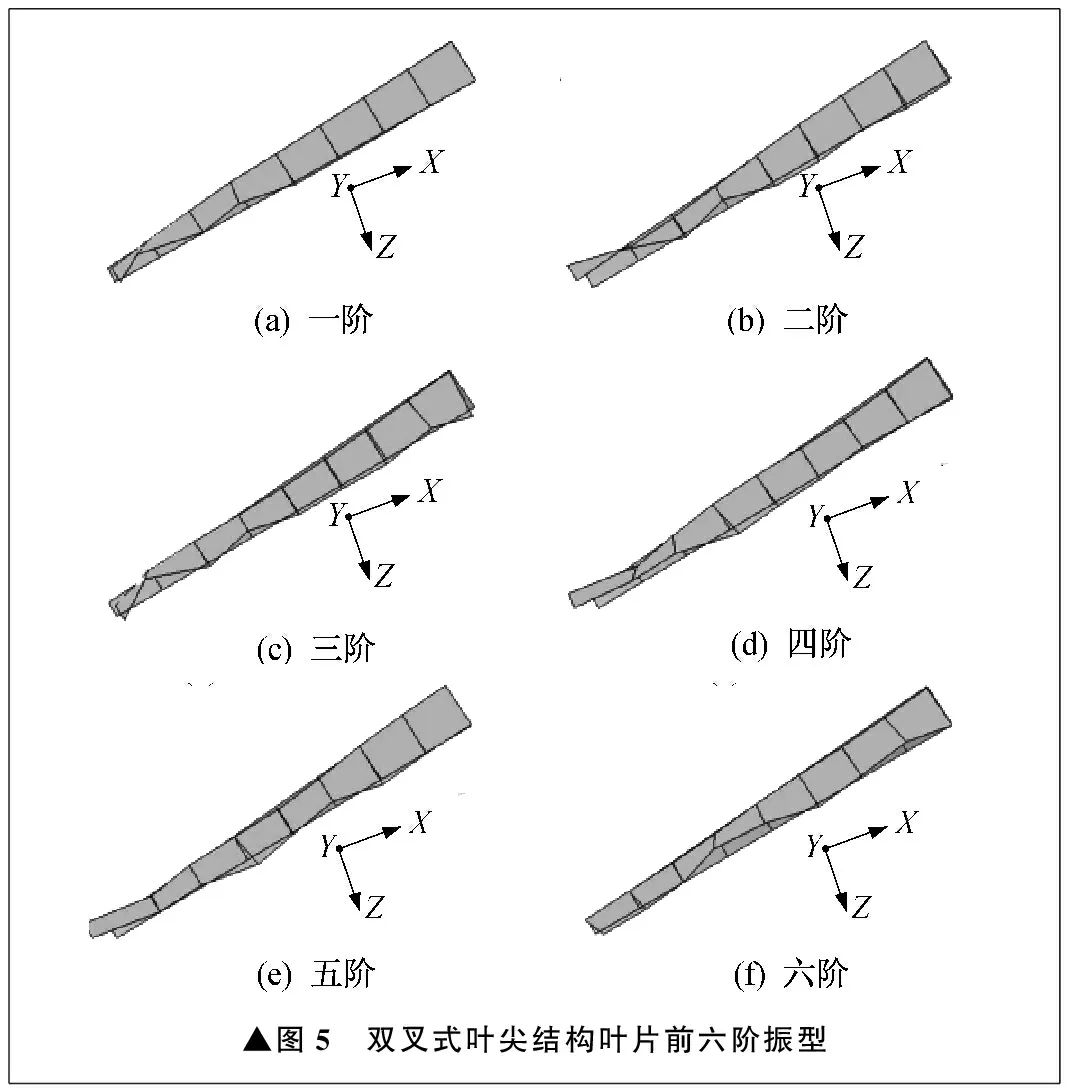
▲图5 双叉式叶尖结构叶片前六阶振型

由图4与图5分析可知,双叉式叶尖结构叶片可将原结构叶片的一部分扭转振型改变为挥舞振型,明显改善了原结构叶片前缘出现的大幅度扭转振型。因此，双叉式叶尖结构可以改善叶片的静态振动特性。

4.3 叶片动频

风轮的动频数据以坎贝尔图的形式来进行分析。由坎贝尔图原点引出的多条射线为激振频率射线，旋转基频为P。风轮一阶坎贝尔图如图6所示。对于三叶片风轮的风力发电机而言,可以认为基频的三倍频，即3P是主激振源频率。将±10%主激振源频率范围设置为共振区,在图6中以虚线为界表示。风轮动频曲线与共振区的两个交点所对应动频频率之间的差值为风轮动频曲线穿过共振区的频宽,此频宽越窄,说明风轮处于共振区的时间越短,能更快地脱离共振区。风轮动频曲线与主激振源频率3P的交点所对应的转速即为共振点的转速,此转速越接近额定转速,说明风轮在正常工况下工作时产生共振概率的越大[13]。

由图6可知，双叉式叶尖结构叶片的整体动频曲线位于原结构叶片下方,因此双叉式叶尖结构叶片可调整风轮动频曲线的走势。原结构叶片的动频曲线与共振区交点的风轮动频率为40.28 Hz、36.07 Hz,两者之差4.21 Hz即为原结构叶片的共振区频宽，与主激振源频率3P射线的交点即为共振点所对应的风轮转速403.53 r/min。双叉式叶尖结构叶片的动频曲线与共振区交点的风轮动频率为32.76 Hz、31.54 Hz,两者之差1.22 Hz即为双叉式叶尖结构叶片的共振区频宽,与主激振源频率3P射线的交点即为共振点所对应的风轮转速343.39 r/min。

▲图6 风轮一阶坎贝尔图

通过以上数据比较可知，双叉式叶尖结构叶片的共振区频宽为1.22 Hz，明显小于原结构叶片共振区频宽4.21 Hz,且双叉式叶尖结构叶片共振点对应的风轮转速343.39 r/min较原结构叶片共振点对应的风轮转速403.53 r/min更远离额定转速600 r/min,说明双叉式叶尖结构叶片可使风轮进入共振区的时间变短,使风轮能够更快脱离共振区。因此，双叉式叶尖结构可以改善风力发电机风轮的动频特性。

5 结束语

笔者研究双叉式叶尖结构能否改善叶片的固有频率、振型，以及风轮动频频率,进行了风力发电机叶片模态试验与风洞试验,分析数据得出如下结论:

(1) 双叉式叶尖结构叶片相较原结构叶片，前四阶固有频率降低,五阶、六阶固有频率升高，由此可知双叉式叶尖结构可以改善叶片的固有频率；

(2) 双叉式叶尖结构可将原结构叶片的一部分扭转振型改变为挥舞振型,且明显改善了原结构叶片前缘出现的大幅度扭转振型，因此，双叉式叶尖结构可以改善叶片的静态振动特性；

(3) 双叉式叶尖结构可以调整风力发电机风轮动频曲线的走势,使风轮进入共振区的时间变短,从而可以快速脱离共振区，所以双叉式叶尖结构可以改善叶片的动频振动特性。

综合研究结果可知,双叉式叶尖结构可以改善叶片的固有频率、振型，以及风轮动频频率,为风力发电机叶片的减振研究提供了基础。