机床伺服进给系统在机可靠性加速试验与评估方法*

□ 周大朝 □ 辛庆伟 □ 邢诺贝 □ 刘福军 □ 胡德金 □ 许黎明

上海交通大学 机械与动力工程学院 上海 200240

1 研究背景

伺服进给系统作为数控机床实现精确运动的核心部件之一,其性能对机床的加工精度和生产效率有决定性影响,尤其在大批量汽车零部件生产行业中,一旦出现故障，将对生产节拍造成严重影响。因此，数控机床伺服进给系统的可靠性研究尤为重要。

机床功能部件的可靠性评估是保障机床可靠性水平的关键环节。由于机床伺服进给系统的可靠性水平较高,无法在短期内收集到有效的故障数据,传统的功能部件可靠性评估需要专门的试验台架和很长的试验时间[1]。朱倩等[2-4]针对滚动直线导轨副进行了可靠性试验相关研究,建立了滚动直线导轨副的试验平台，并在此基础上对滚动直线导轨的可靠性评估方法展开了深入研究。高山龙等[5]自主设计了滚珠丝杠副精度保持性试验台,填补了国内在此领域内的空白。邓超等[6]利用反向传播神经网络对进给系统定位精度进行预测,对定位精度与失效阈值进行了建模,并对进给系统剩余寿命进行了预估。王民等[7]开展了滚珠丝杠副加速退化仿真试验研究,实现了滚珠丝杠副寿命的快速预测。姚玲峰等[8]确定了滚珠丝杠副的寿命模型,并设计了相应的试验方案。

由以上介绍可见,国内机床伺服进给系统的可靠性评估技术相关研究主要基于独立的功能部件试验平台。可靠性加速试验是目前高可靠性产品采用的一种可靠性试验方法,但针对伺服进给系统的在机可靠性加速试验研究还较少。笔者基于机床伺服进给系统的性能退化数据，对机床伺服进给系统性能退化趋势进行建模,快速评估机床伺服进给系统的可靠性,预测其性能失效时间。这一方法克服了传统可靠性试验周期长、失效数据少或不出现的困难,节约了试验成本,缩短了试验时间。

2 机床伺服进给系统性能退化量指标

机床伺服进给系统是可靠性高、使用寿命长的部件,性能退化失效是导致设备失效的主要原因,因此，机床伺服进给系统的可靠性可以在性能退化过程中得到反映。

机床伺服进给系统性能退化量指标的选取需满足以下条件:① 能够在试验系统中直接测量;② 能够作为设备可靠性的评判依据;③ 在试验时间内具备较明显的性能退化趋势。

机床伺服进给系统性能失效的主要表现是精度失效,其失效过程，即精度退化主要表征为加工精度退化、位置精度退化、几何精度退化。对于加工精度，需要测量工件的精度,过于复杂，成本高,且加工精度是机床精度的综合反映,因此不适合作为退化指标。影响几何精度退化的最主要原因是机床丝杠、导轨及机床床身刚度,在无外界因素干扰的情况下,变化很小。位置精度是机床伺服进给系统可靠性研究中最常用的性能指标,符合性能退化量指标选取需要满足的三个条件,因此将位置精度作为机床伺服进给系统可靠性评估中的性能退化量指标。

3 机床伺服进给系统在机可靠性加速试验

根据累积损伤理论,产品短时间高应力与长时间低应力作用下的损伤程度是一致的[9],即当产品退化失效机理一致时,产品可靠性指标取决于应力水平,由不同应力水平获取的可靠性指标估计值不同,需要将其等效为正常应力水平下的可靠性指标估计值。应力水平与可靠性指标的对应关系被称为加速模型,目前广泛使用的模型有Arrhenius模型、逆幂律模型等。考虑到机床伺服进给系统为机电一体化产品,采用逆幂律模型对加速模型进行建模。

根据可靠性加速试验原理和加速模型对进给系统在机可靠性加速试验进行设计,设计内容包括试验流程、试验加载方式、试验剖面、试验数据采集方案。

3.1 试验流程

根据试验条件对以下试验参数进行设定:① 试验所需样本数量;② 试验加载应力水平数量;③ 试验时每一个应力水平下的试验样本数量;④ 数据测量点的测量时间间隔;⑤ 试验的截止时间。

针对汽车零部件批量生产用加工中心伺服进给系统,以X轴加载为例，制订以下试验流程：① 加载试验开始,选取加载应力水平，初始值为SL1,在该应力水平下对X轴进给方向进行加载;② 加载持续1.4 h,同时对驱动电流信号进行采集;③ 1.4 h后对X轴进行位置精度测量,返回第②步,直至12次测量结束;④ 恢复伺服进给轴位置精度,改变加载应力水平至SL2,返回第①步,直至应力水平SL5加载结束;⑤X轴加载试验结束。

应力水平的选取非常关键,若取值过高,则有可能破坏机床,对机床造成损伤;若取值过低,则性能退化程度不明显,无法获取有效数据。参考相关文献[10],试验中将应力水平选取为试验轴方向最大切削抗力的60%～80%,见表1。

表1 应力水平选取

3.2 试验加载方式

在机可靠性加速试验中,模拟主轴切削实现对进给轴的加载。为了消除其它功能部件对试验进给轴的影响,采用对主轴单方向力加载的方式。主轴力加载主要有三种方式,分别为伺服电机加载、液压缸加载和气缸加载。试验中采用气动加载作为主轴进给切削抗力加载方式,X轴方向上气缸加载试验如图1所示。

▲图1 X轴方向气缸加载试验

3.3 试验剖面

试验剖面指针对某个伺服进给轴进行加速加载时的机床试验动作流程。以X轴加速加载试验为例,其试验剖面流程如下:① 主轴移动至换刀位,换上特定刀具;② 将主轴与工作台移动至预设工作原点;③ 主轴正向旋转,提高转速至500 r/min;④ 主轴以300 mm/min的速度沿X轴正向匀速进给60 mm,随后负向快移60 mm至工作原点,重复运动持续1.4 h；⑤ 结束流程。

3.4 试验数据采集

试验数据采集主要分为位置精度测量和伺服电机电流测量。位置精度测量主要采集机床伺服进给系统性能退化量的变化情况,包含定位精度与重复定位精度。伺服电机电流测量用于定量评估加载应力水平。

位置精度的测量设备为Renishaw80XL激光干涉仪,伺服电机的电流数据则由采集软件从数控系统中实时提取。

4 机床伺服进给系统在机可靠性评估方法

根据加速试验要求,施加在被试部件上的载荷要高于正常应力水平。对此，笔者提出一种加速应力水平下基于性能退化的功能部件在机可靠性评估方法。

(1) 在可靠性试验阶段对每个样本进行m个不同应力水平的加载,同时记录给定样本在n个时刻时的性能退化数据,记为t11、t12、…、t1n，t21、t22、…、t2n，…，tm1、tm2、…、tmn。依据性能退化数据表现出的规律,选择适当的退化模型。对于进给系统,退化失效过程利用Wiener过程进行拟合。

(2) 根据试验获得的性能退化数据,利用点估计等方法，估计各个样本所匹配的性能退化模型的未知参数。

(3) 根据机床伺服进给系统的设计指标要求,设定样本达到性能失效的阈值Df。通过第(2)步中求得的退化轨迹模型,外推出各样本在给定应力水平情况下达到失效阈值的时间,即伪失效寿命时间,记为T11、T12、…、T1m,T21、T22、…、T2m，…，Tl1、Tl2、…、Tlm。其中，l为样本编号。

(4) 根据不同机床伺服进给系统的种类及不同的应力水平强化类型,选取不同的加速模型对各个样本在正常情况下的失效寿命时间进行外推,依次记作Γ1、Γ2、…、Γl。

(5) 对伪失效寿命时间数据进行分布假设检验。根据产品类型与失效机理,选择韦布尔分布作为分布模型。

(6) 将第(4)步中计算得出的伪失效寿命时间数据视作真实失效数据,根据所选定的分布模型,对机床伺服进给系统可靠性进行评估。

5 应用案例

根据在机可靠性加速试验设计方法,对某型四轴卧式加工中心的伺服进给系统进行在机可靠性试验,试验中定时测量各个进给轴的重复定位精度,结果如图2所示。

▲图2 各轴不同应力水平重复定位精度变化曲线

利用Wiener过程对机床伺服进给系统的性能退化轨迹进行建模。Wiener函数G(t)用于表征产品在t时刻的性能退化量:

G(t)=μt+σB(t)

(1)

式中：t为试验时间；B(t)为[0,+]上的正态分布N(0,t);μ为漂移因数，μ>0;σ为扩散因数，σ>0。

当G(t)≥w时,机床伺服进给系统因性能退化而失效。机床伺服进给系统失效时间Td为：

Td=inf{t|G(t)=w}

(2)

失效时间为逆高斯分布,其分布函数Fd(t)为:

(3)

概率密度函数fd(t)为:

(4)

可靠度Rd为:

(5)

以X轴在SL4应力水平下的性能退化数据为例,利用极大似然估计可以得到Wiener过程可靠度模型为：

(6)

相应的可靠度曲线如图3所示。

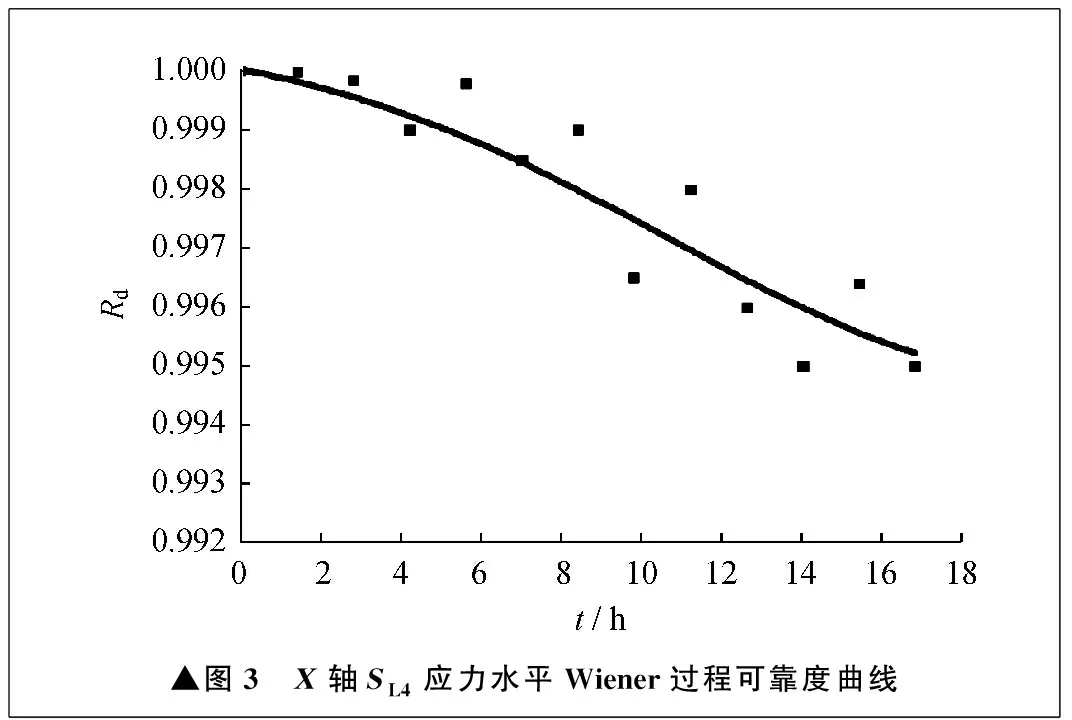
▲图3 X轴SL4应力水平Wiener过程可靠度曲线

一般而言，当机械设备可靠度大于90%时，可以认定机械设备不发生失效,可将可靠度90%对应的时间作为伪失效寿命时间[11]。将可靠度模型外推,可计算出各轴在不同应力水平下的伪失效寿命时间,结果见表2。

机床伺服进给系统轴的动力来源为各轴伺服电机,所以机床伺服进给系统轴所受到的载荷可通过电机的负载电流或功率来体现。试验中各个加载轴的应力水平通过相应的伺服轴电流有效值与正常加工电流有效值相比较来量化评估,确定逆幂律模型的参数。

通过最小二乘拟合,得出X轴的加速模型曲线函数为:

lnξ=9.096 50-1.045 59lnv

(7)

Y轴的加速模型曲线函数为:

lnξ=9.069 90-1.164 18lnv

(8)

Z轴的加速模型曲线函数为:

lnξ=9.077 79-1.003 97lnv

(9)

式中：v为应力水平；ξ为伪失效寿命时间。

算得X、Y、Z轴正常工况下的伪失效寿命时间依次为8 924.03 h、8 889.75 h、8 758.61 h。

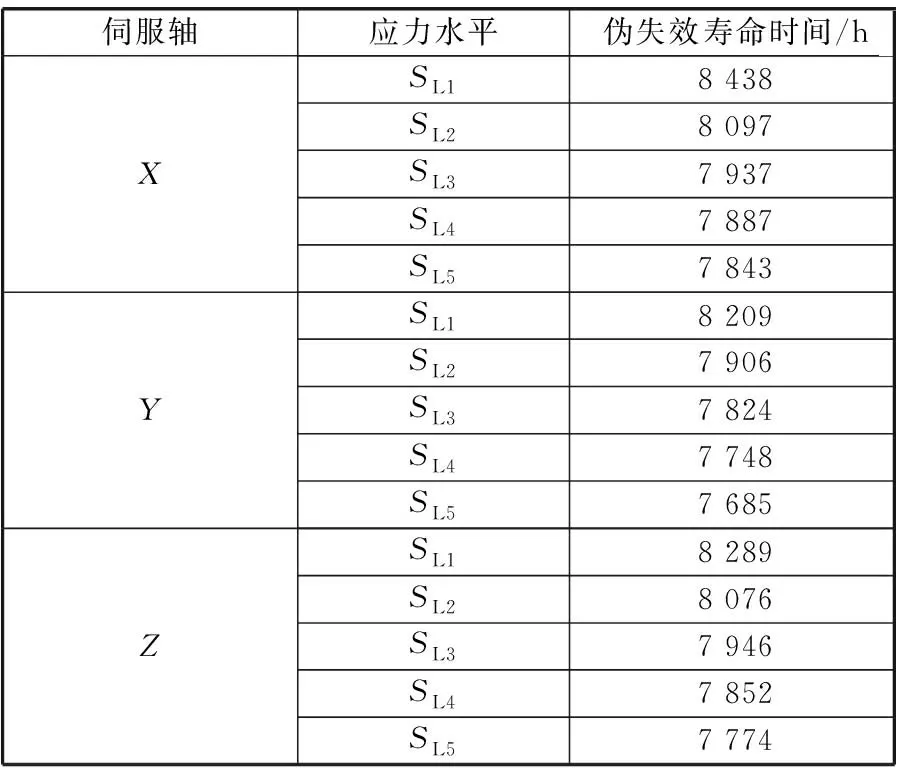
表2 各轴不同应力水平伪失效寿命时间

通过双参数韦布尔分布模型对机床伺服进给系统可靠性水平进行评估,得出形状参数β为3.748,位置参数θ为9 762.0,最后得到机床伺服进给系统的可靠性指标故障间隔时间MTBF为:

MTBF=θΓ(1+1/β)=8 816 h

式中：Γ(1+1/β)为伽马函数。

依据应用于某生产线上的同类型进给系统精度失效统计结果,该类型机床伺服进给系统的故障间隔时间一般长于9 000 h,由此可见,可靠性估计结果基本能反映生产实际,存在估计量偏差的原因有两方面。第一，样本数量较少。本试验主要对加工中心三根轴的性能退化量进行性能可靠性评估。第二，试验时长较短。性能退化量的变化和试验时间的相关性强,缩短时间在提高效率的同时,也会影响可靠性建模的精度。因此,若试验条件允许,可以适当增加试验时间，以提高评估精度。

6 结束语

笔者基于机床伺服进给系统性能退化原理设计了机床伺服进给系统在机可靠性试验,并提出了一种加速应力水平下基于性能退化数据的可靠性评估方法,完成了在机进给功能部件的快速可靠性试验,同时通过数学建模对机床伺服进给系统的可靠性指标进行了评估。

所得结果较好地反映了机床伺服进给系统的性能可靠性水平,有助于节约试验时间和成本,为进一步提高机床伺服进给系统的可靠性提供数据支持。