玻璃自重对索网结构幕墙自振特性的影响
2020-06-09陈子立
陈子立
(四川电力设计咨询有限责任公司 四川成都 610041)
0 引言
目前,现有的对单层平面索网玻璃幕墙结构的研究工作以及频域分析设计方法多是在认为竖索预应力非常大而忽略玻璃自重对其拉力沿索向产生的影响的情况下得到的结论,而在实际工程中这种影响是真实明显存在的,使得竖索的上部预应力显著加大而下部预应力显著减小,这将对单层索网玻璃幕墙的自振特性尤其是振型产生较大影响,进而对据此进行的风振频域分析的结果产生一定的影响。已经发现采用通常的频域设计方法忽略拉索和玻璃重量对结构的影响而设计出来的结构,在挠度和索预拉力方面的实测值与理论计算值之间还是有比较大的差别,所以从合理与安全性角度考虑,进一步更准确的分析出结构的实际状态是有必要的。
1 索网幕墙的自振特性解析
在对索网幕墙进行自振特性分析之前,对索需要作出一些基本假设:索为理想的柔性,不考虑它的抗弯刚度和抗扭刚度;虎克定律适用于索的应力应变分析;索的自振是在静风平衡位置附近作微幅的自由振动;自由振动时不考虑阻尼影响;仅考虑顺风向荷载的位移,忽略其他方向的位移。
1.1 忽略自重影响
在实际工程的常用高宽比范围内,当不考虑玻璃自重对竖索拉力的影响时,结合竖索、横索及索网的振型特点,可以假设索网前六阶振型函数为:
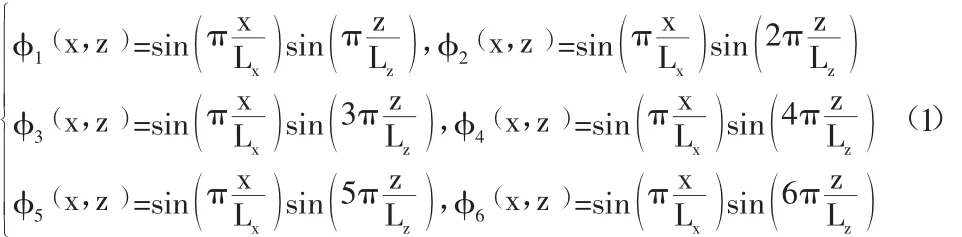
以动力荷载作用下结构振动的第一阶模态为例来说明,其他阶的自振特性分析方法与此类似。
取结构中心处最大位移为w(t),则结构上任意点的位移可表示成:

把相关计算式代入到振动微分方程中并且对索网进行积分,得到经过简化的整体结构的无阻尼自由振动微分方程如下:
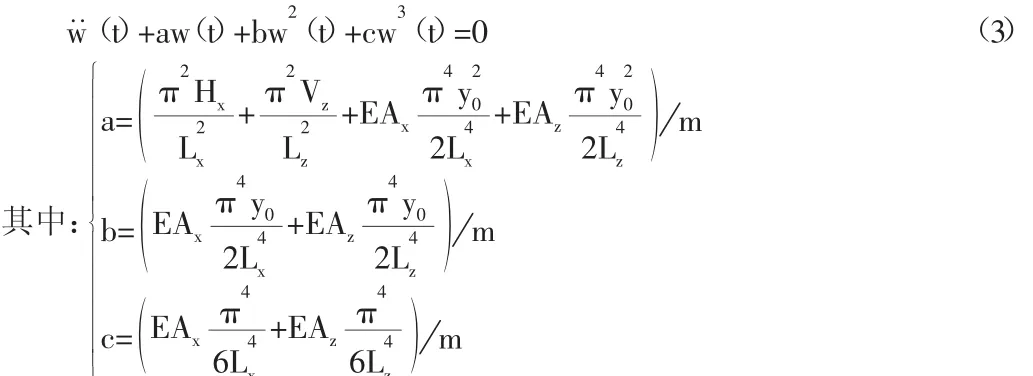
y0为平均风作用下的跨中位移。
可以看出,刚度的线性项和非线性项分别是:

求解结构的振动频率时可考虑对其等效线性化处理。考虑到非线性方程中同时含有立方和平方非线性项,可以假设位移包含一次、二次谐波及常数的解为:

将其代入到结构无阻尼自由振动微分方程中计算可以得到:

由于A1与结构从初始位置开始振动的位移w=Acosωt中的A相差非常小,故可认为A1=A。由此可见,结构的非线性程度是和振幅A即跨度L密切相关的。由于频域分析是认为其在处于平均风压位置作微幅振动,结构的非线性大部分已经完成的情况下,对其进行的线性化分析,故实际上其频率计算可以只考虑线性项来计算。
1.2 考虑自重影响
在实际工程的常用高宽比范围内,当考虑玻璃自重对竖索拉力的影响时,结合竖索、横索及索网的振型特点,考虑如下几种振型:
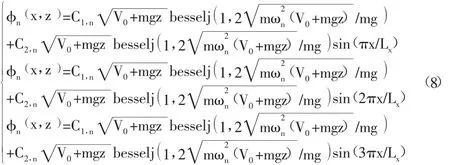
式中:n=1,2,3,4,5,6。
上面假设的三种振型函数主要差别体现在横索的振型形式的不同上,因为横索并不考虑自重的影响,只存在一个均布荷载,可以假设其振型为正弦函数形式,并且根据已考虑自重影响后的竖索结构的振型特点,则可以假设出如上述三种形式的索网幕墙结构振型函数。然后把上述三种索网振型分别带入到自由振动微分方程中,根据结构的自振频率从低到高的原则,可解出索网幕墙结构的前六阶频率,这六个频率对应的振型即为索网幕墙结构的前六阶振型函数。
以结构振动的第一阶模态为例来说明,其他阶的自振特性分析方法与此类似。
取结构中心处最大位移为w(t),则结构上任意点的位移可表示成:
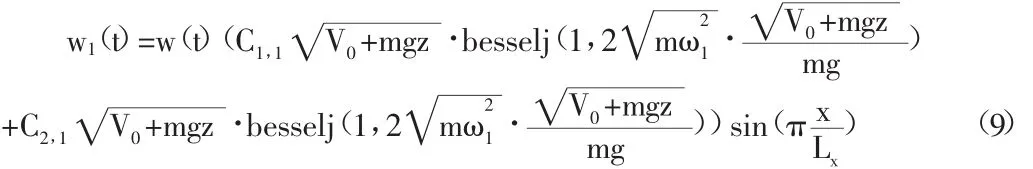
式中:C1,1=18;C2,1=-1;ω1=1.95 为单根竖索竖直状态振动的第一阶频率,m为索单位长度质量。
把相关计算式代入到振动微分方程中并且对索网进行积分,此时考虑了自重影响的索网幕墙结构的刚度也如前面分析的不考虑自重影响时索网的结构的刚度是分为线性部分和非线性部分的,但是由于方程及解的解析表达式都非常繁杂且某些积分式无法积出解析解,所以对于频率的计算无法像不考虑自重影响时那样得到解析频率的解析表达式,而只能采用数值积分的方法来得到数值解,故中间一些计算结果形式不在文中列出。与前面同样地,实际上,由于对单层平面索网玻璃幕墙结构进行的频域分析是认为其在处于平均风作用位置作微幅振动,结构的非线性大部分已经完成的情况下,对其进行的线性化分析,故实际上其频率计算可以只考虑线性项来计算。
1.3 索网幕墙的算例验证
以某大厦单层平面索网幕墙为基础,竖向为60m,水平向为30m的单层平面索网,竖索初始预拉力为75kN,横索初始预拉力为250kN,索密度为7850kg/m3,直径为0.02m,弹性模量为1.04×1011Pa,每 1m2网格的节点挂着1m2的玻璃板,单位面积玻璃自重为500N/m2,10m高度处风速为22m/s,取2/3高度处的平均风荷载均布作用。以左下角为坐标原点,向上和向右为正方向,对结构的自振特性进行计算,比较是否考虑玻璃自重对结构的自振特性的影响。
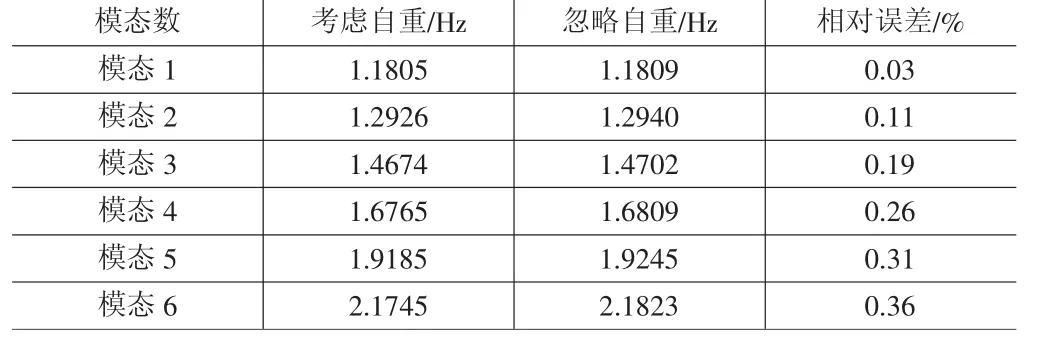
表1 索网幕墙考虑自重与否的自振频率
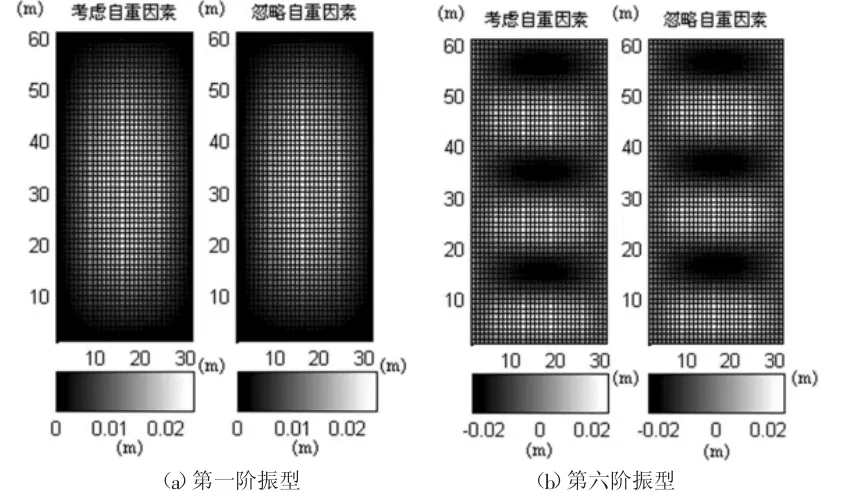
图1 索网幕墙第一阶和第六阶考虑自重与否的振型
以对结构的风振响应起主要控制作用的第一阶模态为例来说明随着自重的变化,结构的自振特性的变化规律。
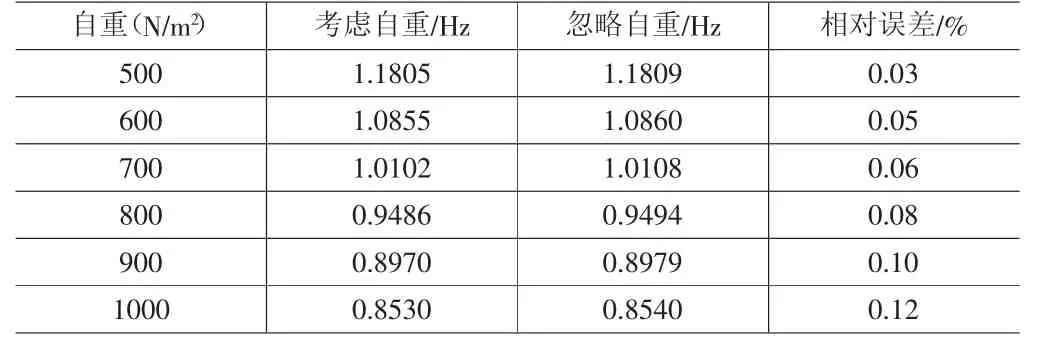
表2 索网幕墙考虑自重与否第一阶频率的变化

图2 索网幕墙自重500N/m2和1000N/m2考虑与否第一阶振型的变化
2 结论
本文分析了在考虑玻璃自重对竖索拉力影响与否时的索网幕墙结构自振频率及其振型,发现忽略自重影响和考虑自重影响时结构频率差别不大但振型差别较大且随着自重的增大,这种差别愈发显著。
索网结构玻璃幕墙考虑了玻璃自重对竖索张力的改变会使得结构的自振频率及其振型结果发生变化,但是就频率而言这种变化非常比较小,变化主要体现在振型产生了整体下移的改变上。
随着自重的增加,结构振型的下移有加剧的趋势,频率的差异也有加剧的趋势,若忽略这种影响,结构的振型将始终以跨中为对称点,这也使得若继续假设不考虑玻璃自重对竖索张力的改变来分析结构的自振频率及振型,将产生越来越大的误差。
