基于ILS-PSO 算法的移动云计算DAG 图的任务调度研究与应用*

董 韵 张 毅 孙 晋

（南京理工大学计算机科学与工程学院 南京 210094）

1 引言

移动云计算（Mobile Cloud Computing，MCC）的概念基于云计算提出，是云计算和移动网络融合的产物，作为一种全新的交付模式，将任务分布在由大量移动设备构成的网络上。移动云计算的主要目标是利用云端的计算、存储等资源优势，突破移动设备的资源限制，通过无线网络以按需、可扩展的模式从云端获得所需的基础设施、平台和软件等［1～2］。

随着4G 网络成熟并广泛应用，移动通信开始朝向5G 的发展阶段大步迈进，促进了移动网络的飞速发展和移动应用的极大丰富，移动设备已经渗透到人们生活和工作的方方面面［3］。但是移动设备与传统的PC设备相比较，具有计算速度慢、存储容量少、安全性差等缺点，同时还存在电池容量的限制，移动设备的硬件缺陷成为了移动应用智能化发展的瓶颈［4］。

通过将云计算引入移动网络，将移动应用迁移到移动设备网络中执行，来弥补单个移动设备计算速度慢、存储容量少的缺点，减少移动设备所消耗的电量，保证整个网络 QoS［5～6］，缩短移动应用的执行时间。

移动云计算的任务调度是一种组合优化问题，已被证明是NP 完全问题，无法在多项式时间内求解［7～8］。目前对于移动云计算的任务调度的研究成果［9～11］，大多是针对同构设备构成的网络提出的，对于异构设备网络下的任务调度研究有待进一步深入。任务调度问题根据任务类型的不同分为独立任务调度和关联任务调度，关联任务调度更符合于实际应用的运行情况。

电池容量是移动设备本身具有的局限性，是移动云计算的一种内在的约束性，本文针对移动云计算异构设备网络的任务调度问题，移动设备的电池容量能够满足所执行任务消耗电量的前提下，提出了一种应用迭代局部搜索策略（ILS）的粒子群优化算法（PSO），求解最优调度方案的方法，并在Cloud-Sim 云计算仿真平台上进行实验以验证算法的有效性。

2 任务调度数学模型

使用DAG 图对移动云计算环境下的应用进行建模，记作DAG={T，E，W}，节点集T={t1，t2，…，tn}表示任务的集合；E是有向边的集合，从ti指向tj的有向边记作eij，如果eij∈E，表示任务ti和tj之间存在依赖关系，tj要在ti完成之后才能执行；W是有向边的权值集合，∀eij∈E存在|eij|∈W，表示ti和tj之间的通信量。

网络中的移动设备集记为D={d1，d2，…，dm} ，移动设备的计算性能为MIPS={mips1，mips2，…，

由于移动设备资源受限，无法满足如视频处理、实时大数据分析等复杂应用的要求，阻碍了此类应用在移动云计算环境下的有效运行。对于可用有向无环图（Directed Acyclic Graph，DAG）表示的应用，在移动云环境中将应用划分成多个不相交的集合分配至移动设备上执行，使得每个移动设备的可用资源能满足所分配部分的资源要求。如何有效划分应用是移动云计算领域的重要研究问题，称为应用划分问题，也称为任务调度［12］。

2.1 数学模型

mipsm}表示，电池容量为BC={bc1，bc2，…，bcm} 。由于移动云网络是异构的，移动设备的处理性能各不相同，任务在各个设备执行所需时间也各不相同 。使 用 向 量ci={ci1，…，cin}={s(ti)mips1，…，s(ti)mipsn}表示任务ti在各移动设备上的执行时间，s(ti)是任务ti的长度。

为了便于确定任务的开始执行时间和构建任务间的依赖关系，定义DAG 图上任务的高度height［13］：

其中ti∈T，pred(ti)是任务ti的前驱任务集合。任务高度函数可以表示任务之间执行关系，如果从ti到tj之间存在一条路径，则有ti在tj之前执行并且height(ti)＜height(tj)；如果两个任务之间不存在路径，那么它们之间的执行顺序可以是任意的，但是要保证处理器之间的优先关系。任务高度height的缺点是最优的任务调度方案可能无法满足式（1），为减少这种可能性的发生，定义任务高度height［'14］：

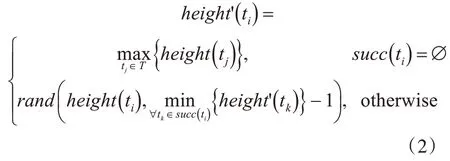
其中，succ(ti)是ti的后继任务的集合，rand(a，b)是在区间[a，b] 上的随机整数。没有前驱节点的任务称为入口任务，对应着height'最小的节点；没有后继节点的任务称为出口任务，对应着height'最大的节点。为方便研究，规定DAG 任务图只有一个入口任务和一个出口任务。

2.2 优化目标

为了方便研究，除了上述数学模型，做出如下假设：1）任务是非抢占的，相同任务不能同时在两个及以上移动设备上运行；2）每个虚拟机同一时刻只能处理一个任务；3）具有依赖关系的任务，前驱任务执行完成，后继任务获得依赖数据后才能执行；4）具有依赖关系的任务分配在不同移动设备执行时才考虑网络通信开销；5）移动设备网络是全互连结构，每个移动设备到任意设备都存在路径。

移动云计算任务调度的目标函数定义如下：移动云计算的DAG 任务图中的任务分配给特定的移动设备，使得应用的完成时间最小，形式化描述如下：

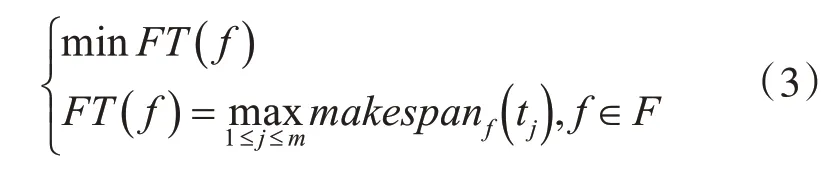
其中F 是可行调度方案集，f 是一种可行的调度方案，makespan是移动设备上最后一个任务的完成时间，FT 是在调度方案f 下应用的最早完成时间［15］。

分配到设备dj的任务集T，应满足在移动设备上执行任务所消耗的电量不应超过设备的电池容量，则目标函数应该满足如下条件：

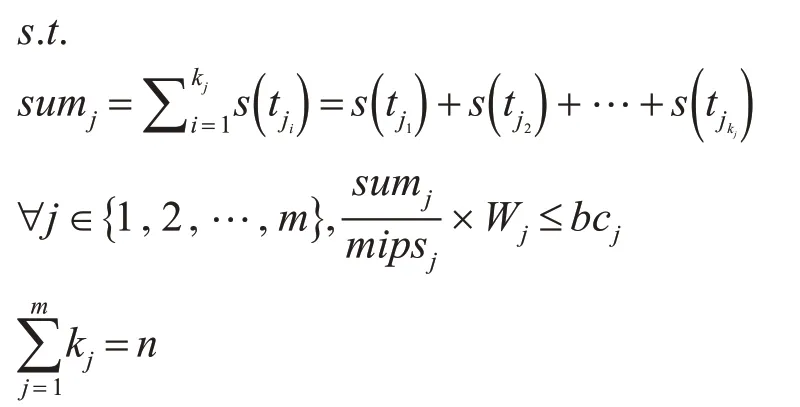
其中Wj是移动设备dj的功率，sumj是在dj上执行的任务的长度之和，应满足分配给各个移动设备的任务个数之和等于任务总数n。

3 粒子群优化算法

粒子群优化（Particle Swarm Optimizer，PSO）算法是由R.C.Eberhart 博士和J.Kennedy 博士提出的一种仿生智能的全局优化算法［16～17］。种群中的个体称为粒子，粒子具有简单的行为规则，从而使种群表现出复杂的特性。粒子根据自身经历过的最优位置和种群经历过的最优位置更新位置和速度，经过多次迭代搜索解出空间的最优解，用于求解复杂的优化问题［18］。

在d 维搜索空间中，P={p1，p2，…，pM}表示由M 个粒子组成的种群，向量xi={xi1，xi2，…，xid}和vi={vi1，vi2，…，vid}分别表示粒子pi的位置和速度。粒子pi经历过的最优位置记为pbesti，而种群经历过的最优位置记为gbest。粒子pi根据pbesti和gbest，利用式（4）和（5）更新自己的位置xi和速度vi。

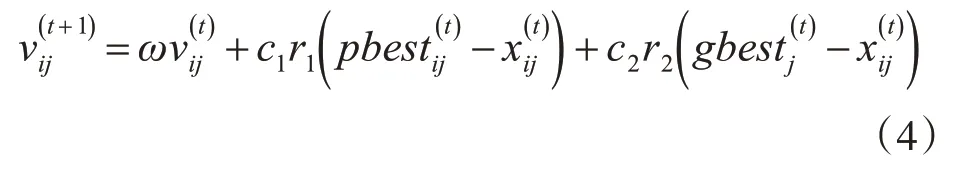
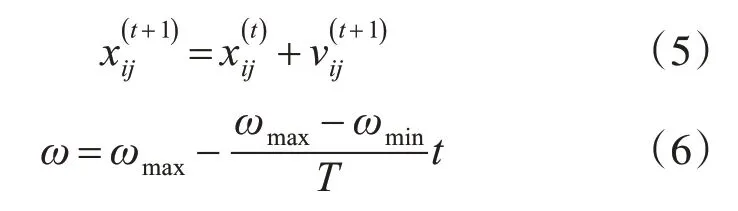
其中t 为当前迭代次数，T 为最大迭代次数。学习因子c1、c2取值都为2［19］，r1、r2为区间［0，1］上的随机数。ω为惯性权重，采用文献［20］提出的线性递减策略动态调整惯性权重策略，其中ωmax和ωmin分别是ω的最大值和最小值，根据文献［21］，本文取ωmax=0.9，ωmin=0.2。此外，为了防止粒子飞出解空间，设定速度的边界值Vmax。

3.1 离散与编码

移动云计算的任务调度是组合优化问题，粒子的位置和速度要用离散的方式表示，而PSO算法是基于连续空间的优化问题，导致粒子的位置不能按照式（4）和（5）进行更新［22］。为使PSO 算法能够在离散组合优化问题中得到有效应用，本文采取一种基于任务自然数的编码方式，编码长度取决于任务数量，如n任务m移动设备的调度问题，用n维向量编码{c1，c2…，cn} 表示粒子的位置，编码的第i维分量ci∈{1 ，2，…，m} ，表示将任务ti分配到移动设备dci上执行。

使用编码的方式可以将PSO 算法应用于求解离散空间组合优化问题，按照式（4）和（5）更新后的粒子位置向量可能不符合本文提出的编码，则可以如下方法对更新后的粒子位置向量进行再调整：给出 一个粒 子位置 向 量x={x1，x2，…，xn} ，如 果xi∈[-m，0 )∪(0 ，m]，则 更 新如果xi∈(- ∞，-m)∪(m，+∞ )，则更新如果xi=0，则更新xi为{1 ，2，…，m} 上的随机值。

3.2 适应度

本文采用总完成时间FT 作为粒子的适应度，同时考虑移动设备的电池容量的约束。适应度作为优化的目标，可以作为粒子的评价标准，粒子的适应度越小，越容易被选择作为潜在的最优解。粒子的适应度计算方法如算法1所示。

算法1 粒子适应度的计算方法

输入 移动云计算的DAG 任务图，粒子的位置编码x，网络带宽（bps），移动设备网络（处理性能、电池容量等）

输出 粒子的适应度FT

step1 计算DAG图中每个任务的高度height'；

step2 为所有任务建立队列；

step3 按照height'递增的顺序对任务队列排序，height'相同的则按照任务编号递增排序；

step4 如果任务队列非空，转到step5；否则，转到step10；

step5 从任务队列的头部取出一个任务为tk；

step6 根据粒子位置编码x 将任务tk分配到移动设备dxk上执行；

step7 计算tk在dxk上的执行所需时间，记为time；

step8 tk获得设备的时间记为GainTime，经过Delay 时间的通信延时，tk获得所有的依赖数据，则tk的完成时间为GainTime+Delay+Time（如果存在依赖关系的任务在相同移动设备上执行，则通信开销cost=0 ；否则cost=通信量/bps。Delay=max(costi)）；

step9 tk执行完成后，从任务队列中删除tk，转到step4；

step10如果所有移动设备的电池容量可以满足在其上执行任务消耗的电量，转到step11；否则转到step12；

step11输出所有的移动设备中最后一个任务的完成时间，转到step13；

step12输出∞，转到step13

step13算法结束。

3.3 PSO求解任务调度问题

PSO 算法将任务高度height'，使用算法1 的方法作为粒子的适应度函数，使用全局模型进行粒子更新，最优粒子为适应度最小的粒子。PSO 求解移动云计算任务调度问题的过程如算法2所示。

算法2 PSO求解任务调度问题

输入 移动云计算的DAG 任务图，网络带宽（bps），移动设备网络（处理性能、电池容量等），粒子数

输出 全局最优的调度方案

step1 计算DAG图中每个任务的高度height'；

step2 初始化PSO 的相关参数，设置最大迭代次数T和当前迭代次数t=0；

step3 使用离散编码的方式，初始化种群粒子的位置为{1 ，2，…，m} 中的随机值；初始化种群粒子的速度为[-Vmax，Vmax] 上的随机数；

step4 计算种群中每个粒子pi的适应度FT(pi)；

step5 如果FT(pi)＜FT(pbesti)，转到 step6；否则，转到step7；

step6 粒子pi当前位置xi为自身经历过的历史最优位置，更新pbesti=xi；

step7 如果FT(pi)＜FT(gbest)，转到step8；否则，转到step9；

step8 粒子pi当前位置xi为种群的历史最优位置，更新gbest=xi；

step9 根据式（4）和（5），更新粒子位置xi和速度vi；

step10t=t+1；

step11如果t小于T，转到step4，否则转到step12；

step12输出gbest；

step13算法结束。

3.4 迭代局部搜索

在调度问题中，PSO 算法的优化过程都是从初值出发，求解初值所在邻域的极值，存在着过早收敛，搜索精度不高等缺点，容易陷入局部最优解，无法保证是解空间的最优解［23］。为了避免算法陷入局部最优，则需要提出一种扰动策略，为搜索找到新的方向。

迭代局部搜索（Iterated Local Search，ILS）是一种元启发式算法，为局部搜索策略提供简单、强大而高效的框架，成功地应用于TSP 问题，车间调度和背包问题等领域［24］。ILS使用PSO搜索到的最优解作为当前解，通过扰动到当前解的邻近区间寻求更优的解更新当前解，直到无法改进为止，作为近似全局最优解，这是一种可行的全局优化方案。

交换是最常用的扰动策略，分为邻位交换和一般交换。邻位交换是指将粒子位置编码的第i个和i+1个分量互换；一般交换是指将粒子位置编码第i个和j个分量互换（i≠j）。一般交换的方法可能扰动作用过于强烈，所以本文采用邻位交换的扰动方式。

将迭代局部搜索应用于任务调度问题，最大未改进次数（MAX_UNMODIFIED_COUNT）是最常用的终止条件。根据文献［25］，考虑将最大未改进次数设为80，最终可以得到更好的解。

将PSO 算法作为ILS 局部搜索方法，求解移动云计算任务调度问题的过程由算法3给出。

算法3 ILS-PSO求解任务调度问题

输入 移动云计算的DAG 任务图，网络带宽（bps），移动设备网络（处理性能、电池容量等），粒子数

输出 全局最优的调度方案

step1 计算DAG图中每个任务的高度height'；

step2 初始化PSO 和ILS 的相关参数，最大迭代次数T和最大未改进次数MAX_UNMODIFIED_COUNT；

step3 初始化当前未改进次数k=0；

step4 使用离散编码的方式，初始化种群粒子的位置为{1 ，2，…，m} 中的随机值；初始化种群粒子的速度为[-Vmax，Vmax] 上的随机数；

step5 执行PSO搜索，搜索结果gbest赋值给sbest；

step6 k ＜ MAX_UNMODIFIED_COUNT，则转到step7；否则，转到step12；

step7 使用邻位交换的方法对粒子的位置编码进行扰动；

step8 执行PSO搜索，结果gbest赋值给slocal；

step9 如果FT(slocal)＜FT(sbest)，转到step10；否则，转到step11；

step10sbest=slocal，k=0，转到step6；

step11k=k+1，转到step6；

step12输出sbest；

step13算法结束。

4 实验与分析

本文采用CloudSim作为仿真环境，对移动云计算任务调度问题进行仿真，实验环境为Microsoft Windows 7 专 业 版 、Intel Core i7-6700 3.40GHz、8.00G RAM、CloudSim-3.0.3、Eclipse。

参数设置：

1）PSO的相关参数：c1=2，c2=2，r1、r2为区间［0，1］上的随机数，ωmin=0.2 ，ωmax=0.9 ，Vmax=1。

2）ILS 的相关参数：最大未改进次数设置为MAX_UNMODIFIED_COUNT=80。

3）移动云计算的设备网络由5 个移动设备构成，网络带宽bps=1，移动设备的处理性能和可提供给任务的最长可执行时间（即电池容量/功率）如下所示：

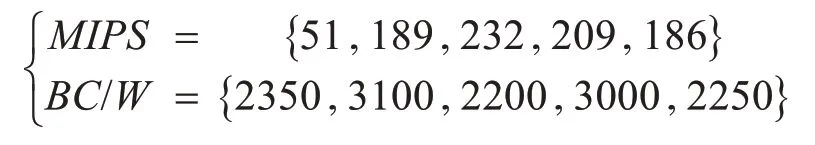
实验设计：

1）粒子数为100，任务数为100，最大迭代次数为100，观察随着当前迭代次数的增加，PSO优化性能的变化。

2）粒子数为100，任务数为100，最大迭代次数从0 递增到100，观察最大迭代次数对PSO 和ILS-PSO寻优的影响。

3）最大迭代次数为100，粒子数为100，任务数从0 递增到300，观察轮转算法（RR），贪心算法（Greedy）、PSO 和 ILS-PSO 求解不同数目的任务调度问题的性能差异。

本文采用文献［26］的方法，根据任务数随机生成DAG 任务图，任务的长度为[2 0000，30000] 上的随机整数。每个实验重复20 次，实验结果取平均值来降低误差。

实验1结果如图1所示。可以看出PSO具有优化性能好、快速收敛的优点，然而迭代进行到了40次左右的时候，优化陷入了局部最优解，随着迭代次数的增加，搜索性能不再有明显变化。

实验2 结果如图2 所示。由实验1 的结果可以，迭代次数到达45 次左右时，PSO 算法进入局部最优，所以最大迭代次数小于45 的时候，随着最大迭代次数的增加，PSO 搜索性能持续提升；当最大迭代次数接近并且超过45 的时候，PSO 搜索性能提升缓慢直到不再有明显变化。对于ILS-PSO 算法，当PSO 搜索陷入局部最优时，通过多次扰动到临近区间迭代求解更优解，求解出近似全局最优解。

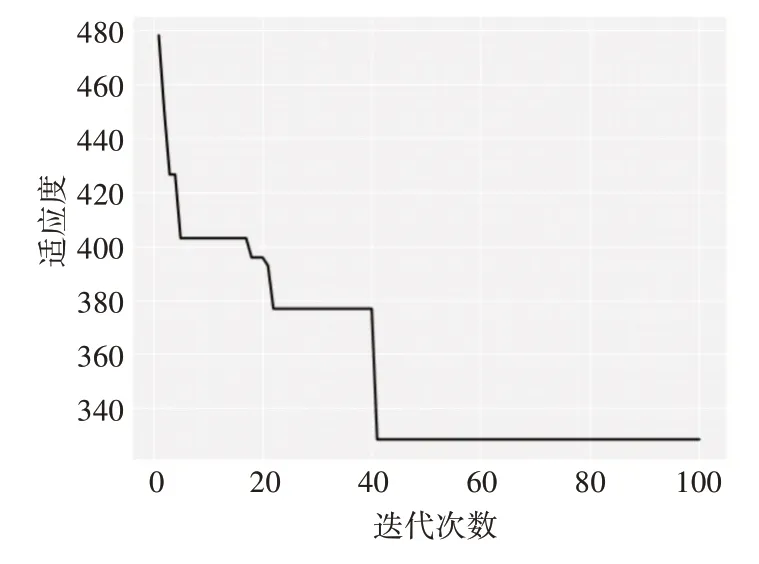
图1 实验1的结果

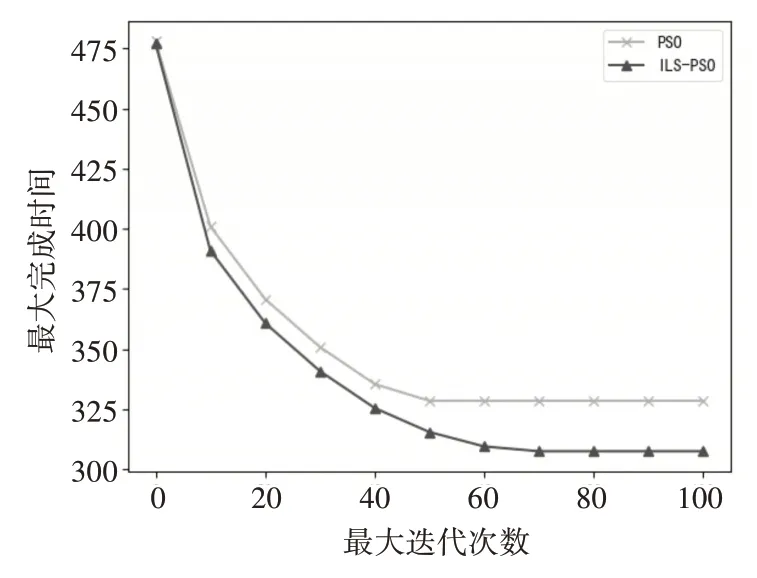
图2 实验2的结果

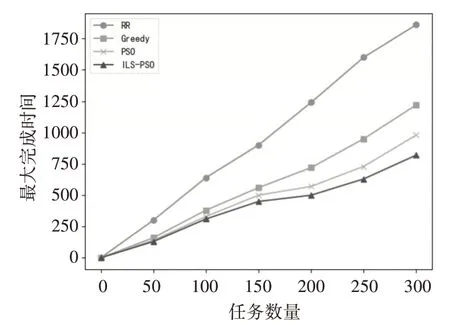
图3 实验3的结果

实验3 的结果如图3 所示。可知PSO 和ILS-PSO 在初期搜索优势并不明显，这是由于任务数量较少时，DAG 图的复杂程度较低，可以使用Greedy 算法求解出较好的结果。随着任务数量的增加，DAG 图的复杂程度剧增，可以看出RR 和Greedy 的最大完成时间与任务数量近似成正比。由于存在迭代搜索过程，在中后期PSO 和ILS-PSO的搜索效果明显优于RR 和Greedy，同时ILS-PSO为防止PSO搜索进入局部最优应用了扰动策略，迭代搜索出近似全局最优解，所以ILS-PSO 的搜索性能优于PSO，并且随着问题复杂程度的增加，优势更加明显。

在三种情况下进行仿真实验，结果表明了本文所提出的ILS-PSO 调度算法可以有效提高移动云计算环境下的系统处理调度问题，减少了总任务的完成时间，提高了移动设备的利用效率，在时间性能和优化性能上取得了较好的效果。

5 结语

异构移动设备网络和移动设备的电池容量限制是影响移动云计算环境下任务调度执行效率最具有挑战性的关键因素。本文分析了当前移动云计算任务调度的研究现状和移动设备存在的客观约束的基础上，提出了适用于异构移动设备网络下的DAG 任务图的ILS-PSO 算法求解全局最优调度方案。通过位置编码的方式，将连续空间的优化问题和离散空间的调度问题联系起来，将任务高度作为任务的优先级，PSO 算法作为搜索方法，从而得到高效的调度方案，提高了资源利用率，也缩短了程序的完成时间。为防止PSO搜索陷入局部最优，应用迭代局部搜索策略，通过扰动方法到局部解的邻近区间寻求更优解更新当前解，最终找到近似全局最优解。最后通过实验仿真，验证了本文提出的ILS-PSO算法的有效性。