Meta分析模型及其应用

刘瑞银, 畅艺婷

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

Meta分析是对某一特定问题的诸多研究结果进行综合评价的一种统计方法,1976年由Glass首次命名为meta分析,并将其定义为以综合已有的研究结果为目的,对单项研究结果进行综合的统计学方法。Meta分析最早被应用于教育学等社会科学领域,20世纪90年代开始被广泛应用于自然科学领域[1-6]。

假设研究的总体为X～F(x;μ,σ2),其中均值μ为感兴趣的总效应量。现有K个调查小组对该问题进行调查研究,得到了K组样本x1,x2,…,xK,其中

每一组的样本均值记为ti,又称作子效应量。样本均值ti的误差记为vi,其中i=1,2,…,K。Meta分析指的是,在不知道原始样本x1,x2,…,xK,只知道由原始样本估计的子效应量ti及子效应量的误差数据vi的情况下,如何对效应量μ进行估计。

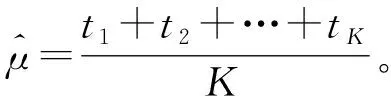
这里需要特别注意的是,研究中感兴趣的效应量不一定是均值,而是根据实际情况而定的统计量。在本文中,不加注明的话,假设是均值。

1 Meta分析

Meta分析根据所建立模型的不同可以分为固定效应模型和随机效应模型。下面分别介绍meta分析的这2种模型,并对它们进行比较。

1.1 固定效应模型

在固定效应模型下,假设所有的研究都来自于同一个总体[8],那么它们估计的效应量μ是相同的,也就是说μ1=μ2=…=μK=μ,实验数据来自均值为μ方差为σ2的分布,即xij～F(x;μ,σ2),观测效应Ti的分布为Ti～F(x;μ,vi)。在这种模型下只有一种误差即组内误差。如图1所示,总体是均值为μ方差为σ2的分布,观测效应为Ti,ei为随机误差,也就是组内误差,观测效应Ti的表达式为

Ti=μ+ei

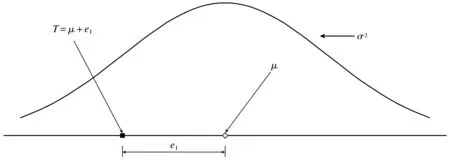
图1 固定效应模型Fig.1 Fixed effect model

研究中通常用样本量来作为权重,例如携带1 000个个体的研究得到的权重会是携带100个个体的研究的权重的10倍。但是这种方法并不精确,因此meta分析提出运用每组研究的方差的倒数来作为每组研究的权重[9],也就是说第i个研究的权重wi为

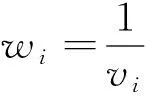
(1)

其中vi为第i组研究中子效应的方差。

Meta分析的计算方法及步骤如下[10-12]:

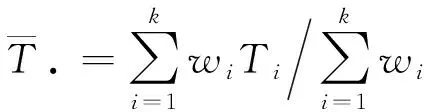
(2)

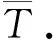
联合效应的方差为权重和的倒数,表达式为

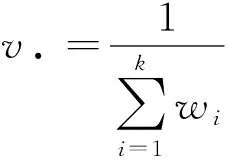
(3)

推导过程如下:

联合效应的标准误差为

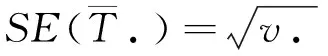
(4)

则95%的置信区间为

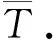
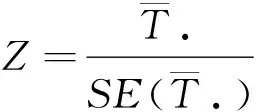
(6)

单尾检验p值为

p=1-Φ(|Z|)

(7)

双尾检验p值为

p=2[1-Φ(|Z|)]

(8)

其中Φ为标准正态分布的分布函数。

1.2 随机效应模型

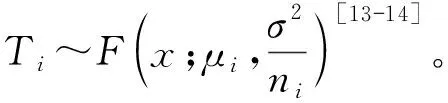
Ti=μ+εi+ei

其中:εi为组间误差;ei为组内误差。

图2 随机效应模型Fig.2 Random effect model

随机效应模型将误差分为2个部分,组内误差和组间误差,当分配权重的时候也是运用这2个部分来计算,这样会更加精确。设总方差为Q,其公式如下

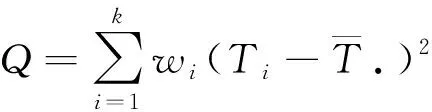
(9)

它是由组内方差和组间方差相加得到的,如果方差的来源只有组内方差,那么Q的期望值就会等于自由度df,其中

df=(NumberStudies)-1

证明如下:

其中

带入(10)式得

其中总方差Q减去自由度df得到的是额外方差,也就是组间方差,记为τ2,其表达式为

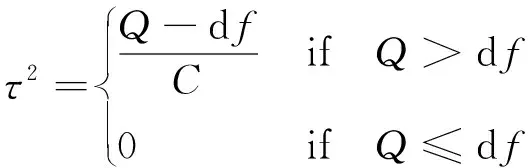
(11)

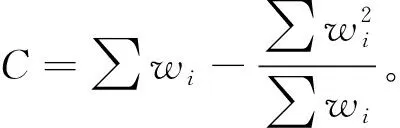
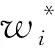
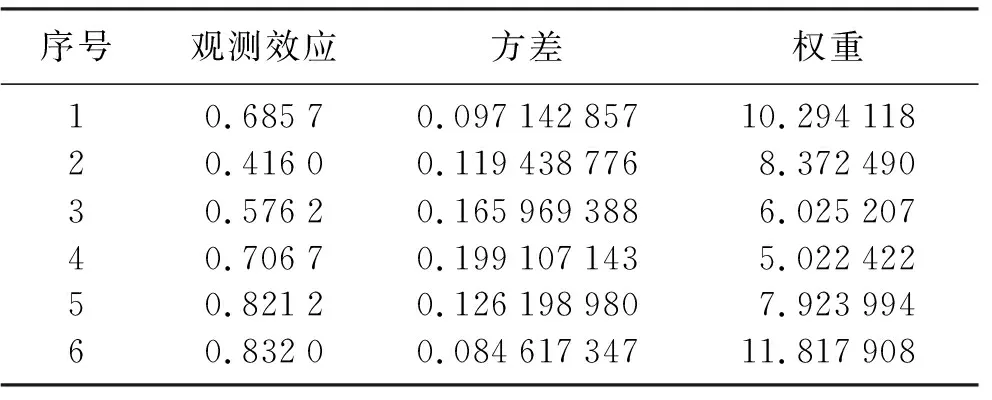
表1 植物种群密度和植物质量对植物代谢率的影响

由于随机效应模型的计算公式与固定效应模型的形式一致,这里不再重复。

2 实例分析

表1是2012年统计的植物种群密度和植物质量对植物的代谢率的影响[16],其中原假设为植物种群密度和植物质量对植物的代谢率无影响,备择假设为植物种群密度和植物质量对植物的代谢率有影响。

若将该研究模型看作固定效应模型,利用R语言进行计算,每一组的权重可以根据式(1)给出,根据式(2)到式(8)其他计算结果为

v=0.020 2

LowerLimit=0.678 6-1.96*0.142 2=0.399 9

UpperLimit=0.678 6+1.96*0.142 2=0.957 3

P1T=1-(Φ(|4.772 4|))<0.000 1

P2T=2[1-(Φ(|4.772 4|))]<0.000 1

由于2个p值都小于0.000 1,所以拒绝原假设,也就是说有理由相信植物种群密度和植物质量对植物的代谢率有影响。

若将其看做随机效应模型,由式(9)得到总方差Q的值为

因该模型自由度为5,大于总方差Q,由式(10)知,组间方差τ2为0,所以该模型为固定效应模型。

3 结 语

因固定效应模型假定所有研究都来自一个总体,即影响每个研究的效应的元素是相同的,所以估计值也就是联合效应是相同的,模型误差仅来自于每个研究固有的随机误差,即组内误差。但随机效应模型假定每个研究来自不同总体,所以得到的是一个分布,估计值是分布的均值,模型的误差不仅来自于组内误差,还来自于研究与研究间的组间误差。另外,在处理一些比较极端的实验时,固定效应模型会忽视一些比较小的研究,但是随机效应模型不会,因此随机效应模型的权重会比固定效应模型平衡一些。

因此当选择固定效应模型来进行计算时,有理由相信所有研究的功能是相同的,研究的目的是计算共同的效应然后将其推广到其他相同总体的例子中。如选择随机效应模型,由于数据来自前人研究,所以研究功能不同,这些研究对象或干预可能会对结果有影响,对此研究目的是将其推广到一系列不同总体中。但如研究数量较小,不太可能精确估计组间误差,所以此时选择固定效应模型。