基于多基因遗传规划的储层岩石静态模量预测*

王文文 李 诺 韩建强 罗 涛 肖 涛

(1 中海油田服务股份有限公司油田技术事业部 北京 101149)

(2 中国科学院大学 北京 100049)

(3 北京市海洋深部钻探测量工程技术中心 北京 100190)

(4 中国电子科技集团公司第三研究所 北京 100015)

(5 中国石油渤海钻探工程有限公司工程技术研究院 任丘 062550)

0 引言

掌握岩石的力学性质有助于解决众多地球科学、岩土工程等领域的问题，特别是在石油和天然气的勘探和开发领域。杨氏模量是最常见的力学参数，这些参数可以从岩石压缩测试(也称静态测量)中测量的应力-应变关系中获得。但是静态测量实验装置复杂，对人员的操作要求高，其过程通常十分耗时而且测试费用昂贵，因此在井中的整个深度区间实施连续取心以获得岩石力学参数的连续剖面是不现实的，但该剖面在分析井壁稳定性、出砂、压裂等方面至关重要[1]。实验室弹性波速度的动态测试相对来说十分高效，而且成本很低，一般利用超声波脉冲传输法测量纵波和横波速度来计算动态弹性性质[2]。在现场，也可以利用地震勘探或声波测井得到的地震波或声波速度来获得深度连续的动态弹性剖面[3]。

由于储层岩石复杂的孔隙结构，并且孔隙空间通常含有流体，其动态和静态性质之间往往存在很大差异[4]。通常对实验室测量的少量岩心的动静态数据进行统计分析，利用拟合方法(一般是线性拟合)得到二者的经验关系，以此对现场的动态数据进行校正来得到静态性质[5]。然而，由于信号衰减较大，计算岩石动态性质的必要参数——横波速度在实验室中往往难以测量；而在测井中，由于声波测井方法和地层性质的限制，横波速度也难以获得[6-7]。这些限制使得动态、静态性质的转换问题更加复杂。此外，在回归建模中，需要用有限的参数和方程预定义经验模型的结构，现有的经验关系存在精度较低、适用性不高的问题。为了克服这些局限性，提出一种高精度的方法，从有限的测量数据中预测岩石静态性质。

近年来，人工神经网络、模糊推理系统等人工智能方法已经用于解决此类问题[8]，但是它们仅适用大数据集，同时不能提供静态性质预测的解析表达式[9-10]。本文提出一种基于多基因遗传规划(Multi-gene genetic programming，MGGP)的储层岩石静态性质预测方法，可以不需要先验信息建立预测方程。首先，介绍了动态和静态模量的定义及其区别的内在原因。其次，描述了MGGP算法的特点和流程。最后，通过一组实验数据分别研究了线性拟合和MGGP 在静态模量计算中的应用。

1 静态和动态杨氏模量

静态杨氏模量是从单轴压缩测试中获得的应力-应变曲线直线段的斜率，所谓单轴压测试，指的是圆柱形样品在无侧向围压下承受端部平面上的力。值得注意的是，由于岩石具有非均质、非线性的特点，其应力-应变曲线并不是一条直线，由此可按照斜率的不同定义3 种模量：切线模量、割线模量和平均模量。本文讨论的是平均模量及应力-应变曲线近似直线段的斜率，在此段微裂隙完全闭合，可以认为岩石发生的是线弹性变形。此时静态杨氏模量Esta定义为轴向应力增量Δσz与轴向应变Δεz的比值：

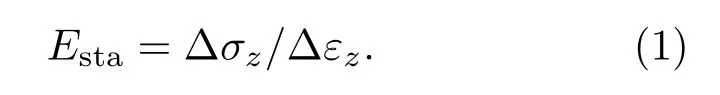
实验室通常采用超声脉冲透射法测量样品的纵横波速度，根据弹性波传播理论，动态杨氏模量Edyn定义如下：

其中，ρb是体密度，VP和VS分别为纵横波速度。

储层岩石由于具有复杂的孔隙结构，静态加载过程中应力加载速率较慢，可以近似为0 频，变形幅度较大(＞10-4)，变形包括弹性和非弹性成分[11]。而在动态测量中，由于频率较高，岩石只承受瞬时应力，而且变形幅度很小(＜10-6)，测量过程中的变形可以看作是弹性的。如果岩石饱和流体，由于作用频率的差异导致静态测量过程中孔隙压力处处平衡，动态测量过程中岩石处于不排水状态，孔压不平衡，情况更加复杂[12-13]。因此，无论是实验室超声透射法还是现场声波测井方法，得到的动态模量都与岩石的静态模量都会有差异，甚至差异较大。

2 多基因遗传规划

遗传规划(Genetic programming，GP)是由Koza[14]提出的一种进化算法。与遗传算法(Genetic algorithm，GA)类似，GP 以达尔文进化论为基础，借鉴了生物界的自然选择和遗传机制。在一个由多个个体组成的群体中，每个个体都代表一个可行的解，通过选择、复制、交换、变异等遗传操作，根据最优适应度逐步迭代，得到最优解。然而不同于只能对字符串进行操作的GA，GP是一种符号回归方法，可以对树状结构的计算机程序进行操作，将输入与输出以解析方程的形式联系起来。多基因遗传规划(MGGP)是GP 的变体，结合了GP 的模型构建能力和统计回归方法的参数估计能力[15]。在传统的遗传规划中，进化模型由一棵树组成，而在多基因遗传规划中，每一个回归模型都是多棵树的加权线性组合。利用MGGP 进化得到的模型结构示例如图1所示，函数集和符号集分别构成树的节点和叶。在图1中，函数集包括“log，+，×，sin”，终止符集包括“A，x1，x2”，d0是偏置项，d1和d2是权重系数。与GP 相比，MGGP 能够使预测模型具备非线性特征，从而具有更高的精度和效率[15-16]。

图1 利用MGGP 进化的一种典型模型结构Fig.1 A typical structure of model evolved by MGGP

图2给出了MGGP的工作流程，可以概括如下：

(1)随机产生初代种群，包含一组由函数和变量组成的个体；

(2)计算种群中每个个体的适应度；

(3)选择适应度好的优良个体为母体；

(4)通过突变、交叉、复制等方式产生新的个体，创造新的一代(子代)；

(5)重复步骤(2)和步骤(3)，直到满足终止准则。

图2 MGGP 算法的一般流程Fig.2 The general workflow of MGGP algorithm

用于评估模型的适应度函数是实际值ydata和预测值ypre之间的均方根误差(Root mean square error，RMSE)：

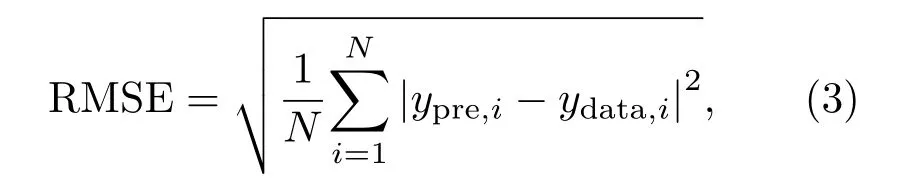
其中，N为参与评估的样本数目。用相关系数R来表示测量值与预测值之间的相关关系密切程度，即两个变量之间的协方差和两者标准差乘积的比值。

3 实验测量与结果

实验中，共对32 块井下取心的砂岩样品进行实验测量与分析，相关实验在中国科学院声学研究所的高温高压岩石动静态三轴实验系统GCTS RTR-2000 进行，如图3所示。该装置包括主钢架、压力控制器、超声波控制器等，能满足样品干燥和饱和态下的声学和力学参数测量。该系统最大作用力2000 kN，内置精度为0.15%的载荷传感器，能够进行轴向应力加载；仪器配置有围压孔压加载装置，最大加载量140 MPa，精度为0.25%，可以进行围压加载；实验中轴向应变加载速率为每秒0.001%，一分钟测量一次；采用量程±3 mm的线性可变差动变压器(Linear variable differential transformer，LVDT)变形传感器测量应变，精度为0.25%。静态杨氏模量Esta是应力-应变曲线在30 MPa～35 MPa的应力区间段内的拟合直线斜率，因为在该应力区间内曲线近似为一条直线，可认为岩石发生线弹性变形，见图4。采用超声脉冲透射法测量了相同应力范围内的纵波速度VP和横波速度VS，结果取为整数，单位为m/s。

图3 GCTS RTR-2000 岩石力学三轴测试系统Fig.3 The GCTS RTR-2000 rock mechanic triaxial test system

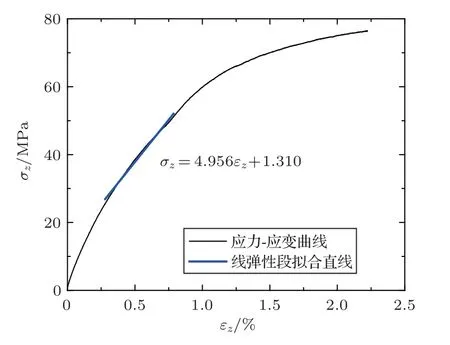
图4 一块岩心样品的单轴应力-应变曲线Fig.4 Stressstrain curve of a core sample

用作为完全弹性体的标准铝样进行测试，得到系统测量误差如下：(1)应力应变测量误差为0.25%；(2)纵波速度测量误差为0.52%，横波速度测量误差为0.77%；(3)动态模量测试误差为1%，静态模量测试误差为0.5%。

结合测量的体密度ρb，用式(2)计算动态杨氏模量Edyn，结果保留小数点后两位，单位为GPa。通过SCMS-C3 型覆压孔渗测量仪测得样品孔隙度φ，结果保留小数点后四位。所有测量结果在表1中给出，前30块样品为饱和测量结果(-S表示)，后30 块样品为干燥测量结果(-D表示)。由于测量过程中信号的强衰减，其中4 块饱和样品和1 块干燥样品的横波信号由于信噪比较低，没有获得可靠的测量值。而且样品31 和32 在干燥测量后，样品出现明显裂隙，没有进行饱和测量。

表1 样品参数测量结果Table1 Parameters measurement results of samples

绘制干燥和饱和条件下的动静态模量交会图如图5所示。动态杨氏模量Edyn和静态杨氏模量Esta之间存在较好的线性相关性，通过线性拟合得到二者之间的线性关系：

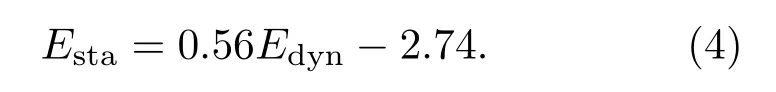
图5 干燥和饱和样品的动静态模量Fig.5 Dynamic Young’s modulus compared to static Young’s modulus of dry and saturated rocks

4 MGGP预测

在MGGP 方法中，静态杨氏模量为待预测参数，而终止符集中的体密度、孔隙度和纵波速度是预测参数，函数集包含运算符“+、-、*、/、sqrt、ln(x)、log(x)、exp(x)、abs(x)、square、cubic、power、sinh(x)、cosh(x)、sin(x)、cos(x)”。终止符集和函数集用来构建MGGP 模型。随机选取70%的数据进行模型的训练，其余30%的数据进行测试。表2列出了构建杨氏模预测模型所用的MGGP 模型参数。

表2 预测静态杨氏模量的MGGP 模型参数Table2 MGGP model parameters used to predict static Young’s modulus

在进化300 代之后适应度函数均方根误差RMSE 值为3.44，得到了一个关于孔隙度φ、体密度ρb和纵波速度VP的静态杨氏模量方程：

为了验证式(5)的效果和适用性，将MGGP 预测的结果和动态数据标定值(式(4))分别与实际测量值进行了比较，结果如图6和图7所示。在训练集和测试集中，MGGP 模型都能有效地预测杨氏模量，训练集的相关系数为0.865，测试集的相关系数为0.726。对于线性拟合方程预测结果，5 块样品由于横波速度缺失而缺少经验预测值(在图中显示为0 值)。除去缺少数据的5 块样品，线性拟合结果与测量值的相关系数为0.829。由此可见，与利用动态数据得到的线性模型相比，MGGP 训练集中预测的杨氏模量更接近实测静态值，并且对于测试集也有很高的精度，同时避免了横波数据缺失无法直接计算的影响。

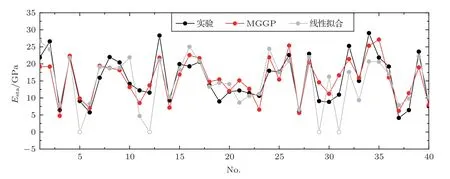
图6 训练集线性拟合、MGGP 模型静态杨氏模量预测值与实验测量值对比Fig.6 Static Young’s moduli from experiment，linear fit and MGGP in training set

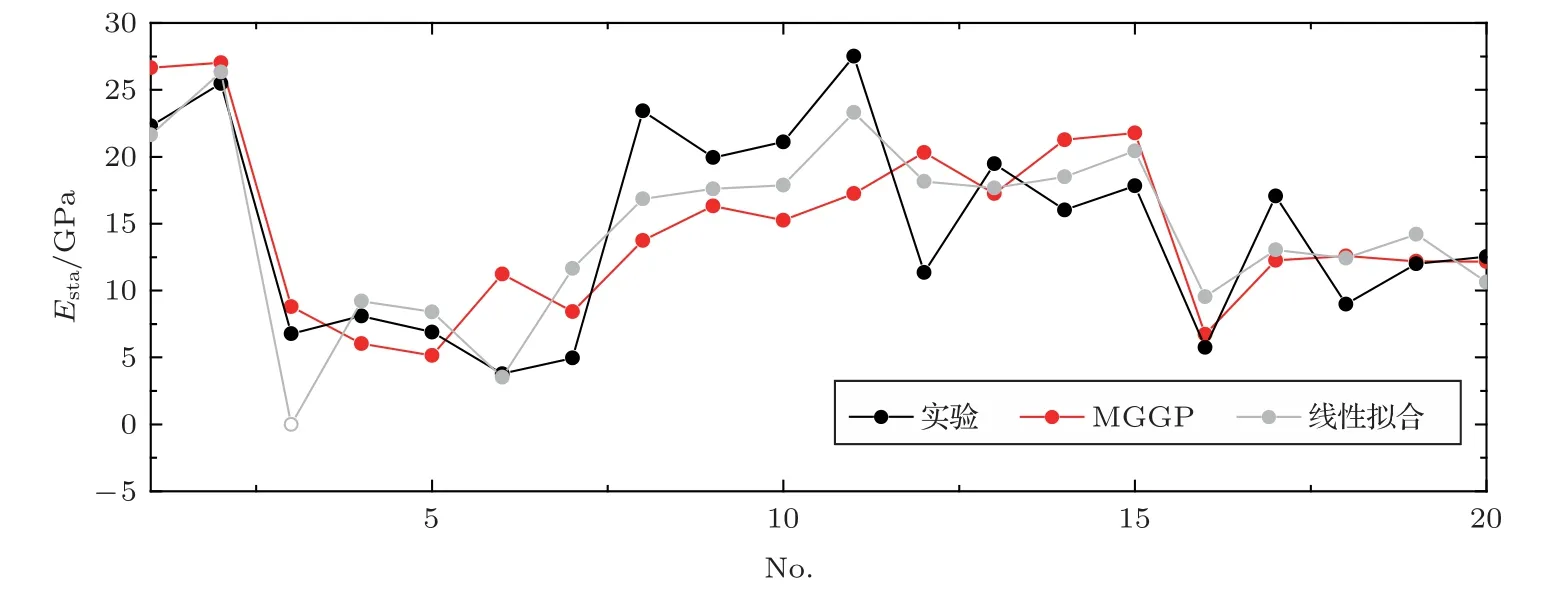
图7 测试集线性拟合、MGGP 模型静态杨氏模量预测值与实验测量值对比Fig.7 Static Young’s moduli from experiment，linear fit and MGGP in testing set

5 结论

本文采用MGGP 方法对储层砂岩样品的静态杨氏模量进行了预测。该模型比用动态数据线性拟合标定的经验关系有更好的适应性。此外，在缺失横波速度的情况下，它也能够利用较少的输入参数，即孔隙度、体积密度和纵波速度来进行预测，从而减小了横波波速度不准确或丢失所引起的计算误差。结果表明，MGGP 在实验中用来预测静态杨氏模量是可行的，这为现场数据(测井或地震)在解决岩石力学问题提供了更好的数据处理手段。