应用支持向量机和人工神经网络对大气次声信号识别的初步实验

吴涢晖 邹士亚 庞新良 陈晓雷

(防化研究院 北京 102205)

0 引言

将核爆炸或自然界事件信号从背景噪声中提取出来，然后对事件信号进行分析识别，是核爆监测的基本内容之一。事件信号提取的方法主要是首先通过滤波的方法降低噪声的干扰，然后采用信号检测算法或人工的方法提取事件数据[1]。这些方法都需要根据实际噪声和信号的特点设置相应的阈值，来对信号进行检测，而阈值的设定则依赖于研究人员对信号的分析结果或者经验，需要花费大量的时间针对每一个不同的环境进行研究。即便如此，仍然会不可避免地将噪声检测为事件。

随着核爆次声监测网络的建设，大量的实时监测数据将源源不断地发送到数据处理中心，对这些监测数据的实时分析需要一种有效的技术方法来支持，而机器学习的快速发展为解决这个问题提供了有效的手段，其中基于仿生学的人工神经网络(Artificial neural network，ANN)和基于统计学习的支持向量机(Support vector machine，SVM)在解决实际问题中表现出良好的性能。

ANN作为一种通用的模式分类器，其泛化能力取决于样本的选取和模型的结构与参数，在实际应用中不需要太多先验知识，但需要经过大量的实验摸索，才能确定合适的神经网络模型以及相关参数的设置，其分类效果与样本数量具有很大关系，需要对模型不断优化来防止过拟合。

SVM是一种基于统计学习理论的分类方法，它从理论上系统地研究了有限样本下经验风险与期望风险的关系，能较好地解决小样本问题，通过将样本特征映射到高维空间，解决了非线性不可分的问题，并利用内积核函数巧妙地解决了高维空间中计算复杂度剧增的问题；但对于大规模训练样本，SVM需要耗费大量的机器内存和运算时间。

本文对次声台站的单通道数据进行了信号检测，采用ANN 和SVM 对信号和噪声进行了分类实验，对比分析了两种方法对次声事件的自动识别能力，研究探索了提高它们的识别能力的方法，以期能有效地应用到实际工程中去。

1 次声信号检测

次声波信号作为一种低频声信号，极易受到背景风和其他大气噪声的影响。在进行事件识别前，首先要对次声信号进行检测，提取出疑似事件的数据。在实际应用过程中，已经研究出一些经典的检测方法，如基于F-统计的Fisher 检测算法[2]、互相关算法[3]、短时窗平均/长时窗平均(Short term averaging/long term averaging，STA/LTA)算法、逐次多通道互相关(Progressive multi-channel correlation，PMCC)检测算法[4]等。本文采用国际数据中心使用的STA/LTA 算法，从次声传感器记录的数据中检测出可能的事件信号。

STA/LTA 方法是由Stevenson 提出，最先应用于地震监测中，用来判定地震初至波的到达时间，其基本原理为：用STA(短时窗平均值)和LTA(长时窗平均值)之比来反映信号幅度、频率等特征的变化。当有事件信号到达时，STA/LTA值会发生突变，通过设定一个阈值R，根据当其比值是大于R或者小于R来判定为事件信号或是噪声[5-6]。R的计算公式为

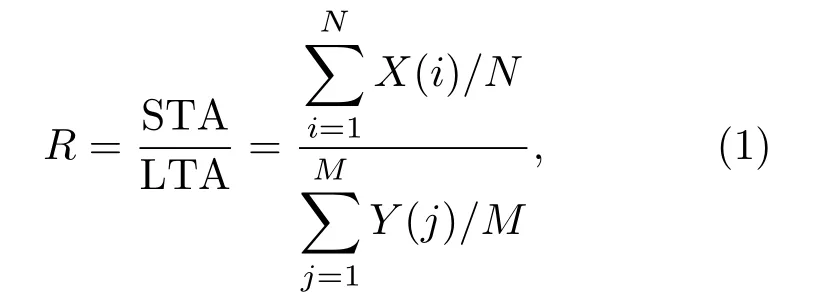
式(1)中，X(i)(i=1，2，···，N)表示短时间窗内数据；Y(j)(j=1，2，···，M)表示长时间窗内的数据；M和N分别表示长、短时间窗内的样本数。如果R大于设定阈值，则认为该数据包含事件信号。

在实际中，检测阈值无法精确地给出，即使假设次声传感器记录的数据只包含背景噪声，此阈值也可能随着时间发生变化。当选择不同的阈值时，检测出的信号数量也大不相同，如图1所示。图1中对节选的2000 个数据点(采样速率为100 sps)的次声波形进行分析，当R= 2 时，检测出信号的数量为18次；当R=3 时，检测出信号的数量为6 次；当R=4.5时，检测出信号的数量为2次。

可以看出，阈值的选取对信号的检测有较大影响，好的阈值可以过滤掉大部分的无用数据，减轻后期数据分析的负担。当检测阈值设置过高时，采用STA/LTA 算法的Libinfra 软件检测率只有41.18%(PMCC 算法的检测率为94.12)[3]。但是，无论如何选取阈值，在长时间的监测过程中，都会产生大量的“事件信号”，需要进一步对这些信号进行识别。

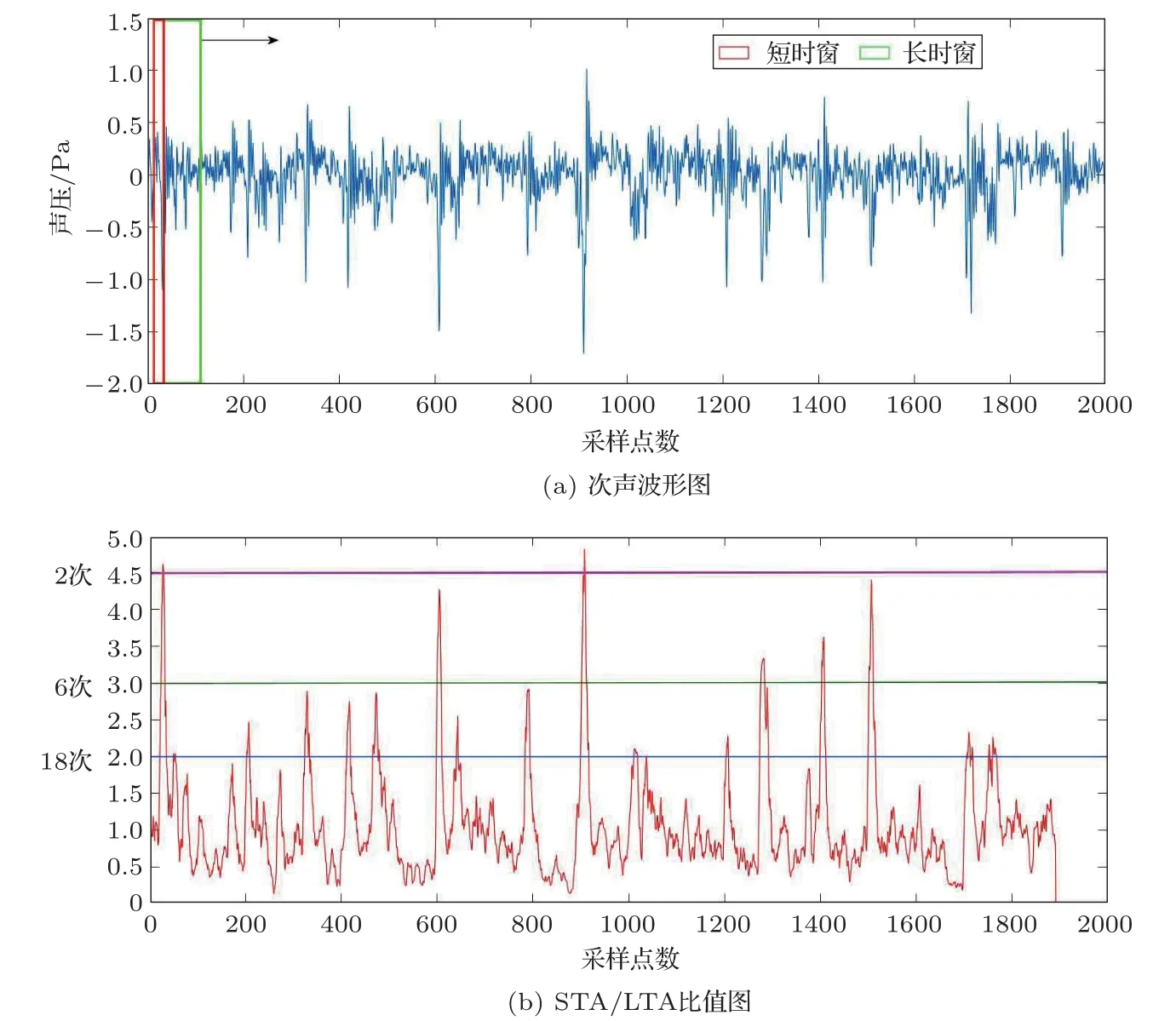
图1 R对信号检测的影响Fig.1 The effect ofRon effective signal detection

2 基于小波包分解的信号能量特征

信号的特征主要包括时域特征、频域特征和时频联合域特征。时域特征包括信号的均值、方差、均方根、最大最小值、峭度、脉冲因子、波形因子等，是对信号变化描述最基本、最直观的表达形式；频域特征是对信号的频率变化和分布情况进行分析得出的与频率相关的特征，包括重心频率、均方频率等；时频域特征则提供了时间域与频率域的联合分布信息，描述了信号频率随时间变化的关系，主要有短时傅里叶变换、小波变换、Wigner-Ville 变换、希尔伯特-黄变换等。

小波包分解采用小波变换，对信号进行逐层分解形成一个完整的树状结构，它可以根据需要调整时间与频率分辨率，而对信号本身的信息造成的损失比较小，具有多分辨分析的特点。

本文采用中国科学院声学研究所的InSAS 2008 型电容式次声传感器分别在海南、西昌、白城等地搭建了实验台站，设置STA/LTA 事件检测算法的长时窗为50 s，短时窗为5 s，检测阈值为3.2，收集了大量的事件信号(包括闪电、台风、化爆试验等)。通过对这些信号进行分析，从中选取了108 个信号，组成实验信号样本。然后又从台站采集的数据中提取出507 段信号(这些信号实为噪声)，与上述事件信号共同组成机器学习的样本库。

某次事件信号的时域波形和频域波形如图2所示，对信号进行3层小波包分解，每个节点的分解系数如图3所示。

利用小波包分解系数对信号进行重构，得到各频带内的重构信号如图4所示，计算各频带内重构信号的能量占总能量的百分比如图5所示。

对所有采集的信号进行小波包分解，然后利用小波包分解系数对信号进行重构，计算各频带内重构信号的能量占总能量的百分比。可以发现这些事件信号的频率主要集中在15 Hz 以下，在25～50 Hz频段范围内的信号能量基本为0，因此只能选取小波包分解前半部分节点的能量占比作为特征向量，则需要对这些信号数据进行k(k= 2，3，···，6)层小波包分解，构造出的特征向量V的维数等于n(n=2k-1，k=2，3，···，6)，计算方法如下：

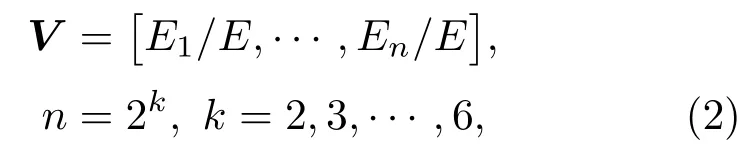
式(2)中，E表示信号总能量；E1～En表示各频带内的能量。

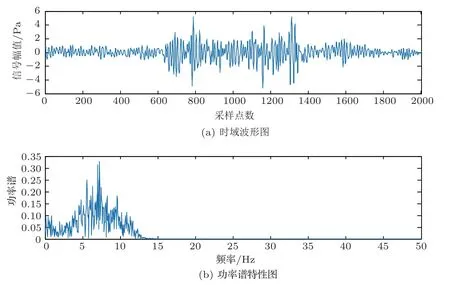
图2 信号时域波形和频域波形Fig.2 Time-domain waveform and frequency-domain waveform

图3 小波包分解第3 层系数图Fig.3 Layer 3 coefficient diagram

图4 小波包分解第3 层系数重构信号Fig.4 Reconstructing signal with Layer3 coefficient

图5 小波包分解各频段能量占比Fig.5 Energy proportion of each frequency band

3 基于SVM的次声事件识别

3.1 SVM理论

SVM是AT＆T Bell实验室的Vapnik博士等基于统计学学习理论提出的一种机器学习方法，它根据结构风险最小化准则，在使训练样本分类误差最小化的前提下，尽量提高分类器的泛化推广能力[7-10]。

3.1.1 基本思想

当样本线性可分时，需要找到一个超平面将不同类的样本分开，而其中的最优超平面则是能使得离超平面较近的异类点之间有更大的间隔，即不必考虑所有样本点，只需让求得的超平面使得离它近的点间隔最大。简化到二维的情况，如图6所示。

在样本空间中，划分超平面可通过式(3)所示的线性方程来描述：

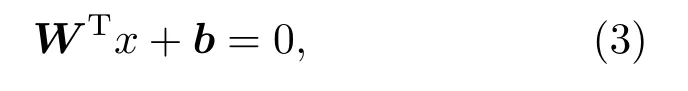
其中，W为法向量，决定了超平面的方向；b为位移量，决定了超平面与原点的距离。对于训练样本(xi，yi)，满足以下公式：

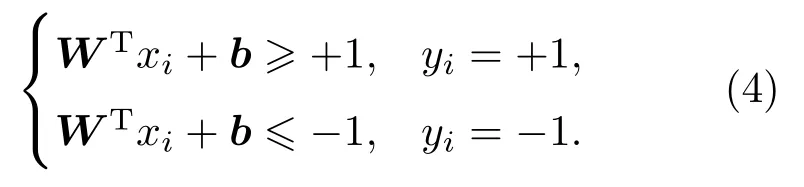
距离超平面最近的这几个样本点满足yi(WTxi+b)=1，它们被称为“支持向量”。虚线称为边界，两条虚线间的距离称为间隔，用γ表示：

通过求取||W||的最小值，可以得到最优分类超平面。

图6 SVM 的原理示意图Fig.6 Diagrammatic sketch of SVM

3.1.2 核函数

对于非线性问题，上述方法并不能有效解决。这种情况下，SVM采用的方法是将训练样本从原始空间映射到一个更高维的空间，使得样本在这个空间中线性可分，如果原始空间维数是有限的，即属性是有限的，那么一定存在一个高维特征空间使样本可分。令φ(x)表示将x映射后的特征向量，于是在特征空间中，划分超平面所对应的模型可表示为

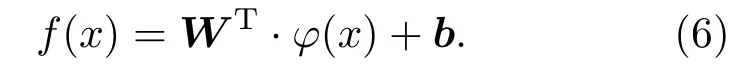
求||W||的最小值可以转化为其对偶问题的求解，需要计算φ(xi)T·φ(xj)。由于特征空间的维数可能很高，甚至是无穷维，因此直接计算φ(xi)T·φ(xj)通常是困难的，于是引入一个函数：

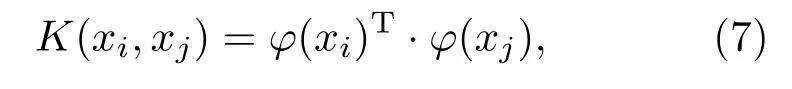
即在原始样本空间中通过函数K(xi，xj)来计算φ(xi)T·φ(xj)的值，省去高维计算的复杂情况。

3.1.3 松弛变量

当训练样本中有少量样本点落在超平面与边界之间时，为了防止过拟合，可以对每个样本点引入一个松弛变量ξi≥0，使得间隔加上松弛变量大于等于1，来近似为线性可分，约束条件变为

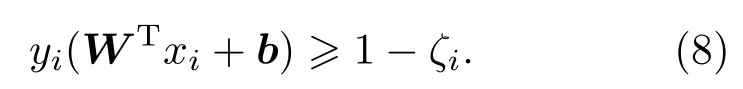
同时，对于每一个松弛变量，支付一个代价C，目标函数变为

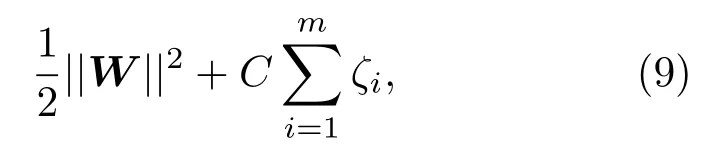
其中，C ＞0 为惩罚参数，C值大时对误分类的惩罚增大，C值小时对误分类的惩罚减小。要使式(9)取最小值，则需要间隔尽量大，同时使误分类点的个数尽量少，C是调和两者的系数。然后，就可以采用与线性可分SVM一样的方法进行学习。

3.2 次声事件识别

通过对采集的次声数据进行分析，从中提取出507 个噪声数据，加入采集的108 个事件数据，进行基于SVM的次声事件识别实验。实验中，分别从噪声数据和事件数据中随机抽取4/5的样本作为训练集，对SVM进行训练，其余样本作为测试集，以检验训练得到的SVM 的分类能力。为了消除训练集和测试集随机选取带来的影响，实验进行多次运行，然后对结果进行统计。

当进行两层小波包分解时，得到4 个频带的能量(E1、E2、E3、E4)，由于高频段的E3和E4趋于0，所以选取特征向量V= (E1/E，E2/E)，特征向量的维数等于2，此时分类效果比较差，在最好的情况下正确率只有0.782258，如图7所示。

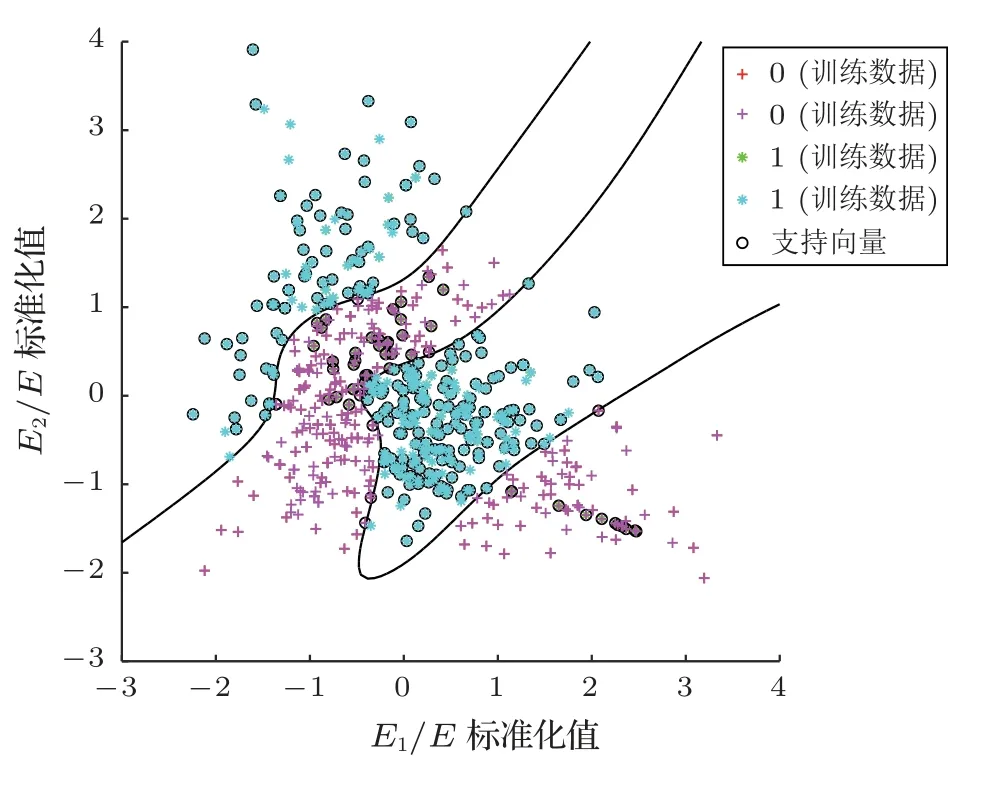
图7 二维特征向量的分类结果Fig.7 Classification results of two-dimensional eigenvectors

选取不同的特征向量维数，分别采用不同的核函数对模型进行训练，并进行测试，实验结果见表1。

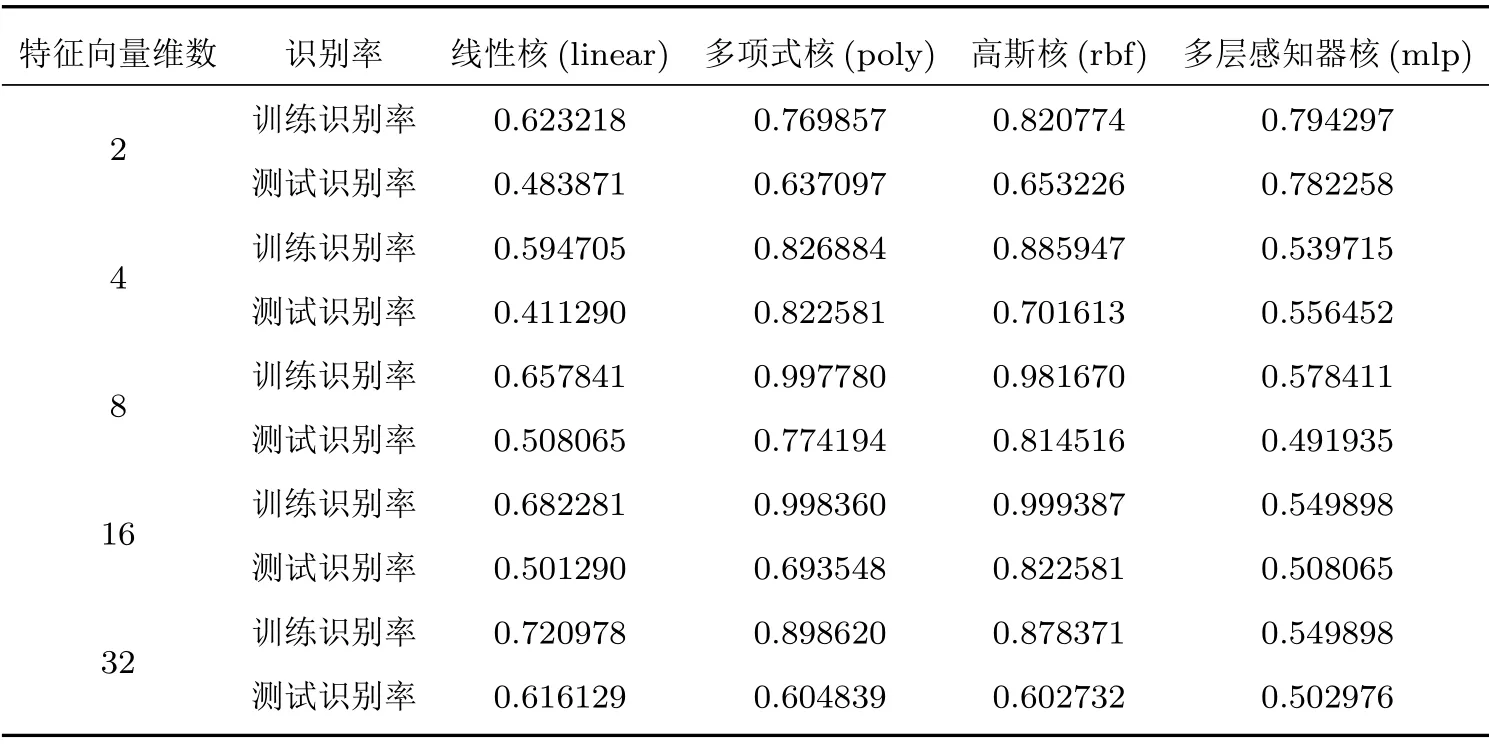
表1 不同核函数的识别率Table1 Recognition rate of different kernel functions

3.3 结果分析

假设n是特征向量维数，m是训练数据集的样例个数，根据实验结果可知，当n比较小(如n= 2、4)、m比较大(如m= 492)时，m/n ＞100，那么一般需要增加特征，提高特征向量的维数，并且使用多项式核函数的SVM 算法，来对识别性能进行改善；如果n相对于m大小适中(如n= 8、16)，20＜m/n ＜100，可以使用高斯核函数的SVM 算法；如果n相对m来说比较大，m/n ＜20，各种核函数的分类效果相差不大，但线性核函数参数少、速度快，可以得到较高的运算性能。

SVM 性能的优劣与特征向量的维数和核函数的选取有很大关系，所以对于一个实际问题而言，需要对不同的特征进行组合，在不同的特征空间中进行分类识别，并选择合适的核函数来构造SVM 算法。目前比较成熟的核函数及其参数的选择都是实验人员根据自己的经验来选取的，带有一定的随意性。而针对不同的问题，核函数应当具有不同的形式，所以在选取时候应该充分研究信号特征的物理意义，从而选取更加适合的核函数。

4 基于ANN的次声事件识别

4.1 ANN模型

ANN 是模拟人脑对信息的处理方法而建立的一种运算模型。它由输入节点、隐含节点、输出节点(相当于人脑神经元)相互联接构成，对每个节点的输入数据采用激励函数进行运算，输出运算结果。两个不同层节点之间的连接对应于一个通过该连接信号的权值，相当于ANN 的记忆。网络的输出则根据网络的连接方式、权值和激励函数的不同而不同[11-13]。典型的单隐层ANN结构如图8所示。

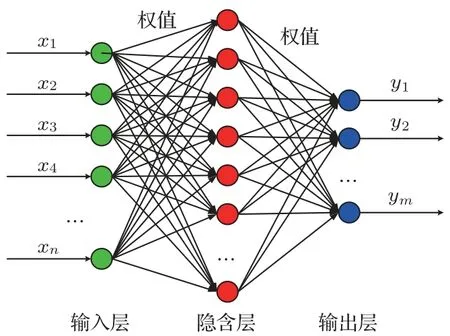
图8 ANN 结构图Fig.8 Structure diagram of ANN

4.2 次声事件识别

实验仍然采用上述数据集，神经网络选用3 层结构的前馈网络模型，其输入层的节点个数和特征向量的维数一致(8 个节点)，输出层为一个节点，输出结果为0 (表示输入为噪声数据)或1(表示输入为事件数据)。采用tansig 函数作为激励函数，输出节点为线性函数。在确定了输入层和输出层个数以及激励函数后，还需要确定其隐含层的节点个数，本文采用经验公式(10)来初步确定隐含层节点数的大概范围。

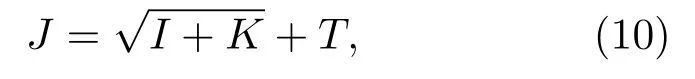
其中，J为隐含层节点个数，I和K分别为输入和输出层节点数，T为1～10 之间的常数。据此，选取隐含层神经元个数为4(T= 1)、5(T= 2)、7(T= 4)、9(T=6)、11(T=8)、13(T=10)个，建立神经网络分别进行实验，实验中训练集和测试集分组方法和SVM 实验相同，并对多次运行的结果进行统计，来消除训练集和测试集随机选取带来的影响，实验结果如表2所示。

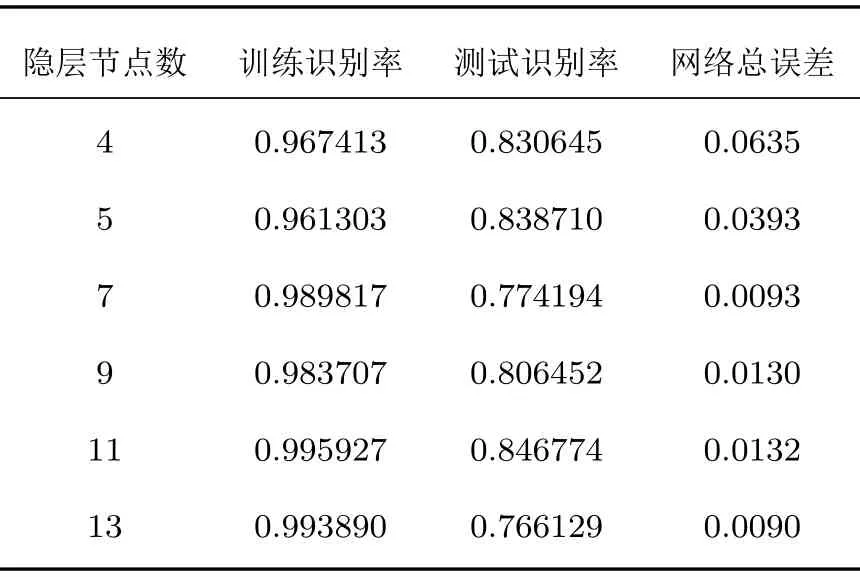
表2 不同隐层节点数的识别率Table2 Recognition rate of different hidden nodes

隐层节点数为11时，误差随迭代次数的变化曲线如图9所示，可以看出误差收敛的速度比较快。

图9 误差随迭代次数的变化曲线Fig.9 Error of iterations

4.3 结果分析

隐层节点数过少时，会导致生成的网络欠拟合，训练识别率和测试识别率都比较低，网络性能达不到预期效果；隐层节点数过多时，网络计算量增大，并容易产生过拟合问题，从而导致网络性能也下降。除此之外，随着节点数的增多，网络收敛的速度会相应的有所增加，网络总误差会有所减小，但误差的大小除了取决于节点数外，还和结束迭代的目标误差有关，所以总误差只能作为评价网络性能的参考值。

5 结论

SVM 是一种针对有限样本情况的机器学习方法，其目标是根据现有样本数据得出最优解，而不是在样本数趋于无穷大时的最优解。从实验中可以看出，当样本数量不够多时，SVM 的识别能力要优于ANN，符合理论分析。因此，可以结合SVM和ANN的特点，在样本数量比较小的情况下，采用SVM 的识别模型来对事件进行识别，并研究寻找更为有效的核函数，提高识别性能；当样本数量达到一定规模时，采用ANN 的方法进行学习，发挥ANN 深度学习的优势。

在实际工程应用中，可以适当降低事件检测算法的检测阈值，提高检测率(虽然同时误报率也升高)，然后提取次声信号的特征向量，经过机器学习对信号进一步识别判断，从而提高总的事件识别率，最后采用互相关算法计算其时间延迟并进行定位。