阵风场中桥上列车升力气动导纳数值模拟及应用研究

2020-06-08段青松吴再新李建兴马存明

铁道科学与工程学报 2020年5期

段青松，吴再新，李建兴，马存明

段青松1，吴再新1，李建兴1，马存明2

(1. 四川省铁路产业投资集团有限责任公司，四川成都 610041；2. 西南交通大学土木工程学院，四川成都 610041)

针对阵风场中列车中车二维升力气动导纳展开研究。基于数值模拟的方法，首先验证平板升力气动导纳模拟结果的可靠性，其次对单独列车截面的升力气动导纳及绕流特性进行分析，并与桁架梁、流线型钢箱梁上列车升力气动导纳进行对比。研究结果表明：平板升力气动导纳数值结果与解析解吻合较好，数值识别方法可靠。桥梁主梁上列车升力气动导纳比单独列车升力的气动导纳值偏小，比Sears函数略偏大；当折减频率小于0.01时，流线型钢箱梁上列车升力气动导纳略大于桁架梁上列车气动导纳值。

阵风；列车；升力；气动导纳；数值模拟

为了促进我国西部地区经济发展，满足人民日益增长的交通需求，建设大跨度铁路桥梁是必然选择。目前已建或在建的铁路桥梁主梁大多为钢桁梁，如沪通长江大桥、平潭海峡公铁两用大桥、铜陵长江公铁大桥和公安长江公铁大桥。相比钢桁梁，流线型钢箱梁结构轻盈、造型美观、稳定性好，公铁平层的超宽流线型钢箱梁更是首创。横风中列车的气动力特性，不仅与其自身的气动外形有关，而且受基础设施(如：桥梁，路堤)的影响。车辆改变了桥梁主梁的气动绕流结构，而桥梁主梁的几何外形也会对桥上高速列车的气动荷载产生影响[1−2]。车辆与桥梁主梁间存在着相互气动作用，单独进行车辆或桥梁主梁气动参数的研究都将导致较大的误差。国内外多名学者对此展开了针对性研究。Cooper[3]通过风洞试验测压法研究了地面上移动列车的气动导纳函数，结果与Vickery和Bearmen提出的矩形平板气动导纳的公式吻合较好。考虑风偏角影响，Baker等[4−6]通过现场实测得到了列车的气动导纳。Baker[7]通过现场实测和风洞试验给出了不同风偏角下列车的气动导纳函数，认为列车气动导纳应考虑二维准定常效应。Cheli等[8]通过风洞试验分析了紊流风对平板上列车受到的定常、非定常的气动力影响，研究了雷诺数对列车表面压力分布的影响，得到列车气动导纳函数。Sterling等[9]对不同类型列车的气动导纳函数进行了总结。Tomasini等[10]通过风洞试验验证了列车气动导纳数学模型的合理性，但由于漩涡脱落的影响，数值模型不适合于列车升力导纳。MA等[2]研究了钢桁架主梁上列车压力分布特性、抖振力展向相关性及气动导纳函数，分析了列车位置、紊流场、攻角等因素的影响。总之，上述研究多针对列车运行于路堤或桥梁的工况，不同桥梁断面对列车气动导纳影响的分析较少，有必要对不同断面主梁上列车气动导纳进行对比研究，以进一步深入总结归纳列车气动导纳函数的变化规律，为风车桥耦合计算分析提供基础。列车截面属钝体，其周围的流场复杂，无法通过常规的风洞试验对其周围的流场分布特性展开研究，CFD数值模拟技术不仅可以方便探测列车周围的流场分布特性，而且可以有效分析其平均气动力特性及气动导纳函数。同时，数值模拟可以直接生成完全单一频率的谐波风场，提取气动力简单便捷，费用低[11]，有很大的优势。Uejima 等[12]基于二维雷诺平均的方法研究了平板、长宽比5:1矩形断面及扁平六边形断面的气动导纳，平板气动导纳模拟结果与Sears函数十分接近，矩形断面与扁平六边形断面的气动导纳与试验结果十分接近。韩艳等[13]推导了6个复气动导纳定义式，基于三维的雷诺平均方法研究了平板的气动导纳，所得结果与Sears函数存在一定的差别，且最大折算频率不超过0.6。Hejlesen等[14]通过无网格涡的方法计算了桥梁断面的气动导纳。钝体断面气动导纳的数值识别方法尚属起步阶段，高速铁路列车中车断面可以认为是带圆弧倒角的1:1的矩形断面，基于雷诺平均的CFD数值模拟方法识别此类断面气动导纳的研究鲜有报道，本文对钢桁架梁及公铁平层的流线型钢箱梁上列车气动升力气动导纳函数展开研究。

1 数值模拟方法

1.1 基本控制方程

数值模拟时采用的计算方法如下：时间离散采用二阶隐式，对流项为二阶迎风格式，其他流动物理量的空间离散也采用二阶格式，基于SIMPLEC算法处理压强与速度耦合，湍流模型采用模型，连续性方程的收敛值设置为1×10−6；采用FLUENT软件完成计算，基本控制方程不赘述。

1.2 计算区域与边界条件

模型的计算区域如图1所示，为截面宽，计算域长度为18，宽度为6，模型位于距离速度入口6位置处。在计算域左侧边界为速度入口条件，方向速度保持恒定不变，方向速度随时间简谐变化，通过用户自定义函数(UDF)编程实现，上下边界为无滑移的Wall边界条件，右侧边界为自由出流边界条件，结构表面为无滑移的Wall边界条件。

图1 计算区域示意图(B为截面宽)

唐煜等[11]通过数值验证得出：非均匀初始化技术可以节约来流边界时变信息传播到数值计算关心区域的时间1，对于结构断面存在所造成的有物理意义的流场收敛需要时间2，当时间1并非远大于时间2时，非均匀初始化并无明显优势。Uejima等[12]在进行数值计算时，设置上、下边界条件为Wall边界条件，且流场初始化与计算精度无关，只涉及计算效率。本文设置上、下边界条件为Wall。

在数值模拟时，随时空变化的计算入流边界条件必须满足在无障碍物的整个计算域中保持其边界特征，即入流自保持能力。为保证来流脉动速度的自保持，根据计算分析[11]，首先，计算域网格最大尺寸Δ应满足/，为待识别断面的宽度，单波长内网格数，为折减频率，且不应小于80；其次，无量纲时间步长d/Δ小于1.2，d为时间步长。

1.3 气动导纳识别方法

升力气动导纳计算可参考式(1)：

本文中数值模拟采用二维计算方法，即：列车模型为展向无限长；来流紊流为单一频率的简谐波，认为来流紊流为展向完全相关的。因此，数值模拟得到的气动导纳为二维气动导纳。

1.4 平板升力气动导纳验证

对于理想平板的升力气动导纳的Sears函数，Liepmann给出了近似解：

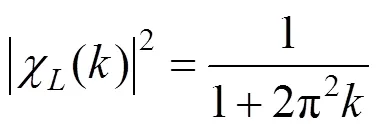
计算时取宽高比为100:1的矩形平板，宽为1 m，高为0.01 m，平板的阻力系数为0，升力系数斜率为2π。网格划分时，保持外围为均匀化结构网格，结构断面周围为非均匀化网格且适当加密。通过尺寸函数(size function)控制网格尺寸从壁面到均匀网格的渐变，相邻网格尺寸增长因子为1.03，保证+值小于5，网格总数约为2.5×105。来流边界条件为：水平向为均匀流，风速取为10 m/s；竖向为单频率的简谐波，幅值为0.336 m/s，湍流强度取为2%，即简谐脉动速度为单向。

关于纵向来流风速对气动导纳的影响，许多学者做过针对性研究。马存明[15]认为，风速对气动导纳的影响较小，靳欣华[16]也认为，在气动导纳随风速的变化趋势不明显，原因是不同风速下的紊流强度和紊流积分尺度基本一致，而这是影响气动导纳的重要因素。本文中数值模拟在低风速下进行，故文中所列结果仅适用于低雷诺数的情况。

为了检测时间步长对计算结果的影响，图2给出了无量纲折减频率为0.416 67时，时间步长为0.000 5，0.001，0.002和0.005 s时的气动导纳结果。随着时间步长的增大，CFD数值模拟的气动导纳结果与解析解偏离逐渐增大，其中当时间步长为0.000 5 s时，CFD结果与解析解偏离约8%，当时间步长为0.001 s时，偏离约15%。鉴于普通计算机的计算能力，可在满足计算结果要求的前提下适当增大时间步长。图3给出了宽高比为100的平板升力气动导纳的识别结果，并与Sears函数对比。从图3可知，在高折减频率与低折减频率时，平板气动导纳的数值识别结果与根据势流理论推导的Sears函数吻合较好，认为该数值识别方法可靠。

图2 时间步长对数值模拟结果影响(k=0.4167)

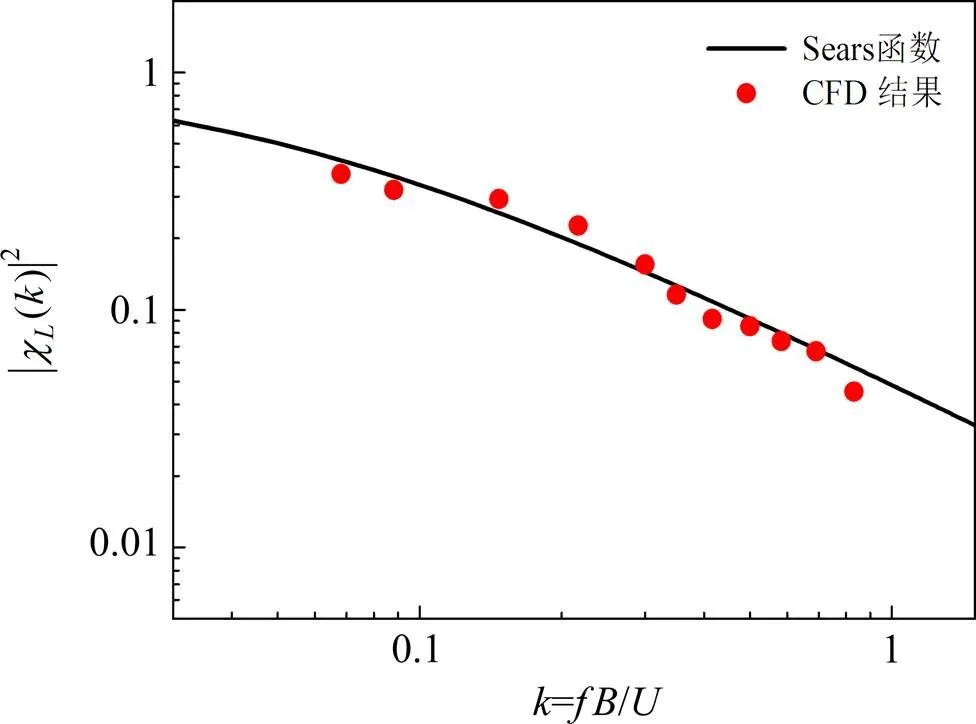
图3 平板气动导纳数值识别结果

2 单独列车升力气动导纳

1列高速列车通常由很多节车厢组成，中部车厢形状不变，故一般按头车、中车和尾车分类，本文主要针对列车的中车进行研究，列车模型底部忽略了转向架等的影响并简化为平面，且未考虑受电弓等构件，列车截面如图4所示。计算区域及列车周围的网格划分见图5。在列车周围的网格加密，通过尺寸函数控制网格尺寸从壁面到均匀网格的渐变，相邻网格尺寸增长因子为1.03；在远离列车模型区域，采用稀疏的网格，+值小于5，网格总数约为3×105。

单位：m

图6给出了静止列车的气动导纳数值模拟结果，并与平板的升力气动导纳——Sears函数对比。结果表明，列车升力气动导纳比Sears函数偏大，但变化趋势基本一致。在折减频率小于0.05时，气动导纳数值接近于1，随着折减频率的增大，气动导纳逐渐减小。需要说明的是，数值模拟时无量纲频率只到10−2次方左右，这主要与计算量及计算时间有关。列车中车截面与带倒角的1:1矩形截面类似，对单独的列车中车进行数值模拟的目的是分析列车中车截面自身的气动特性，为后续探讨基础设施(桥梁、路堤)气动影响奠定基础。

图5 网格划分

图6 静止列车升力气动导纳数值识别结果

Jancauskas[17]在均匀正弦紊流场中测得了机翼以及不同宽高比的矩形断面的气动导纳结果(见图7，图中坐标均为线性坐标)，其结果表明，测得的机翼断面的气动导纳与其理论值吻合较好；随着矩形断面宽高比的增大，其气动导纳值逐渐接近于Sears函数，随着矩形断面宽高比的减小，其值在低频范围内接近于1。其认为主要原因是机翼断面的升力完全由附着流产生；钝体断面的升力不仅由附着流产生，而且有分离流的作用；随着矩形断面宽高比的减小，分离流的作用产生升力的比例增大。

3 桥梁上列车升力气动导纳数值模拟初探

对2种主梁断面进行分析，分别为钢桁梁和流线型钢箱梁。钢桁架主梁断面如图8所示，主梁宽22.0 m，高12.0 m；流线型钢箱梁断面如图9所示，主梁截面宽63.9 m，高5.0 m，左右车道为公路，中间I~IV车道为铁路。为了准确分析列车受到的气动力，列车与桥梁之间不允许有任何接触。

单位：m

图10给出了桥上列车周围网格。在主梁及列车周围的网格加密，通过尺寸函数控制网格尺寸从壁面到均匀网格的渐变，相邻网格尺寸增长因子为1.03；在远离主梁及列车模型区域，采用稀疏的网格，y+值小于5，网格总数约为5×105数值模拟计算方法及边界条件等与第1节一致。

单位：m

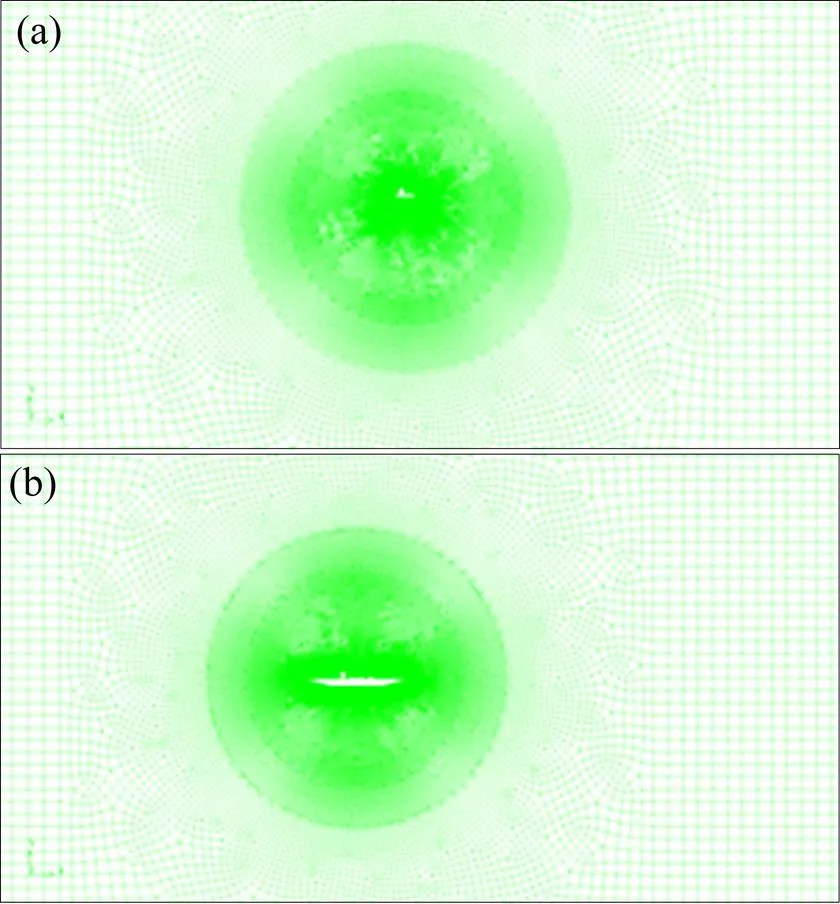
(a) 桁架梁上列车周围网格；(b) 流线型钢箱梁上列车周围网格

图11 列车升力气动导纳(0°攻角)

图11给出了钢桁架梁与流线型钢箱梁上迎风侧列车的气动导纳数值模拟结果，并与Sears函数对比。结果表明，桥梁主梁上列车升力气动导纳比单独列车升力的气动导纳值偏小，比Sears函数略偏大，随折减频率的增大而逐渐减小。这也说明不考虑桥梁主梁的影响，单独进行列车气动导纳分析是不可靠的。同时，在折减频率小于0.01时，流线型钢箱梁上列车升力气动导纳略大于桁架梁上列车气动导纳值。

4 二维气动导纳应用机理

上节中，对桥梁上列车二维气动导纳进行了数值模拟研究，本部分就其应用展开研究，具体如下。

对于有限展长的节段，两波数的升力系数谱[18]为：

对两波数谱在展向积分，可以得到一波数谱：

同时，一波数升力系数谱又可以由来流紊流风谱写成如下形式：

则：

式(7)代入式(6)，可得三维气动导纳函数为：

式(8)中的两波数气动导纳函数被一波数气动导纳函数代替，则有二维气动导纳函数：

为了评价三维气动导纳与二维“片条理论”分析的差异性，式(8)与式(9)的比值可以表示为：

当节段展长趋近于无穷时，式(10)可简化为：

当节段趋近于有限展长的“片条”时，式(10)可简化为：

由式(11)可知，当模型沿展向无限长时，三维气动导纳与二维气动导纳函数相等，即：对于无限展长的模型，其气动导纳函数为二维的。由式(12)可知，对于“片条”，其气动导纳函数不考虑展长相关因子的影响，其比值与节段的长度也就无任何关系。对比式(11)与式(12)可知，结构的长宽比(展长/截面宽度)达到一定程度时，节段的三维气动导纳函数与二维气动导纳函数就可以认为基本一致。

对于多个编组的列车而言，其长度远大于宽度，为细长结构，可以将二维气动导纳运用于风车桥耦合计算中，这也是研究结构二维气动导纳函数的意义。

5 结论

1) 平板气动导纳的数值识别结果与Sears函数吻合均相对较好，验证了该识别方法的可靠性。探讨时间步长对识别结果的影响，在满足计算结果要求的前提下适当增大时间步长。单独列车的升力气动导纳比Sears函数偏大，但变化趋势基本一致；折减频率小于0.05时，气动导纳数值接近于1，随着折减频率的增大，气动导纳逐渐减小。

2) 初步探索识别了桥梁主梁上列车升力气动导纳。桥梁主梁上列车升力气动导纳比单独列车升力的气动导纳值偏小，比Sears函数略偏大，随折减频率的增大而逐渐减小。折减频率小于0.01时，流线型钢箱梁上列车升力气动导纳略大于桁架梁上列车气动导纳值。一个编组列车的长度远大于宽度，可将列车二维气动导纳应用于风车桥耦合计算分析。

[1] 郭文华, 张佳文, 项超群. 桥梁对高速列车气动特性影响的风洞试验研究[J]. 中南大学学报(自然科学版), 2015, 46(8): 3151−3159. GUO Wenhua, ZHANG Jiawen, XIANG Chaoqun. Wind tunnel test of aerodynamic characteristics of high-speed train on bridge[J]. Journal of Central South University (Science and Technology), 2015, 46(8): 3151−3159.

[2] MA Cunming, DUAN Qingsong, LI Qiusheng, et al. Buffeting forces on static trains on a truss girder in turbulent crosswinds[J]. Journal of Bridge Engineering. 2018, 23(11): 1−19.

[3] Cooper R K. The effect of cross-winds on trains[J]. Journal of Fluids Engineering, 1981, 103(1): 170−178.

[4] Baker C J. Ground vehicles in high cross winds Part I: Steady aerodynamic forces[J]. Journal of Fluids & Structures, 1991, 5(1): 69−90.

[5] Baker C J. Ground vehicles in high cross winds Part II: unsteady aerodynamic forces[J]. Journal of Fluids & Structures, 1991, 5(1): 91–111.

[6] Baker C J. Measurements of the cross wind forces on trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7): 547−563.

[7] Baker C. The simulation of unsteady aerodynamic cross wind forces on trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 98(2): 88−99.

[8] Cheli F, Giappino S, Rosa L, et al. Experimental study on the aerodynamic forces on railway vehicles in presence of turbulence[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123(6): 313−316.

[9] Sterling M, Baker C, Bouferrouk A, et al. An investigation of the aerodynamic admittances and aerodynamic weighting functions of trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(11): 512−522.

[10] Tomasini G, Cheli F. Admittance function to evaluate aerodynamic loads on vehicles: experimental data and numerical model[J]. Journal of Fluids and Structures, 2013, 38(3): 92−106.

[11] 唐煜, 郑史雄, 张龙奇, 等. 桥梁断面气动导纳的数值识别方法研究[J]. 空气动力学报, 2015, 33(5): 706−713. TANG Yu, ZHENG Shixiong, ZHANG Longqi, et al. Numerical method for identifying the aerodynamic admittance of bridge deck[J]. Acta Aerodynamic Sinica, 2015, 33(5): 706−713.

[12] Uejima H, Kuroda S, Kobayashi H. Estimation of aerodynamic admittance by numerical simulation[C]// BBAA VI International Colloquium on Bluff Bodies Aerodynamics and Applications, Milano, Italy, 2008: 20−24.

[13] 韩艳, 陈政清. 薄平板复气动导纳函数的试验与数值模拟研究[J]. 振动工程学报, 2009, 22(2): 202−206. HAN Yan, CHEN Zhengqing. Experimental and numerical simulation studies on complex aerodynamic admittance functions of thin plate section[J]. Journal of Vibration Engineering, 2009, 22(2): 202−206.

[14] Hejlesen M M, Rasmussen J T, Larsen A. On estimating the aerodynamic admittance of bridge sections by a mesh-free vortex method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 146(11): 117−127.

[15] 马存明. 流线箱型桥梁断面三维气动导纳研究[D]. 成都: 西南交通大学, 2007. MA Cunming. 3D aerodynamic admittance response of streamlined box bridge decks[D]. Chengdu: Southwest Jiaotong University, 2007.

[16] 靳欣华. 桥梁断面气动导纳识别理论及试验研究[D]. 上海: 同济大学, 2003. JIN Xinhua. Identification of aerodynamic admittance of bridge decks: Theory and experiment[D]. Shanghai: Tongji University, 2003.

[17] Jancankas E D. The aerodynamic admittance of 2-D rectangular section cylinders in smooth flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 23: 395−408.

[18] Hakkinen R J, Richardson A S. Theoretical and experimental investigation of random gusts loads[J]. Technical Report Archive & Image Library, 1957(3878).

Numerical simulation and application investigation on lift aerodynamic admittance of railway vehicles on bridge girders in gust

DUAN Qingsong1, WU Zaixin1, LI Jianxing1, MA Cunming2

(1. Sichuan Railway Investment Group Company Limited, Chengdu 610041, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610041, China)

Two-dimensional lift aerodynamic admittance function (AAF) of railway vehicles in gust was investigated. Based on the numerical simulation method, the reliability of lift AAF of a thin plate was tested. Then, the AAF and flow characteristics of a single middle railway vehicle were investigated. The AAF results of railway vehicle on truss girder and streamlined steel box were also compared with that of a single railway vehicle. The results show that the numerical simulation results of the thin plate are consist with the theoretical solution, which is of reliability. The lift force AAF values of vehicle on girders are a little smaller than that of a single vehicle, and larger than that of the Sears function. When the non-dimensional frequency is smaller 0.01, the lift force AAF values of railway vehicles on streamlined box girder are larger than that of railway vehicles on truss girder.

gust; railway vehicle; lift; aerodynamic admittance; numerical simulation