求解三维边坡安全系数的最小势能法研究

2020-06-08孙加平魏星詹凤程

铁道科学与工程学报 2020年5期

孙加平，魏星，詹凤程

求解三维边坡安全系数的最小势能法研究

孙加平，魏星，詹凤程

(江西工业工程职业技术学院能源工程学院，江西萍乡 337055)

为有效评价岩土体的稳定性，运用最小势能法进行三维边坡的稳定性分析。通过引入土弹簧模型、依据滑体整体静力平衡方程，计算滑体系统的弹性压缩势能以及剪切势能。基于物体在自重作用下沿斜面运动规律，确定微面下滑方向，将整个滑体的潜在运动方向视为微面滑动方向的矢量和。将边坡的安全系数定义为沿着滑动方向得到的抗滑力与下滑力的比值。为验证文中计算方法的合理性，计算了一个经典算例的安全系数。研究结果表明：文中计算方法得到的解答与其他算法的相对误差在10%范围内，表明文中计算方法可用于三维边坡的稳定性分析；随着土体抗剪强度指标的增大，边坡的安全系数呈现线性增大的趋势；当三维滑体的横向尺寸与纵向尺寸之比大于5时，可以将三维边坡的稳定性分析视为平面应变问题处理。

边坡；稳定性；最小势能法；下滑方向；安全系数

最小势能法作为边坡稳定性分析的一种方式，该方法依据系统势能最小时，系统处于稳定平衡状态，通过求解使得系统势能处于最小状态下的虚位移，最后通过力与虚位移之间的关系进行安全系数的计算[1−2]。总体而言，该方法具有无需划分条块、安全系数无需迭代等优点，逐步被一些学者重视[3−4]。目前，基于最小势能原理的二维边坡稳定性分析方法的研究已经趋于成熟[5−6]。因此，运用最小势能法进行三维边坡稳定性的分析有助于该理论体系的完善[7]。将最小势能法从二维扩展至三维，主要有以下2个问题需要解决：其一，系统势能由弹性压缩势能、剪切势能以及外力势能组成，弹性势能以及外力势能容易获得，而计算剪切势能的焦点在于如何获得滑面上的剪应力；其二，一般而言，坡体的潜在滑动方向沿着滑裂面的切向。对于二维边坡的分析，滑面上的一点的切向是确定的。然而，对于三维滑面，过滑面上任意一点的切向不具有唯一性。因此，如何确定三维滑体的运动方向是边坡稳定性分析的亟需解决的问题。针对上述问题，温树杰等[7−8]进行了初步的研究，通过取微单元体为研究对象，假设主滑面进行滑面上剪应力的计算。同时，将坡体的潜在滑动方向视为使得系统势能最小的虚位移方向。虽然得到了一些有益的结论，但对于滑面上剪应力的计算过程较为复杂，且将潜在滑动方向视为虚位移方向值得商榷。因此，针对上述2个主要问题，本文在作者已有研究成果[9]的基础上，将二维边坡稳定性分析方法扩展至三维。通过滑体整体沿着虚位移方向的静力平衡方程确定滑面上的剪应力，以此确定滑体系统储存的剪切势能。同时，依据运动学的观点确定滑体微单元的潜在滑动方向，将滑体整体运动方向视为微单元滑动方向的矢量和。最后，把作用于滑体上的力沿着滑动方向投影分别得到抗滑力与下滑力，将二者的比值作为边坡的安全系数。为了验证本文计算方法的合理性，运用本文方法计算了一个经典边坡算例的安全系数，并将得到的安全系数与其余算法进行对比。同时，探究土体的抗剪强度指标、滑裂面形状对边坡安全系数的影响规律。

1 稳定性分析模型

1.1 构建势能函数

图1 边坡示意图

根据假定(2)可得微面d法向由于弹性压缩变形产生的法向力大小

式中：x为微面法向产生的弹性压缩变形量，m。

则系统的弹性压缩势能U为

为了计算系统的剪切势能，从图1中滑床上取高度为h微元体进行分析，如图2所示。

系统的剪切势能为

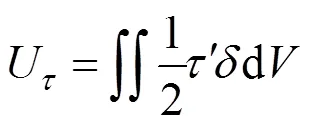
式中：′为在合外力作用下微面d上的剪应力，kPa；为与′对应的剪应变，rad；d微元体体积，且d=d，m3。

显然，为了求解剪切势能必须确定′和，通过图2可得

式中：′为微面d上的剪切位移，m；为微面d上的抗滑剪力单位向量，且=(1,2,3)。

因此，能否正确进行的计算，关键在于′。孙加平等[8]通过取图1中的单元体为研究对象，基于单元体的静力平衡关系求解，然而在建立平衡方程时忽略了单元体的条间力的影响。通过上文所述可知，滑体发生一个虚位移，滑体处于稳定平衡状态，则滑体中任取的单元体亦平衡。由于局部处处平衡，故而整体必定平衡。因此，可以通过滑体整体沿着虚位移方向的静力平衡关系，确定微面d上的剪应力。通过分析可知，滑体在合外力、剪切力以及法向力作用下保持平衡，即

则微面上的剪应力为

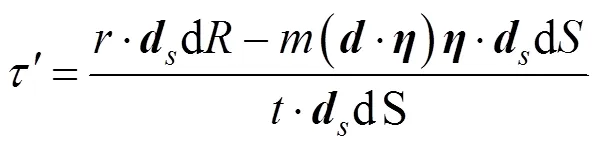
式中：d为作用于微面上的合外力，kN。

将式(5)变形可得

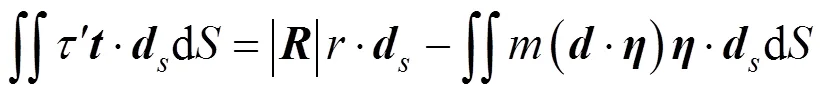
由式(3)，(4)和(6)得

则系统总势能为

则在给定的外力条件下，总势能对虚位移的一阶偏导需满足

式(10)是一个线性方程组，虚位移易求得，则根据力与位移的关系，可求解微面d上的法向应力，即

1.2 确定微面抗滑方向t

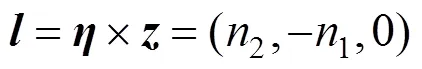
解方程组(13)可得

1.3 确定三维边坡的安全系数

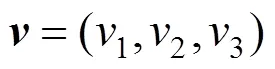
式中：为土体的黏聚力，kPa；为土体的内摩擦角，rad。

通过分析可知，滑体上的合外力提供下滑力，滑面上的法向力、剪切力提供抗滑力，则安全系数s为

2 算例验证分析

众多学者为了验证三维边坡稳定性分析方法的合理性，均采用文献[12]中的经典算例。算例具体信息如下：潜在滑裂面为旋转椭球面，即

其中：，，且该椭球滑体在xoz平面上的投影如图3所示，已知：土体的容重γ=18.8 kN/m3，黏聚力c=29 kPa，内摩擦角φ=20°，坡高为12.2 m，B(10,0)。

由于研究表明[7−8,13]，对于均质边坡安全系数的计算结果与无关，因此算例中并未给出具体数值。经计算可得滑体体积为1.209 8×104m3，滑面提供的抗滑力大小为3.762 6×105kN，下滑力大小为1.753 27×105kN，则运用本文方法得到的安全系数为s=2.146，其他方法得到的结果见表1。

表1 不同方法计算的安全系数

从表1可以看出文中的计算方法与已有研究给出的解答较为接近，相对误差在10%范围内，满足工程上的精度要求，表明文中计算方法具有一定的合理性。此外，文中计算方法相比于文献[11]、文献[8]安全系数要小，工程应用偏安全。并且，文中关于剪应力、滑体下滑趋势的计算模型，相比于文献[7−8]，无需事先假定主滑面，计算过程更为简便，便于工程应用。同时，可以看出本文计算方法结果不同于属于极限平衡法范畴的文献[11−12]给出的结果，作者认为原因如下：1) 极限平衡法在进行稳定性分析解答时，需将滑体进行离散化，且对土条间的作用力的进行了假定，安全系数需要迭代计算，而本文方法基于最小势能原理，以滑体整体为研究对象，给出了法向力的显式解，无需迭代进行安全系数的计算；2) 本文方法与极限平衡法的建模假定不同，极限平衡法认为滑体整体为刚体，而最小势能法仅仅认为滑体内部不发生变形，但是在滑面上假定其为弹性，通过引入土弹簧模型进行建模分析。总体而言，最小势能法与极限平衡法应属于同一范畴内的分析方法，二者均是通过静力平衡关系建立安全系数求解模型，唯一不同的是二者求解法向应力的方式，致使2种分析方法呈现出不同的特点。

为了进一步探究影响边坡稳定性的因素，在保持=18.8 kN/m3不变的情况下，采用控制变量法研究其与土体的抗剪强度指标、滑面形态(即/的值)之间的关系，结果如图4所示。

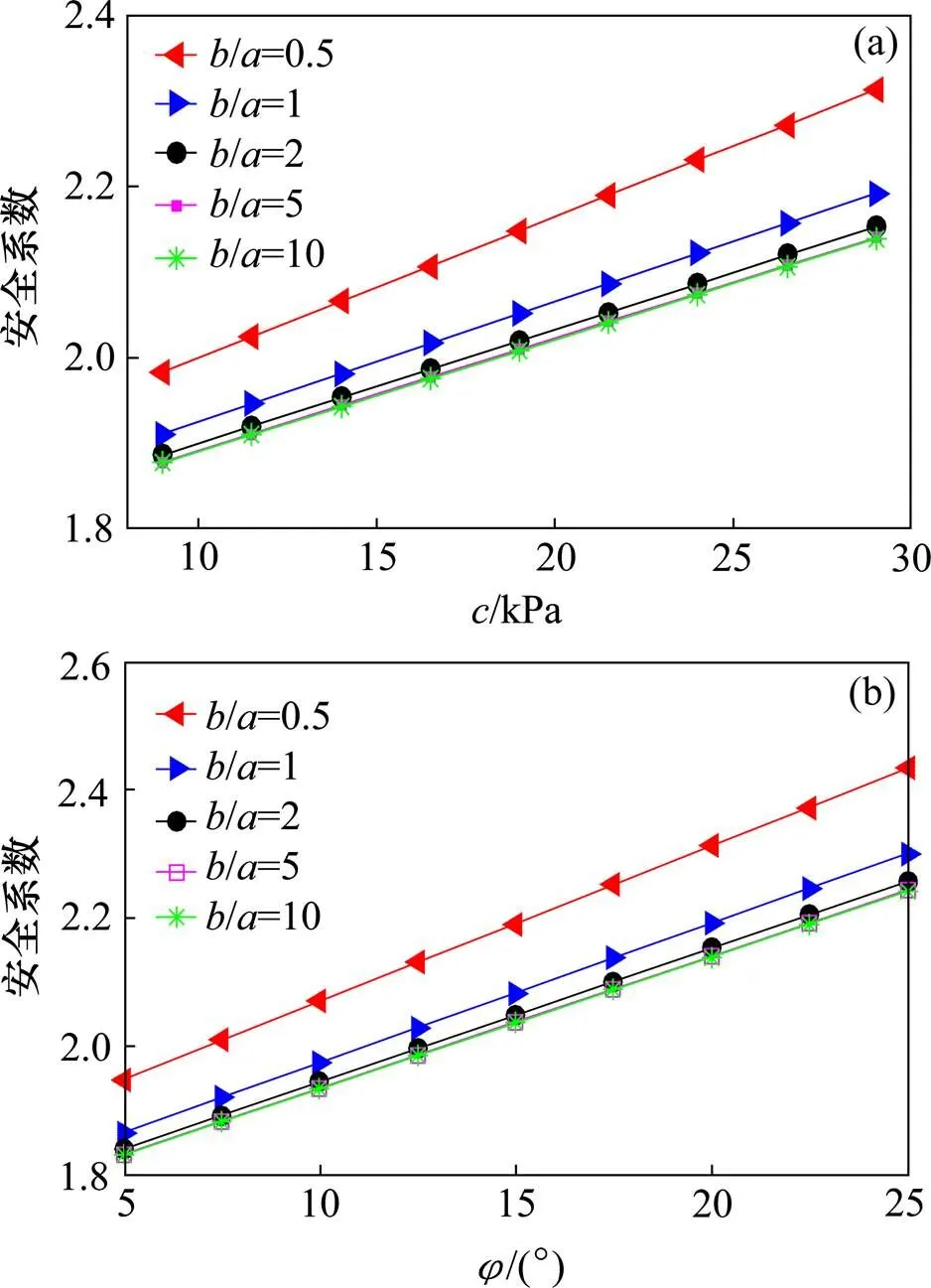
(a) φ=20°时；(b) c=29 kPa时

从图4可以看出：1) 土体的抗剪强度指标、滑裂面形态均影响着边坡的稳定性，其中随着抗剪强度指标的增加，边坡的安全性逐步增大，且呈二者之间呈线性关系；2) 滑裂面的形态对边坡安全性的影响较为显著，在/处于低水平时，边坡安全系数的计算结果较大。随着/的增大，安全系数呈现非线性降低的规律。当/≥5时，边坡的安全系数趋于稳定，即滑体横向宽度达到一定水平后，可将其视为平面应变问题进行分析，这与文献[15]的结论一致，表明文中计算方法的合理性。3) 应用理正岩土分析软件Bishop法计算可得，本算例的二维安全系数解答为2.090，而本文三维分析方法得到的结果为2.139(/=10时)，二者相对误差仅为2.3%。同时，可知本文的计算结果在略高于二维Bishop法，主要是由于三维的尺寸效应对计算结果的影响。由此可见，三维的分析结果会比二维的计算结果偏大，即二维的分析结果过于保守。同时，当三维滑体的横向尺寸较大时，三维尺寸效应对稳定性分析结果影响较小，可以将其视为平面问题进行处理。

3 结论

1) 三维边坡稳定性分析的最小势能法相比于原有的研究，在对剪切势能函数的建立、微面抗滑剪力的方向上具有以下2点不同：①通过滑体的整体静力平衡确定滑面上的剪应力函数，避免了划分条块时的条间力假定，降低了运算难度；②通过物体在斜面上的运动学规律，将微面的抗滑力方向假定为垂直于滑面与水平面的交线，避免了假定主滑面确定其抗滑方向，便于工程应用。

2) 将滑体整体运动方向视为微面抗滑方向矢量和的相反方向，借鉴矢量和法的思想定义边坡的安全系数，物理意义明确，相比于三维极限平衡法无需迭代计算。

3) 算例验证结果表明，本文的三维分析方法与其余算法的相对误差在10%范围内，满足计算精度要求，可以用于三维边坡的稳定性分析计算。

4) 土体的抗剪强度指标、滑面形态对边坡的稳定性存在影响，且边坡的稳定性随着，值的增大而线性提高。此外，当/≥5时，安全系数的计算结果与二维分析结果十分接近，表明此时可以将其简化为平面问题处理。

[1] Mauldon M, Ureta J. Stability analysis of rock wedges with multiple sliding surfaces[J]. Geotechnical & Geological Engineering, 1996, 14(1): 51−66.

[2] 李小强, 白世伟, 李铀. 最小势能方法在二维边坡稳定性分析中的应用[J]. 岩土力学, 2004, 25(6): 909−912. LI Xiaoqiang, BAI Shiwei, LI You. 2D slope stability analysis using principle of minimum potential energy[J]. Rock and Soil Mechanics, 2004, 25(6): 909−912.

[3] 温树杰, 孙加平, 梁超, 等. 改进的最小势能均质边坡. 稳定性分析方法[J]. 工业建筑, 2016, 46(3): 92−95. WEN Shujie, SUN Jiaping, LIANG Chao, et al. Analysis method of homogeneity slope stability based on improved minimum potential energy[J]. Industrial Construction, 2016, 46(3): 92−95.

[4] 李铀, 陆洋, 李妮, 等. 锚杆(索)加固边坡的最小势能稳定性分析方法研究[J]. 岩土力学, 2008, 29(9): 2329− 2334. LI You, LU Yang, LI Ni, et al. Research on stability analysis method for slope with anchors or prestressed-cables based on minimum potential energy principle[J]. Rock and Soil Mechanics, 2008, 29(9): 2329−2334.

[5] HU Guobao, SUN Hanzheng, WEN Shujie. Slope stability analysis and experimental study on 3D minimum potential energy method[J]. Electronic Journal of Geotechnical Engineering, 2015(23): 12379−12397.

[6] 温树杰, 宋亮亮, 梁超. 考虑桩体变形的最小势能边坡稳定性分析方法[J]. 工业建筑, 2017, 47(6): 90−94. WEN Shujie, SONG Liangliang, LIANG Chao. Stability analysis of slope with minimum potential energy considering pile deformation[J]. Industrial Construction, 2017, 47(6): 90−94.

[7] 温树杰, 罗惠, 李铀, 等. 基于最小势能原理的三维边坡稳定性分析[J]. 岩石力学与工程学报, 2015, 34(增1): 3298−3305. WEN Shujie, LUO Hui, LI You, et al. Three-dimension slope stability analysis based on minimum potential energy principle[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(Suppl 1): 3298−3305.

[8] 孙加平, 温树杰, 梁超, 等. 改进的三维边坡最小势能稳定性分析方法[J]. 中国安全生产科学技术, 2016, 12(1): 17−22. SUN Jiaping, WEN Shujie, LIANG Chao, et al. Stability analysis of three-dimension slope based on improved minimum potential energy[J]. Chinese Journal of Safety Science and Technology, 2016, 12(1): 17−22.

[9] 孙加平, 卜伟斐, 胡金木, 等. 二维边坡稳定性分析的最小势能法新解[J]. 力学与实践, 2017, 39(4): 349−353. SUN Jiaping, BU Weifei, HU Jinmu, et al. New solution of 2D slope stability analysis based on minimum potential energy principle[J]. Mechanics in Engineering, 2017, 39(4): 349−353.

[10] 袁恒, 罗先启, 张振华. 边坡稳定性分析三维极限平衡条柱间力的讨论[J]. 岩土力学, 2011, 32(8): 2453−2458. YUAN Heng, LUO Xianqi, ZHANG Zhenhua. Discussion on force between columns of three- dimensional limit equilibrium for slope stability analysis[J]. Rock and Soil Mechanics, 2011, 32(8): 2453− 2458.

[11] 郭明伟, 葛修润, 李春光, 等. 边坡和坝基抗滑稳定分析的三维矢量和法及其工程应用[J]. 岩石力学与工程学报, 2010, 29(1): 8−20. GUO Mingwei, GE Xiurun, LI Chunguang, et al. Three -dimension vector sum method employed in slope and dam foundation stability analysis and its application to practical engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 8−20.

[12] ZHANG X. Three-dimensional stability analysis of concave slopes in plan view[J]. Journal of Geotechnical Engineering, ASCE, 1988, 114(6): 658− 671.

[13] 孙加平. 改进的最小势能边坡稳定性分析方法及程序开发[D]. 赣州: 江西理工大学, 2016. SUN Jiaping. Improved minimum potential energy slope stability analysis method and program development[D]. Ganzhou: Jiangxi University of Science and Technology, 2016 .

[14] 陈祖煜, 弥宏亮, 汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525−529. CHEN Zuyu, MI Hongliang, WANG Xiaogang. A three-dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525−529.

[15] 李同录, 王艳霞, 邓宏科. 一种改进的三维边坡稳定性分析方法[J]. 岩土工程学报, 2003, 25(5): 611−614. LI Tonglu, WANG Yanxia, DENG Hongke. An improved method for three-dimension slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 611−614.

Study on minimum potential energy method for solving safety coefficient of three-dimensional slope

SUN Jiaping, WEI Xing, ZHAN Fengcheng

(Institute of Energy Technology, Jiangxi Vocational College of Industrial & Engineering, Piangxiang 337055, China)

In order to evaluate the stability of rock and soil effectively, the minimum potential energy method was used to analyze the stability of three-dimensional slope. The elastic compression potential energy and shear potential energy of the sliding body system were calculated by introducing the soil spring model and the overall static balance equation of the sliding body. At the same time, the sliding direction of the micro-plane was determined according to the law of motion of the object along the inclined plane under the action of gravity. The potential moving direction of the whole sliding body was regarded as the vector sum of the sliding direction of the micro-plane. Finally, the safety factor of slope was defined as the ratio of anti-sliding force to sliding force along the sliding direction. In order to verify the rationality of the calculation method in this paper, the safety factor of a classical example was calculated. The results show that the relative error between the solution and the other methods is within 10%, which indicates that the calculation method in this paper can be used for the stability analysis of three-dimensional slope. With the increase of the shear strength index of soil, the safety factor of slope presents a linear increase trend When the ratio of the lateral dimension to the longitudinal dimension of the three-dimensional sliding mass is greater than 5, the stability analysis of the three-dimensional slope can be treated as a plane strain problem.

slope; stability; minimum potential energy method; sliding direction; safety factor