一二维耦合水利枢纽施工导截流模型

林金波，金 生，门 亚，丁伟业

(1.大连理工大学 海岸和近海工程国家重点实验室，大连 116024；2.庄子建设集团(保定)有限公司，保定 071000)

在水利工程施工过程中，通常需要先截断原河道水流将河水引向导流泄水建筑物下泄，之后在排干的河床中进行主体建筑物的施工，这一构筑围堰截断河道水流从而形成施工基坑进行工程施工的过程叫做施工导截流。施工导截流是水利枢纽工程施工尤其是闸坝建设工程所特有的一项重要工程措施。导截流是水利工程施工的第一步，也是水利工程施工中的一个关键步骤，对后期的施工和使用都存在重要影响。另外，导截流的成功与否不仅影响水利水电工程的施工安全、施工工期及工程造价，还涉及坝址下游地区的防洪安全。因此，施工导截流在水利工程中是重要的关键项目之一，也是影响整个工程施工进度的一个控制项目。在导截流过程中，河道水力参数作为影响工程成败的主要条件，总是不断变化的。如果在实施导截流之前，能够通过一定方法得到龙口、河道及导流建筑物内的各项水力参数，尤其是对龙口断面形式、龙口尺寸及围堰体型和设计高程进行充分的实验研究和合理优化，就能对施工导截流的整个过程进行有效地控制，并对可能出现的不利情况，做好应急预案，从而在必要时采取及时有效的工程措施，以避免导截流失败或产生不必要的损失。因此，对施工导截流过程进行相关研究具有重要的理论与实际意义。

众多学者已经对水利工程导截流问题进行了大量研究，采用的研究方法多为模型试验[1-3]或数值模拟。特别是随着计算机技术的普及发展，越来越多的学者采用数值模拟方法进行导流问题模拟研究。其中，大多数通过求解二维浅水方程或NS方程，建立二维或三维导流模型进行数值模拟研究。胡春霞[4]、贺昌海[5]和王晓丽[6]分别采用有限差分方法、无网格伽辽金法及有限元方法建立了二维施工导流模型，对水利枢纽施工导流期间的河道流场进行了计算分析。对导流时通航水流条件、泄流能力、导流流场水力要素及围堰区水流流态等进行了较为系统化的研究。李扬[7]、贺昌海[8]和刘文[9]利用Fluent及Flow-3D软件，采用k-ε紊流模型及VOF自由表面追踪技术，建立了三维施工导流模型。利用三维模型对实际水利枢纽施工导流期间不同流量条件下的流场及冲刷进行了模拟分析，得到了受围堰影响变化后的河道水面线。另外，刘文[9]的施工导流三维模型中还考虑了泄水建筑物下泄水流中局部掺气的影响。赵瑜[10]、王继保[11]、麻夏[12]和陈九灵[13]建立了二维施工截流模型，并运用模型对戗堤立堵截流进行了数值模拟试验，探讨了立堵截流中戗堤的宽度效应，并对工程截流方案进行了优化分析。李飞燕[14]和汪淼[15]利用Fluent软件、有限体积方法建立了三维施工截流模型，对龙口断面的形式及单戗堤单向和双向立堵进占方式的水流条件进行了计算分析及优选。刘玉玲[16]和刘世伟[17]采用有限体积及有限元方法求解二维浅水方程,建立了二维导截流模型，并利用实际工程施工导截流模型试验的实测资料对模型进行验证。戴会超[18-19]结合三峡工程导流明渠通航, 开发了基于二三维耦合方法的施工导流模型。模型采用有限差分方法离散二维浅水方程模拟河道内大范围水域在施工导流过程中的流场演变过程,后由二维模型计算成果提供三维模型的边界条件及初始条件,给出导流过程关键部位的三维流速分布及水位分布。

由于某水利枢纽工程的特殊性，在二期导截流过程中需要通过一期已建成泄流低孔进行泄流。使得如果只通过求解二维浅水方程模拟二期导截流过程中泄流低孔部位过流时，所需网格尺度会非常小。这一方面造成网格数量过大，另一方面过小网格尺度又造成时间步长很小，最终使计算耗时过长。另外，三维模型虽然能够重现二期导截流河道及低孔流场，但其计算耗时也较长，不适合工程应用。为此，建立了一二维耦合施工导截流模型，通过求解二维浅水方程模拟河道及坝体表孔过流，同时通过求解一维过渡流方程模拟低孔过流。通过节点耦合的质量及动量守恒方法将一维及二维模型耦合求解，最终得到导截流过程中整个流场变化情况。

一二维耦合模型是一种非常有效的数值模拟工具，且已经被广大研究人员进行了一定研究应用。这种混合模型既保持了任何需要的地方的细节和精确性，同时与二维模型相比大大减少了时间消耗。但是，在已有的耦合模型中，大部分模型利用一维模型模拟河道、二维模型模拟洪水平原，通过耦合模型来求解河道洪水问题[20-21]。另有一小部分通过一维模型模拟城市排水管网及河流，二维模型模拟城市泛洪区，通过耦合模型求解城市雨洪问题[22-23]。然而，据作者所知，尚未有研究人员建立起一二维耦合的水利施工导截流模型。

采用交错网格结合半隐式离散的方法，在单元处对运动方程进行离散，在节点处对连续性方程进行离散，通过有限体积方法求解过渡流方程得到一维数值计算模型。二维模型采用非结构化网格离散计算域，并采用VC方式(Vertex-Centered)的有限体积方法离散二维浅水方程进行求解。一二维模型之间的连接采用节点耦合的质量及动量守恒方法实现。通过与物理模型试验测量水位、流速及流量进行对比，验证了耦合模型的可靠性。表明采用一二维耦合方法解决施工导截流问题是可行的，为类似导截流工程的流场计算及设计施工提供了一种新的技术手段。

1 数值方法

1.1 一维模型

明渠流与有压管道流是两种存在巨大差异的流动状态，因而在计算中,当出现明满交替流的情况时，由于二者之间的控制方程不一样，且明满流的分界面并不固定，会给计算造成极大的挑战。为此，很多学者对一维明满流模型的计算进行了深入的研究，其中基于Preissmann狭缝假设[24]的隐式差分方法由于其算法简单，计算程序容易实现等优点而实际应用最广。

(1)

(2)

式中：Q为流量；v为流速；Sf为摩阻坡度；SL为局部水头损失。

一维过渡流控制方程离散采用交错网格和半隐式离散方法，对河道(管段)上的运动方程和节点上的连续性方程进行离散。这种离散格式不仅保证了离散格式的守恒性和稳定性，而且便于计算数据的输入。详细离散方法见文献[25]。

1.2 二维模型

对于二维平面上的大范围自由表面流动，其垂向尺度通常远小于平面上的尺度，此时可以引入浅水假设将守恒方程进行简化。假设垂向上的压强分布服从静水压强的分布规律，同时对基本的连续性与动量守恒控制方程沿深度方向积分以引入平均化处理，再经过一系列的推导即可得到平面二维浅水方程的一般形式

(3)

(4)

(5)

采用有限体积法对连续方程进行离散，以保证离散格式的守恒性。同时，由于二维浅水方程的旋转不变特性，在网格单元的边和其法向(单元中心)形成局部坐标系下离散运动方程。二维计算域的离散采用非结构化网格。非结构化网格具有较好的边界拟合性，对复杂几何边界适应性强，局部细化更加灵活。具体离散方法见文献[26]。

1.3 模型耦合

一维模型与二维模型通过节点连接，将耦合节点分别作为一维模型和二维模型的内边界，以实现一维模型和二维模型间的相互作用。一维模型及二维模型间的流场信息交换，采用一个能够保证质量和动量同时守恒(MMC)的方法[27]。该方法在耦合的一维节点和二维节点施加相同的水位。其中，水位采用严格的质量守恒法计算。

耦合边界的总流量可以表示为

(6)

(7)

式中：

(8)

(9)

对于动量守恒，引入一个流向角度，将一维模型内的流量表示为矢量，以实现一二维模型间的动量交换。

QIDx=QIDcosα

QIDy=QIDsinα

(10)

与质量守恒处理过程类似，动量的大小和方向可以表示为

(11)

(12)

然后，x、y方向的平均速度U、V可以根据耦合区的总流量Vc计算得到

VcU=MxVcV=My

(13)

最终，守恒变量通过下式更新

(14)

2 模型验证

为了验证一二维耦合模型精度，采用某水利枢纽二期截流工程试验数据与数值模拟结果进行对比分析。根据枢纽坝址区的地形条件，结合水工构筑物布置，将该枢纽施工导流划分为两期。一期导流先施工左岸，利用右岸河道束窄后的河床过流；二期导流施工右岸，并利用一期工程建设的1孔泄流高孔及20孔泄流低孔宣泄流量。

图1 河道及枢纽平面布置图

水利枢纽二期截流工程中大范围河道及泄流高孔利用平面二维模型，采用非结构化网格离散。通过一维模型模拟泄流低孔。模型面积为10.8 km2。网格尺度取30 m。局部纵向混凝土围堰、戗堤附近、过流表孔附近及船闸引渠附近，由于结构尺寸较小，采用30 m网格无法表达建筑物结构特征，故需对局部网格进行加密，坝体、纵向围堰及船闸引渠部分加密网格尺寸为10 m，戗堤区域网格尺寸为5 m。一维过流低孔通过20条线段进行模拟，网段划分尺度取为100 m，每一低孔划分为一个网段；共20个网段，40个节点。河道及枢纽平面布置见图1。水位初值取为30 m。糙率取为0.025。一维网段初始流量为0。模型上游边界条件设置流量边界。模型下游边界距离坝轴线约为5 km，故采用坝下5 km位置河道水位-流量关系作为下游边界。时间步长取为1.8 s。

表1 枢纽工程二期截流试验数据与数值结果对比

实验数据来自按重力相似准则设计、比尺为1:80的室内物理模型实验。试验设计流量为1 050 m3/s。一期围堰拆除至25 m高程。针对不同龙口宽度分别进行了物理模型实验，实验成果见表1。由表1可知，数值模型计算水位误差较小，水位最大误差为0.09 m，分流比最大误差3.1%。模型计算龙口最大流速误差较大，其原因可能是受到网格精度影响，最大流速误差0.88 m/s，相对误差15.6%。综上可知，模型计算结果与实验数据吻合良好，模型适用于水利枢纽导截流工程模拟。

3 模型应用

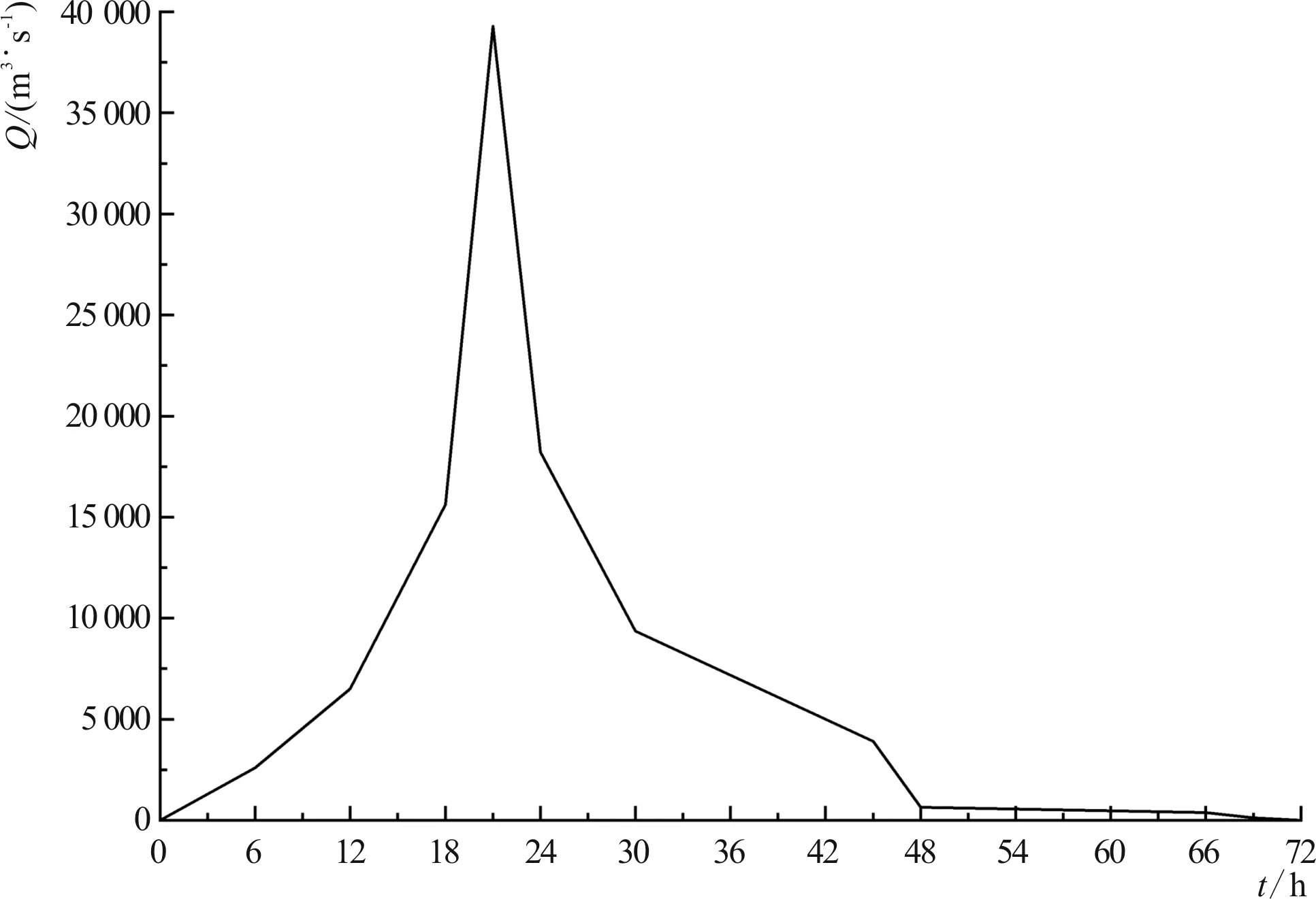
图2 上游边界入流流量过程

将模型应用于第2章内水利枢纽的二期导截流工程，对施工导流过程中河道及泄流低孔内水位及流速变化进行模拟分析。模型入流边界条件设置为一入流流量过程(图2)。该流量过程为工程附近水文站3 d降雨过程同比例放大得到的洪水过程，其中最大流量值为20 a一遇设计流量39 300 m3/s。模型上游边界条件设置为该流量过程。下游边界同样采用坝下5 km位置河道水位-流量关系。时间步长1.8 s，推进步数144 000，共模拟72 h流场变化过程。

图3给出了水利枢纽施工导流流场。t=0 h时，右岸束窄河道内初始水位为30 m，流速为零；随后，由于上游入流尚未到达坝址处，坝址处水位持续降低，流速增大；直到t=3 h，一期泄流低孔内已无过流，上游来流全部从右岸束窄河道流向下游；随着上游入流到达坝址，坝址位置水位逐渐升高；t=6 h，泄流低孔内重新过流；之后，坝址位置水位及流速持续增加；直到t=21 h，洪峰到达坝址，坝址水位升高到最大值，最高水位约42 m，右岸束窄河道内流速最大值约7 m/s；洪峰流量通过后，流量逐渐减小，河道内水位及流速逐渐降低；t=48 h，坝址处水位下降到一定值，来流全部通过右岸束窄河床向下游宣泄，低孔内无水流过流；t=72 h，水位流速降到最低值，一期围堰未拆除部分完全露出水面。

图4为河道中心附近10#泄流低孔水位和流速过程，图中h为水位，zb为低孔底高程，zt为低孔顶高程。低孔内水位变化趋势与入流量趋势基本一致；模拟开始后上游入流尚未到达低孔，低孔内水位逐渐下降；直到t=3 h水位下降到最低值24.545 m后开始逐渐上升；t=21 h水位达到最大值42.065 m；随后，水位逐渐降低直到t=72 h水位值下降到22.536 m。t=21 h以前低孔内水位低于40 m为明渠流态；t>21 h后低孔内水位高于40 m为有压流；t=24 h低孔内水位为37.819 m低于孔顶高程40 m，低孔内恢复为明渠流态。模型能够合理重现低孔内明满流过渡过程。低孔内流速变化趋势同样与入流量趋势基本一致；t=0 h，低孔内初始流速为0 m/s；由于上游入流需一定时间才能到达坝址处，使低孔内水位先下降后上升，造成低孔内流速先稍有升高，在t=1 h达到0.12 m/s后再次下降并维持较低值；t=6 h后，流速迅速增大；直到t=21 h，低孔内流速达到最大值2.14 m/s；然后，随着流量减小，低孔内流速迅速降低；直到t=48 h，降低到0.1 m/s以下。

3-at=0 h 3-bt=3 h 3-ct=6 h

3-dt=21 h 3-et=48 h 3-ft=72 h

图3 水利枢纽施工导流流场

Fig.3 Construction diversion flow field of the hydro-junction project

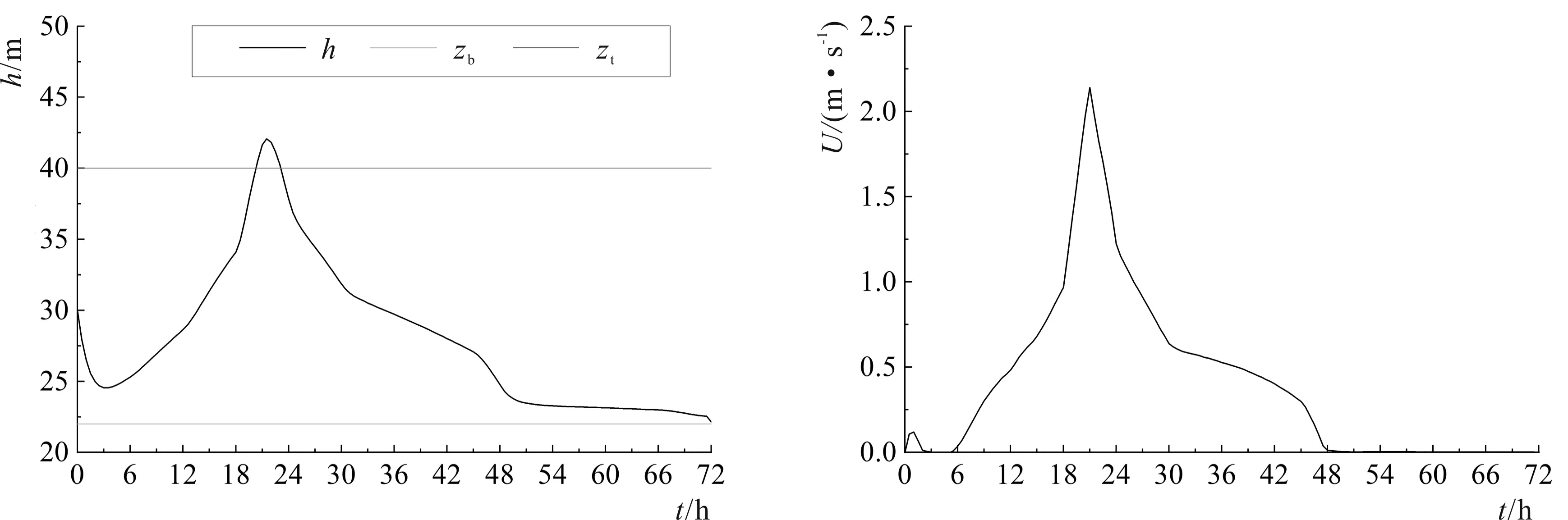
4-a 水位 4-b 流速

图4 10#泄流低孔水位与流速过程

Fig.4 Water level and velocity of the discharge low hole 10#

4 结论

利用有限体积方法建立了一二维耦合施工导截流模型，并利用该模型建立了某水利枢纽二期截流数值计算模型，将模型计算水位、流速及流量值与模型试验数据进行对比，模型能够精确模拟施工导截流流场水利参数。利用耦合模型对峰值为20 a一遇设计流量39 300 m3/s的入流过程水利枢纽施工导流河道和泄流低孔内的水位和流速进行了数值模拟分析。当入流流量较小时，上游来流可通过右岸束窄河床导向下游，泄流低孔内无水流流过；当流量较大时，右岸束窄河床与泄流低孔能够联合泄流，将来流宣泄入下游河道。河道和泄流低孔内水位最大值约42 m，河道内最大流速为7 m/s，低孔内流速较河道内更小，最大流速2.14 m/s。另外，模型还能够合理重现泄流低孔内明满流过渡过程。本文为类似导截流工程的流场计算及设计施工提供了新的技术手段。一二维耦合模型的不足之处在于采用一维模型模拟低孔内水流流动，而低孔内流动实际上具有三维特征。因此，建立二三维耦合模型，采用三维模型模拟低孔内流动所得计算结果可能更加准确。