海底振动管道局部泥沙冲刷数值研究

2020-06-08刘名名郭晓玲

水道港口 2020年2期

殷俊，刘名名，冀昊，金鑫，郭晓玲

(1.国家电投集团广东电力有限公司，广州 510130；2.成都理工大学能源学院，成都 610059;3.水电水利规划设计总院，北京 100120;4.国家知识产权局专利局专利审查协作天津中心，天津 300304)

海底管道作为一种高效、经济的海上输运方式，在海洋油气资源开发中得到广泛应用。海底管道周围的泥沙颗粒在水流作用下将产生输运，泥沙颗粒的运移会在管道周围形成冲刷坑。冲坑的存在将严重影响海底管道的在位稳定性。

1 前言

长期以来研究者主要以物理实验和数值模拟两种方法对海底管道局部冲刷问题进行研究。受限于计算机模拟技术，早期的研究主要集中在物理实验研究方面，如Mao[1]，Ibrahim和Nalluri[2]，Sumer等[3]，Fredsøe等[4]以及Chiew等[5]的研究工作。上述试验结果表明：海底管道局部冲刷特性与来流流速、管道直径、水深以及泥沙粒径密切相关，并建立了相关经验公式预报海底管道的冲刷特性。这些开拓性研究工作，极大地加深了人们对海底管线局部冲刷的认识。

20世纪80年代起，众多学者开始采用数值模拟对海底管道局部冲刷问题开展研究工作。Hansen等[6]基于无粘、无旋假设，建立了海底管道局部冲刷势流数值分析模型，由于无法考虑流体的粘性效应，导致数值模拟结果与试验结果存在较大差异。为克服势流理论数值分析模型缺点，Beek和Wind[7]建立了基于N-S方程的数值分析模型，结合标准k-ε湍流封闭模型，实现了对海底管道附近泥沙输运的模拟，模拟结果表明：数值模拟得到的数据在冲刷趋势上与实验室结果吻合较好，但是数值结果与实验室结果在管道周围底床剖面形态上存在较大差异。此后，Li和Chengi[8]采用N-S方程和大涡模拟的方法，对海底管道局部泥沙冲刷问题进行了数值研究。在后续研究工作中，Li和Cheng[9]将上述数值模型拓展到管道自沉的数值模拟研究工作，相关数值分析模型得到了令人满意的结果。此后，Liu等[10]以及刘名名等[11]成功通过求解利用SSTk-ω湍流模型封闭的Navier-Stokes方程组，实现了对海底管道在波浪作用下产生的局部泥沙冲刷的模拟。相关的研究结果表明，SSTk-ω湍流模型可以实现对涡流场及近壁区高流速梯度的准确模拟，进而保障海底管道局部泥沙冲刷的准确性。

但是实际的情况为：海底管道发生局部冲刷后，冲坑会沿着管道轴向方向不断扩展，从而形成悬空管道。在周期性交变流体力作用下，悬空管道会发生涡激振动，尤其当管道后方的涡脱落频率接近于悬跨段的固有频率时，会发生“锁定”(Lock-in)现象。目前，针对振动管道局部泥沙冲刷的研究工作比较少，并且研究对象均为实验室小直径管道。开拓性研究工作为Sumer等[3]的试验研究工作。在Sumer等[3]的试验中，管道只允许发生横流向振动，研究其周围泥沙冲刷状况。在此基础上，Shen等[12]对具有x、y两个自由度的海底管道在水流作用下的局部泥沙冲刷问题进行了实验研究。Yang等[13]通过实验手段对管道振动与泥沙局部冲刷的耦合作用进行了研究。Gao等[14]和沙勇等[15-16]同样利用实验手段对振动管道在水流作用下的局部泥沙冲刷问题进行了研究。张玮等[17]和孙国民等[18]也对水流作用下的海底管道冲刷问题开展了研究。

需要指出的是：上述物理模型实验由于难以得到详细的流场流动结构，所以未能给出流场、管道振动以及泥沙输运之间的耦合作用机理。Zhao和Cheng[19]建立起一套通过求解不可压缩粘性牛顿流体的Navier-Stokes方程、简化的弹簧阻尼约束下的结构运动方程以及泥沙颗粒运动方程的有限元模型。通过该模型对实验室尺寸的振动管道在水流作用下泥沙局部冲刷问题展开了数值模拟。研究结果表明：管道振动引起的最大冲刷深度较固定管道情况下大25%。

从以上的内容可以看出，振动管道局部泥沙冲刷较固定管道情况下局部泥沙冲刷有较大的差别。但是在现在已发表的文献中仅有对实验模型尺寸管道局部泥沙冲刷的研究。而对于原型尺寸振动管道局部泥沙冲刷的研究工作尚未见报道。本文将对原型尺寸下管道振动、泥沙颗粒运动以及底床变形耦合问题展开研究工作。

2 数值模型

2.1 流体运动控制方程

本文采用的流体运动控制方程为Navier-Stokes方程组。为描述由于管道振动以及底床变形引起的网格位置变化，本文采用ALE方法对变形网格位置进行追踪，ALE参考坐标系下流体运动控制方程可以表示为

(1)

(2)

(3)

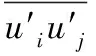
(4)

式中：υt为湍流引起的粘性系数，k为特定的湍动能，δij为Kronecker函数。本文采用SST(Shear-Stress Transport)k-ω湍流模型求解k。具体方法及参数设置可参考Menter[20]以及Menter[21]等的文献。

2.2 泥沙运动控制方程

本文采用的泥沙冲刷模型，同时考虑推移质和悬移质输沙对冲刷的影响。在悬移质输沙模型中，泥沙浓度的扩散控制方程为

(5)

式中：c为泥沙在水体中的浓度，ws为泥沙在水中的沉降速度，σc为常数，本文取σc= 1.0。泥沙在水中的沉降速度通过下式计算

(6)

式中：ds为计算采用泥沙的中值粒径，D*为无因次后泥沙颗粒的粒径，可以写为

D*=[g(s-1)/v2]1/3ds

(7)

推移质输沙率采用如下的计算公式，相关表达式为

(8)

式中：qb为计算域中单宽输沙率，s=ρs/ρ为泥沙颗粒的密度与水流密度的比值，ρs为计算采用的泥沙颗粒的密度。Shields参数(θ)可以写成如下的形式

(9)

式中：u*为底摩阻流速。

通过如下的方法对底床坐标进行更新

(10)

式中：yb为海床的垂向坐标值，ps为计算采用的泥沙颗粒的松散度。系数C在本文中取为2.0。

2.3 管道运动方程

管道横向振动方程可表示为

(11)

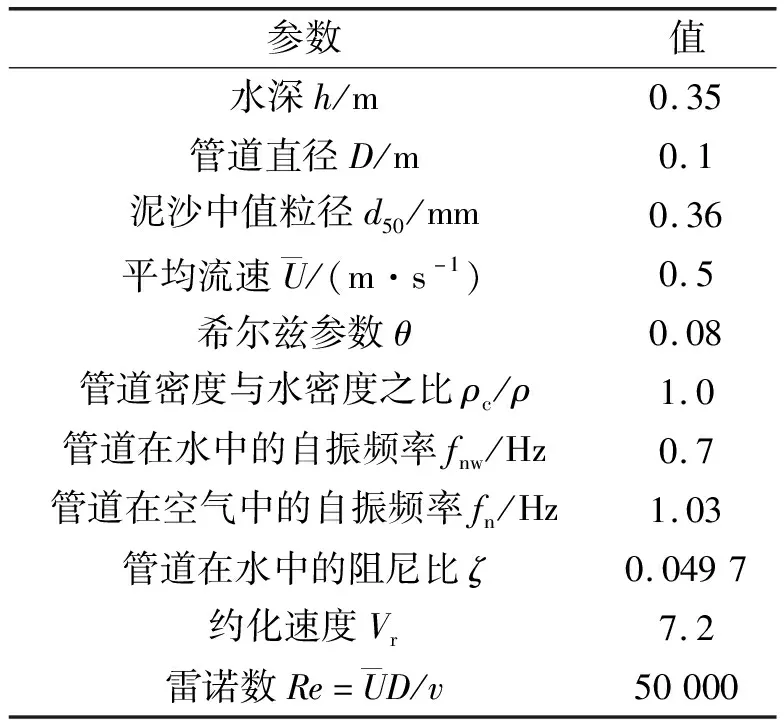
表1 计算参数表

3 数值模型验证

Sumer等[3]对水流作用下振动海底管道的局部冲刷问题进行了实验研究。为验证本文所建数值模型的正确性，本文首先对单向流作用下振荡管道周围的冲刷问题进行计算，并与实验结果进行了比较。相关计算参数如表1所示。

图1给出了不同时刻管道周围泥沙冲刷剖面图。图1-a给出了t= 30 min时，管道周围泥沙冲刷的剖面形态。从图1-a的对比图中可以发现，本文所建数值模型得到的数值结果与Sumer等[3]实验得到的实验结果具有较高的吻合性。这种吻合性不仅仅体现在冲刷深度上，同时还体现在冲坑的形态上。这表明本文所建立的模型能够较好地预测振动管道周围的泥沙冲刷情况，进而说明本文所建立数值模型可以用来对振荡管道周围的泥沙冲刷问题进行研究。

1-at=30 min 1-bt=243 min

图1 管道局部冲刷剖面图

Fig.1 Sectional scouring section of the pipeline

图1-b给出了t= 243 min时，管道周围的泥沙冲刷剖面形态。从图中可以发现，数值模拟结果与实验结果吻合良好。从而证明本文建立的模型可以用来对振荡管道周围的冲刷过程进行预测。对比图1-a和图1-b可以发现，从t= 30 min到t= 243 min管道下方的最大冲深增加不多。但是管道周围的冲刷剖面改变较大。这与要体现在(a)管道下游剖面更加平缓(b)管道上游和下游的过渡段增长。

表2 计算参数

4 计算结果与分析

通过上文的验证可知，本文所建数值模型能够较为准确地预测振动海底管道局部冲刷。本文对直径为1.0 m的振动海底管道在1 m/s的流速下的局部泥沙冲刷问题进行研究。具体的计算参数如表2所示。由于管道的振动会导致管道接触到海床，在本文的计算过程中当管道距离海床表面的最小距离小于5 cm时，认为管道与海床接触并强制管道的速度为0 m/s。

4.1 振动位移

图2给出了振动位移时间历程线。从图中可以看出管道的最大振动位移大约为0.8倍的管道直径。管道位移在时间上可以分为如下的4个阶段：

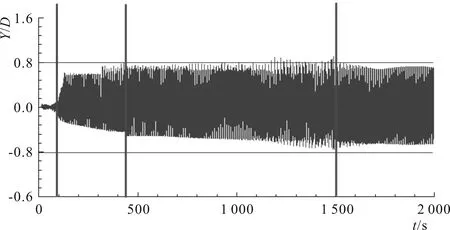
图2 管道位移时间历程线

(1)大约0～100 s时，管道振动幅值较小并且逐步增大。

(2)大约100～450 s时，管道振幅逐步增大，最大振幅增大到约为0.8倍管道直径，并且管道正向振幅明显大于负向振幅，在此阶段管道运动会接触底床。

(3)大约450～1 500 s，管道正向振幅近乎不变而负向逐步增大到约0.7倍管道直径。在此阶段管道运动也会接触底床。

(4)大于1 500 s，管道振动幅值近乎稳定。

4.2 冲刷深度及剖面

图3 管道局部冲刷剖面

图3给出了固定管道以及振动管道平衡状态下管道局部泥沙冲刷剖面对比图。从图中可以看出，在本文的计算范围内振动管道的冲坑形态较固定管道时有较大的不同，具体体现在以下4个方面。

(1)振动管道最大冲刷深度较固定管道情况下最大可高50%。

(2)振动管道的最大冲刷深度位于管道后方而非管道正下方。

(3)振动管道后方冲刷范围和冲刷深度明显高于固定管道的情况。

(4)振动管道前方冲刷深度和冲刷范围较固定管道情况下小。

4.3 涡脱落形式各个阶段的尾涡脱落形式

由上文的讨论可见振动管道情况下的局部泥沙冲刷较固定管道情况不同。图4给出了直径为1.0 m的固定海底管道，在1 m/s的流速下的局部冲刷平衡时，固定管道局部涡脱落情况。图4-a～4-d分别对应着固定管道所受升力最小值、零、最大值和零时刻管道局部涡脱落情况。图5给出了振动管道局部涡脱落情况。图5-a～5-d分别对应着振动管道位移最小值、零、最大值和零时刻管道局部涡脱落情况。

4-a min 4-b zero

4-c max 4-d zero

图4 固定管道局部涡脱落情况

Fig.4 Local vortex shedding of fixed pipeline

从图4中可以看出在一个升力周期内，管道后方有一对涡脱落。并且总体上涡是沿着水流方向脱落的。尾涡的最大长度约为管道直径的2.0倍。从图5-a中可以发现，此时管道周围有正向涡A1脱落，同时存在正向涡A和负向涡B。从图5-b中可知，当管道继续向上运动时，负向涡B向下运动并变长，正向涡A从管道上脱落下来。当管道运动到位移最大处时，负向涡B分裂成涡B和涡B1。如图5-c和5-d所示，当管道向下运动到原位置时，负向涡B脱落。从而在管道后方形成由涡A1和涡B组成的一排涡以及由涡A和涡B1组成的另一排涡。在本文的计算条件下，从整体上讲，振动管道局部的涡长度较固定情况下短，这使得振动管道后方底床切应力大于固定管道的情况，进而导致振动管道后方冲刷深度较固定管道情况下深。