目标运动要素误差对尾流自导鱼雷齐射影响

王顺杰，张玉玲，罗向前

(海军潜艇学院，山东 青岛 266199)

潜艇鱼雷射击误差主要包括鱼雷散布和目标散布。其中，目标散布是影响鱼雷射击精度的主要因素，其主要是由于目标运动要素误差引起的。通常情况下，当目标运动要素误差不大时，自导鱼雷单雷射击能够满足命中概率指标要求。但在实际过程中，由于解算目标运动要素需要一定时间，且与声呐探测性能、海洋环境等因素有关，因此，一般情况下没有准确的目标运动要素［1］。当目标运动要素误差较大时，为了能够遮盖目标散布，提高对目标的命中概率，可组织双雷雷齐射，保证至少有1条命中目标。

目前，国内学者对鱼雷齐射问题进行了一定的研究［2-6］，但未见有关于目标运动要素误差对尾流自导鱼雷齐射影响方面的相关文献资料。由于在自导鱼雷发射之前要进行目标运动要素解算，是否等要素完全收敛再发射鱼雷，还是可以容忍一定的要素误差，因此就需要对目标运动要素误差对射击效果的影响进行分析。

本文主要研究目标运动要素误差中各误差对尾流自导鱼雷齐射的影响程度，从而为相关岗位人员在使用尾流自导鱼雷时提供一定的参考，达到提高鱼雷捕获目标尾流概率的目的。

1 尾流自导鱼雷平行航向齐射组织方法

如图1所示，尾流自导鱼雷平行航向齐射时，两雷完成出关直航后，先以一定的散角α 展开至预定的鱼雷间隔dk，再分别执行二次转角ω21和ω22，回转到鱼雷中线航向Bg+φ 上，然后两雷以平行的航向搜索目标尾流。在鱼雷搜索到目标尾流之前，两雷将沿平行航向保持直航，直至尾流自导装置捕获目标尾流。

图1 尾流自导鱼雷齐射攻击示意图

齐射各雷的执行的一次转角ω1i(i=1，2)为齐射中线瞬时转角ω 与散角展开角的代数和，即

式中，i=1，符号取“+”，i=2，符号取“-”。

而齐射各雷的二次转角大小相同、符号相反，分别向鱼雷中线转过0.5α。

2 尾流自导鱼雷平行航向齐射数学模型

2.1 齐射扇面中线参数求解模型

尾流自导平行航向齐射扇面中线是以尾流自导鱼雷单雷射击为基础的。

如图2所示，以发射鱼雷时刻目标位置点Mg点为原点，Y轴平行于鱼雷执行完一次转角后的航向Cl，X轴垂直于Y轴建立直角坐标系，则尾流自导鱼雷转角射击方程为［7］

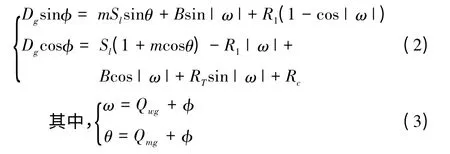
式中，Dg为射距;Sl为鱼雷航程;φ 为提前角;θ 为命中角;ω 为鱼雷转角;Qwg为我舷角;Qmg为敌舷角;B为鱼雷出管直航段;R1为鱼雷旋回半径;m为速率比;Rc为目标走完进入距离Dw时间内鱼雷航行的距离，其公式表达式为Rc=Dw/m。

通过以上两式可求解出鱼雷中线转角ω。

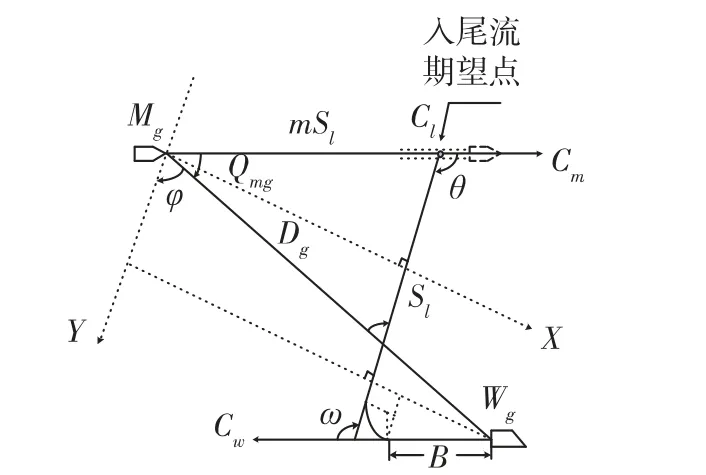
图2 尾流自导鱼雷射击参数解算示意图

2.2 齐射鱼雷二次转角前直航距离

目前，当采用计算提前角射击时，齐射鱼雷散角为某一固定值，鱼雷间隔本身不属射击控制诸元，但当鱼雷齐射散角确定后，其是计算鱼雷二次转角前直航距离的依据。如图1所示，鱼雷二次转角前直航距离可通过以下公式求解:

2.3 齐射鱼雷间隔

目前，当采用计算提前角射击时，尾流自导鱼雷齐射鱼雷间隔由系统自动计算，其计算公式为

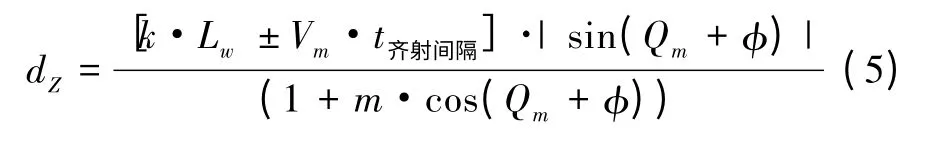
式中:Lw目标有效尾流长度;k为控制鱼雷进入尾流点的比例系数;顺序发射时符号取“-”，逆序发射时符号取“+”。

目标尾流长度计算公式为

3 尾流自导鱼雷平行航向齐射仿真分析

情况想定条件:海况3级，目标方位050 °，距离30 cab～50 cab，发射目标舷角40 °～110 °，目标速度16 kn(20 kn)，鱼雷速度40 kn，鱼雷速度均方误差1 kn，鱼雷航向均方误差1 °，目标方位均方误差0.3 °。

单雷成功捕获目标尾流条件:当鱼雷进入尾流点到目标舰尾的长度Dw满足式(7)、鱼雷进入尾流角θ满足式(8)时，认为鱼雷成功捕获目标尾流。

3.1 仅存在目标速度误差时

假设仅存在目标速度误差，图3至图5分别是目标速度16 kn，射距30 cab、射距40 cab和射距50 cab时不同目标舷角条件下鱼雷捕获目标尾流概率。各图中上图的目标速度均方误差为1 kn;中图的目标速度均方误差为2 kn;下图的目标速度均方误差为3 kn。

从图3至图5中可以看出，在不同的射距条件下，随着目标速度误差的增大，不同目标舷角条件下对2雷同时捕获概率影响均较大;对至少1雷捕获概率有一定的影响，且目标舷角越大影响越大。

图6是目标速度20 kn，射距40 cab时不同目标舷角条件下鱼雷捕获目标尾流概率。比较图6和图4，只是仿真的目标速度有所不同，该仿真条件下也满足以上分析的变化规律。

3.2 仅存在目标航向误差时

假设仅存在目标航向误差，图7至图9分别是目标速度16 kn，射距30 cab、射距40 cab和射距50 cab时不同目标舷角条件下鱼雷捕获目标尾流概率。各图中上图的目标航向均方误差为2 °;中图的目标航向均方误差为8 °;下图的目标航向均方误差为15 °。

从图7至图9中可以看出，在不同的射距条件下，随着目标航向误差的增大，不同目标舷角条件下对2雷同时捕获概率影响均较大;对至少1雷捕获概率有一定的影响。且影响程度都是随目标舷角的增大先减小后增大，当目标舷角80°～90°时影响最小。

图3 射距30 cab，敌速16 kn时，仅存在不同速度误差条件下鱼雷捕获目标尾流概率

图4 射距40 cab，敌速16 kn时，仅存在不同速度误差条件下鱼雷捕获目标尾流概率

图5 射距50 cab，敌速16 kn时，仅存在不同速度误差条件下鱼雷捕获目标尾流概率

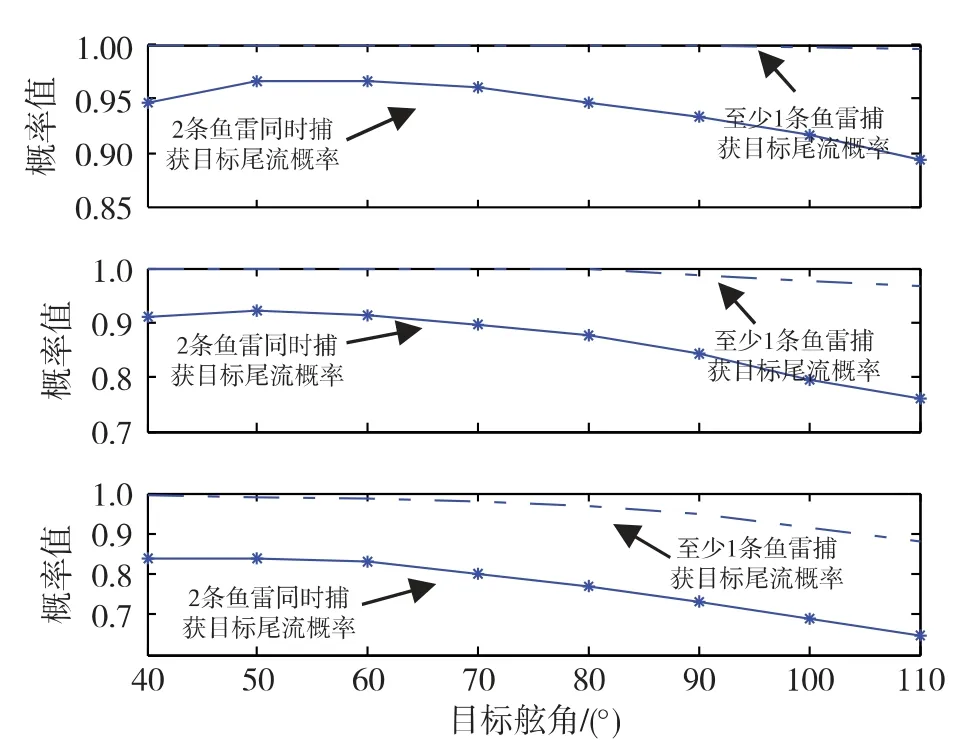
图6 射距40 cab，敌速20 kn时，仅存在不同速度误差条件下鱼雷捕获目标尾流概率

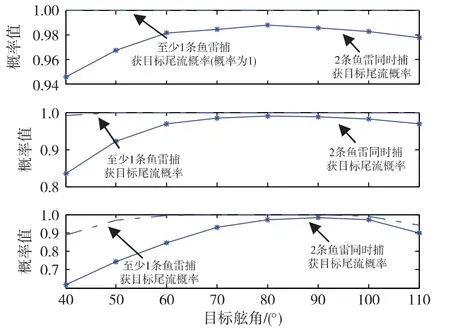
图7 射距30 cab，敌速16 kn时，仅存在不同航向误差条件下鱼雷捕获目标尾流概率

图8 射距40 cab，敌速16 kn时，仅存在不同航向误差条件下鱼雷捕获目标尾流概率

图9 射距50 cab，敌速16 kn时，仅存在不同航向误差条件下鱼雷捕获目标尾流概率

图10是目标速度20 kn，射距40 cab时不同目标舷角条件下鱼雷捕获目标尾流概率。比较图10和图8，只是仿真的目标速度有所不同，该仿真条件下也满足以上分析的变化规律。

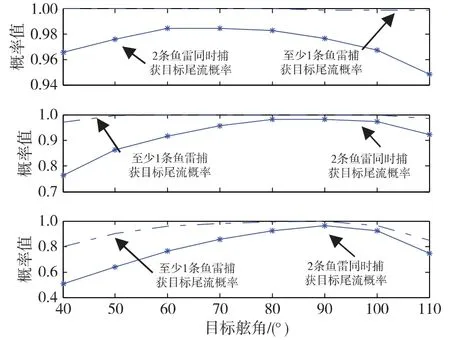
图10 射距40 cab，敌速20 kn时，仅存在不同航向误差条件下鱼雷捕获目标尾流概率

3.3 仅存在目标距离误差时

假设仅存在目标距离误差，图11至图13分别是目标速度16 kn，射距30 cab、射距40 cab和射距50 cab时不同目标距离条件下鱼雷捕获目标尾流概率。各图中上图的目标距离均方误差为10%Dg;中图的目标距离均方误差为15%Dg;下图的目标距离均方误差为20%Dg。

从图11至图13中可以看出，在不同的射距条件下，随着目标航向误差的增大，对2雷同时捕获概率和至少1雷捕获概率有一定影响，但都很小。

图14是目标速度20 kn，射距40 cab时不同目标舷角条件下鱼雷捕获目标尾流概率。比较图14和图12，只是仿真的目标速度有所不同，该仿真条件下也满足以上分析的变化规律。

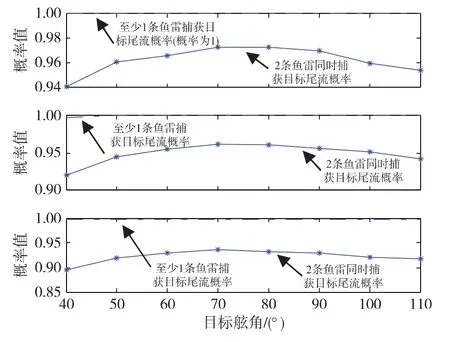
图11 射距30 cab，敌速16 kn时，仅存在不同距离误差条件下鱼雷捕获目标尾流概率

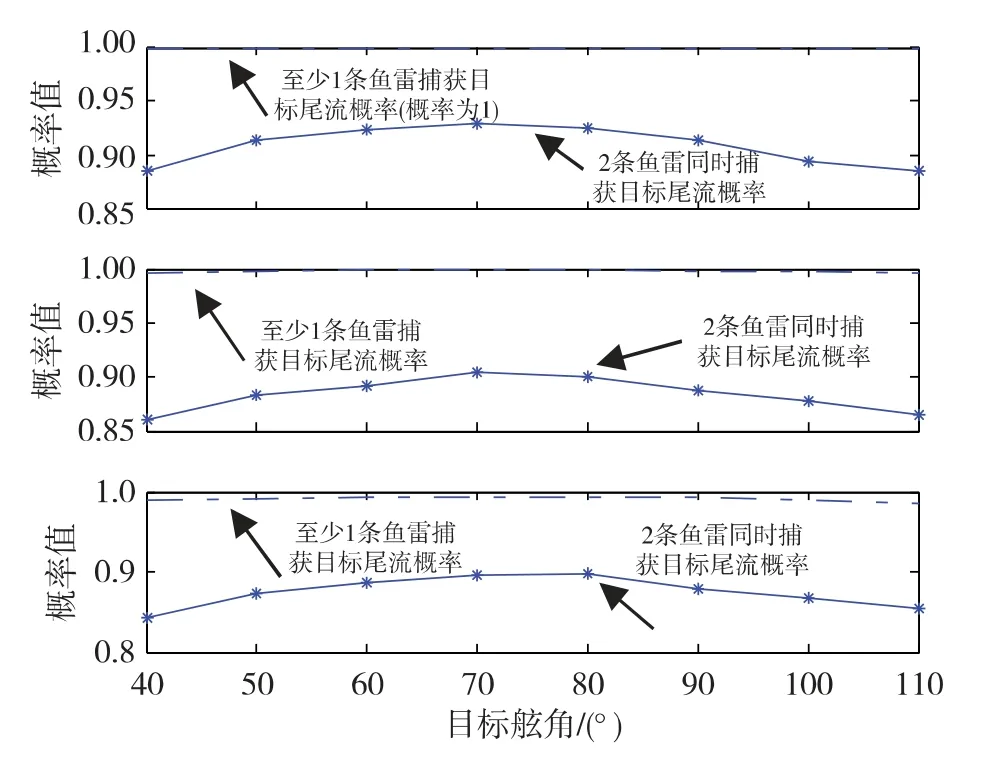
图12 射距40 cab，敌速16 kn时，仅存在不同距离误差条件下鱼雷捕获目标尾流概率

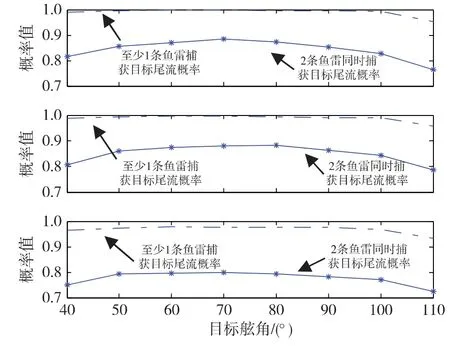
图13 射距50 cab，敌速16 kn时，仅存在不同距离误差条件下鱼雷捕获目标尾流概率

图14 射距40 cab，敌速20kn时，仅存在不同距离误差条件下鱼雷捕获目标尾流概率

3.4 存在目标要素综合误差时

一般情况下，目标速度误差、航向误差、距离误差同时存在。假设目标速度16 kn，射距40 cab，当存在综合误差时，仿真设置以下5种条件，如表1所示。

表1 仿真条件设置情况

表2为仿真结果，当目标舷角40°～50°时，目标航向误差对鱼雷捕获目标尾流概率影响最大，主要是由于目标航向误差导致鱼雷进入尾流角不满足要求，其次目标速度误差对结果也有一定影响，导致条件5情况下2雷同时捕获尾流概率和至少1雷捕获尾流概率都很低。

当目标舷角60°～110°时，目标速度误差对鱼雷捕获目标尾流概率影响最大，当目标舷角超过100°时，目标航向误差对结果影响快速增大。

当目标舷角70°～90°时，2雷同时捕获尾流概率和至少1雷捕获尾流概率总体相对较高。

4 结束语

本文对目标运动要素误差对尾流自导鱼雷齐射影响进行了研究。通过分析，可以得到以下结论:

1)在仿真条件下，当目标舷角40°～50°时，目标航向误差是影响尾流自导鱼雷齐射鱼雷捕获目标尾流概率大小的最主要因素。此时要特别注意目标航向误差，防止由于目标航向误差导致不满足鱼雷进入尾流角度要求。

表2 存在综合要素误差时鱼雷捕获目标尾流概率

2)在仿真条件下，当目标舷角60°～110°时，目标速度误差大小是影响尾流自导鱼雷齐射鱼雷捕获目标尾流概率大小的最主要因素。特别是若期望2雷能够同时捕获目标尾流时，条件允许的情况下，要首先修正目标速度误差或利用各种手段获取较为准确的目标速度。

3)为提高大误差条件下尾流自导鱼雷齐射鱼雷捕获目标尾流概率，应优先选择目标舷角70°～90°发射阵位。