基于RAIM的解决多星故障监测算法

张 宇，李岱若

(中国人民解放军92941部队44分队，辽宁 葫芦岛 125003)

随着现代全球卫星导航系统(GNSS)的发展，卫星定位与导航的精度得到明显提升，使得GNSS接收机的应用范围得到大面积扩展。此时，卫星导航系统的完好性成为了限制接收机使用的重要因素。接收机自主完好性监测(RAIM)作为完好性检测链路的末端，相比于其他方法，具有快速监测接收机本地误差的优点。传统RAIM方法大多基于单星故障假设，而伴随着GNSS可用卫星数显著增加，多颗卫星同时发生故障的概率也将增大。同时，在信号恶化场景下，如城市、峡谷、山区等，多星观测量很容易出现粗差。因此，需要研究分析针对多星故障的RAIM算法。为了尽量缩短报警时间和不影响接收机的采样频率，RAIM算法的执行应该相对简单。

目前多星RAIM算法的研究主要集中于最小二乘残差的一致性检验，但也有其他一些不同的检验方法。文献［1］详细分析了传统w-test迭代方法在多星故障检测时的缺陷。为减小计算量，改进算法在获得初始调整结果后只对检测统计量的相关性进行处理。文献［2］介绍并改进了三种用于城市环境下的多星故障RAIM方法。这三种方法分别为观测量子集方法、前向-后向方法和Danish方法。同时文中也指出了可分离度检验在避免剔除无故障星方面的重要性。文献［3］利用现代GNSS的高冗余度，每次迭代时识别两颗故障星，通过牺牲一些正确测量值来识别多星故障。当已知故障卫星数时，奇偶向量法可以用于多星故障检测，但其对矩阵操作较多导致计算量大［4-5］。利用不同历元的观测量或者引入约束条件，可以重构出被最小二乘完好性算法损失的误差向量［6-7］。文献［8］利用故障检测比故障排除简单的特征，首先获取初始无故障星座，再逐步搜索剩余卫星，实现故障排除。

本文结合前向-后向方法，使用改进的w-test算法，每次迭代识别两颗故障星。同时考虑观测量之间的相关性，进行可分离度检验。后向时，针对每颗被剔除卫星，只通过计算该星的残差而不是最小二乘估计来判断剔除是否正确，从而减小计算量。

1 传统w-test方法

由于伪距测量值与接收机位置等状态变量之间的非线性，需要围绕初始状态进行线性化。测量模型表达式为

式中，ΔY为观测伪距与预测伪距的之差;H为视线距离对状态向量的一阶导数;ΔX为状态向量偏移;ε 为观测误差向量。

式(1)的加权最小二乘解为

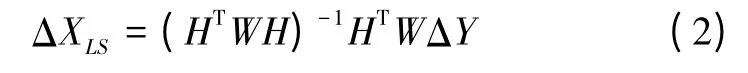
式中，W=(COV(ε))-1，为加权矩阵。在本文中W为单位矩阵。

由式(1)和式(2)可得最终的残差向量为

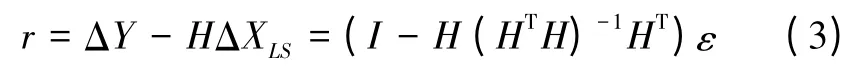
记S=(I -H(HTH)-1HT)。最小二乘完好性算法使用残差的平方和作为检测统计量，定义为

故障检测时，首先进行全局检测。假设无故障时观测误差为高斯白噪声，则SSE应服从自由度为(m -n)的χ2分布，其中，m为观测量个数，n为状态变量维数。将检测统计量与全局门限进行对比，若超过门限则表明残差不一致，有故障星存在。全局门限的表达式为

其中，PFA为虚警率，由具体应用要求确定。

若没有通过全局检测，则进行局部检测。此时，传统w-test方法使用每颗卫星的归一化残差作为检测统计量，表达式为

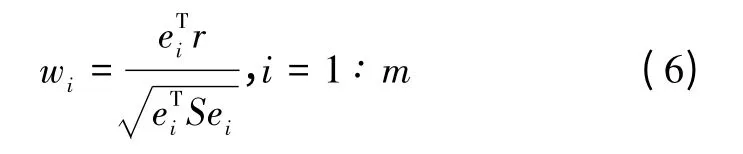
式中，ei是第i个元素等于1的单位矢量。假设无故障时，第i颗卫星观测噪声εi的方差为σ2，则wi应服从正太分布N(0，σ2)。将与局部门限进行对比，凡是超过门限的都为故障星。局部门限的表达式为

2 传统w-test方法的局限

传统w-test方法每次迭代只识别一颗故障星，这样使得当检测统计量存在相关性时，会造成漏检或误检。例如，假设两个统计量之间强相关，并且其中只有一个观测量有粗差。此时另一个统计量也有可能超过门限，从而被RAIM算法剔除，真正的故障星却被留下。最终经过反复迭代，最小二乘估计结果出现偏差，使得无法识别出真正的故障星，造成较大的定位误差。统计量之间的相关性与故障星的个数和故障幅值成正比［1］。

因此，为了在多星故障时使用w-test方法，可分离度检验的概念被提出［1］。可分离度检验计算每两颗卫星之间的相关系数，之后在故障识别时考虑相关系数［1-2，9］。两颗卫星之间相关系数的计算公式为

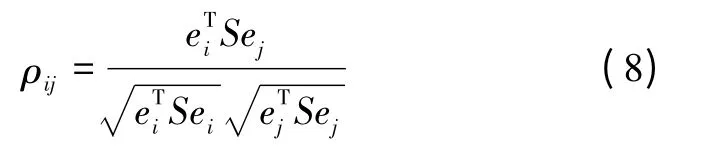
式中，ej是第j个元素等于1的单位矢量。

3 改进w-test方法

目前基于w-test方法的多星故障RAIM方法多集中于残差相关性的处理上，但每次仍然只识别一颗星。这样当残差相关时，第一次识别的结果有可能将正常星剔除，对后续迭代产生不利影响。为此，本文对传统w-test方法进行改进，并采用前向-后向方法，以尽可能恢复被错误剔除的正常星。

前向过程中，若全局检测没有通过，则局部检测时，改进w-test方法每次识别两颗故障星而不是一颗。对应第i颗和第j颗卫星的检测统计量为

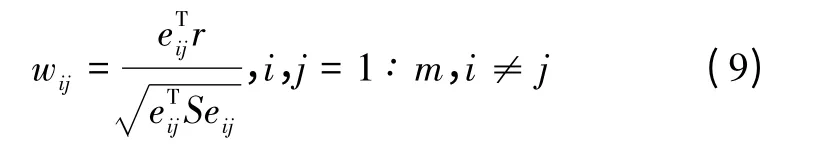
式中，eij是第i个和第j个元素等于1的矢量。

后向时，对每颗标记故障星进行回代，此时不再进行最小二乘估计，而只利用初步位置信息计算每颗标记故障星的伪距残差，以判断是否恢复该星为正常星。由于最小二乘估计中涉及矩阵操作，这种处理可使算法得以简化。卫星伪距残差的计算公式为

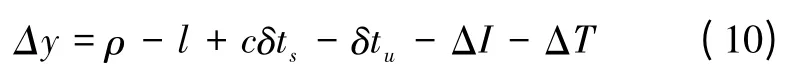
式中，Δy为伪距残差;ρ 为该星的伪距观测量;l为初步接收机位置与卫星位置之间的距离;δts和δtu分别为卫星钟差和接收机钟差;ΔI和ΔT分别为电离层延迟和对流层延迟。因此，对每颗故障星构造的残差向量为

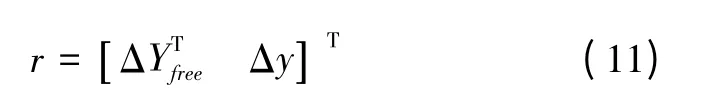
其中，ΔYfree为前向获得的初步无故障星残差向量。根据式(11)按式(4)计算检测统计量，进行全局检测。若小于全局门限，则将该星恢复为正常星，否则仍为故障星。对所有标记故障星进行恢复确认后，获取最终无故障星座，进行最小二乘估计，作为本次历元的最终导航结果［10］。改进RAIM方法的流程图如图1所示。

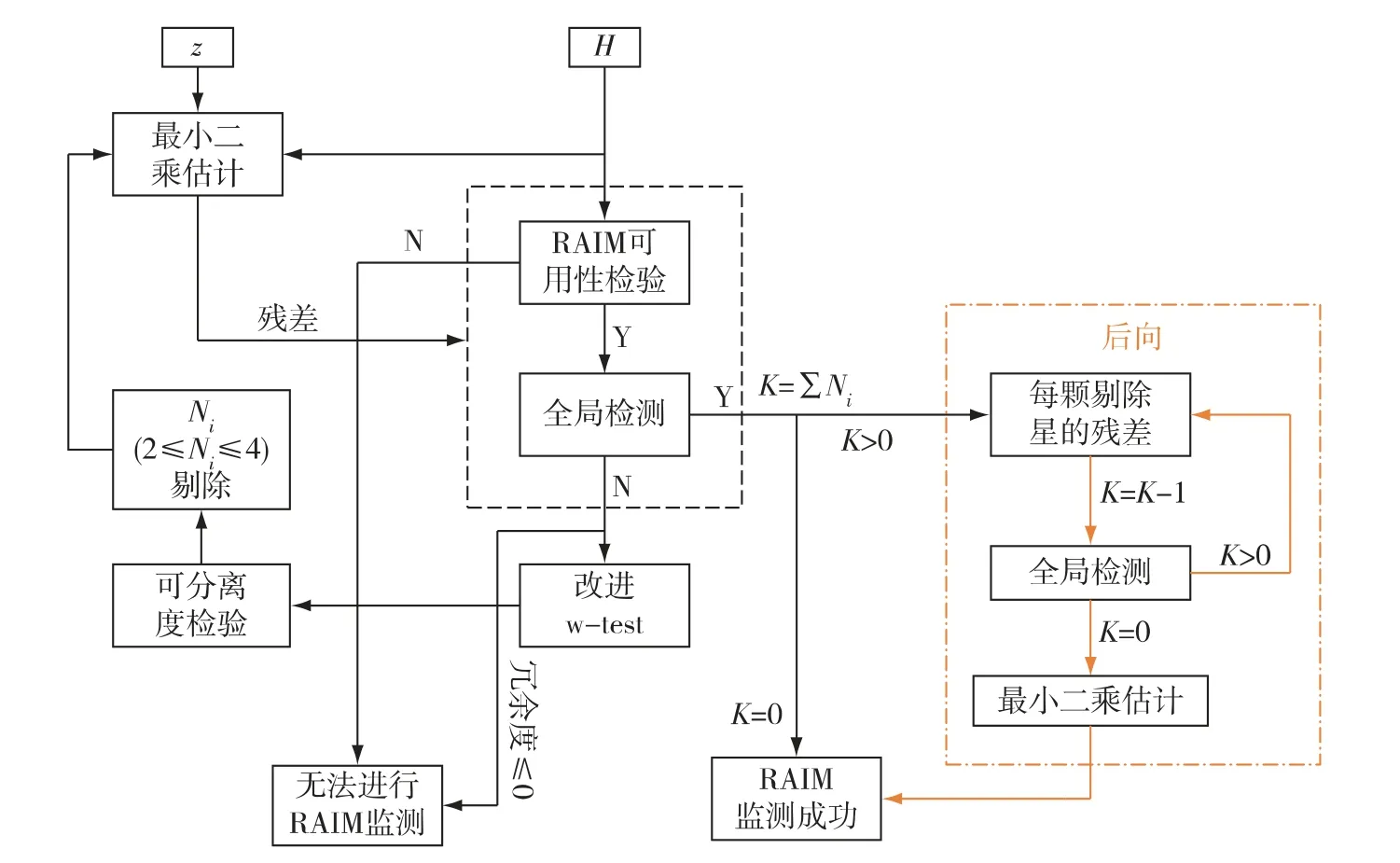
图1 改进多星故障RAIM方法流程图

改进算法的过程可以概括如下:

1)利用m个观测量进行最小二乘估计，并按式(9)计算检测统计量;

2)将最大统计量对应的两颗星标记为故障星;

3)按式(8)分别计算这两颗星与其他星的相关系数，若最大相关系数超过门限，则将对应星也标记为故障星。记本次迭代标记的故障星数为Ni(2≤Ni≤4);

4)将故障星从观测量中剔除;

5)重复1)～4)，直至通过全局检测，获得初始无故障星座和初步位置信息。记总迭代次数为t和初步无故障星数为OF，则OF=m -N1-N2-...-Nt;

6)按式(10)分别计算每颗故障星的残差，按式(11)和式(4)计算检测统计量，若通过全局检测，则该星恢复为正常星。记被恢复的星数为RE;

7)获得最终的无故障星座，共OF+RE个观测量。利用这些观测量进行最小二乘估计，作为最终的导航解算结果。

4 仿真分析

采用中国航天704所研制的双系统接收机(GPS L1和BDS B1)采集测量数据。使用该接收机进行长约45 min的静态测试。天线位于实验室楼顶。以事后处理的方式比对传统方法和改进方法的检测性能。

测试时间段内，可见卫星数如图2所示。

图2 可见卫星数目

为考察RAIM算法的适应性，在不同时刻对不同卫星的伪距加入误差，误差大小为60 m。具体仿真的故障场景如表1所示。

表1 不同的仿真场景

表1中，‘B’代表BDS，‘G’代表GPS，‘B’或‘G’后面为卫星号。单故障和双故障时，接收机的导航模式设置为BDS。7星故障时，单BDS无法识别，因此，导航模式设置为BDS+GPS。

单星故障时，传统方法第一次迭代即正确识别出故障星，说明传统方法适用于单星故障场景。改进方法的识别过程如表2所示，括号内的星为通过可分离度检验标记的故障星，‘0’代表没有与该故障星相关性较强的星。

由表2可知，在将正常星标记为故障星后，可分离度检验将与之相关性较强的真正故障星也标记为故障星。同时由表2可知，后向过程可以将前向错误标记的故障星恢复。

表2 单星故障时改进RAIM方法结果

双星故障时，传统方法的识别过程如表3所示。

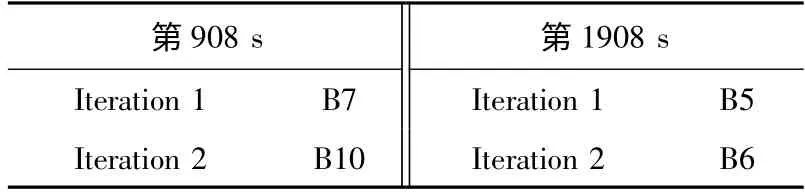
表3 双星故障时传统RAIM方法结果

由表3可知，由于传统w-test每次只识别一颗故障星，使得第一次即剔除错误。剔除正常星后，故障星的权重得到提高，进一步造成后续迭代识别错误。最终导航解算结果发生偏移，产生较大定位误差。

改进方法的识别过程如表4所示。

由表4可知，由于改进w-test方法每次识别两颗故障星，因此第一次迭代即正确识别出故障星。可分离度检验将与真正故障星相关性较强的正常星也标记为故障星，但后向时将其恢复。

7星故障时，传统方法的识别过程如表5所示。

表4 双星故障时改进RAIM方法结果

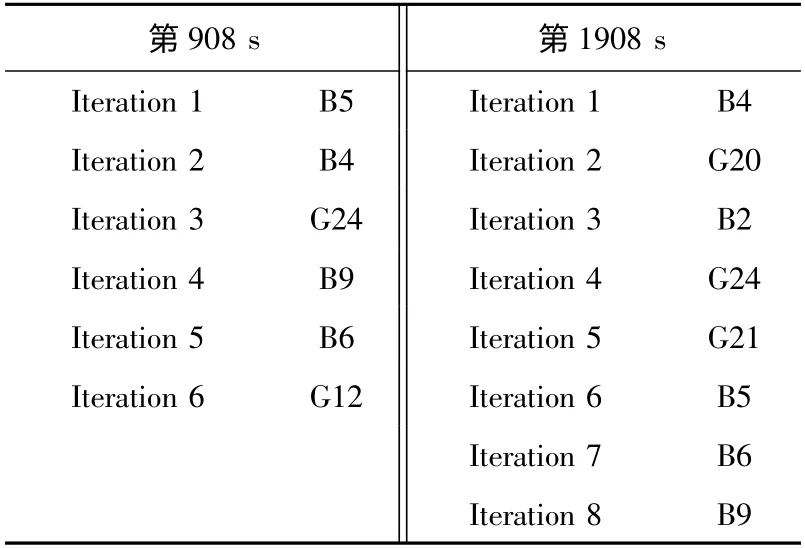
表5 7星故障时传统RAIM方法结果

由表5可知，第908 s时，传统方法正确识别出BDS故障星，而GPS则识别错误。第1908 s时，BDS和GPS都识别错误。

改进方法的识别过程如表6所示。

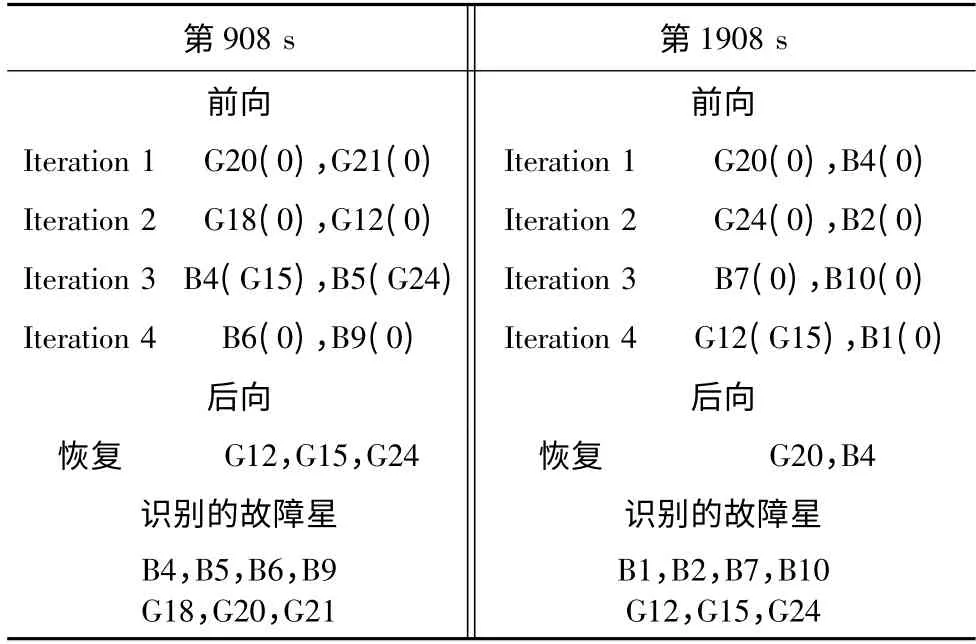
表6 7星故障时改进RAIM方法结果

由图2和表6可知，在可见星数为16和17颗时，改进方法能够正确识别7颗故障星。比较表5和表6可知，改进算法的迭代次数较传统算法有所减少。

2星和7星故障时，传统方法和改进方法的定位误差分别如图3和图4所示。

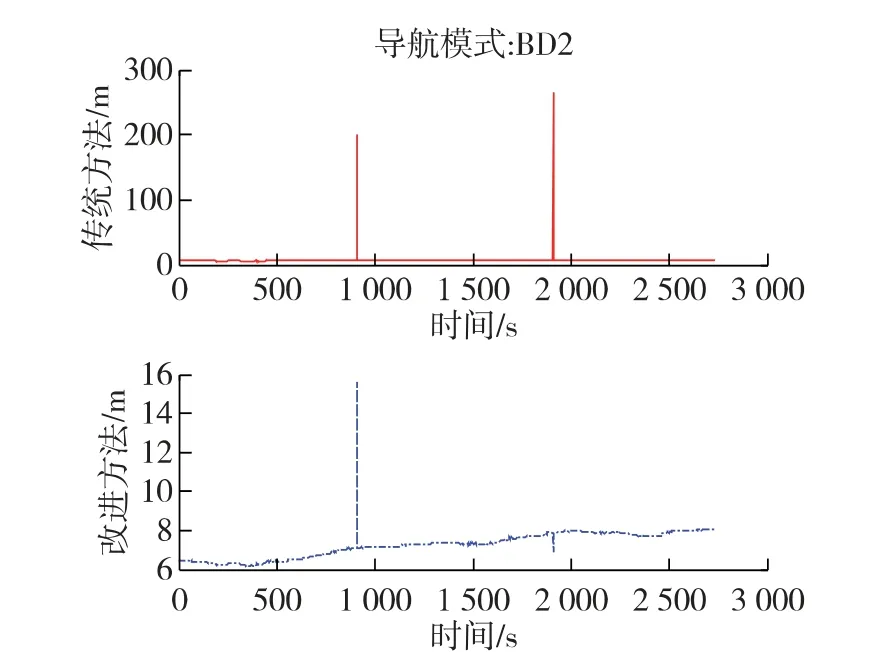
图3 双星故障时两种方法的定位误差

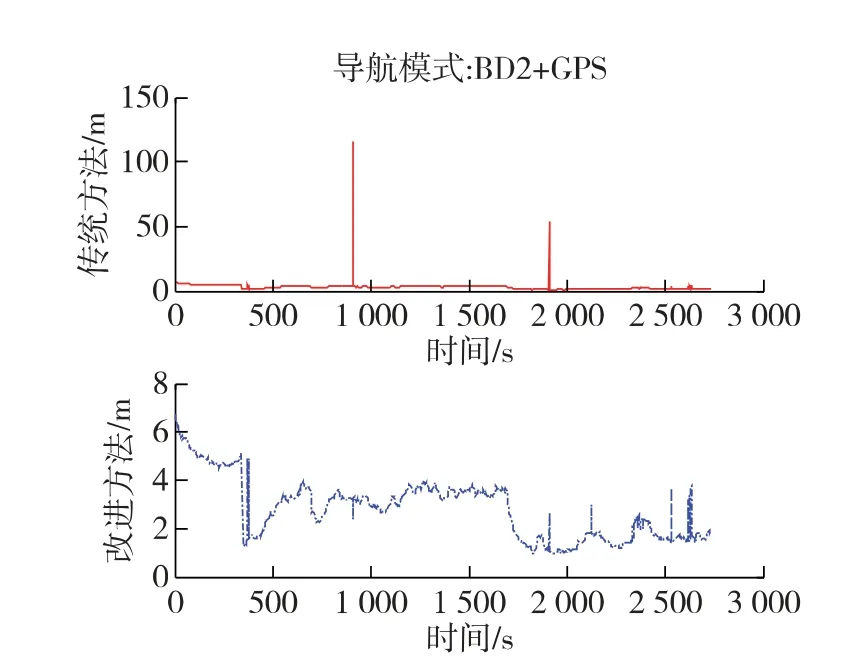
图4 七星故障时两种方法的定位误差

这两种场景下，传统方法将正常星剔除，留下故障星，造成较大的定位误差。而改进方法则能够正确识别出故障星，定位误差较小。由于剔除故障星后，参与定位的卫星数减少，因此故障时刻的定位误差稍大于其他时刻。

5 结束语

作为接收机必不可少的功能，RAIM算法的性能是影响接收机使用范围的重要因素。传统单星故障检测方法在多星故障时失效。本文对传统w-test方法进行改进，使其适用于多星故障。改进方法可一次识别两颗故障星，为避免统计量相关性强时造成漏检，也进行了可分离度检验。由于每次迭代最多识别4颗故障星，这种方法也可以加速前向的识别过程。后向时，只计算每颗故障星的残差而不进行最小二乘估计，进一步减小了计算量。仿真试验表明，改进方法能够有效识别出单星故障和多星故障，提高了故障识别的可靠性及识别效率。

当故障星使导航结果发生严重偏移时，可使正常星的残差统计量表现为粗差。剔除这些正常星后则残差一致性较好。这种情况下所有基于残差一致性和全局检测的RAIM算法都将失效。将来工作将研究这种现象产生的机理以及解决方法。