直升机后缘襟翼驱动器迟滞现象仿真与抑制

周金龙，董凌华，杨卫东

南京航空航天大学 航空学院，直升机旋翼动力学国家级重点实验室，南京 210016

主动控制后缘襟翼(Actively Controlled Flap,ACF)是一种行之有效的直升机旋翼振动主动控制技术[1-3]。安装在直升机桨叶后缘的襟翼在驱动器作用下动态偏转，产生附加的气动载荷，从而抵消部分旋翼振动载荷。整个后缘襟翼旋翼系统由基体桨叶、后缘襟翼以及附属的驱动器组成，结构简单紧凑，并且因为后缘襟翼的驱动机构位于旋翼上，与直升机操纵线系无直接联系，后缘襟翼机构失效不会危及直升机飞行安全，相比其他形式的旋翼振动主动控制技术，如高阶谐波控制[4](Higher Harmonic Control,HHC)和独立桨叶控制[5-7](Individual Blade Control,IBC)，主动控制后缘襟翼可靠性更高，在当前技术条件下更具工程应用潜力。

由于后缘襟翼安装在旋翼桨叶上并与之同步旋转，同时承受气动载荷和离心载荷的作用，并且需要在控制信号作用下作高频偏转，要求后缘襟翼驱动器在具有足够的力和位移输出性能的同时具有较宽的工作带宽，给后缘襟翼驱动器的选择和设计带来挑战。压电材料具有输出力大、工作频率高的优点，因此现有的主动控制后缘襟翼旋翼方案多选择带有位移放大机构的压电叠堆驱动器作为后缘襟翼的驱动元件[8-13]。但是压电材料固有的迟滞特性使得期望襟翼偏角与实际襟翼偏角之间存在一定偏差，使襟翼偏转运动与襟翼控制信号之间存在延迟。Viswamurthy等[14-16]使用经典的Preisach模型对压电驱动器进行建模，并首先开展了驱动器迟滞对后缘襟翼振动控制性能影响分析，仿真结果显示忽略驱动器迟滞效应将会对后缘襟翼最优控制率的预测带来较大误差，甚至可能会增大旋翼振动载荷。Mallick等[17]使用椭圆曲线对压电驱动器进行建模，并研究了压电驱动器非线性迟滞对振动控制效果的影响，研究结果显示迟滞会在一定程度上降低后缘襟翼振动控制效果。Muir等[18-19]通过实验研究了压电驱动器动态迟滞特性，并采用经典Preisach模型研究了迟滞对大速度前飞状态下后缘襟翼振动控制和噪声抑制性能的影响，发现迟滞对开环状态下噪声控制性能影响明显，但是对闭环状态下振动和噪声控制影响有限。

压电驱动器的迟滞特性与压电材料特性、驱动器结构等因素相关，不同压电驱动器迟滞特性存在差异，对后缘襟翼旋翼振动控制性能的影响也不完全相同；并且压电驱动器迟滞受驱动信号频率的影响，经典的Preisach迟滞模型不具有率相关特性，难以模拟不同驱动频率下后缘襟翼运动规律[20]；同时已开展的研究多集中在驱动器迟滞对振动噪声抑制性能的影响方面，而较少有对后缘襟翼驱动器迟滞抑制的研究。Viswamurthy和Ganguli[16]采用经典Preisach模型的逆模型开展了驱动器迟滞补偿仿真研究，经典Preisach模型计算量较大，并且由于经典Preisach模型的率不相关特性，难以精准模拟后缘襟翼多频率控制输入下襟翼偏转运动迟滞现象。此外后缘襟翼偏角受襟翼离心载荷与驱动器迟滞影响，其中离心载荷对襟翼偏角影响是不可消除的，其影响大小取决于襟翼质量分布以及旋翼工作转速，可以通过合理优化设计后缘襟翼结构、降低襟翼质量、减小襟翼铰链摩擦等方式降低离心力对后缘襟翼偏转角度的影响，而驱动器迟滞主要是由驱动器自身特性决定的，因此采用Bouc-Wen模型对应用于后缘襟翼旋翼的压电驱动器进行了建模，并与带后缘襟翼的旋翼动力学模型相结合，研究了压电驱动器迟滞对主动控制后缘襟翼旋翼振动控制性能的影响；针对该驱动器的迟滞特性，建立了基于Bouc-Wen逆模型的前馈控制与PID反馈控制相结合的控制策略，显著地抑制了该驱动器非线性迟滞，为后续的后缘襟翼旋翼设计与振动控制实验奠定了基础。

1 驱动器迟滞建模

由于压电材料输出位移较小，在实际应用时需要配合适当的位移放大机构，常见的位移放大机构如X型放大机构[8-9]、L型放大机构[11-12]以及菱形放大机构[10,13]等，由于菱形放大机构结构简单，并且不存在机械间隙的影响，因此后缘襟翼多采用带有菱形框或类似结构的放大机构的压电叠堆驱动器。根据后缘襟翼旋翼需求研制的带有菱形框放大机构的压电叠堆驱动器如图1所示。

该压电驱动器安装到后缘襟翼桨叶上，其固定端与旋翼桨叶固定安装在一起，输出端与后缘襟翼相连，并通过铰链机构将驱动器输出端的直线位移输出转换为后缘襟翼的偏转运动。驱动器在一端固定一端自由的状态下工作性能参数如表1 所示。

为研究该压电驱动器迟滞现象，设置偏置电压为40 V、幅值(零-峰值)为40 V的正弦驱动电压，不同驱动频率下该压电驱动器迟滞如图2所示。

图1 压电驱动器与后缘襟翼桨叶

表1 压电驱动器参数

从图2可以发现，该压电驱动器驱动电压与输出位移之间存在明显迟滞现象，并且随着驱动频率的提高，驱动器的迟滞逐渐增加，因此有必要对该驱动器迟滞特性进行建模分析，并研究其对后缘襟翼旋翼振动控制性能的影响。

常用的压电材料迟滞模型有Preisach模型、KP(Krasnosel’skii-Pokrovskii)模型和PI(Prandtl-Ishlinskii)模型等，这些模型能够较为准确地描述压电材料的迟滞现象，但是由于其模型运算复杂，难以应用于实时控制系统。Bouc-Wen模型具有参数少、计算效率高的特点，因此本文采用Bouc-Wen模型[21-23]对应用于后缘襟翼的压电驱动器进行迟滞建模。Bouc-Wen模型通过引入状态变量h来描述系统的迟滞现象：

(1)

式中：迟滞曲线形状受α、β和γ控制；u为施加到压电堆上的电压；d为驱动器有效逆压电系数；n为模型的阶数，为了降低模型的计算量，取n=1，式(1)简化为

(2)

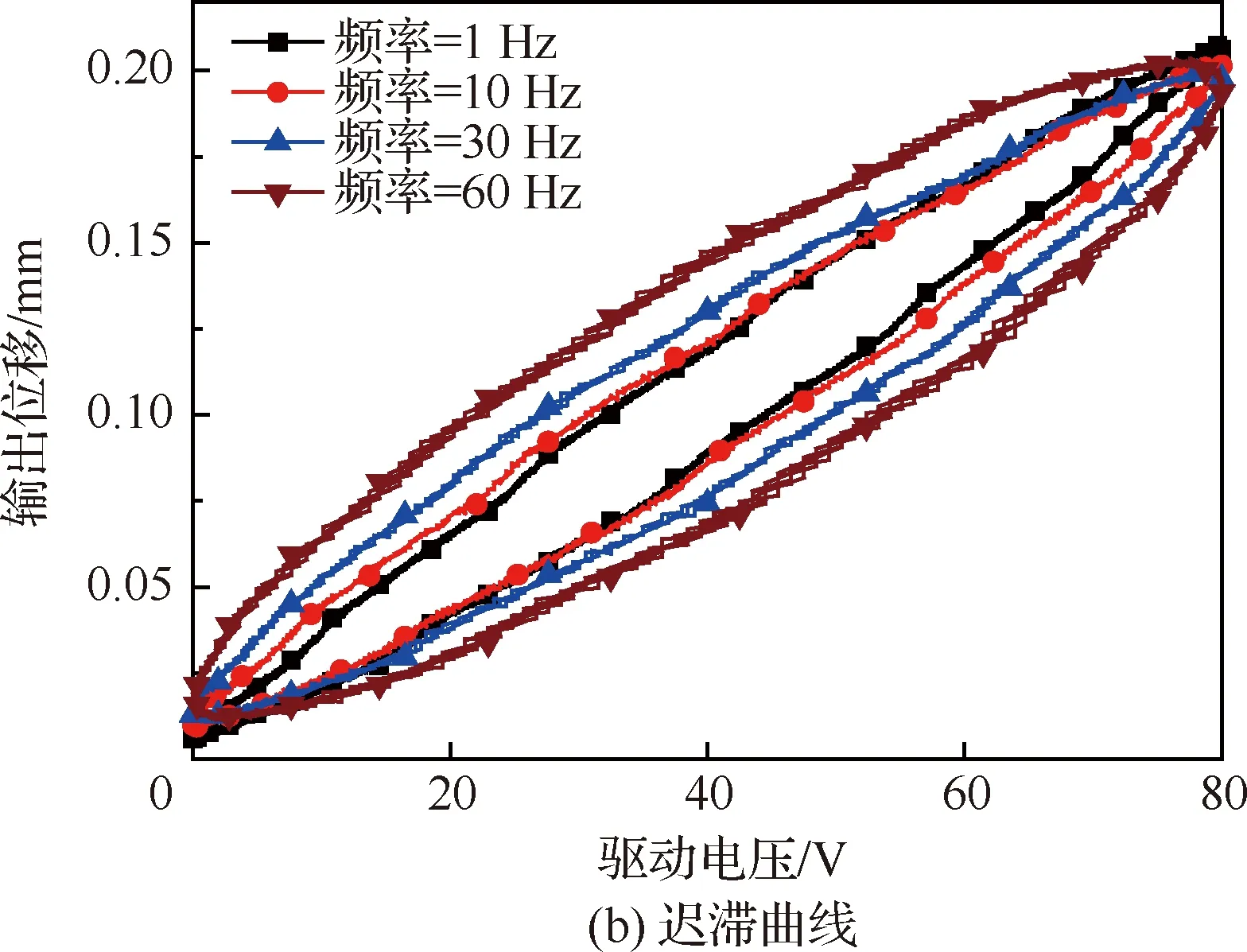
图2 不同频率下迟滞现象

在旋翼旋转时，后缘襟翼会在气动载荷作用下而发生被动偏转，进而降低后缘襟翼的控制功效。为了减小后缘襟翼的被动偏转幅度，需要驱动器具有较大的刚度特性。同时由于驱动器需要带动后缘襟翼动态偏转，其质量和阻尼特性也会影响其工作性能。考虑质量、阻尼和刚度特性的包括位移放大机构的压电驱动器运动方程可表示为

(3)

式中:m为压电驱动器的有效质量;b为压电驱动器阻尼;k为压电驱动器刚度;x为驱动器输出位移。包含位移放大机构的压电驱动器Bouc-Wen模型如图3所示。

在不考虑驱动器高阶模态前提下，包含位移放大机构的整个驱动器动态特性可采用二阶系统传递函数来描述。包含位移放大机构的压电驱动器刚度k可以通过实验测量的方式获得。通过扫频实验获得驱动器一阶共振频率fr后，根据系统固有频率与质量、刚度之间的关系：

(4)

从而有：

(5)

包含位移放大机构的压电驱动器输入输出特性主要由压电叠堆的非线性迟滞和整个驱动器的动态特性决定，在低频驱动电压作用下，不同频率下压电驱动器迟滞曲线几乎完全重合(图4)，可以认为该驱动器在静态或较低频率下的迟滞现象主要由压电材料自身迟滞特性决定，与整个驱动机构的动态特性无关，因此Bouc-Wen模型的辨识过程可以分为2步：①根据低频驱动电压下实验测量迟滞数据辨识与压电材料迟滞相关的模型参数；②在此基础上根据较高频率驱动电压下实验测量迟滞参数辨识与驱动机构动态特性相关参数。分步辨识减少了每次辨识过程中待辨识参数个数，提高了辨识精度和效率。

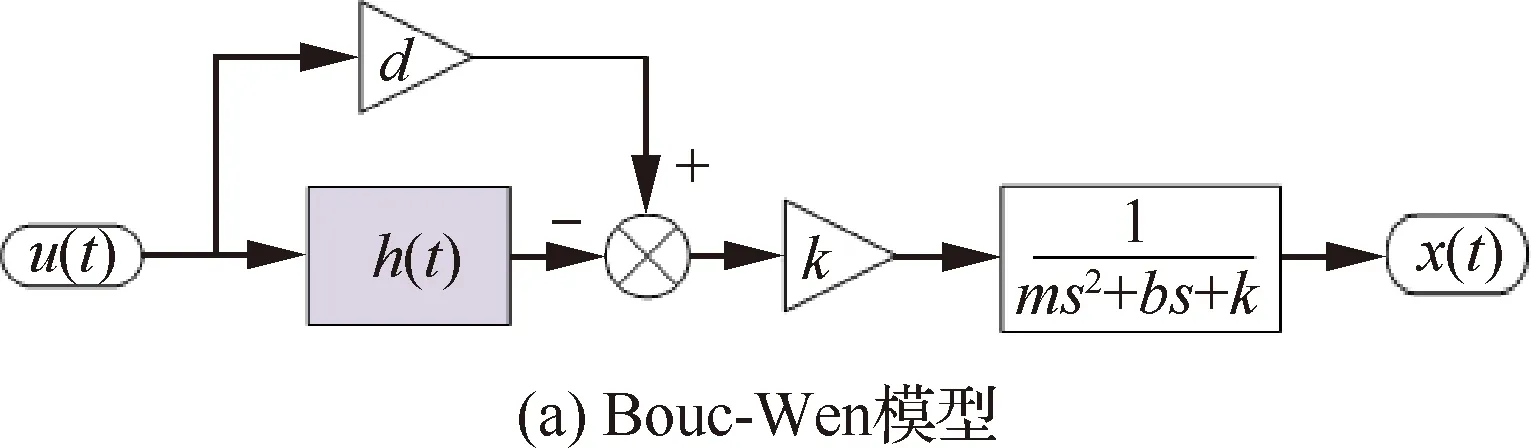
图3 Bouc-Wen模型框图

在低频驱动电压作用下，忽略整个驱动机构质量、阻尼和刚度对系统输入输出特性的影响，式(3)可以简化为

x=du-h

(6)

此时Bouc-Wen迟滞模型有d、α、β和γ共4个未知参数。粒子群算法(Particle Swarm Optimization, PSO)具有搜索速度快、需调整参数少以及结构简单的优点，因此本文采用粒子群算法辨识Bouc-Wen模型中的未知参数，建立适应度函数为

(7)

低频下PSO辨识效果如图6所示，结果显示PSO辨识效果良好，建立的Bouc-Wen模型能够较好地反映低频下压电驱动器迟滞现象。

以同样的方式辨识高频信号作用下驱动器迟滞参数，保持d、α、β和γ的值不变，此时式(3)表示的Bouc-Wen模型仅含有线性阻尼b一个未知参数。PSO辨识得到的Bouc-Wen模型参数如表2所示。10～60 Hz驱动电压作用下Bouc-Wen模型输出与实验测量结果对比如图7所示，从图中可以看出，本文建立的Bouc-Wen模型能够在较宽的频率范围内准确地描述带有菱形放大机构的压电驱动器迟滞现象。

图4 低频迟滞

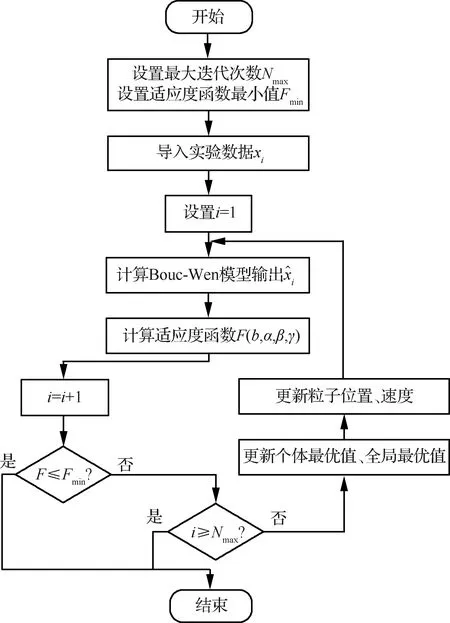
图5 粒子群算法辨识流程

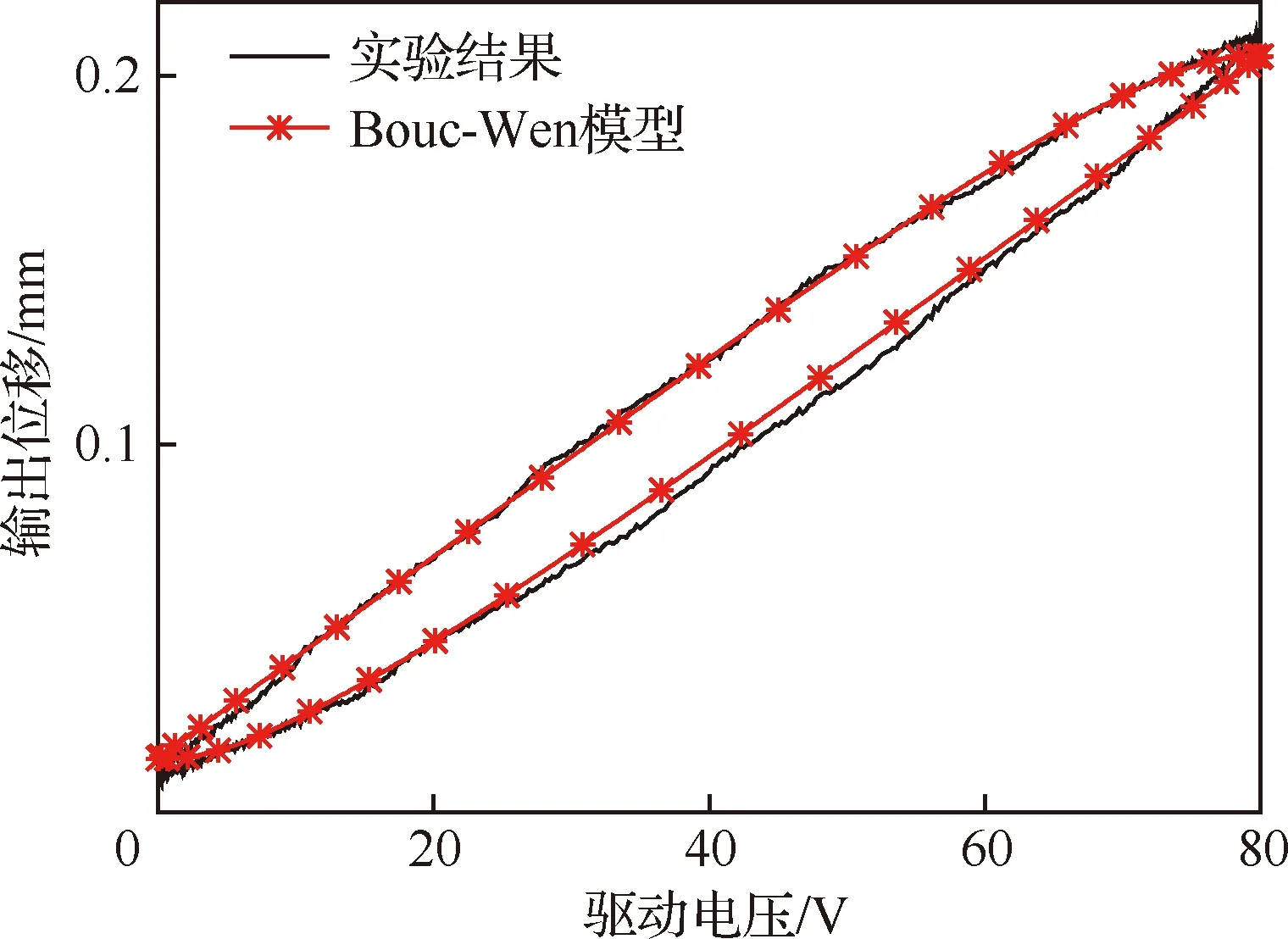
图6 实验结果与模型输出比较(1 Hz)

表2 Bouc-Wen模型参数

图7 不同频率下模型输出与实验结果比较

2 迟滞抑制

为了抑制压电驱动器的迟滞现象，开展了基于Bouc-Wen逆模型的前馈控制研究。根据Bouc-Wen模型输入电压与输出位移关系可得：

(8)

根据式(8)建立基于Bouc-Wen逆模型的前馈补偿控制系统如图8所示。以10 Hz前馈补偿控制实验效果为例(图9)，从图中可以看出，压电驱动器迟滞现象都得到了显著的抑制，但是迟滞现象并没有被完全消除，驱动器位移输出与期望位移之间存在一定偏差。

图8 前馈补偿

通过采用基于Bouc-Wen逆模型的前馈补偿消除大部分的驱动器迟滞，然后使用PID控制来抑制由于建模误差而残余的迟滞，同时抑制由于外界扰动而引起的驱动器输出位移与期望位移之间的误差，从而提高驱动器输出位移精度，采用复合控制后驱动器输出位移与期望位移之间的偏差如图12所示，从图中可以看出，通过采用复合控制，驱动器位移输出偏差进一步减小，整体误差控制在5 μm以内。压电驱动器复合控制效果如图13所示，在10～60 Hz频率范围内，迟滞现象得到明显抑制，实验效果显示所建立的复合控制策略具有良好的适应性，能够应用于不同频率工作的后缘襟翼旋翼。

图9 前馈控制结果(10 Hz)

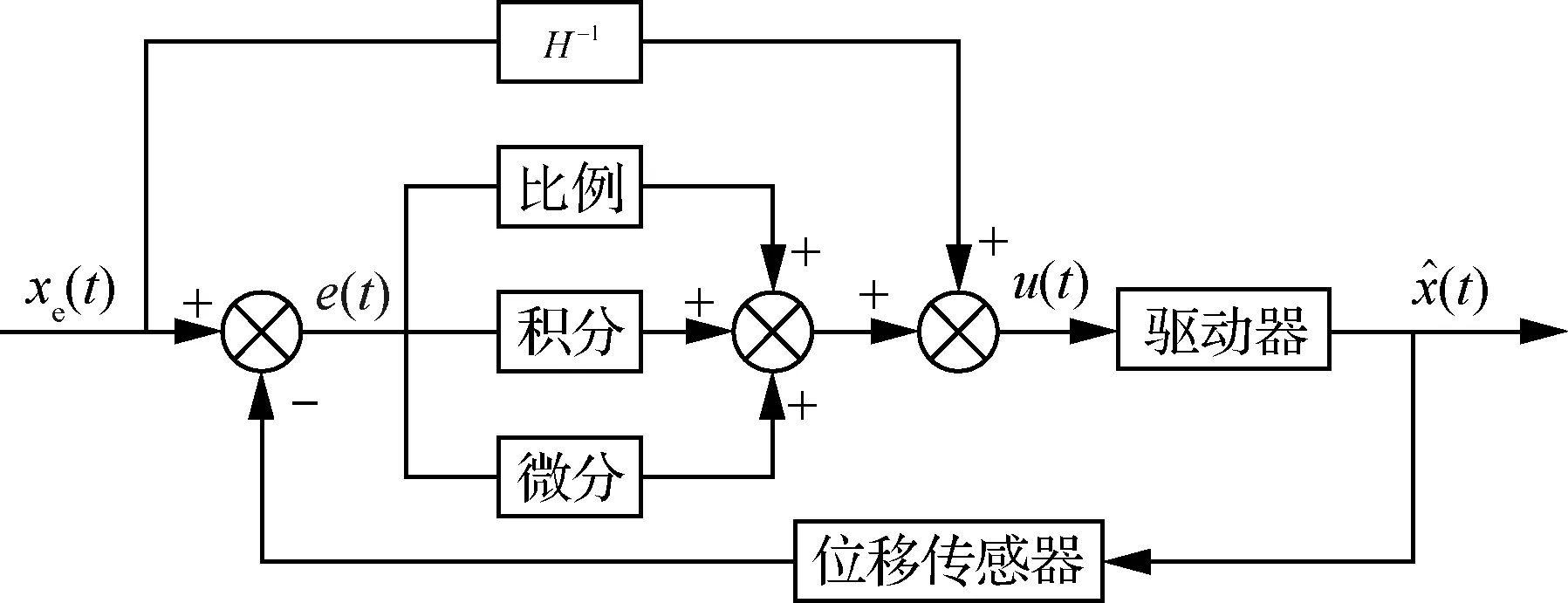
图10 复合控制结构

图11 实验装置

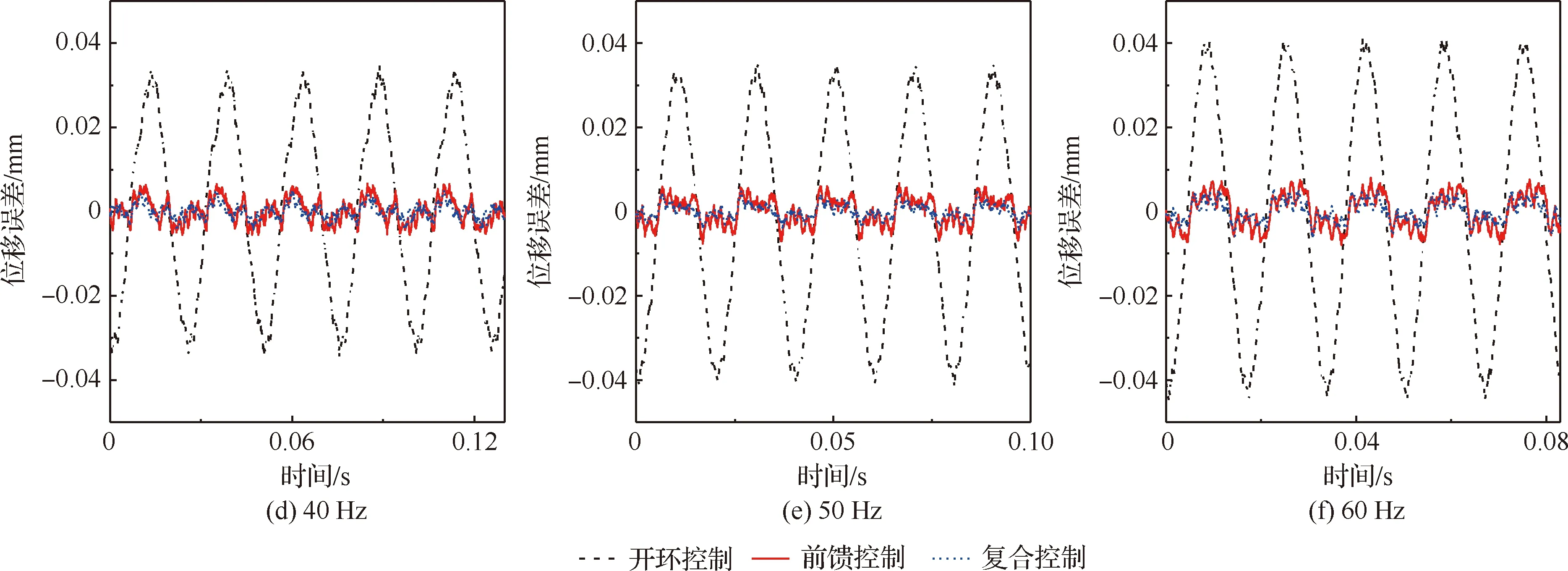
图12 位移误差

图13 复合控制效果

3 驱动器迟滞对振动控制性能影响

为了研究驱动器迟滞现象对直升机后缘襟翼振动控制性能的影响，建立了考虑驱动器迟滞的直升机后缘襟翼气弹耦合动力学模型，驱动器有/无迟滞状态下的振动载荷计算如图14所示。其中δf(t)为无迟滞的理想驱动器状态下的后缘襟翼偏角；δ′f(t)为有迟滞驱动器状态下的后缘襟翼偏角；z为旋翼桨毂振动载荷谐波系数向量。

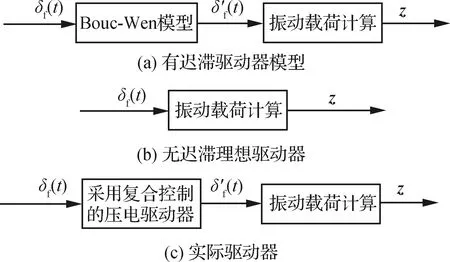
图14 驱动器有/无迟滞状态下振动载荷计算

建模对象压电驱动器满足后缘襟翼旋翼驱动需求，并且在测试中表现出迟滞现象，因此以该驱动器迟滞特性为基础建立考虑驱动器迟滞的旋翼动力学模型。在无迟滞理想驱动器情况下优化得到的后缘襟翼偏转角度转换成位移信号后激励压电驱动器，并采用复合控制抑制其迟滞现象，再将测量得到的驱动器位移输出转换为偏角后输入到载荷计算模块中，以半实物仿真的方式研究复合控制策略对后缘襟翼振动控制性能的影响。

考虑到后缘襟翼旋翼各个部件之间作用比较复杂，难以直接使用牛顿定律建立其运动方程，因此采用Hamilton原理建立包含后缘襟翼、旋翼在内的动力学方程：

(9)

式中：δU为系统的虚位能；δT为系统的虚动能；δW为后缘襟翼旋翼在旋转过程中受到的外载荷虚功。所建立的旋翼动力学模型主要包括基体桨叶和后缘襟翼2部分，因此式(7)中的虚位能、虚动能和外载荷做功为桨叶和后缘襟翼两部分叠加而成：

(10)

(11)

(12)

式中：bi代表第i片桨叶；fi代表安装在第i片桨叶上的后缘襟翼，整个旋翼系统共有Nb片桨叶。

基体桨叶气动载荷采用查表法计算，根据所在翼型剖面处气流速度与迎角，查询对应翼型的气动力系数表，通过插值的方式获取相应的气动载荷系数，而安装有后缘襟翼的剖面处气动载荷采用准定常Theodorsen带襟翼翼型气动模型计算。具体的旋翼动力学建模过程详见文献[24-25]，分别取前进比为μ=0.053和μ=0.140下旋翼动力学模型计算结果与SA-349直升机飞行实测结果对比[26](图15)，结果显示所采用的旋翼动力学模型具有较高的计算精度，适合开展带后缘襟翼旋翼振动载荷计算。

本文采用离散时间高阶谐波控制(Discrete-Time Higher Harmonic Control, DTHHC)算法开展后缘襟翼振动控制仿真，在稳态前飞条件下直升机后缘襟翼旋翼系统可视为周期时不变系统，后缘襟翼控制输入与旋翼桨毂振动载荷响应满足：

z=Tθ+z0

(13)

式中:θ为后缘襟翼控制输入谐波(后缘襟翼偏角δf(t)或δ′f(t)经傅里叶级数展开后获得);z0为后缘襟翼保持静止时桨毂振动载荷谐波;T为系统传递矩阵，采用最小二乘法辨识T矩阵，辨识过程详见文献[25]。在考虑驱动器迟滞情况下辨识T矩阵时，后缘襟翼偏角信号在通过Bouc-Wen模型后再传递到载荷计算模块，而在无迟滞理想驱动器情况下，后缘襟翼偏角信号直接传递到载荷计算模块。由于驱动器迟滞的影响，在有/无驱动器迟滞情况下辨识得到的T矩阵发生了变化，相应的后缘襟翼最优控制率也将发生变化。

图15 模型计算结果与飞行实测数据

建立振动控制目标函数：

J=zTQz+θTRθ

(14)

式中：Q和R分别为旋翼桨毂振动载荷输出和后缘襟翼控制输入权重矩阵。因为后缘襟翼偏转角度受驱动器以及襟翼机构机械限制，并且襟翼的主动偏转运动需要消耗能量，因此通过合理调整Q和R可以在振动控制效果和襟翼控制输入间权衡取舍，以期达到综合最优的控制效果。为了比较在驱动器有/无迟滞下后缘襟翼振动控制效果，在仿真过程中，矩阵Q和R均设置为单位矩阵。

当目标函数取极值时有

(15)

代入式(11)和式(12),整理得到后缘襟翼最优控制谐波：

θopt=(TTQT+R)-1TTQ(Tθ0-z0)

(16)

本文选取中等速度稳态前飞状态开展仿真计算，旋翼桨叶和后缘襟翼参数如表3所示。考虑驱动器迟滞、不考虑驱动器迟滞以及采用复合控制的半实物仿真下后缘襟翼振动控制效果如图16所示，Fx、Fy和Fz分别为x、y、z方向分力；Mx、My、Mz分别为x、y、z方向力矩。半实物仿真中期望襟翼偏角与复合控制开/关时襟翼偏角如图17所示。

从图16可以看出，在当前仿真计算飞行状态下，驱动器迟滞会对后缘襟翼振动控制性能产生一定影响。虽然在驱动器无迟滞和有迟滞情况下后缘襟翼均具有良好的振动控制效果，但是相比于理想驱动器驱动下的旋翼振动载荷幅值，驱动器迟滞分别使Fx、Fy和Fz振动载荷幅值增大8.9%、7.9%和25.9%，Mx和My分别减小2.5%、3.7%，而Mz增大0.4%。虽然驱动器迟滞使Mx和My振动载荷幅值有所减小，却使得其他振动载荷分量产生更大程度的增加，在一定程度上使得后缘襟翼的综合减振性能有所降低。从图16和图17的半实物仿真结果可以看出，针对当前所采用的压电驱动器，复合控制能够有效地抑制驱动器迟滞对后缘襟翼偏角的影响，提高后缘襟翼振动控制性能。受桨叶内部的驱动器安装尺寸限制，驱动器输出功率有限，进而限制了后缘襟翼的偏角范围，在不改变已有的后缘襟翼驱动器的基础上能够尽可能充分利用驱动器有限的输出功率，提高振动控制效果，对于后缘襟翼研究是有意义的。

表3 旋翼与后缘襟翼参数

图16 考虑与不考虑迟滞情况下的振动控制效果

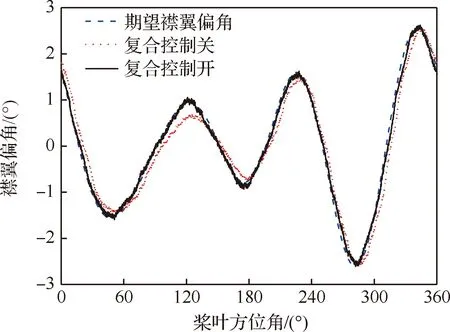
图17 襟翼偏角

4 结 论

针对带菱形位移放大机构的压电驱动器，通过实验研究了其在动态驱动电压下的迟滞现象；采用Bouc-Wen模型对该压电驱动器迟滞进行了建模，并将迟滞模型与旋翼动力学模型相结合，研究了迟滞对后缘襟翼振动控制性能的影响；为提高后缘襟翼振动控制性能，开展了驱动器迟滞抑制研究，建立了基于Bouc-Wen逆模型的前馈控制与PID反馈控制的复合控制策略，得到如下结论：

1) 压电驱动器在动态驱动电压作用下表现出的迟滞现象具有明显的率相关特性，随着驱动信号频率的升高，迟滞现象更加显著，仿真研究表明在中等速度稳态前飞状态下，驱动器迟滞会影响后缘襟翼振动控制效果。

2) 粒子群算法能够有效辨识Bouc-Wen模型参数，建立的Bouc-Wen模型能够在较宽的频率范围内较为精确地描述该压电驱动器的迟滞现象。

3) 采用基于Bouc-Wen逆模型的前馈控制与PID反馈控制的复合控制策略能够显著地抑制该压电驱动器的迟滞现象，驱动器位移输出误差控制在5 μm内，并且该控制策略在10～60 Hz频率范围内具有良好的适应性。