吸气式高超声速飞行器俯仰/滚转耦合运动特性
2020-06-08丛戎飞叶友达赵忠良
丛戎飞,叶友达,赵忠良
1. 中国空气动力研究与发展中心 高速空气动力研究所,绵阳 621000
2. 中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000
3. 国家计算流体力学实验室,北京 100083
2004年X-43A实验飞行器的成功试飞标志着吸气式高超声速飞行器已经从实验室阶段走向工程研制阶段[1-4]。2013年,美国洛克希德·马丁公司宣布正在研制代号为“黑燕”的SR-72高超声速无人侦察机作为SR-71的继承机型[5]。目前以美俄为代表的世界军事强国正在积极推动吸气式高超声速飞行器在军事领域的应用。
由于高超声速飞行器的飞行环境以及机体构型与传统飞行器不同,在稳定性研究中面临着很多新的问题。高超声速飞行器进行机动运动时,其气动特性通常是非线性、非定常变化的,并存在气动/运动耦合以及惯性耦合作用。由于高超声速飞行器通常采用细长体构型,其绕体轴X方向的转动惯量Ix通常较小,且高空高速飞行中的气动阻尼较小,使得飞行器在受到扰动时容易发生非指令性滚转[6-7]。
X-43A在2001年首次试飞时,在机弹分离后出现了滚转振荡发散现象,过大的载荷导致气动舵失效,从而导致试飞失败。研究人员分析认为是动力学耦合造成飞行器失稳,并将问题指向了气动模型的不可靠性[8]。在2010年4月和2011年8月,美国两次进行HTV-2的飞行试验,均以失败告终。其中第1次试飞失败是由于在飞行器爬升阶段发生滚转与侧滑交叉耦合,从而引起滚转发散,超过飞行器的滚转控制极限,最终导致飞行器失控[9]。由此可见,高超声速飞行器的动稳定性问题十分突出,给飞行器的运动稳定性和飞行安全带来了严峻的挑战[10-11],因此高超声速飞行器横侧向稳定性及其动力学耦合是必须研究的课题。
国内外针对传统飞行器的动稳定性开展的研究较早。Phillips[12]在研究XS-1模型时发现了由飞行器滚转引起的惯性耦合现象,从而提出了用于研究急滚动力学的Phillips判据。20世纪70年代,Mehra和Carroll[13]将分叉分析方法应用于飞行器稳定性分析,并指出机翼摇滚是由Hopf分叉引起的。Kandil[14]和刘伟[15]等分别开展了机翼单自由度滚动的非线性动力学分析研究,杨小亮[16]开展了后掠三角翼强迫俯仰、自由滚转耦合运动特性研究,张涵信等[17]针对球冠倒锥外形返回舱在跨、超声速配平攻角区出现极限环振荡的现象,提出了动稳定性判据及实现分叉的条件和分叉临界马赫数。袁先旭等采用耦合求解非定常Navier-Stokes方程和飞行器运动方程,数值模拟了飞船返回舱俯仰振荡随来流马赫数变化的Hopf分叉过程,验证了分析结论[18]。
针对高超声速飞行器的动稳定性研究则起步较晚,作者团队[10-11]在张涵信已发展的正滚判则的基础上,研究了类HTV-2高超飞行器的单自由度滚转以及强迫俯仰/滚转运动,完善了飞行器偏滚运动的稳定性判则,并指出高超声速飞行器高空飞行时,由于大气的密度低,飞行器自身的惯性力矩不能被忽略,惯性力矩会迅速加快滚动速度,诱导偏离振荡及惯性耦合发散。李乾等[19-20]对类HTV-2高超飞行器在两自由度耦合运动条件下的气动/运动耦合现象进行了研究,发现飞行器在俯仰机动过程中,滚转方向会在气动力矩以及惯性力矩共同作用下发生失稳运动。
目前针对吸气式高超声速飞行器动态特性开展的研究较少,以单自由度动稳定性研究为主,较少涉及多自由度耦合运动研究。Adamczak和Bolender[21]对HIFiRE-6一体化飞行器的纵向以及横航向运动模态进行了分析,指出飞行器在小迎角下横侧向通道动不稳定。刘绪等[22-23]等通过数值模拟针对类X-51机体/推进一体化飞行器在给出了进气道堵塞和通流两种外形下小振幅强迫振动的俯仰、偏航、滚转阻尼导数和交叉导数,并对两种外形下的计算结果进行了分析。赵忠良等[24-25]在0.5 m高超声速风洞针对类X-51A外形的带进气道通流模型进行了动导数试验,研究了模型进气道喉道高度对吸气式高超声速飞行器动导数的影响。
对吸气式飞行器而言,由于机体外形以及气动特性与滑翔式飞行器有较大区别,其动稳定性值得进行进一步的研究。本文针对一种类似SR-72构型的吸气式高超声速飞机开展了动稳定性研究。通过数值模拟获得了滚转单自由度动稳定性以及强迫俯仰/自由滚转运动下的两自由度耦合动稳定性。
1 数值方法和计算模型
本文的数值模拟研究在课题组研发的软件VFNS[26]上完成,该软件采用并行结构网格求解器,求解非定常Navier-Stokes方程,采用高阶Adams预估校正法在双时间步内实现空气动力/飞行力学的紧耦合计算,控制方程空间离散采用的是基于多块拼接网格的有限体积法,黏性项采用中心差分,无黏项采用Van Leer格式,非定常时间推进采用双时间步法,湍流模型为Spalart-Allmaras模型。
本文研究的吸气式高超声速飞行器模型是参照美国SR-72[27-28]概念飞行器设计的,采用了翼身组合体气动布局,与HTV-2和X-51A等高超声速飞行器普遍采用的“乘波体”构型有较大的不同。图1和图2分别给出了模型几何外形以及内流道形状。计算网格拓扑如图3所示。
为了模拟吸气式高超声速飞行器典型的巡航状态,计算工况选取为高度为27 km的标准大气参数,马赫数Ma=6。计算参考长度为模型全长,参考面积为机翼面积,力矩参考点为1/2全长的位置。以模型全长为参考长度的雷诺数Re=7.1×107。模型内流道为通流状态,忽略发动机燃烧等情况。
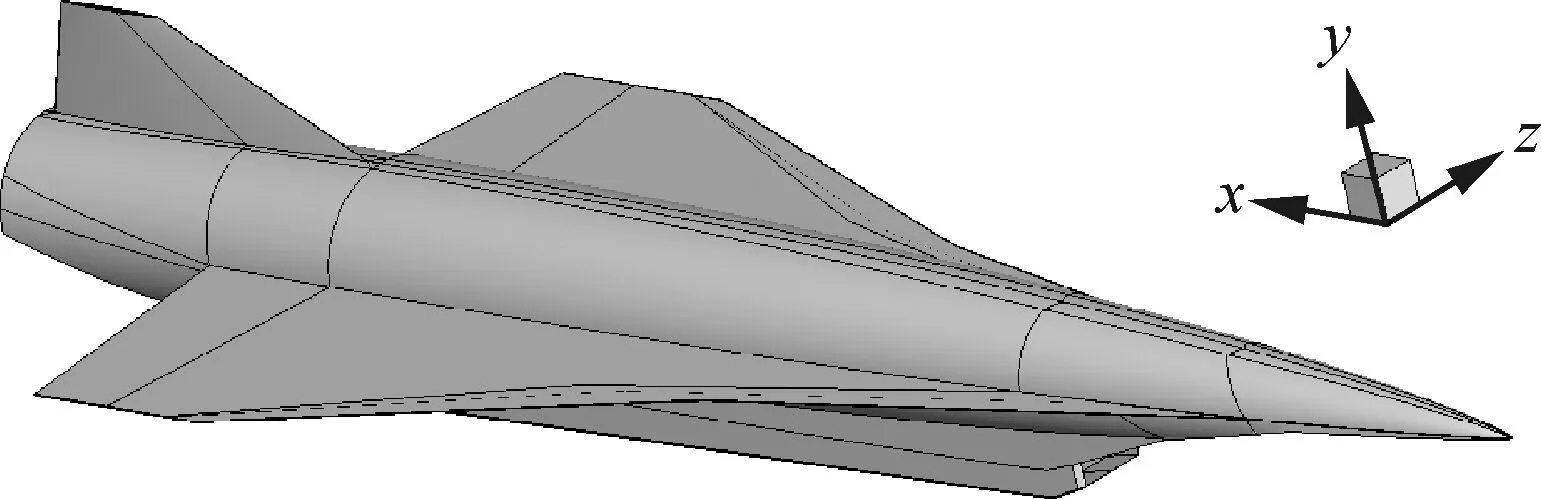
图1 模型几何外形

图2 内流道形状
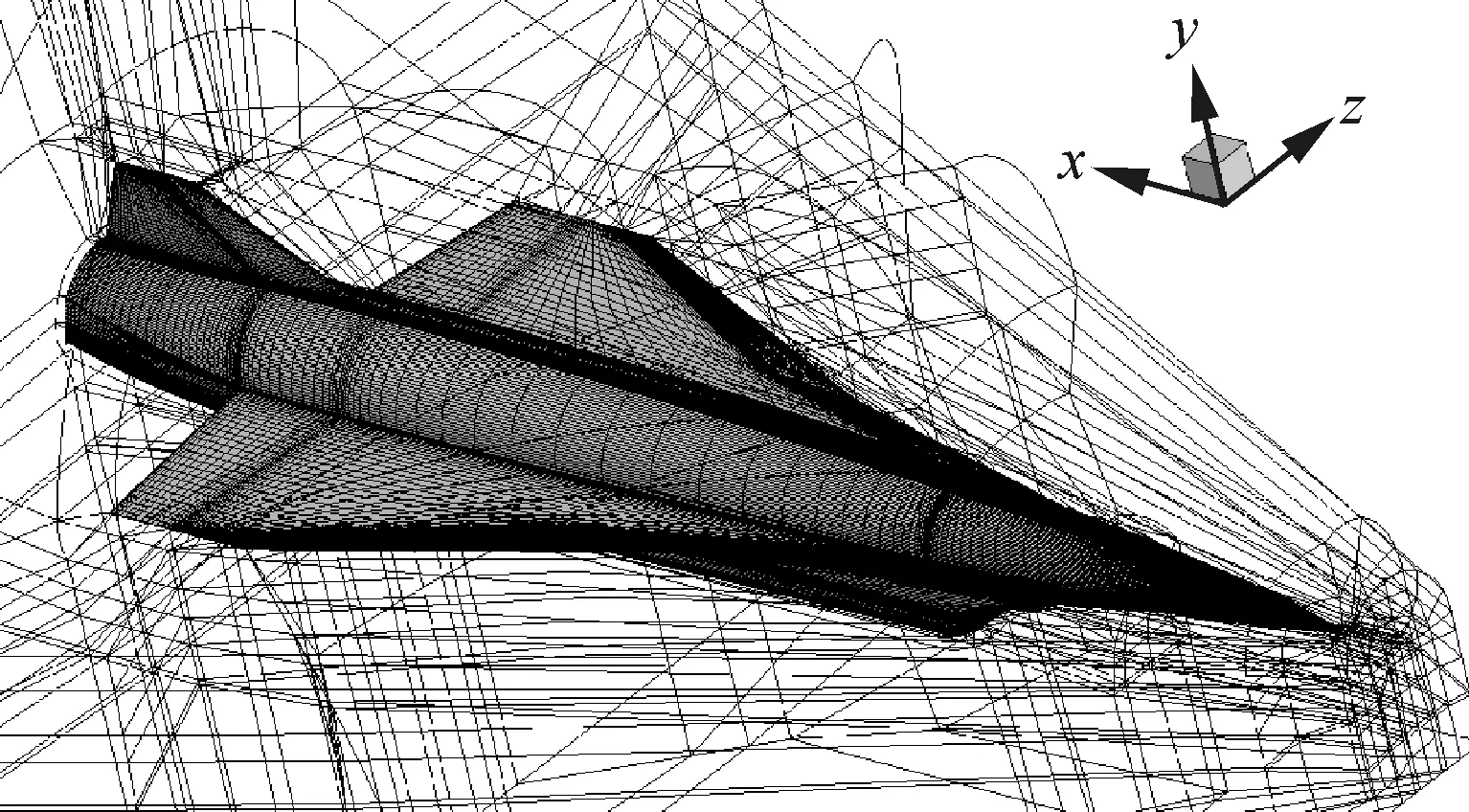
图3 计算网格拓扑
2 验证算例
本节选取Basic Finner导弹标模,利用数值强迫振荡的方法,计算导弹的俯仰、滚转动导数,并与试验结果对比,验证程序对于气动/运动耦合状态下非定常气动力的计算能力。
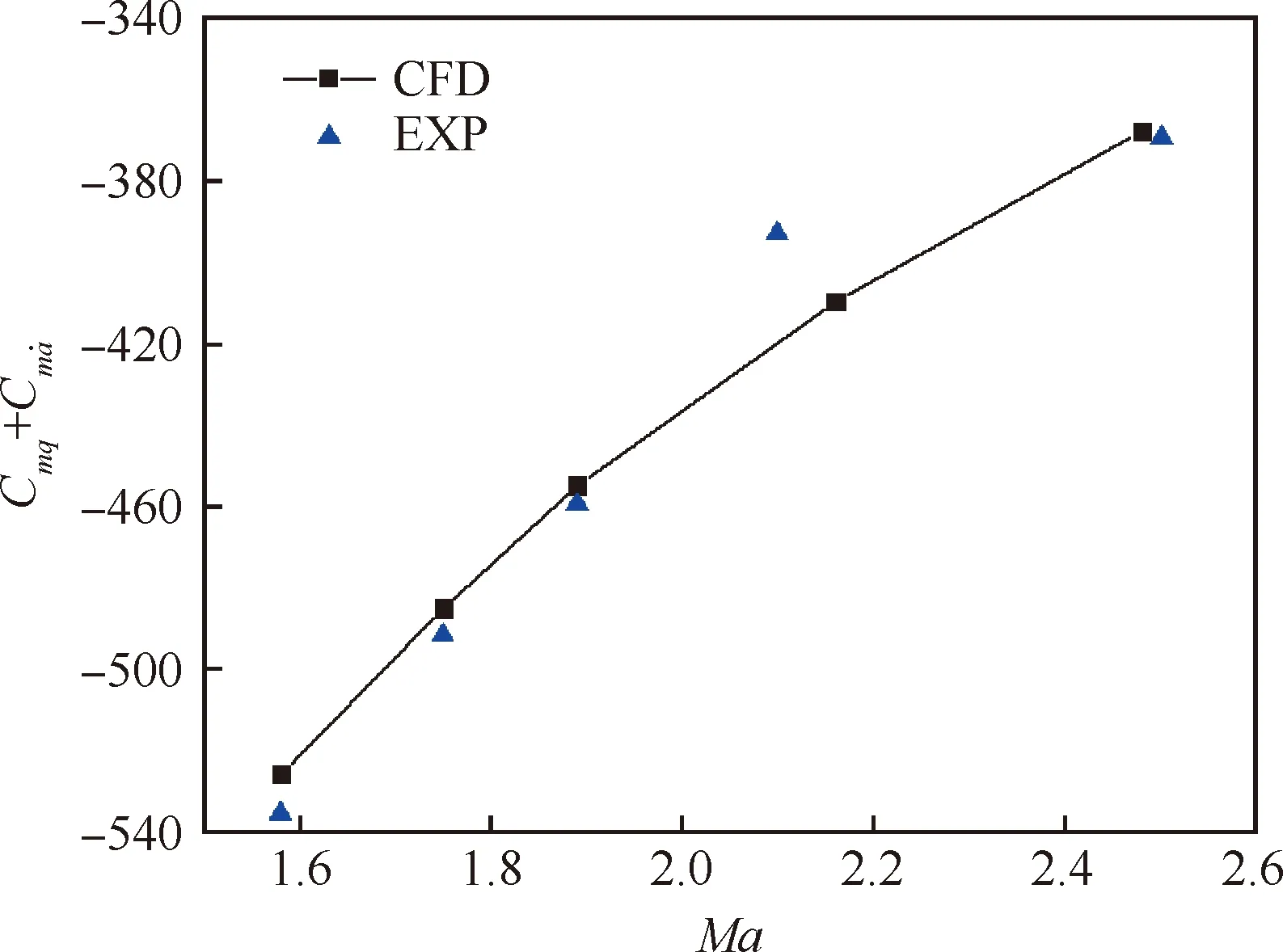
图4 Basic Finner俯仰动导数
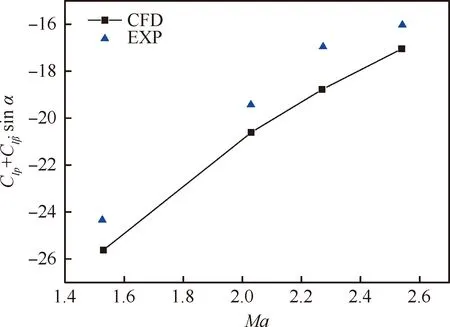
图5 Basic Finner滚转动导数
3 滚转稳定性
3.1 静稳定性
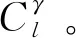
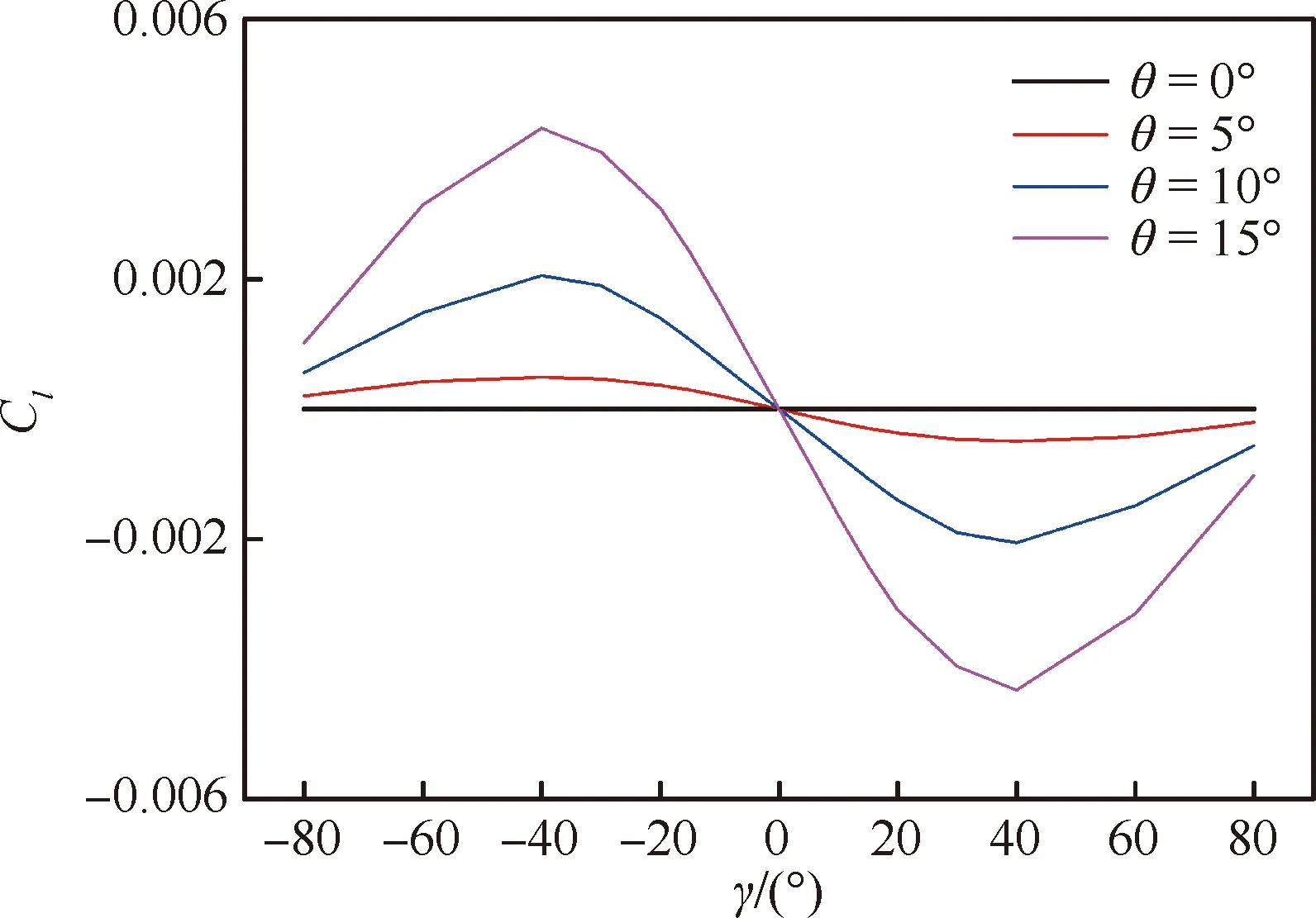
图6 不同俯仰角下滚转力矩系数随滚转角变化
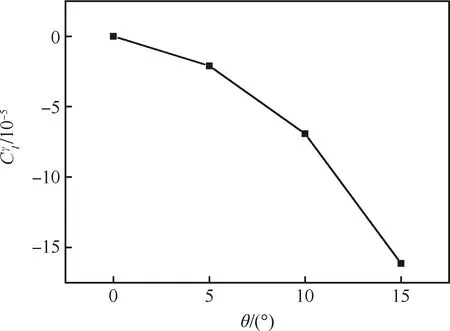
图7 滚转静导数
3.2 动稳定性
由上文可知模型在0°~15°俯仰角下,在一定滚转角范围内具备滚转静稳定性,即模型在平衡状态下受到滚转方向的瞬时扰动时具有恢复到平衡状态的趋势。而模型在受到扰动后的恢复过程以及在平衡位置的敛散特性则是由动稳定性描述的。下面使用数值强迫滚转的方式求得不同俯仰角下模型的滚转动导数,从而评估模型的动稳定性。
强迫滚转振荡运动的滚转力矩系数迟滞曲线如图8所示,迟滞曲线的倾斜程度与图6中静态滚转力矩系数曲线相对应。迟滞曲线的方向如图中箭头所示,为逆时针方向,说明气动力起阻尼作用,模型具备滚转动稳定性。滚转动导数为图9所示,在0°~15°俯仰角下,滚转动导数均小于零,同样说明模型具备滚转动稳定性。其中在俯仰角为5°时滚转动导数的绝对值最小,说明此时滚转运动受到的阻尼最小,滚转动稳定性最差。
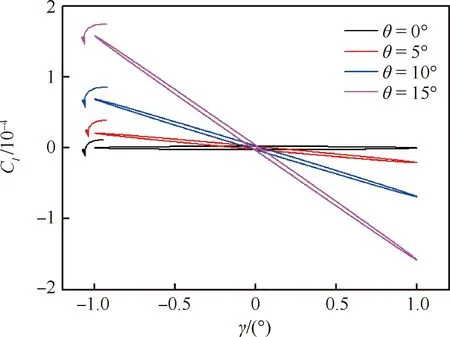
图8 滚转力矩系数迟滞曲线
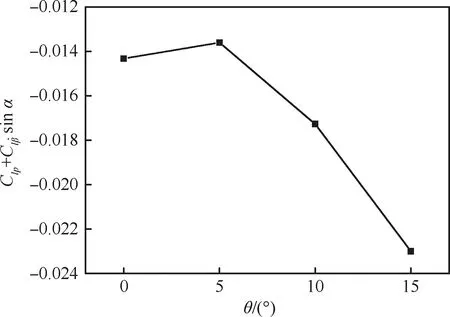
图9 滚转动导数
为了与强迫滚转运动的计算结果进行对比验证,数值模拟了模型在不同俯仰角下的自由滚转运动,模型分别在5°、10°、15°俯仰角下,从5°初始滚转角释放,在气动滚转力矩的作用下自由滚转,逐渐收敛至平衡位置。模型的滚转方向转动惯量Ix为0.1×106kg·m2。数值模拟得到的自由滚转运动曲线如图10所示,运动相图如图11所示。ωx为滚转角速度。随着俯仰角增大,滚转收敛速度变快,滚转频率增大。滚转运动频谱图如图12所示。由图可知θ=5°时,滚转振荡频率f约为0.134 Hz;θ=10°时,滚转振荡频率f约为0.213 Hz;θ=15°时,滚转振荡频率f约为0.372 Hz。
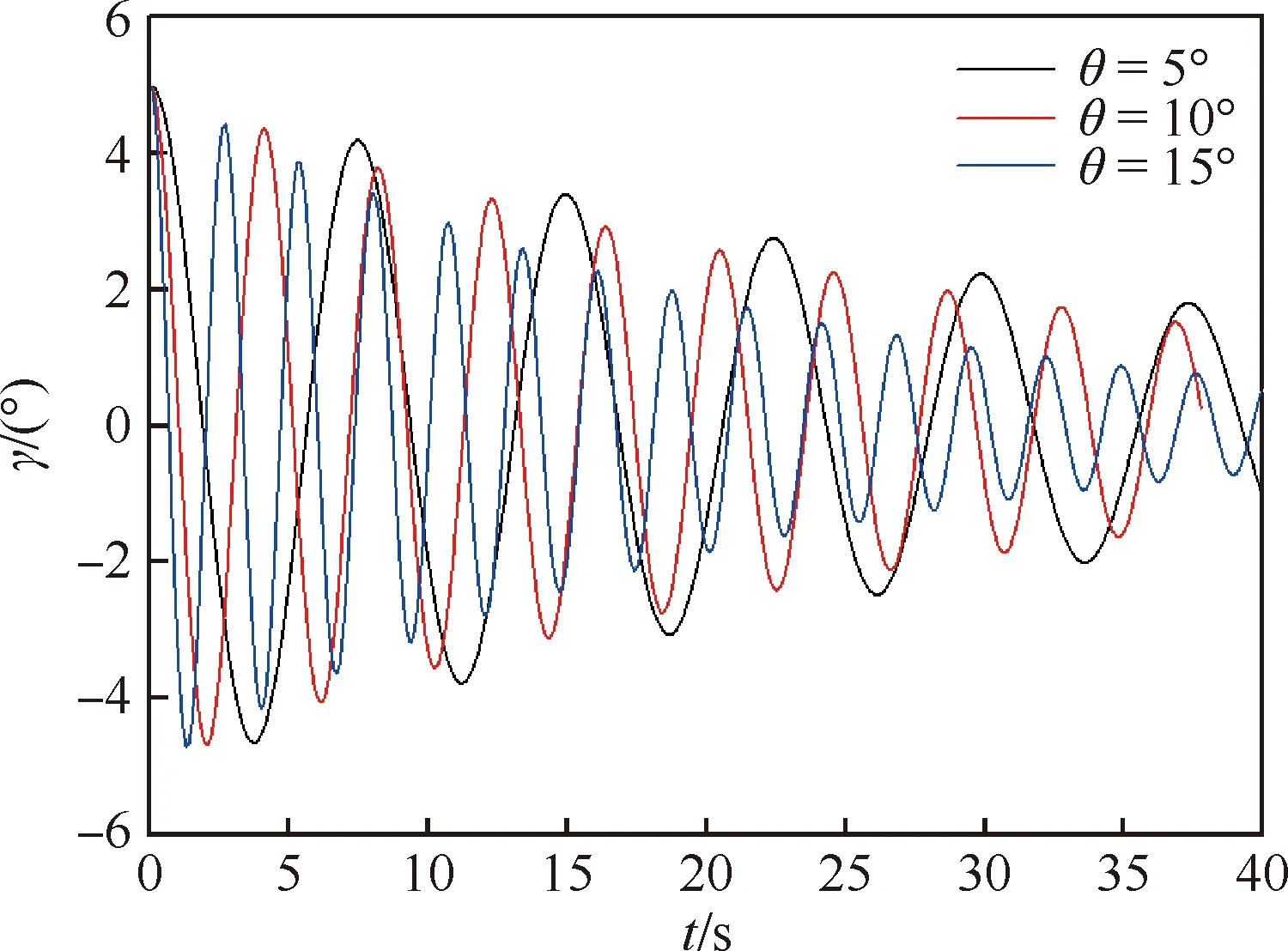
图10 自由滚转运动时滚转角时间历程曲线
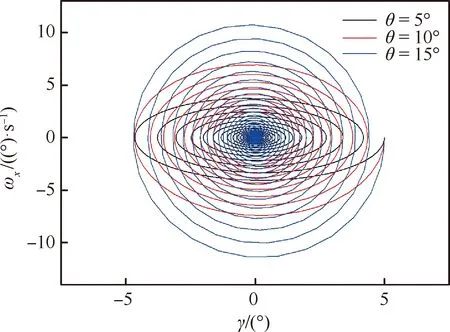
图11 自由滚转运动相图
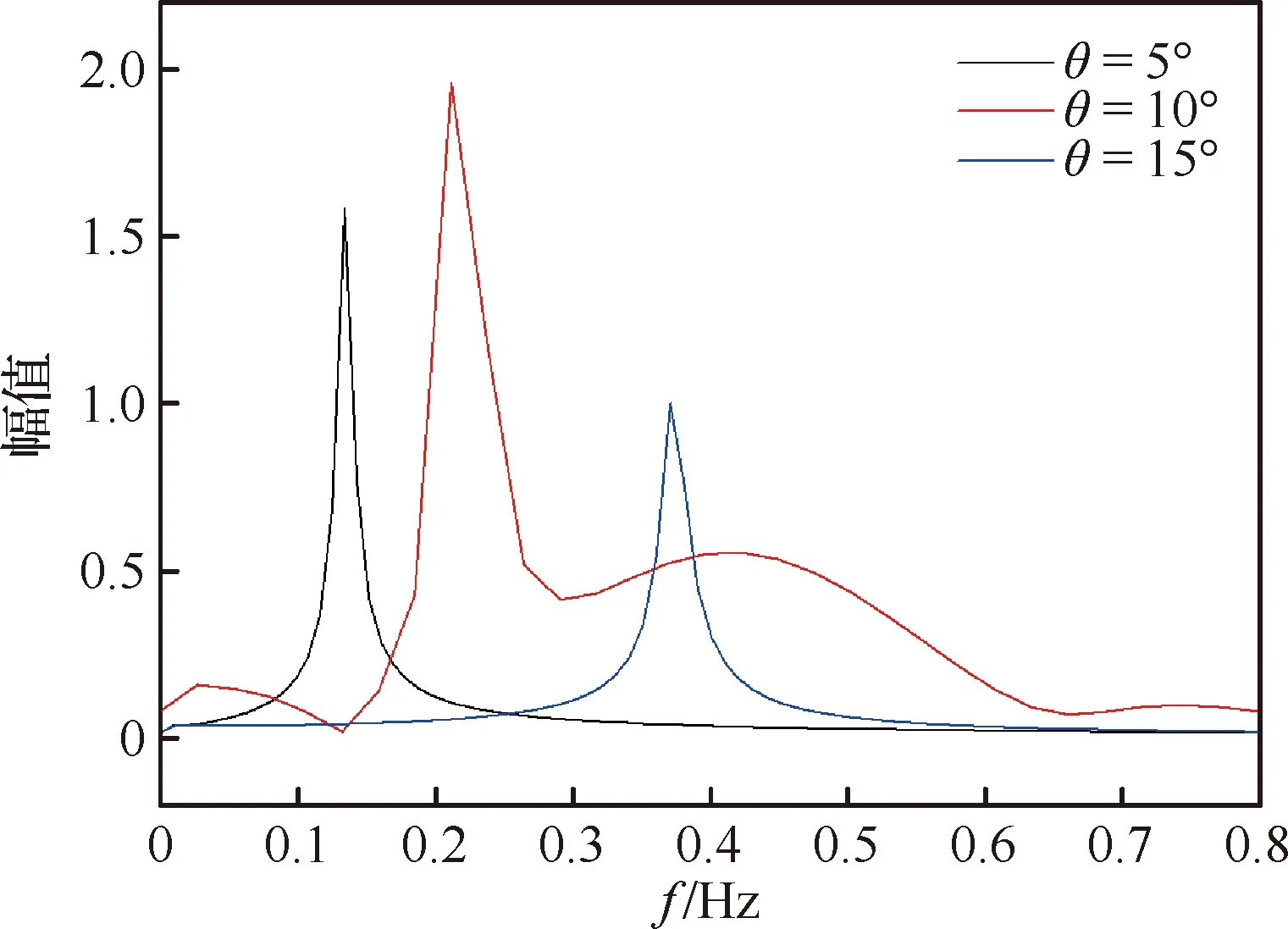
图12 滚转运动频谱图
4 强迫俯仰/自由滚转两自由度耦合运动
在第3节单自由度滚转稳定性研究的基础上,通过数值模拟强迫俯仰/自由滚转运动,进一步研究吸气式高超声速飞行器的气动/运动耦合作用机理,考察在飞行器俯仰运动的过程中滚转通道的稳定性。
4.1 转动惯量影响
为了研究飞行器的转动惯量对强迫俯仰/自由滚转运动带来的影响,参照相似尺寸飞行器的转动惯量分布,针对本文的模型设计了如表1所示的转动惯量工况。对表中工况进行了存在初始滚转角时的强迫俯仰/自由滚转运动数值模拟。模型初始滚转角为5°,强迫俯仰运动为正弦振荡,平均迎角为5°,振幅为5°,频率为0.025 Hz。
首先保持Ix不变,研究Iy、Iz变化带来的影响。由于高超声速飞行器通常采用细长体构型,其滚转方向转动惯量Ix通常远小于偏航和俯仰方向转动惯量Iy、Iz。在飞行器初始滚转角不为0°时,俯仰方向的运动引起的惯性力矩在滚转方向上的分量,也就是惯性耦合力矩可能会对滚转方向产生扰动。由飞行器运动学方程和动力学方程得到惯性耦合力矩M′x的表达式为

表1 模型转动惯量
(1)
针对Case1、Case3,分析不同工况下飞行器滚转角随时间的变化,如图13所示。图中黑色虚线为俯仰角,彩色曲线为不同工况下的滚转角变化曲线。图中3种工况的曲线全部重叠在一起。这是由于俯仰角速度较小,惯性耦合力矩很小,惯性耦合作用对滚转运动的影响可以忽略不计。以Case1工况为例,惯性耦合力矩M′x(黑色曲线)和气动滚转力矩Mx(红色曲线)随时间的变化曲线如图14所示,可以看到Mx比M′x大了3个数量级。这说明滚转方向的运动是由气动力主导的。
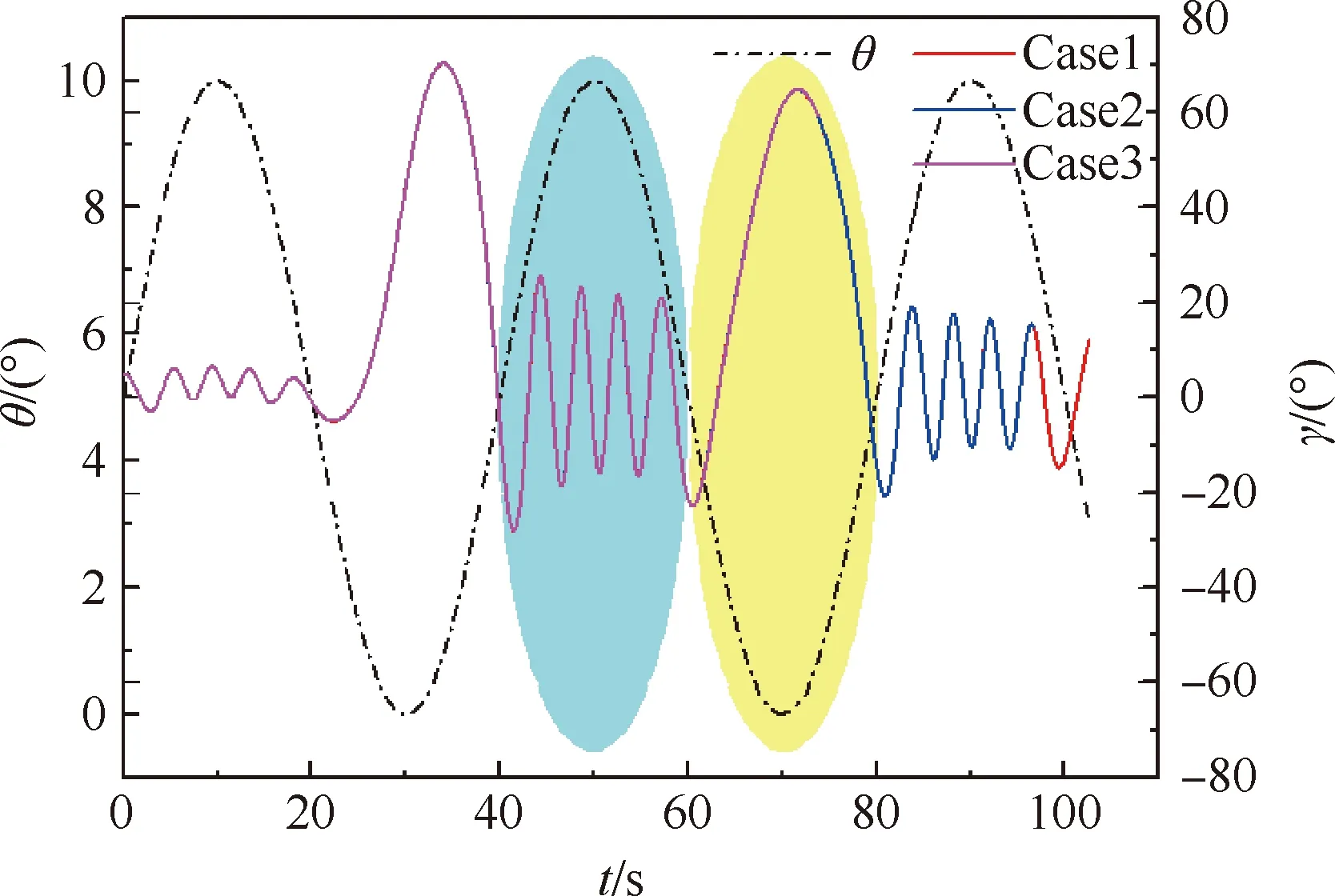
图13 滚转角和俯仰角时间历程曲线(Cases1,2,3)
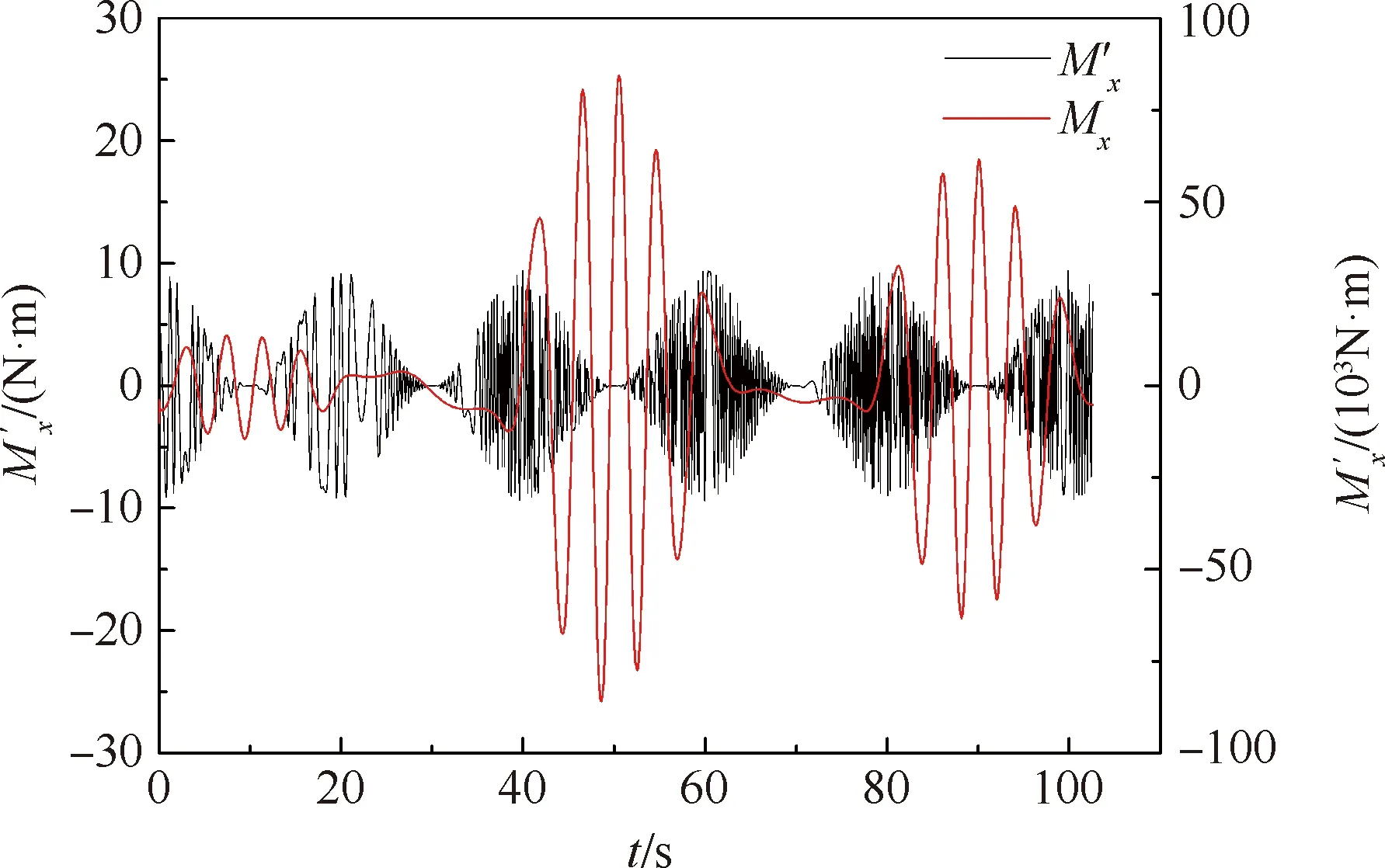
图14 惯性耦合力矩与气动滚转力矩时间历程曲线
在图13中可以看到,随着俯仰角运动区间的不同,滚转角的振动模态呈现拟周期性的变化。如果把俯仰角大于平均振幅的周期称为上半周期,如t=40~60 s(图中蓝背景区域),小于平均振幅的称为下半周期,如t=60~80 s(图中黄背景区域),可以发现,除去前20 s,在俯仰角上半周期存在滚转角约为15°的中等振幅振荡,频率较高,而在下半周期,滚转角以超过60°振幅进行大振幅振荡,且振动频率与俯仰角振荡基本频率一致。
尽管上文对滚转稳定性的研究表明模型在滚转方向具有静稳定性和动稳定性,但在强迫俯仰/自由滚转耦合运动的过程中,模型在滚转方向出现了中等振幅的振荡,并在θ=0°的位置附近出现了滚转角约70°的振荡。这说明单自由度运动的动导数不能对两自由度耦合运动进行准确预测。
叶友达、田浩等[10-11]在研究类HTV-2高超声速飞行器两自由度耦合运动时提出了两自由度稳定性判据:
(2)
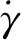
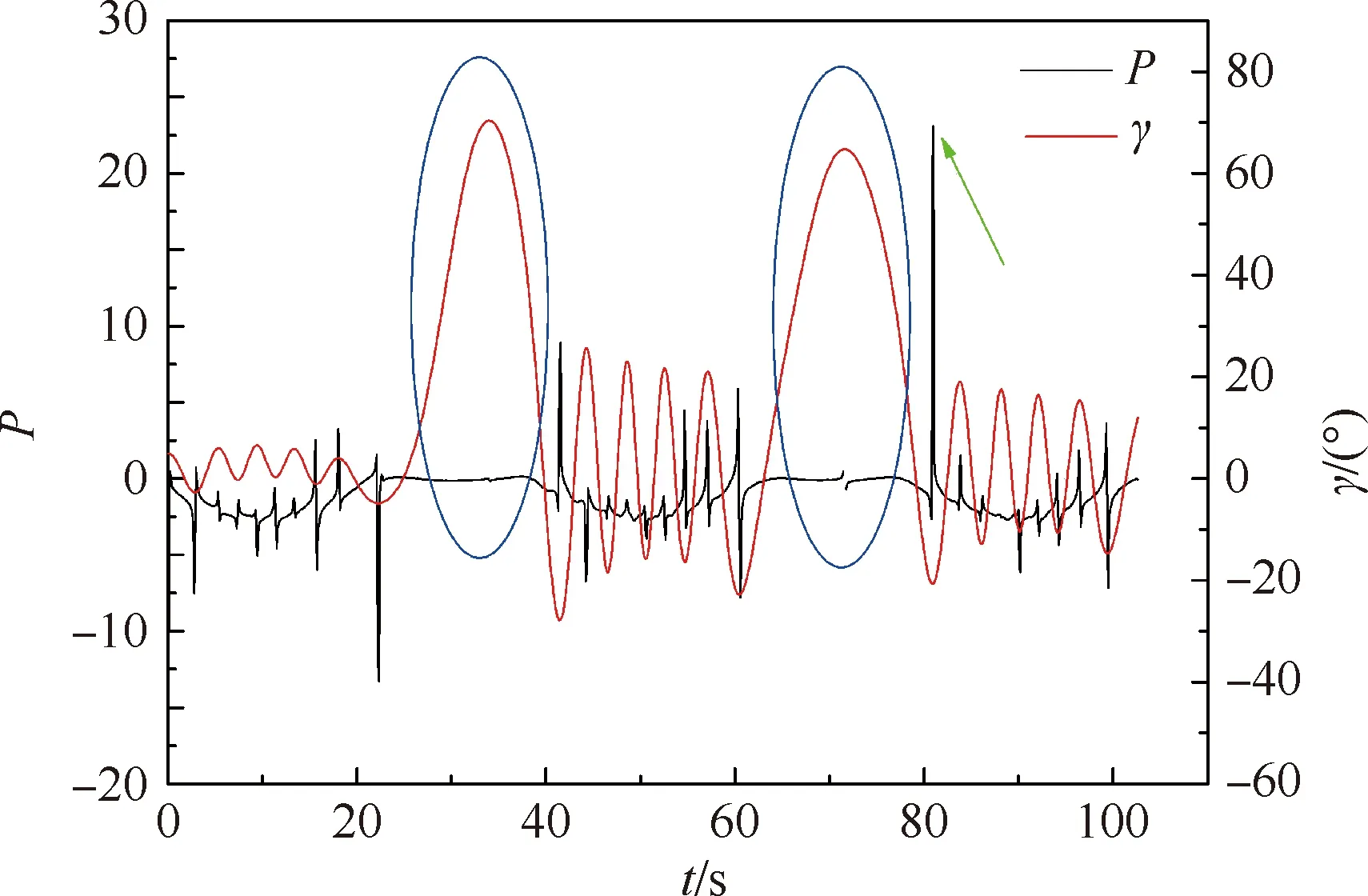
图15 判据P和滚转角时间历程曲线
接下来保持Iy、Iz不变,研究Ix变化带来的影响。针对Case2、4、5,分析不同工况下飞行器滚转角随时间的变化如图16所示。可以看出Ix变化对滚转角的运动规律影响较为明显。在俯仰角上半周期,滚转角振动频率随Ix的增大而减小,滚转角的振幅随着Ix的增大而 明显增大,Case5(Ix=0.05×106kg·m2)最大振幅只有13°,Case4(Ix=0.2×106kg·m2)最大振幅达到40°。而在俯仰角下半周期,滚转角的振幅也随着Ix的增大而增大,但变化相对较小。
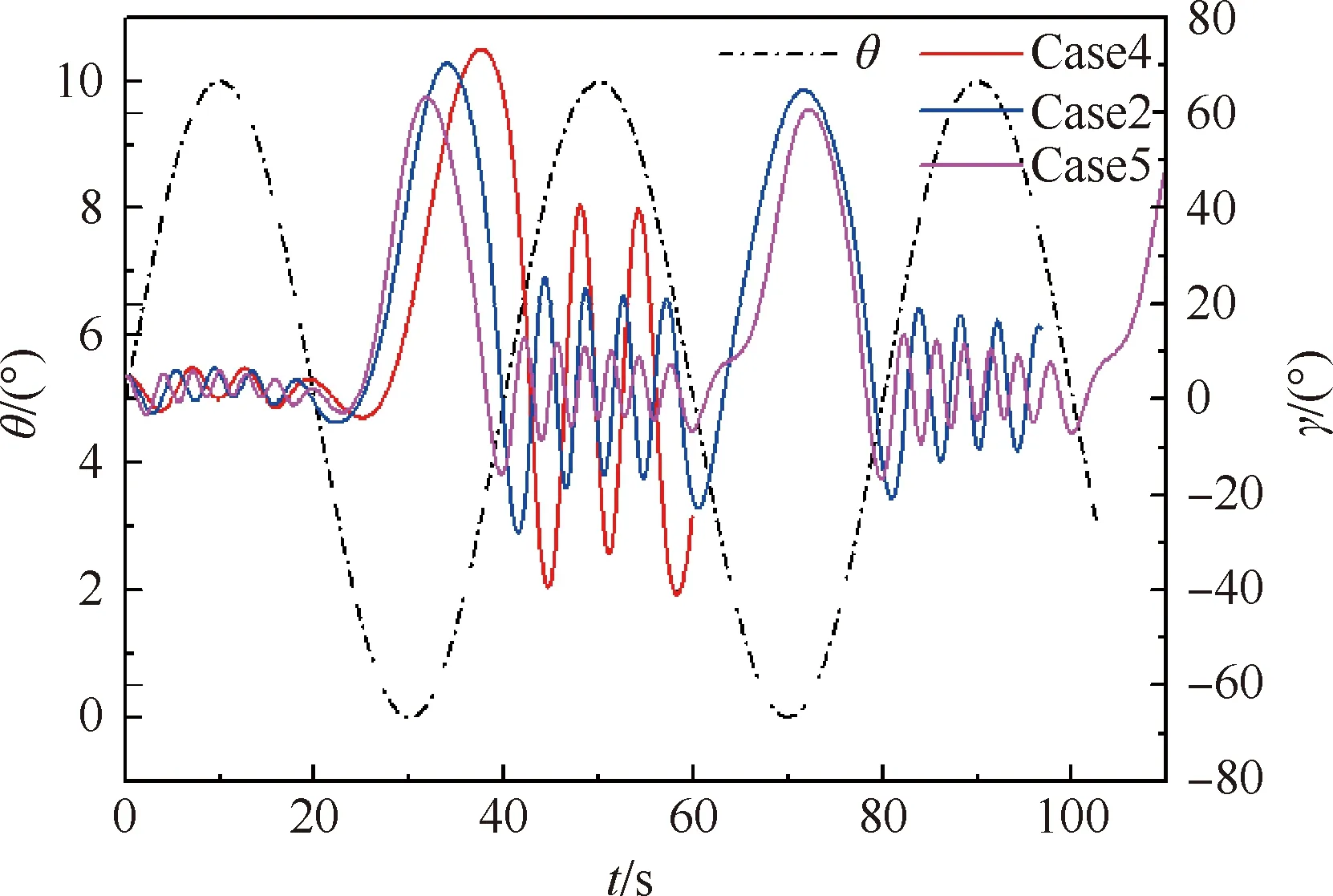
图16 滚转角和俯仰角时间历程曲线(Cases2,4,5)
4.2 俯仰运动频率影响
下面针对俯仰运动频率的影响展开进一步的研究。保持模型初始滚转角5°,强迫俯仰运动为正弦振荡,平均迎角5°,振幅5°,模型惯量分布与Case2保持一致,分别对f=0.012 5 Hz和f=0.037 5 Hz的工况进行数值模拟,并与f=0.025 Hz的工况结果进行对比。
f=0.012 5 Hz和f=0.037 5 Hz工况下滚转角随时间的变化如图17和图18所示。f=0.012 5 Hz工况下,在俯仰角的上半周期滚转振荡的振幅小于10°,在下半周期超过50°。f=0.037 5 Hz 工况下,在俯仰角的上半周期滚转振荡的振幅约为20°,在下半周期超过60°。结合前文Case2工况俯仰角振荡频率为f=0.025 Hz的滚转角变化曲线可以看出,在俯仰运动的上半周期,滚转角振荡频率随俯仰角振荡频率的变化较小,而在下半周期的大幅振荡频率则与俯仰角振荡频率基本一致。
f=0.012 5,0.025,0.037 5 Hz 3种工况的滚转相图如图19所示,纵轴为滚转角速度。可以看到在3种工况下,相图均为类似极限环的形态,一个半径较小的圆形极限环与一个扁平的椭圆形极限环交替出现,两个极限环分别对应上半周期的中小幅度振荡以及下半周期的大振幅振荡。在图中可以看出圆环半径随俯仰运动频率的增加而增大,表明上半周期振幅受俯仰运动频率影响较大;而椭圆形右端位置变化较小,表明下半周期振幅受俯仰运动频率影响较小。
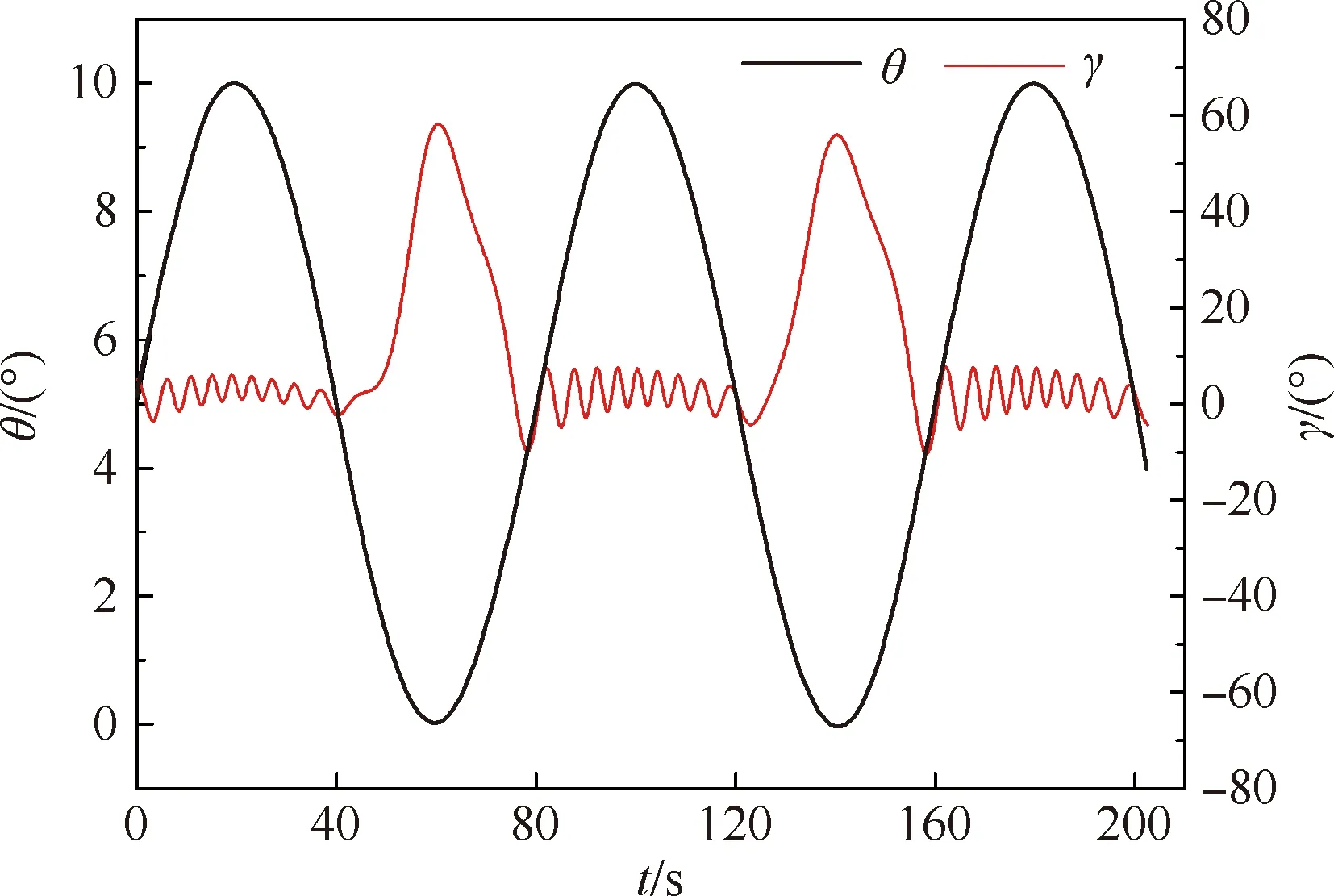
图17 f=0.012 5 Hz工况滚转角和俯仰角时间历程曲线
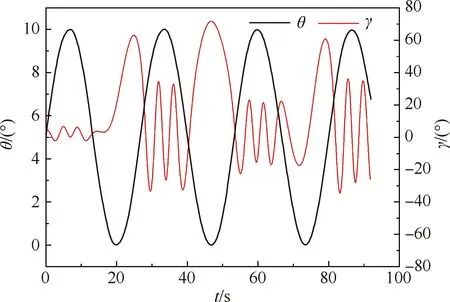
图18 f=0.037 5 Hz工况滚转角和俯仰角时间历程曲线
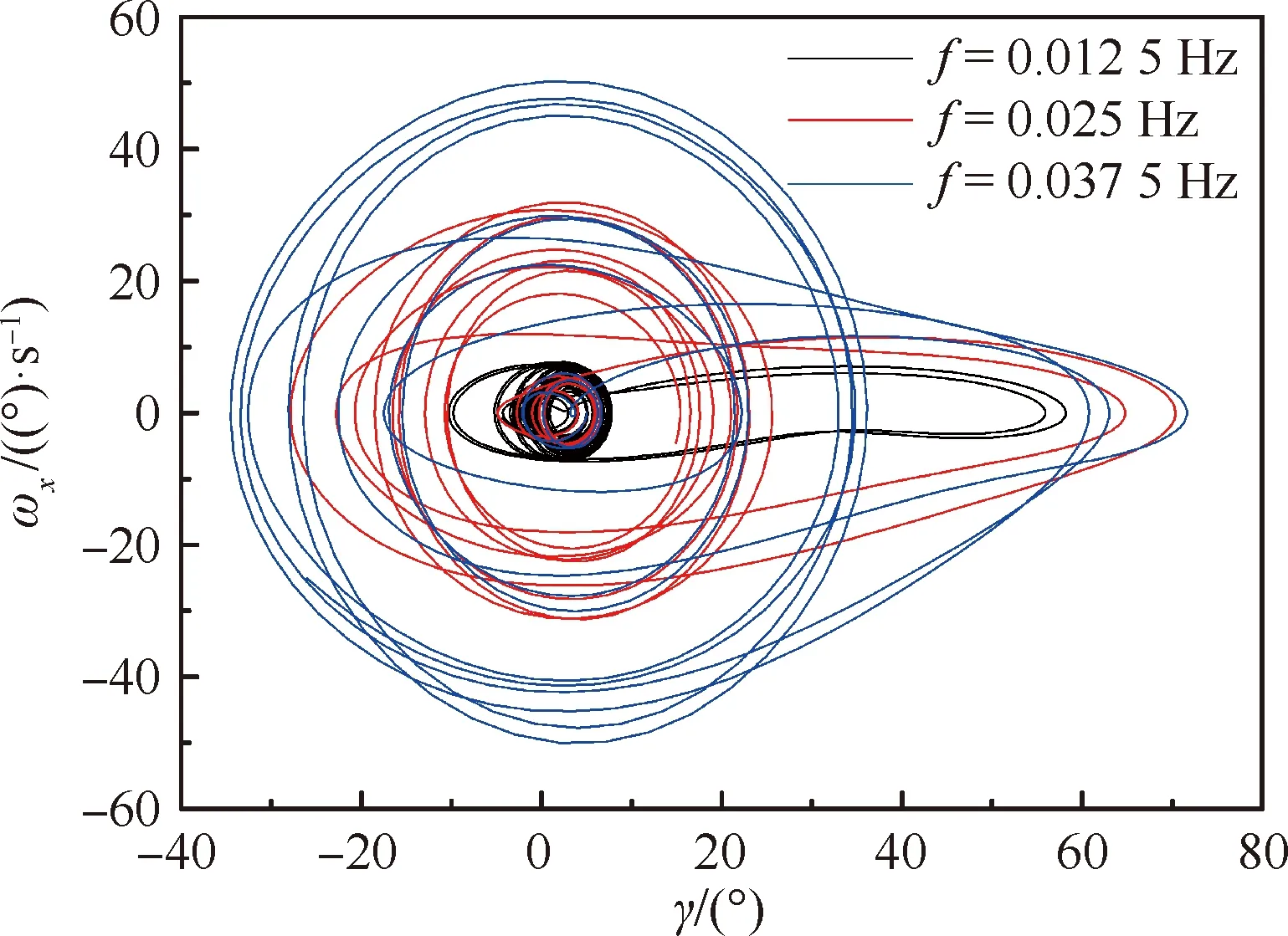
图19 滚转角速度-滚转角相图
4.3 耦合运动机理分析
上文研究了飞行器转动惯量以及俯仰频率对飞行器耦合运动的影响,可以发现在各个工况下滚转方向的运动都呈现为高频中小幅振荡与低频大幅振荡交替出现的趋势。下面对耦合运动进行稳定性分析[24-25]。
飞行器的气动滚转力矩Mx在平衡态附近可以展开为
(3)
由于飞行器的惯性耦合作用可以忽略,滚转方向的运动学方程和动力学方程可表示为
(4)
式(4)可进一步写为
(5)
选取Case1作为典型工况进行具体分析,该工况下滚转力矩系数以及俯仰角、侧滑角、滚转角随时间的变化曲线如图20所示。可以看到,在滚转角高频振荡的区间,例如40~60 s范围内,飞行器的俯仰角超过5°,此时飞行器的侧滑角随着飞行器的滚转角而剧烈振荡,使得飞行器在滚转的过程中获得了较大的滚转回复力矩,维持飞行器的高频滚转振荡。而在60~80 s范围内,飞行器的俯仰角逐渐减小至0°后回到5°,在此期间,虽然飞行器出现了大幅滚转,但侧滑角始终小于2°,滚转力矩系数非常小且变化缓慢,静稳定性差,无法在短时间内改变飞行器的滚转方向。飞行器在俯仰角接近0°的位置出现滚转角大幅震荡,这种现象与Adamczak和Bolender[21]对同样采用翼身组合体构型的HIFiRE-6一体化飞行器的动态特性研究时指出的飞行器受到的气动阻尼较小,在小迎角下横侧向通道动不稳定的结论有一定相似性。说明本文的研究结论对采用类似构型的飞行器有一定的参考价值。
飞行器在60~80 s这个滚转角大幅振荡的区间内滚转力矩系数随滚转角的变化曲线如图21所示。曲线为双“8”字型,曲线左右两端呈逆时针旋转,表明飞行器的滚转运动受到气流的阻尼作用,向气流释放能量,而曲线的中间部分呈顺时针旋转,表明气流向飞行器的滚转运动输入能量。这种能量输入输出与俯仰方向的运动有关。图20中红色虚线位置为俯仰角为0°的时刻,可以看到由于滚转角达到峰值的时刻滞后于俯仰角达到0°的时刻,在滚转角增大的过程中对应的俯仰角小于滚转角减小的过程中对应的俯仰角,这种差异导致了滚转过程中能量的输入和耗散。
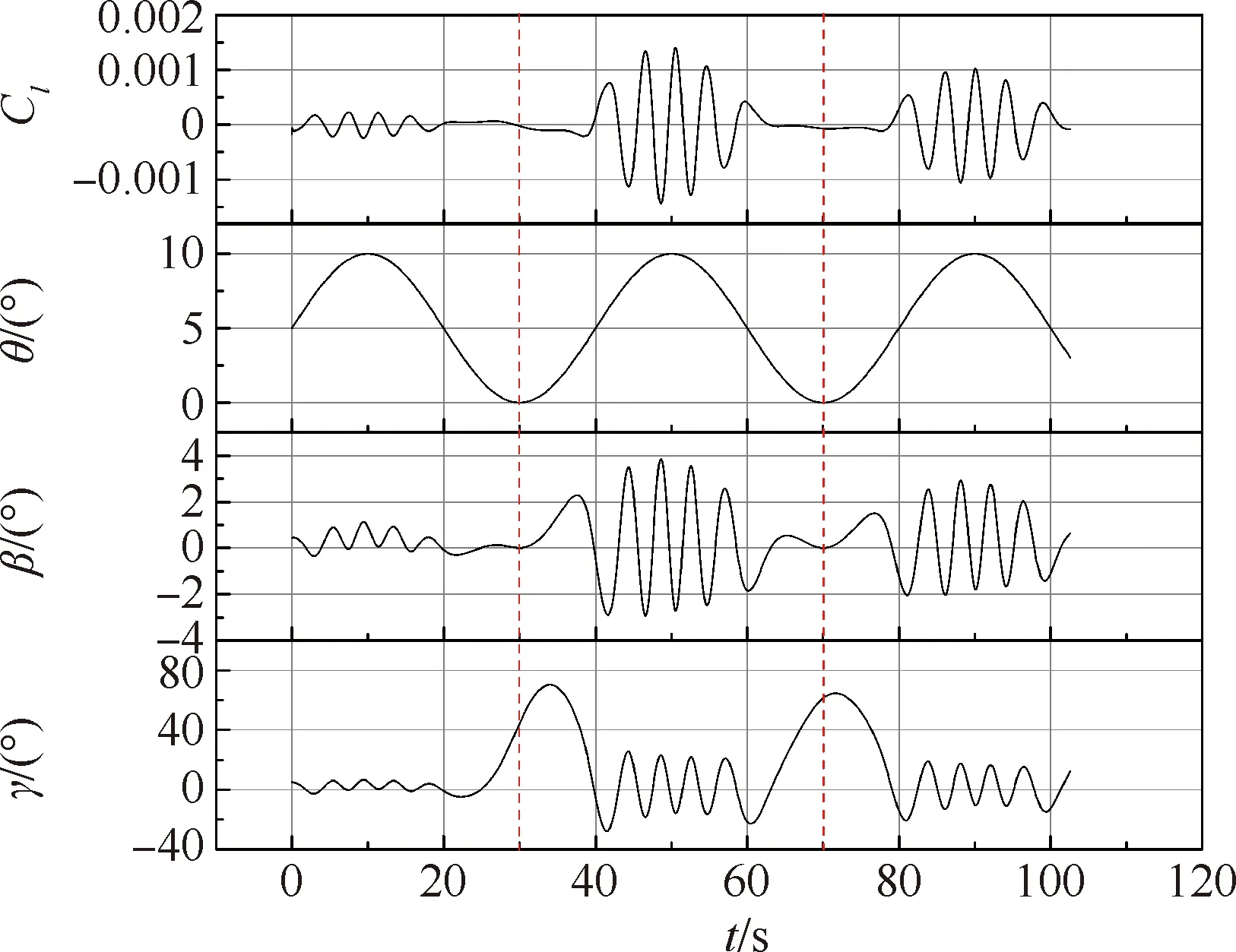
图20 滚转力矩系数、俯仰角、侧滑角和滚转角时间历程曲线
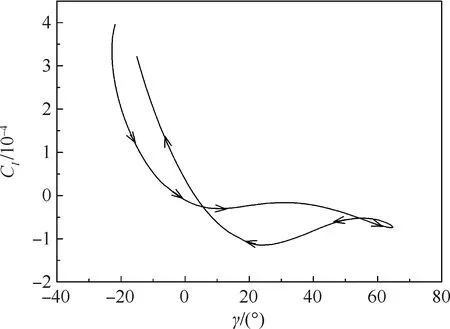
图21 滚转力矩系数随滚转角的变化
5 结 论
1) 虽然模型具有滚转静稳定性和动稳定性,但是在强迫俯仰/自由滚转运动过程中,滚转通道却出现了中小幅度振荡与大振幅振荡交替出现的情况。中小幅度振荡出现在俯仰运动的上半周期,大振幅振荡出现在俯仰运动的下半周期,俯仰角接近0°的位置,最大滚转角超过70°,这说明单自由度运动的动导数不能对两自由度耦合运动进行准确预测。
2) 由于俯仰角速度较小,惯性耦合力矩很小,因而Iy、Iz变化对耦合运动带来的影响可以忽略。而Ix对俯仰运动上半周期出现的滚转角中小幅振荡影响较为明显,滚转角振动频率随Ix的增大而减小,振幅随着Ix的增大而明显增大。
3) 俯仰运动频率对上半周期出现的滚转振荡振幅影响较为明显,对滚转振荡频率影响较小。振幅随俯仰运动频率的增大而增大。
4) 滚转角增大的过程中对应的俯仰角小于滚转角减小的过程中对应的俯仰角,这种差异导致了大振幅滚转振荡过程中能量的输入和耗散。
