材料参数随温度变化的功能梯度圆筒热弹性分析

吴雨桐

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引 言

功能梯度材料(functionally graded materials,FGM)是指构成材料的组成、结构沿厚度方向由一侧向另一侧呈连续梯度变化,从而使材料性质和功能也呈梯度变化的一种新型材料[1],因其良好的力学与热学性能适用于高温环境。功能梯度空心圆筒和圆柱结构是工程中的常用结构,而温度荷载也是其在工作过程中常见的荷载类型。因此,研究功能梯度圆筒热弹性问题对该类材料结构的设计和应用具有重要的理论指导意义。

在功能梯度圆筒的热弹性分析中,由于材料性质随梯度改变,且热传导方程中还包含了温度对时间的偏导数,使得求解过程非常复杂。Shao等[2]采用Laplace变换,借助Galerkin法和级数法,得到了功能梯度圆筒热弹性场的半解析解。Darabseh和Bani-Salameh[3]采用一种基于隐式差分格式的数值方法,计算得到了功能梯度圆柱的热弹性场分布。通过使用一种摄动解法,果立成等[4]研究了功能梯度圆柱壳在热冲击载荷下的瞬态温度场和瞬态热应力场。盛宏玉等[5-6]将状态空间理论与有限差分法相结合,对层合材料和组合实心圆柱进行了瞬态热传导分析。

目前在求解功能梯度圆筒瞬态热弹性问题时以积分变换法居多,求解过程烦琐,且材料参数随温度变化属于复杂的非线性问题,很多相关研究都没有将其考虑在内。马永斌等[7]和何天虎等[8]虽考虑了温度对材料参数的影响,但为了简化计算,在材料参数与温度相关的函数中用材料初始温度代替了变化的温度场,这在温度变化较大的条件下计算结果有较大的误差。本文在空间上使用状态空间技术,时域内应用有限差分格式,可将某时刻求得的温度场应用到下一时刻材料参数与温度相关的函数中,从而得到该热弹性问题的准非线性解,精度能得到进一步提升,且方法简便,计算效率高。陈新宇[9]应用本文方法对材料参数只沿径向坐标变化的功能梯度圆筒热弹性问题进行了分析,并与文献[2]进行了对比,验证了本文方法的正确性和有效性。

1 基本方程

考虑一内、外半径分别为a和b的无限长弹性圆筒,其横截面与所建坐标系如图1所示。材料的物理参数κ、λ、α和弹性参数E和ν分别表示其热扩散率、热传导系数、热膨胀系数、弹性模量和泊松比。除泊松比外，其他几项均为关于径向坐标r以及温度场T的函数。假设圆筒初始时刻的温度T0均匀分布,内、外环境温度分别为Ta和Tb,且保持不变,则该情况属于轴对称平面应变问题。圆筒在环境温度作用下,产生一维瞬态温度场、位移场和应力场。

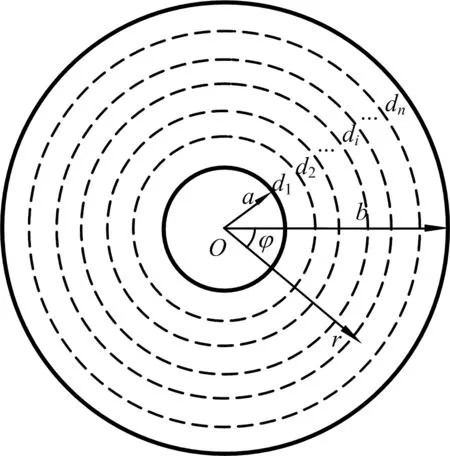
图1 功能梯度圆筒的横截面及坐标和分层示意图

傅里叶方程和能量守恒方程在该问题下的表达式分别为:

(1)

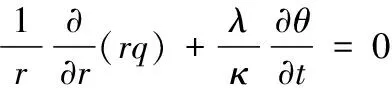
(2)

式中:q为热流密度;θ=T-T0,为圆筒的温度场相对于初始温度的温差。

在不计体力时,圆筒平衡方程为:

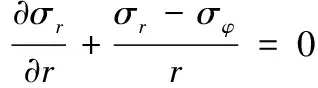
(3)

热弹性应力和位移关系为

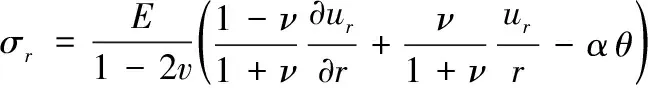
(4)

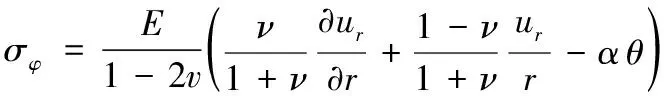
(5)

式中:σr和σφ分别表示圆筒径向和环向应力。

初始条件设为:

θ(r,0)=0

(6)

边界条件设为:

σr(a,t)=0,σr(b,t)=0

q(a,t)=βa[θa-θ(a,t)],q(b,t)=βb[θ(b,t)-θb]

(7)

式中:θa=Ta-T0,θb=Tb-T0;βa和βb分别代表圆筒在与外界进行对流换热时的传热系数。

2 状态方程的建立与求解

由式(4)可得:

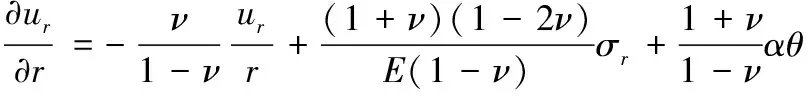
(8)

将式(4)和式(5)代入到平衡方程式(3)中,再利用式(8)得:

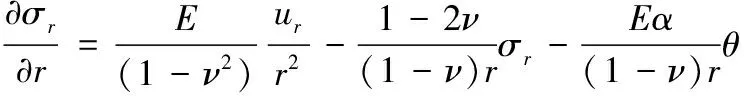
(9)

于是,式(1)、式(2)、式(8)和式(9)构成了一个偏微分方程组,其矩阵形式为:

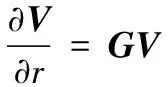
(10)

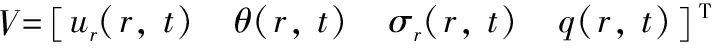
由于方程的系数矩阵中材料参数不仅沿圆筒径向坐标变化,还与圆筒的温度变化有关,式(10)为变系数非线性偏微分方程组,求解过程十分复杂,因此需要进行如下几个方面的处理。

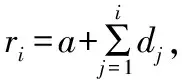
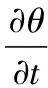
(11)

式中:[θ(r,t)]k表示t=tk时刻的温度场。

将式(11)代入式(10)中,在系数矩阵中取径向坐标r=hi=(ri+ri-1)/2,并在材料参数与温度相关的函数中代入tk-1时刻的温度场,最终得到tk时刻关于第i层子壳的一阶非齐次常微分方程组,即状态方程:

(ri-1≤r≤ri,i=1,2,3,…,n)

(12)

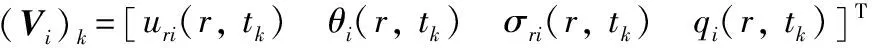
对式(12)积分可得到状态向量

[Vi(r,t)]k=Di(r-ri-1)[Vi(ri-1,t)]k+[Hi(r,t)]k,

(ri-1≤r≤ri)

(13)

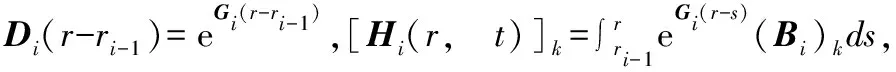
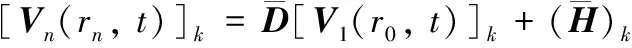
(14)

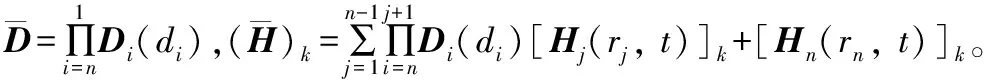
利用初始条件(6)和边界条件(7),由式(12)～(14)可以求出任意时刻在任意位置处的状态变量。

3 算例和结果分析

下面考虑材料参数在空间上沿径向呈连续函数变化的功能梯度圆筒,为便于分析,做以下无量纲变换:

(R,A,B)=(r,a,b)/rm,E*=E/E0,α*=α/α0,

Θa,Θb)=(θ,θa,θb)/T0,

(∑r,∑θ)=(σr,σθ)/(α0T0E0),Ur=ur/α0T0rm,

Ha=rmβa/λa,Hb=rmβb/λb

式中:E0、α0、λ0、κ0为材料参考值;λa、λb分别表示圆筒内、外壁的导热系数;rm为参考半径,rm=(a+b)/2。

这里考虑一内、外半径分别为a=0.9 m和b=1.1 m的功能梯度圆筒。参考半径rm=1 m,材料各参数的参考值为E0=225 GPa,α0=4.8×10-6K-1,λ0=5.9 W(mk)-1,κ0=2.8×10-6m2/s,ν=0.3。假定圆筒的初始温度为参考温度T0,内、外表面突然置于温度为Θa=1和Θb=0的环境中,且环境温度Θa和Θb保持不变,圆筒的内、外表面传热系数分别为Ha=30和Hb=55。设圆筒的材料参数分布服从以下函数:

E*=em1(R-A)·f(T*),α*=em2(R-A)·f(T*)

λ*=em3(R-A)·f(T*),κ*=em4(R-A)·f(T*)

(15)

式中：取m1=2.0,m2=0.3,m3=3.0,m4=2.0；f(T*)为无量纲温度函数。

Rishin等[10]在研究了金属的弹性模量与温度之间的关系后指出,材料的弹性模量随温度的增加而减小。为便于分析,在一般情况下,设温度函数

f(T*)=1-ηT*

(16)

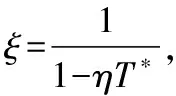
为得到足够收敛的解,在计算中将圆筒沿厚度方向分为100层,时间步长取Δτ=0.0001。

图1给出当时间τ=0.002、0.005和达到稳态后不同初始温度相关参数ξ0下温度Θ沿径向R的分布。从图1可以看出,在靠近圆筒内壁附近区域,随着ξ0的增加,同一时刻和位置的圆筒温度会升高,而在其他区域,随着ξ0的增加,同一时刻和位置的圆筒温度会降低。但总的来说,在该算例中,温度相关参数对圆筒温度场的影响很小。

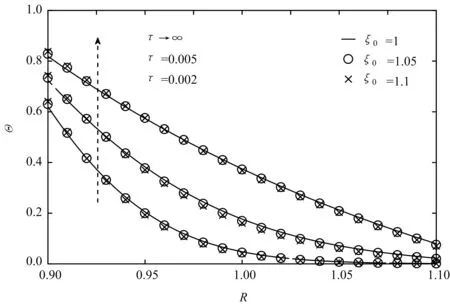
图1 功能梯度圆筒温度沿径向分布

图2给出当时间τ=0.002、0.005和达到稳态后不同初始温度相关参数ξ0下径向位移Ur沿径向R的分布。从图2可以看出,温度相关参数对圆筒径向位移有较大的影响。初始温度相关参数ξ0越大,同一时刻圆筒径向位移越小,随着时间的增加,圆筒内部温度升高,温度相关参数ξ也会增加,材料参数的数值会随ξ的增加而减小,进而使得圆筒径向位移相对减小幅度更大。从图中还可以看出,同一时刻在不同的ξ0下,圆筒内部各点的径向位移变化幅度相近。

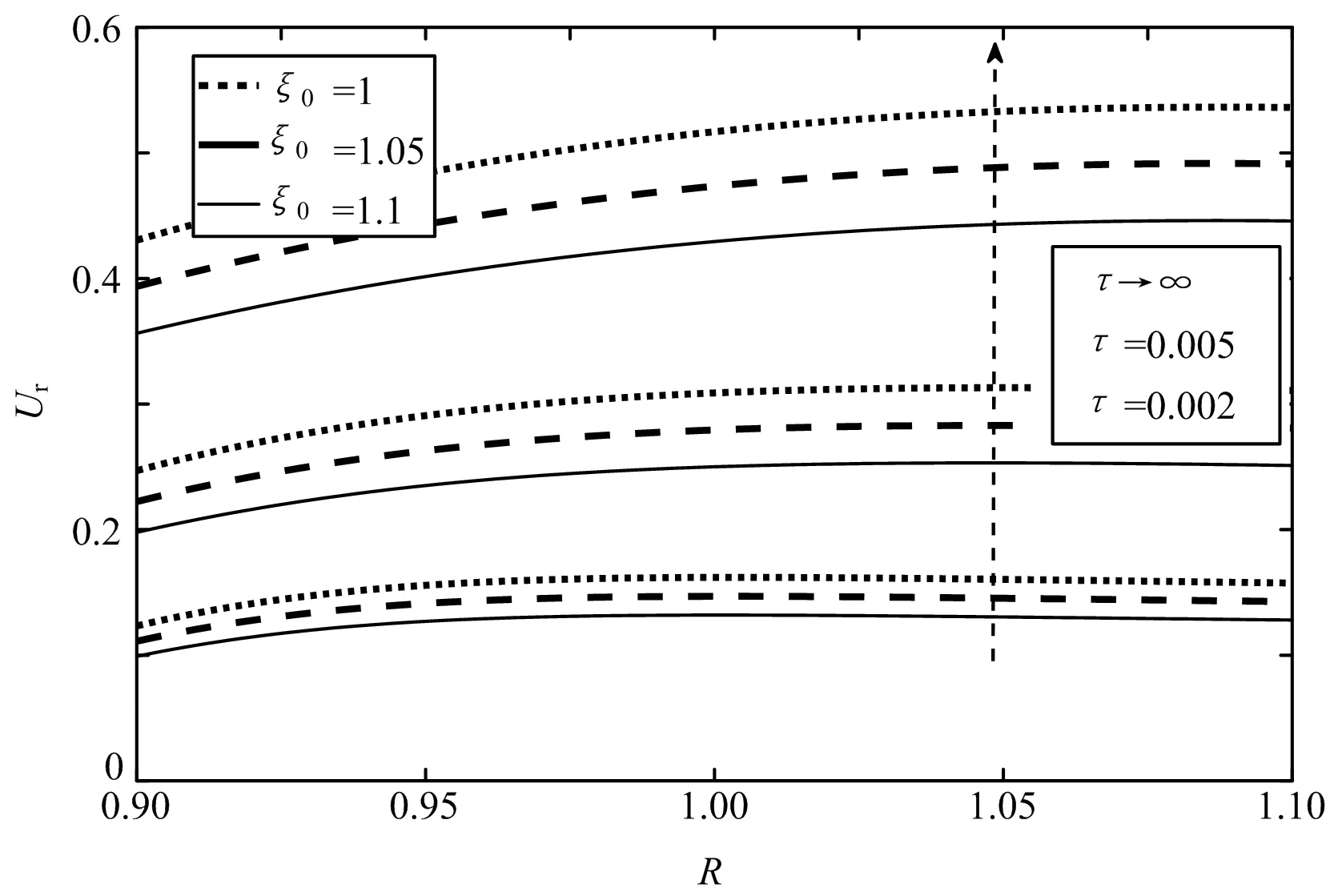
图2 功能梯度圆筒径向位移沿径向分布

图3给出当时间τ=0.002、0.005和达到稳态后不同初始温度相关参数ξ0下径向应力Σr沿径向R的分布。从图3可以看出,温度相关参数对圆筒径向应力的影响很大。初始温度相关参数ξ0越大,在同一时刻圆筒径向应力的绝对值越小,且不同ξ0之间的径向应力差异十分明显。由于和径向位移相同的原因,随着时间的增加,径向应力绝对值相对减小的幅度越大。图中还可以看出,同一时刻在不同ξ0下,靠近圆筒中部附近位置的径向应力变化幅度更大。

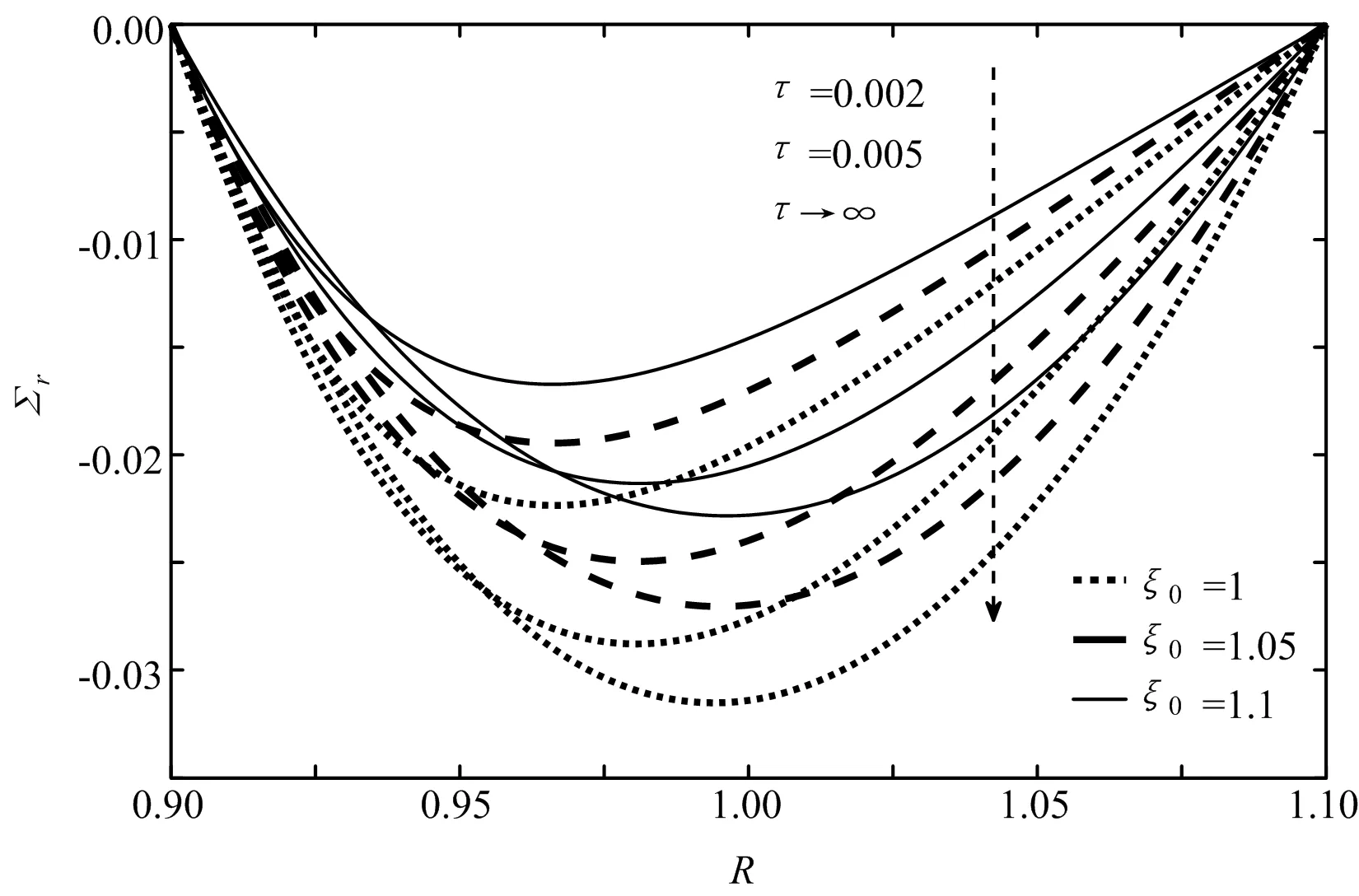
图3 功能梯度圆筒径向应力沿径向分布

为了分析本文对温度函数的处理方法与文献[7]中处理方法之间的误差,以对圆筒径向应力分布的分析为例,图4给出了当ξ0=1.05时,不同处理方法下圆筒径向应力分布之间的差别对比。由于文献[7]中对温度函数式(16)进行线性化处理时,用不变的初始温度T0*代替了变化的温度场T*,也就是说,温度相关参数始终保持为ξ0不变。而从图1可以看出,圆筒内部的温度升高幅度较大,则ξ会发生较大的改变,因此不能忽略温度变化所带来的影响。从图4可以看出,文献[7]的处理方法与本文的处理方法计算出的结果误差较大,由于本文在计算过程中考虑了ξ会随着温度的增加而增加,因此得到的径向应力绝对值要更小(其他物理量同理)。随着时间的增加,圆筒内部温度升高,两种方法得到的径向应力之间差异也就更加明显。

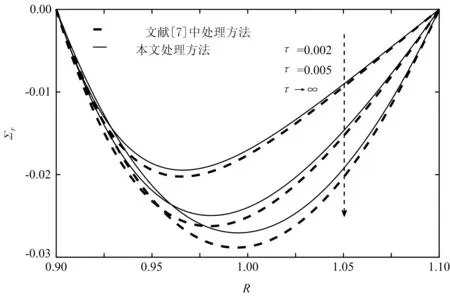
图4 ξ0=1.05时对温度函数不同的处理方法得到的径向应力分布差异对比

4 结 论

本文基于傅里叶定律、能量守恒方程、热弹性方程和平衡方程,在空间上使用状态空间技术,时域内应用有限差分格式,建立了圆筒热弹性问题在轴对称平面应变条件下的状态空间理论,得到了材料参数随温度以及沿径向任意梯度变化的圆筒热弹性问题的状态空间解。算例表明,温度相关参数的增加会使材料参数的数值减小,从而使圆筒各物理量有不同程度的降低。相较于文献[7]的线性化方法,本文通过迭代的方式在求解该类非线性问题时可以使计算精度得到提高,过程更简便,计算效率更高。此外,本文方法能够满足轴对称平面应变问题下的多种边界条件,还能退而求解均匀材料的相关问题。