铝模早拆体系独立支撑承载性能研究

杨皓东， 仰树燕

(1.安徽建筑大学 土木工程学院，安徽 合肥 230601； 2.合肥建工集团有限公司，安徽 合肥 230088)

0 引 言

铝模体系中，早拆体系独立支撑至关重要，由楼面和梁底早拆系统组成[1,2]。早拆技术施工原理是：对早拆头、主次梁和可调钢立杆组成的整体，通过增加竖向支撑点，使构件由长跨承重变为短跨承重，降低构件内力，待混凝土达到其设计强度的一半，拆除模板，钢支撑和早拆头保持不动，其余模板和支架通过预留传料口传递至下一流水施工[3-6]。铝模支撑形式与扣件式钢管不同，步距大、无水平拉杆，且目前大多数研究是针对整体模架，对于单支撑的试验和研究成果比较少，因此对单支撑施工承载性能的研究非常有必要。

1 单支撑承载力理论计算

铝模多用于高层住宅，而住宅普遍高度为2.9 m，因此取2.7 m单支撑作为研究对象。单支撑规格为：φ60×2.2套管套住φ48×2.5插管，内管孔洞直径为15 mm，销键直径为14 mm。

根据《建筑施工计算手册》[7]，单支撑的承载力可按四种破坏形态进行计算，其中最小值即为支撑的承载力设计值。计算结果见表1。

表1 四种计算模式下钢支撑的承载力

因此，单支撑的容许承载力计算值为13.52 kN。

2 单支撑承载力试验研究

本次针对2.7 m和3.1 m单支撑进行了试验，具体以2.7 m为例。

2.1 试验目的、内容、测点布置及加载方案

(1)试验目的：进一步验证单支撑的施工承载力和变形。

(2)试验内容：利用反力架、千斤顶、压力传感器和测力计，进行竖向加载，在单支撑上贴应变片，顶点和中点放置位移计，如图1所示，测出单支撑屈服承载力、极限承载力和变形。

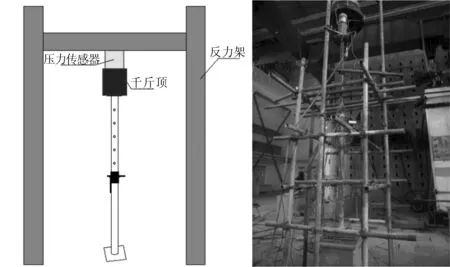
图1 试验装置示意图

(3)测点布置：每隔15 cm贴一圈(钢管四周)应变片，测点分别为A、B、C、D、E、F，G，如图2所示。

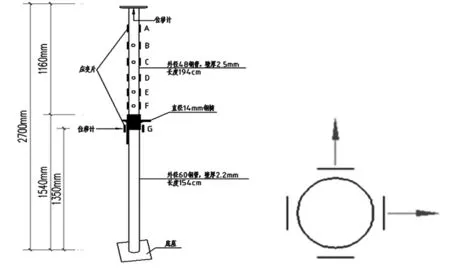
图2 应变片和位移计分布示意图

(4)加载方案：先预加2 kN，持荷10 min后卸载，检测试验装置是否完备；再按每级2 kN正式加载，持荷2 min，当加载至理论计算的容许承载力后，每级加载1 kN，每次持荷2 min，一直加至钢支撑发生失稳破坏；最后当荷载加至测力计读数上不去时，进行卸载。

2.2 试验结果及分析

2.7 m(3.1 m)立杆的顶点和中点位移变化如图3(图4)所示。

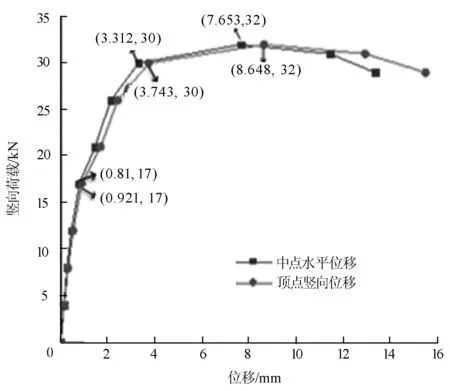
图3 2.7 m立杆顶点、中点位移-荷载曲线

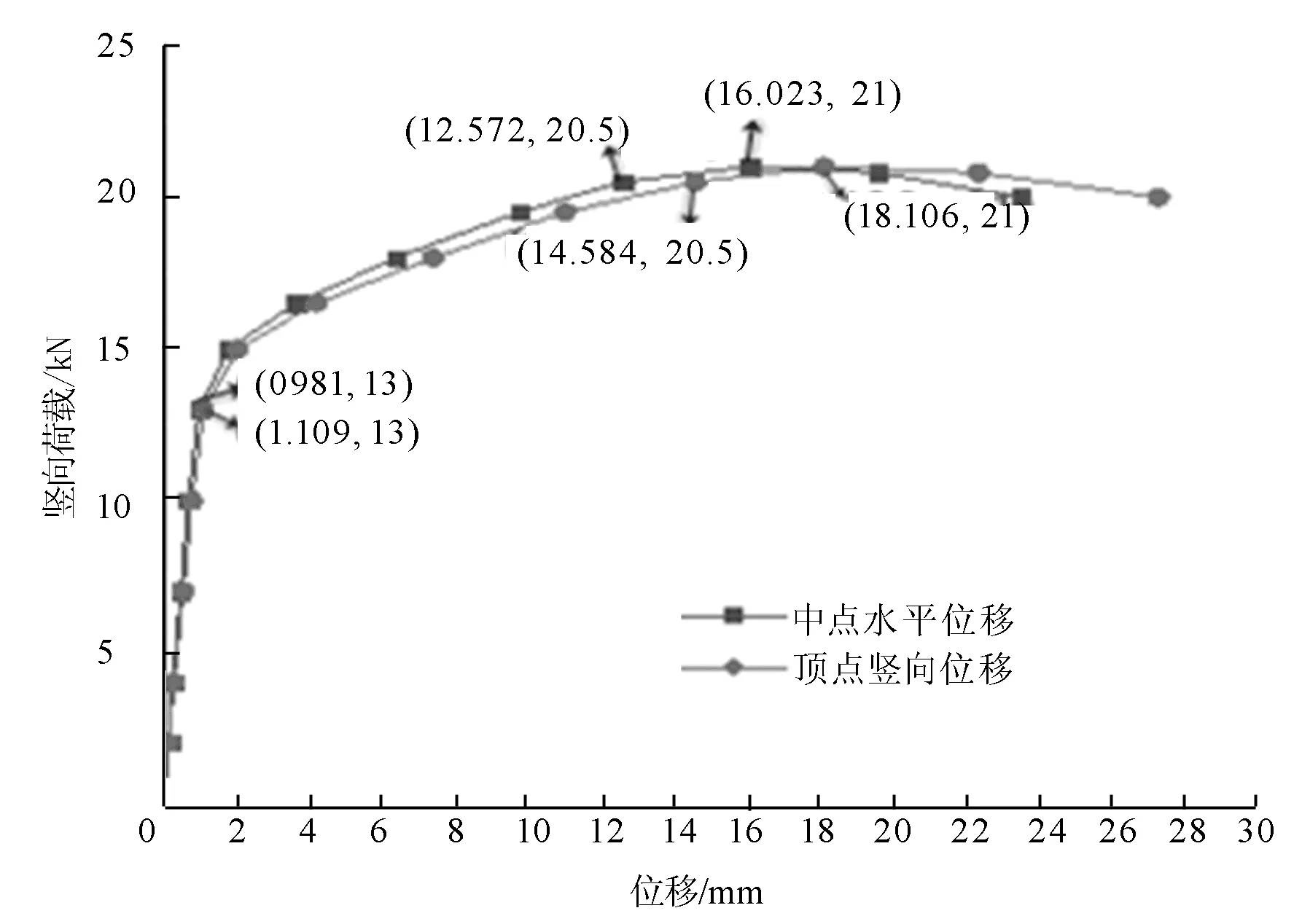
图4 3.1 m立杆顶点、中点位移-荷载曲线

由图3、图4可知：

(1)曲线呈线性变化阶段——非线性上升阶段——较缓台阶段——峰值(最高点)——下降阶段，由此可知立杆在竖向荷载作用下，发生了三个变化阶段，即弹性阶段——弹塑性阶段——破坏阶段。

(2)17 kN(13 kN)是立杆弹性阶段临界点，此阶段立杆水平和竖直位移均只发生微小变化。30 kN(20.5 kN)是弹塑性临界点。32 kN(21 kN)是曲线最高点，随后曲线呈下降趋势，立杆变形加大，力却在减小，说明此荷载即为立杆的极限荷载。而将17 kN(13 kN)作为立杆的弹性临界点，原因是：图3(图4)中位移曲线的0～17 kN(0～13 kN)阶段各点两两之间的角度变化不大，该段曲线呈线性关系，此后各阶段的曲线斜率发生明显的偏差。

(3)顶点竖向位移与中点水平位移相差不大，误差在13%～16%，最大误差仅为16%，平均误差为14%。这是相对合理的，故可通过中点水平位移来研究立杆的变形。

3 单支撑有限元模拟分析

3.1 模型建立

立杆为内外套管式，φ60×2.2套管套住φ48×2.5插管，使用高度2.7 m，内管开孔直径为15 mm，底座为120 mm×120 mm×3 mm，钢管采用Q235B级钢，材料参数见表2。

表2 单支撑材料参数

根据以上工况，先创建部件，再定义立杆的材料和截面属性。内外管采用壳单元，连接部位通过耦合完成，立杆的顶部和底部是铰接形式。创建完立杆的材料和截面属性后，设置分析步，在钢管顶部施加竖向集中荷载，一直加至钢支撑达到极限状态。

3.2 模拟结果

对立杆进行后屈曲分析，失稳变形如图5所示。

图5 立杆屈曲变形

(1)弹性荷载和极限荷载。模拟分析得到，立杆的弹性荷载临界点为17.8 kN，弹塑性临界点为31.6 kN，加至34 kN时，达到极限状态，进入破坏阶段。

(2)位移值。中点荷载-位移曲线如图6所示。

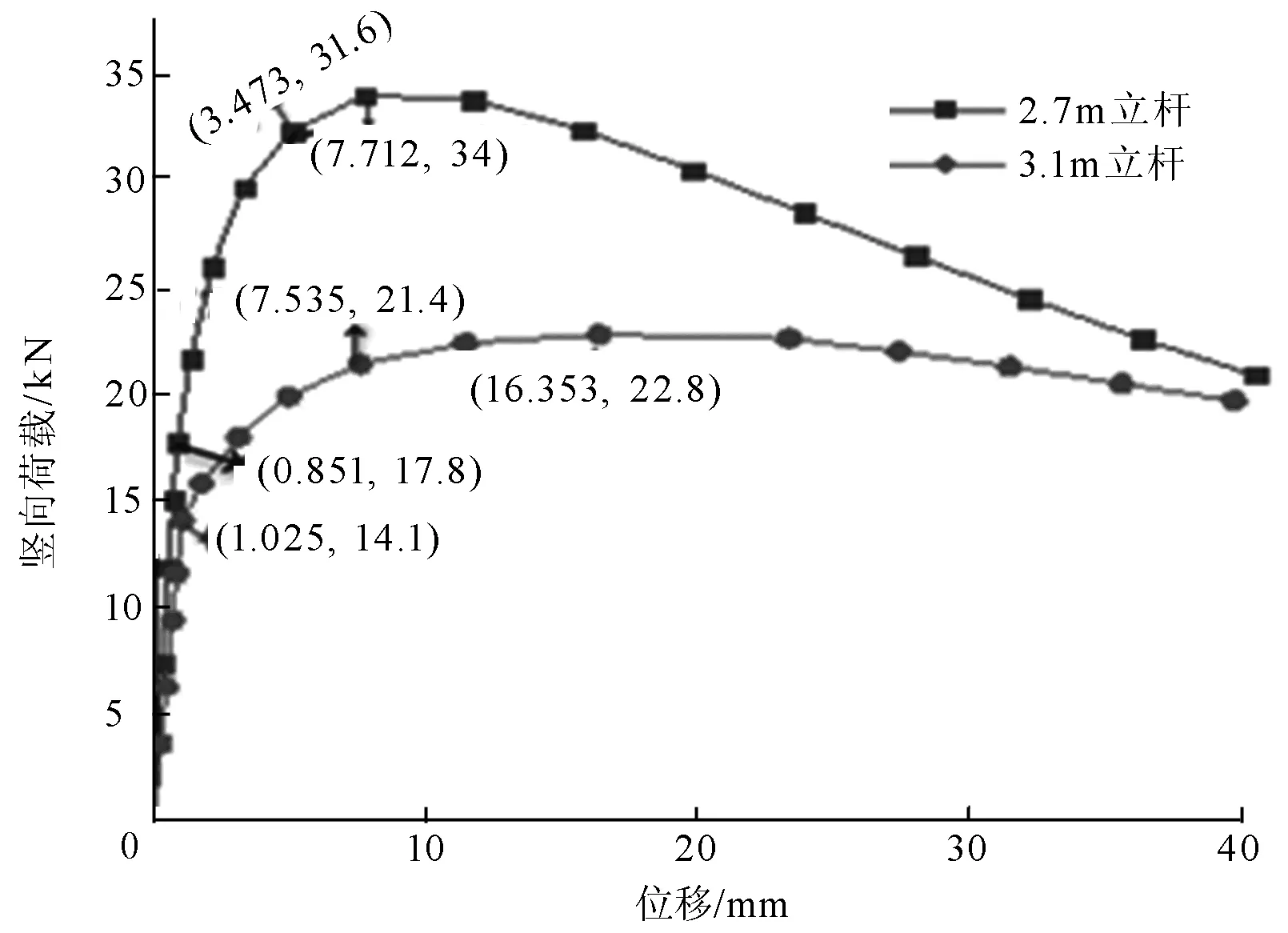
图6 2.7 m和3.1 m立杆位移-荷载模拟曲线

3.3 结果分析

(1)对比图3和图6可知，模拟下的位移变化规律同试验，弹性阶段、弹塑性阶段和破坏阶段的变形值相近，因此试验状态接近理想状态。

(2)17.8 kN(14.1 kN)是立杆弹性变形临界点，此荷载下，立杆各点变形均很小，且呈线性变化，此时立杆能正常工作，随后进入弹塑性阶段32.3 kN(21.4 kN)，极限荷载达到了34 kN(22.8 kN)，此时立杆开始进入破坏阶段。

3.4 承载性能影响因素分析

通过ABAQUS模拟不同因素对立杆承载性能的影响，结果如下：

(1)支撑高度影响：3.3节对2.7 m和3.1 m立杆进行了模拟，由图6的结果可知,两立杆的弹性承载力分别为17.8 kN和14.1 kN，极限承载力分别为34 kN和22.8 kN。高度增加15%，弹性承载力下降了21%，极限承载力下降了33%。因此支撑高度对早拆立杆的承载性能影响显著。

(2)立杆壁厚影响：不同壁厚下立杆的变形如图7所示。

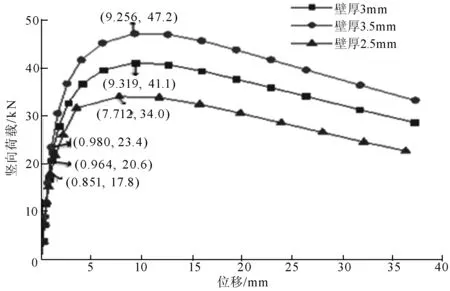
图7 壁厚2.5 m、3 mm和3.5 mm下位移-荷载曲线

由图7可知,立杆的壁厚对承载力的影响是较大的，壁厚每增加0.5 mm，弹性承载力增大15%左右，约3 kN，因此立杆壁厚越厚，承载力越大，现场应进行材料质量控制。

(3)初始偏心影响：施工时，立杆的内外管，在连接部位可能因松动导致立杆的轴线不在一条直线上，由此产生初始偏心，以偏心1/4/、1/2内管直径进行模拟，变形结果如图8所示。

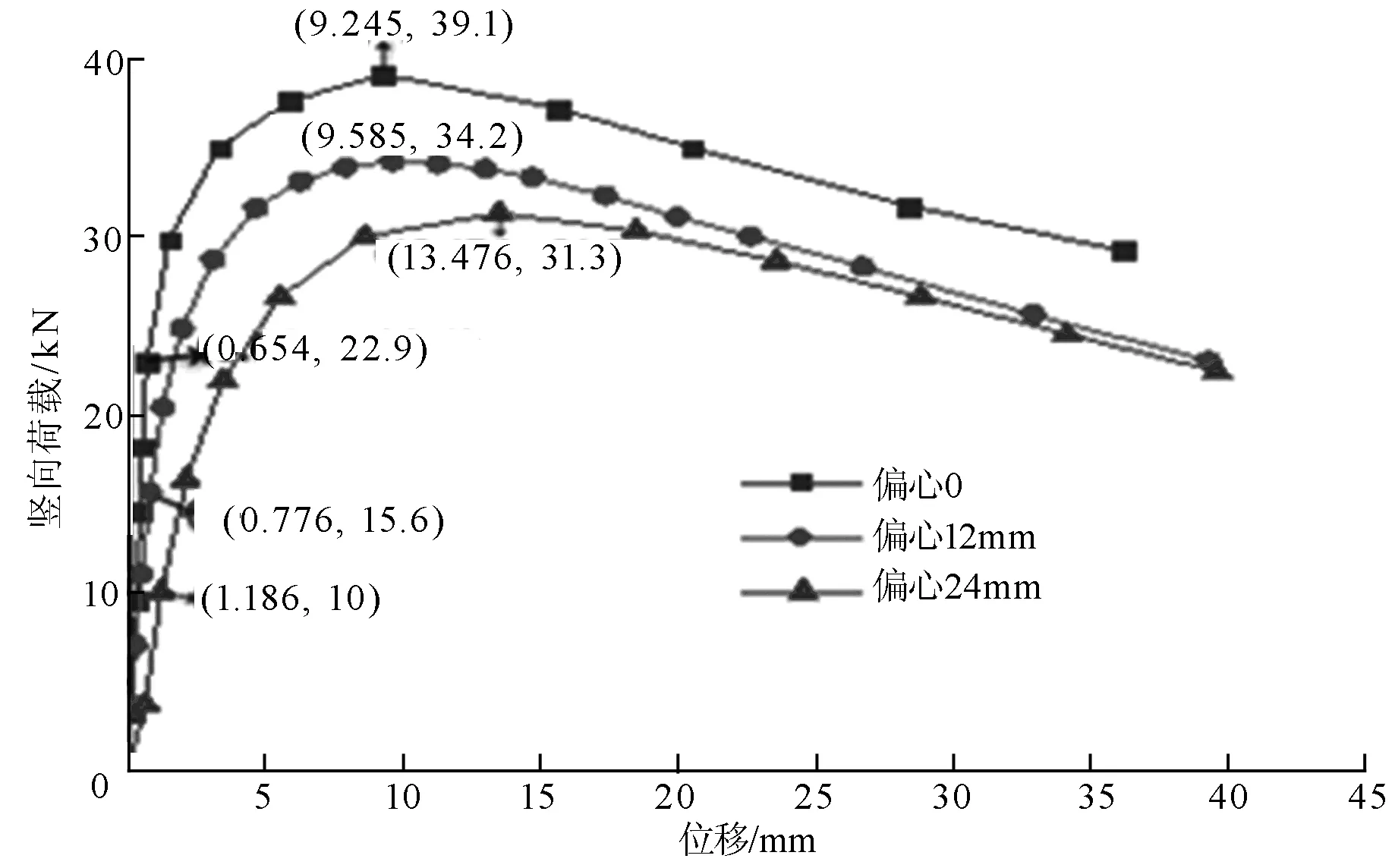
图8 偏心0、12 mm和24 mm下位移-荷载曲线

由图8可知,偏心增加12 mm，弹性承载力降低40%左右，极限荷载也有所降低，弹性阶段变形增大。因此，初始偏心对立杆承载力影响显著：初始偏心越大，立杆的承载力就越小，屈曲变形越大，现场应进行安装质量控制。

4 理论值、试验值、模拟值对比分析

三者的对比见表2，如图9所示(以2.7m立杆为例)。

表2 2.7m立杆理论值、试验值和模拟值对比

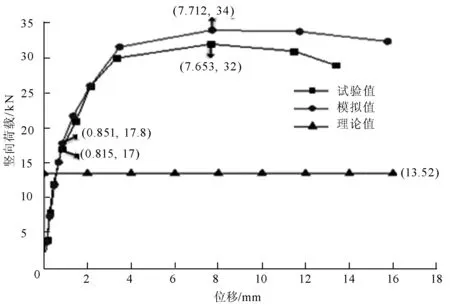
图9 三种结果对比图

由表2分析可知：

(1)竖向荷载下，承载力试验值为17 kN，模拟值为17.8 kN，模拟值与试验值的误差仅为4.7%。现场搭设架体时垂直度会有偏差，一旦搭设误差达到24 mm，承载力直降40%左右，且存在材料质量误差，而试验是理想的，故可将试验状态下的弹性荷载折减70%后作为施工设计值，即为12 kN，而理论承载力为13.52 kN，说明理论值偏高，且距离弹性临界点17 kN较近。

(2)取折减70%作为设计荷载(即12 kN)，离破坏点(32 kN)还有63%，距离弹塑性临界点(30 kN)还剩60%，有很大的安全余量，说明12 kN是合理且安全的。

(3)对比试验下和模拟下立杆的弹性位移可知：两种情况下的弹性变形相差不大，且均为超过0.9 mm，该变形是很小且相对安全的，立杆能正常工作。

5 结束语

通过理论计算、试验研究、模拟分析，对早拆立杆的承载性能进行了研究，主要有以下几点结论：

(1)对于φ60×2.2套管套住φ48×2.5插管的2.7 m(3.1 m)立杆，建议施工承载力设计值为12 kN(9 kN)。

(2)立杆的高度、壁厚、初始偏心等因素对立杆的承载力和稳定性有显著影响，施工时应严格控制：立杆规格应严格按照设计方案布置，立杆垂直度应控制在层高的1/300以内。

(3)在施工技术上，应对施工人员进行规范操作技术的培训，提高施工水平。