一种全局优化的激光光斑亚像素定中算法
2020-06-07徐尤南高文海宋小科余昌鑫
徐尤南,高文海,宋小科,余昌鑫
(华东交通大学机电与车辆工程学院,江西 南昌 330013)
1 引 言
在盾构导向系统中,激光靶测量法用于测量盾构机姿态角,其原理是通过图像预处理和定中算法确定激光靶在CCD上形成激光光斑中心位置[1]。这一方法同样适用TBM姿态角的测量。据调查掘进机(包括盾构和TBM)的姿态误差控制极限值为30 mm/m,而激光光斑直径达2 mm左右。显然,其定中精度对姿态测量误差控制有较大影响,另一方面,激光光斑定中算法的速度还对掘进机姿态进行适时反馈控制有直接影响。因此,如何提高激光光斑定中精度及其算法效率,对掘进机姿态的测量与控制具有实际研究意义。
目前,激光光斑中心位置定中算法主要有质心法、Hough变换法、圆拟合法、高斯曲面拟合法等[2-5]。这些方法,虽然在一定范围内满足了各类光学测量场合中高精度光斑定位要求,但是也存在某些方面局限。如:质心法和圆拟合法计算速度快,但抗噪能力弱;Hough变换法在光斑边缘较清晰时精度高,但耗时较长,易受干扰;高斯拟合法精度较高,但算法复杂,运算量大。
近年来,在激光制导、通信等领域,对激光光斑中心的检测要求不断提高,涌现了一些定位精度高,抗干扰性强的激光光斑定中算法,如加权插值法[6]、阈值分割法[7]等。其特点是以半导体激光器作为发光点,尽管在介质中传播时受到各种干扰,但其在CCD表面形成的激光光斑的能量依然可以看作以中心对称的高斯分布[8]。加权插值法对高斯光斑图像内所有有效像元分组插值计算,对结果加权平均处理,使得定位精度达到0.01 pixels,同时提高了结果的稳定性,但容易受到内饱和的影响。阈值分割法则是改进Ostu阈值分割方法,使得对高斯噪声和湍流影响抗干扰性有明显提高,光斑定位精度得以提高,但同时也增加了原算法的计算量。
针对现有激光光斑的定中算法的不足,本文提出一种基于距离加权的激光光斑定中算法,旨在提高其算法的精度、稳定性与效率。拟通过人工光斑仿真分析算法的定中精度及其效率,通过不同噪声水平下定中分析检验所述算法的稳定性和抗干扰能力,通过对实测激光光斑进行定中,检验该算法的有效性和实用性。所述算法,将为掘进机姿态测量精度和效率的提高提供参考。下面将从等效激光光斑模型的建立、评价指标和中心定位算法、仿真分析与实验等方面对所述算法加以介绍。
2 等效激光光斑模型建立
理论上,单色激光照射到CCD表面上后,会形成一幅光斑灰度图,且其光强等值线图为一族同心圆,为方便叙述,将该圆称为投影圆(图1)。基于这一假设,与其激光光斑中心点C距离相等的点处的光强处处相等。据此,可建立识别其中心点C的等效物理模型。假定待识别的光斑中心点为P,以该点为参考点,在光斑图像所在平面建立如图2所示的笛卡尔坐标系P-uv,Ci为等效光斑上的投影圆,其上任意一点Q(r,θ),r为极坐标的半径,θ为极坐标的极角,其对应的笛卡尔坐标为Q(u,v)。

图1 单色激光光斑灰度图Fig.1 Monochromatic laser spot

图2 等效光斑物理模型Fig.2 Equivalent physical model of laser spot
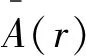
(1)
与传统的圆投影计算中采用Bresenham算法离散数字圆相比[9],本文采用一种整数圆离散,并根据等效光强原理,利用相邻的两投影圆内的整点,估计该投影圆上期望值,称为整数圆投影。为计算方便,先对整点至与其相邻的两个整数投影圆间的距离进行定义:
(2)
式中,[r]为r(u,v)的向下取整值;λ(r),μ(r)分别为Q(u,v)点至相邻两个投影圆的距离;其半径分别为[r]及[r]+1。由此可得,整数圆投影上光强的等效值为:
(3)
有了整数圆投影光强之后,即可对激光光斑进行重建。显然,对于正好落在投影圆上的整点,其重建后的光强即为投影圆上的光强。显然,仅有少数整点将落在投影圆上,为此,对于不在投影圆上的整点的光强需要根据相邻的两个整数投影圆的等效光强来估计,其计算式为:

(4)

下面将根据所建立的等效光斑模型与原光斑模型的差异,来建立识别P点是否为激光光斑中心的评价指标。
3 激光光斑中心定位
为建立识别P点是否为激光光斑中心的评价指标,有必要对等效光斑的特征进行简要分析。显然,如若P恰好位于C点,则所建立的等效光斑将于原光斑相同,如若P与C点有位置偏差,则所建立的等效光斑将于原光斑产生一定的差异。如若两者距离较近,则其等效光斑将比原光斑略大,但光强略小(图2);如若两者距离较大,则其等效光斑将出现中心及外侧较暗的光环(图3)。根据这一特征,可以根据等效光斑最大光强、等效光斑大小、等效光斑光强沿径向分布来识别P点是否为光斑中心。

图3 等效光斑Fig.3 Equivalent laser spot
上述方法,未考虑重建光斑与原光斑光强的具体分布差异,且有多个参数,评价不便。为此,定义识别点P与真实点C的距离指标PDI(Points Distance Index):
(5)
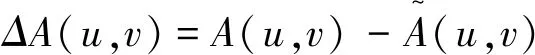
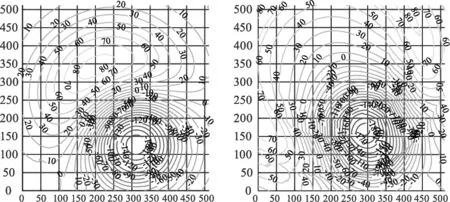
图4 等效光斑与原光斑的光强差Fig.4 The Intensity difference between equivalent spot and original spot
图4可以看出,如若P恰好位于C点,则所建立的等效光斑将于原光斑相同,PDI1=0。如若P与C点有位置偏差,则所建立的等效光斑将于原光斑产生一定的差异,PDI1≠0。这与之前的假定一致。
3.1 等效光斑评价指标确定
为考察上述评价指标的科学性,不失一般性,对如图5所示的理想高斯光斑进行分析。该光斑大小为255×255为像素,中心点处于图像中心位置。据式(5)所给出的指标计算结果,在整个区间的分布情况如图6(a)、图6(c)所示(为便于比较,图中计算结果做了归一化处理)。图中注意到,虽然光斑中心为其全局最有点,但其同时还存在四个局部最优点,使得运用优化工具搜索时,有可能得到局部最优,而非全局最优。
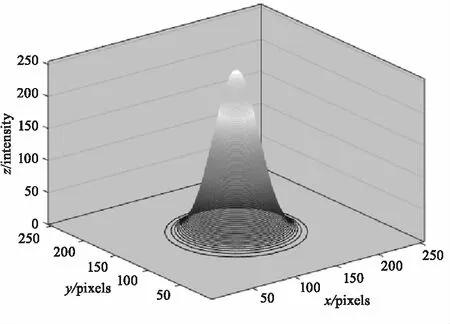
图5 理想高斯光斑三维模型Fig.5 3D model of ideal Gauss spot
为提高指标对误差的敏感性,分别对以下指标进行了试探,结果如图6所示。
(6)
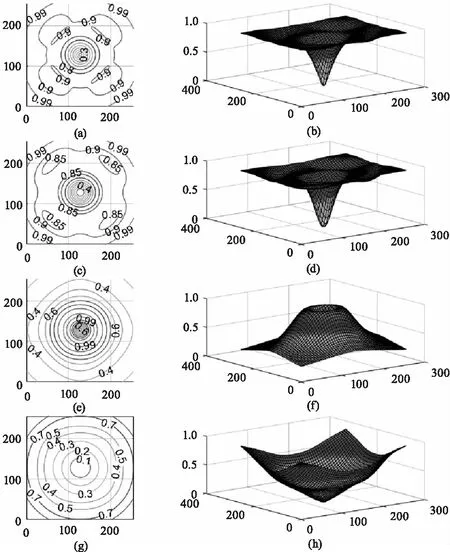
图6 各类指标分布图Fig.6 Distribution map of various index
图中可知,光强偏差平方和指标(PDI2)与光强绝对值之和指标(PDI1)相比,虽然其局部最优点的值更大,距离中心更远,更容易识别,但其分布规律基本相同,不能消除其缺点(图6(c)、(d))。采用光强绝对值反距离加权之和指标(PDI3)与光强绝对值之和指标(PDI1)相比,其共有无穷多个全局最优点分布在光斑四周,其光斑中心则为局部最优点,虽其识别更为容易,但仍然不能消除指标PDI1的缺点(图6(e)、(f))。
采用光强绝对值距离加权之和指标(PDI4)与光强绝对值之和指标(PDI1)相比,只有光斑中心处一个最优点,且其等值线呈圆形(图6(g)、(h)),因此,用优化算法搜索其最优点时,其算法将极为快速稳定。其原理在于,对于CCD采集的光斑图像,由于激光光斑基本服从高斯分布,在±3σ以外范围的像元影响几乎为零,而越靠近中心的像元贡献越大,相反越远离待测光斑中心的光强偏差值影响越大。另外,通过整数投影圆的期望值有利与排除一部分噪声的干扰。
综上所述,本文采用距离加权的圆度偏差作为本文定中算法的评价指标,用于激光光斑的中心识别的表达式为:
(7)
式中,PDI为给定待识别中心P采用光强绝对值距离加权之和指标。
在全域范围内,如若Q=0,则表示已找到绝对的光强中心C;如若Q≠0,则表示所述搜索点O与绝对光强中心C还有一定偏差。该式,利用距离抑加权法制了噪声干扰对算法精度的影响。
3.2 光斑中心全局优化方法
为了找到激光光斑中心C,本文拟采用非线性问题的最优化算法,搜索C(x,y)的位置,确定目标函数为该加权值之和Q。
根据最优化理论,当目标函数F值最小时,所得解即为中心点坐标(x,y),因此其优化检测模型如下,
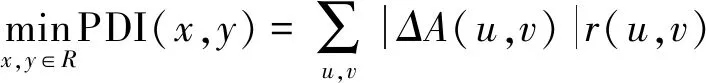
s.t.
(8)
如图7所示的是目标函数PDI归一化后随偏移距离d变化的关系曲线,其中偏移距离d为搜索点坐标至真实坐标中心(x0,y0)的像素距离值。
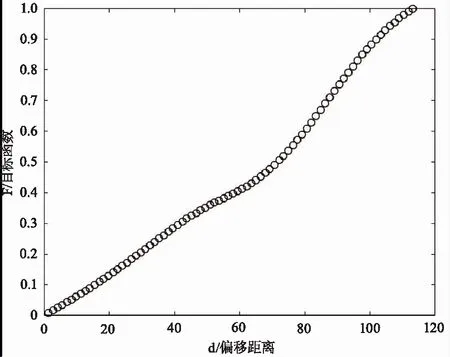
图7 目标函数-偏置距离关系曲线图Fig.7 Object function-bias distance relation curve
可以看出,当偏移距离d在全局范围内,目标函数PDI是d的增函数,此时搜索中心为(x0,y0)时,目标函数最小。
经上述处理,激光光斑的中心定位等效为带边界约束的二元非线性最优化问题,本文采用常规的单纯形优化算法求解。
4 仿真计算
图5是服从高斯分布的理想激光光斑三维模型,从中可以看出激光光斑具有中心圆对称的分布特点。图8为不同噪声水平的模拟激光光斑图像,其中光斑大小为255×255像素,理论中心点坐标(128,128),当方差为0.05时,在高斯噪声的干扰下,光斑图像的中心已变得非常模糊,贴近实际光斑图像。

图8 不同噪声下光斑仿真图Fig.8 Spot simulation under different noises
4.1 定中精度
在无任何噪声情况下,给定不同初始中心点,该算法所得定中结果如表1所示。表中可以看出,所述算法的收敛效果良好,且收敛范围广。经统计,定中结果随着估计中心的偏移距离越小定中精度越高,且偏移距离d在光斑范围内,x和y轴方向极限误差绝对值均优于1.0×10-4(保留至小数点后四位),最大定中误差为0.0002,定中误差的标准差为0.0001,该方法可以实现亚像素级定位精度。

表1 不同初始估计中心定中结果Tab.1 Center of laser spot determined by different initial point
4.2 稳定性和抗干扰性
如表2所示,添加不同水平的噪声模拟实际激光光斑,分别为常见的高斯噪声、椒盐噪声以及随机噪声,每个样本容量为1000。其中高斯噪声均值为0,方差则分为0.005、0.02和0.05等三个水平;椒盐噪声密度为0.02;随机噪声均值为0,方差为0.2。
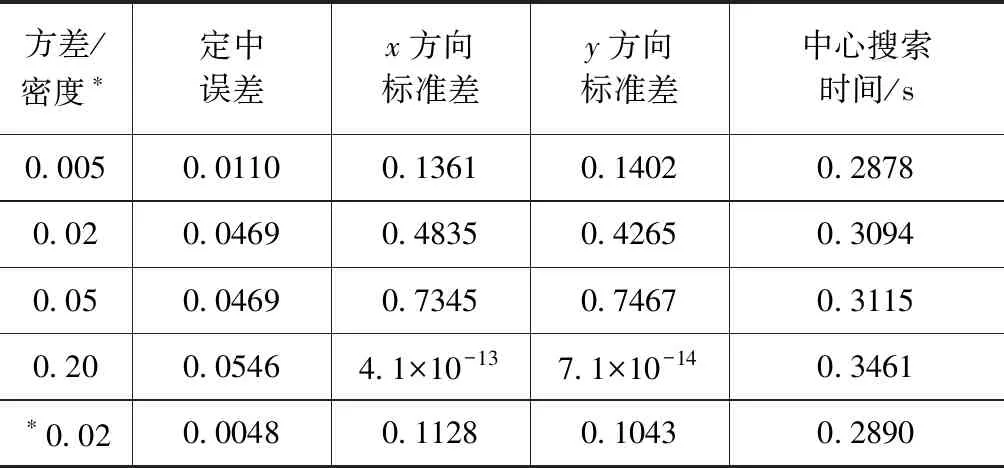
表2 不同噪声水平下的仿真结果Tab.2 Statistical results corresponding to different noise level
表中可以看出,在均值为0,方差为0.05的高斯噪声水平下,该算法定中结果依然保持较小的定中误差和标准差,且中心搜索时间小于0.35 s,基本满足激光光斑亚像素级定位要求。
5 实验验证
利用CCD采集激光光斑图像经图像处理为二值化图像,如图9所示。通过比较质心法和该算法的定中结果,可以看出光斑的中心不在质心处(标记*),这是由于大气湍流,各种光学噪声等因素,造成实际光斑光强不再严格服从高斯分布[10]。点1为初始估计中心(185.5,210.54),点2为本文算法定中坐标(193.3370,202.8271)。

图9 光斑中心检测结果Fig.9 Spot center detection results
给出不同估计初始中心,该算法检测到的光斑中心和最优化目标函数值,如表3所示,可以看出,该算法具有较好的定位精度,稳定性。定中结果均近似等于平均值(193.3366,202.8267)。该算法在检测中心处的目标函数值为3.59×108,对不同偏移距离的初始估计中心收敛。若要进一步优化定中精度,在不改变光斑中心的情况下,可以对光斑图像进行高斯滤波预处理。
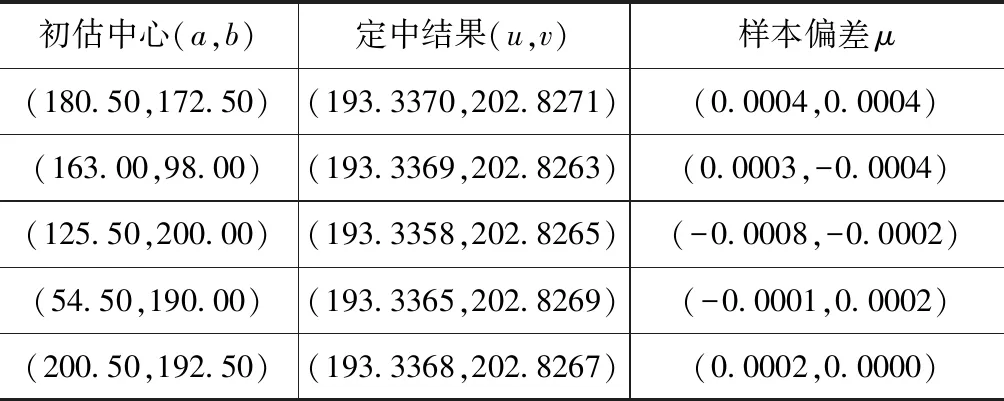
表3 不同估计初始中心检测结果Tab.3 Detection results of initial centers with different estimates
6 结 论
本文根据激光光斑光强服从高斯分布和圆对称的特点,提出了一种基于整数圆投影的全局优化中心定位算法。该法首先通过估计中心点重建等效光斑,使得整数圆光强为期望均值,计算差分图像的圆投影绝对值;接着构建了若干种圆度偏差指标,并确立了圆度偏差的距离加权之和作为最终评价指标;然后,以所述评价指标为优化目标,建立了最优化数学模型,根据目标函数最小值确定光斑中心点。所述方法具备其他算法所没有的全局收敛能力,仿真和实验结果表明,该算法能从含有大量噪声的光斑图像中找到激光中心,具备小于0.1 pixels的亚像素级定中精度,可靠的稳定性和较快检测速度,能满足盾构导向系统中激光光斑定中要求。该算法也可用于类似的具有圆对称特征的光斑图像中心检测,且可以与其他方法融合,通过两步法定中,以进一步提高算法效率。
