基于Fisher准则的Otsu法在光斑中心定位中的应用
2020-06-07张明富段梦琨马月辉
张明富,段梦琨,马月辉
(石家庄铁道大学电气与电子工程学院,河北 石家庄 050011)
1 引 言
基于视觉的形变量测系统主要包括被测物、图像采集设备和计算机等部分。CCD器件兼顾高精度与非接触性等优点,故其广泛应用于形变量测系统的图像数据采集部分[1]。而激光光斑具有传输距离远、受环境影响小,亮度集中等特性,大多数的形变量测都采用激光光斑作为被测物体,因此实现高精度的光斑定位具有十分重要的意义。
现有的光斑定位算法有圆拟合法[2]、Hough变换法[3]、灰度质心法[4]以及多种改进算法。圆拟合法时间复杂度较小,运算精度高,而且算法运算速度快。但在实测中,噪声的干扰会使圆拟合的应用受到一定限制。Hough检测法应用较多,该方法对光斑图像质量要求较低,对噪声以及光斑残缺具有较好的鲁棒性。但其在进行光斑定位时需对参数空间离散化,计算量较大。并且该方法逐点投票、记录结果未必唯一,不同点得到的图像空间曲线差异较大,由此可引入定位误差;灰度质心法对于均匀光斑能够精确定位,计算速度快,但抗噪能力差。对于直接光斑定位中存在的噪声干扰,徐亚明[5]、郭玉静[6]等人提出对光斑图像先分割再定位,可有效抑制干扰。赵琦[7]等人通过改进的Otus法对含噪光斑图像进行阈值分割,再进行光斑质心定位,与传统Otsu阈值分割相比其定位误差降低了25 %以上。对光斑图像进行阈值分割可减少噪声对光斑定位的影响,但光斑图像的分割属于小目标分割,其特点是目标与背景的大小之比通常很小,采用Otsu法进行光斑分割,将背景划为目标一部分可能得到更大的类间方差,导致在分割中引进误差,进而影响光斑定位效果。
基于以上原因,本文采用先分割后定位进行光斑质心检测,且考虑到光斑与背景具有灰度值相差较大,在准确分割后光斑和背景内部灰度均匀,类内方差很小,类间方差很大等特点,符合Fisher准则函数与Otsu法各自优点。基于此,本文提出了一种通过改进阈值分割来消除光斑中存在的噪声干扰。通过将Fisher准则函数应用于Otsu法可有效分割目标背景之比较小的光斑图像,消除噪声干扰并减少运算量,在解决噪声对质心法影响的同时,又利用质心法高运算效率,使定位结果兼顾实时性与高精度。
2 传统的阈值选取方法
2.1 阈值法简介
阈值法[8]是一种简单高效的图像分割方法。通过选取阈值将图像分为目标和背景两大类。其数学描述如下:
假设一幅M×N灰度图像I=f(x,y)其灰度值取值范围I={0,1,…,L-1}设T∈I为分割阈值,B={b0,b1}代表二值灰度级,且b0,b1∈I。于是图像函数I=f(x,y)在T上的分割结果可表示为:
(1)
阈值分割实质就是按照某种准则函数求最优阈值T的过程。
2.2 最大类间方差法(Otsu)
最大类间方差法[9](Otsu)法是一种简单高效的分割算法,其基本思想是:选取的阈值应使目标和背景两类对象间具有最好的分离度,其判断准则为目标背景两类之间方差最大。
设一幅大小M×N灰度图I=f(x,y)灰度级为L,其灰度为i的像素个数为ni其中i∈{0,1,2,…,L-1},用阈值T将其分为两组C0={0~T-1}背景(暗),C1={T~L-1}为目标(亮)。
像素总数:
(2)
各灰度值概率:
(3)
图像平均灰度为:
(4)
在阈值T下背景和目标的像素概率为ω0和ω1:
(5)
(6)
在阈值T下背景和目标的平均灰度为μ0和μ1:
(7)
(8)
图像的类间方差为:
σ2(T)=ω0(μ0-μ)2+ω1(μ1-μ)2
=ω0ω1(μ1-μ0)2
(9)
对于目标较大,且无噪声干扰图像,Otsu法可准确高效将目标从背景分离。但对光斑图像的分割属于小目标分割,通常光斑在整幅图像中面积比远小于0.1,现假设存在最优阈值T可准确分割光斑,则有:
ω1≪0.5<ω0
(10)
将式(9)Otsu准则公式更改为:
σ2(T)=p1p0
(11)
式中:
p1=ω0ω1=(1-ω1)ω1
(12)
p0=(μ1-μ0)2
(13)
当ω1取0.5时p1取最大值0.25,因为ω1≪0.5可知p1≪0.25。当阈值t从最优阈值T开始递减将使ω1迅速增加,p1亦迅速增加。但μ1,μ0作为平均灰度变化缓慢使得p0变化缓慢,此时可使σ2(T)小于σ2(t),即将背景划分为目标一部分,由此造成错误分割,进而影响光斑定位精度。
3 光斑中心定位算法的改进
3.1 Fisher准则分割法
假设现有N个d维特征向量{X1,X2,…,XN}其中Xi={x1,x2,…,xd},在模式识别中,将其投影到一条直线上,形成一维空间。设d=2,则Xi={X1,X2},由图1可知,对比A、B两类在Y1和Y2两个方向投影,其在Y2上两类不相交且距离较远,因此具有更好的分离度。
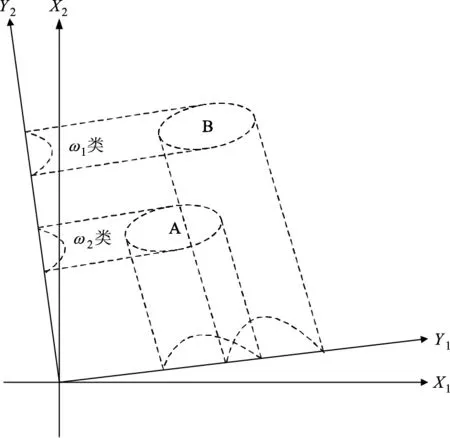
图1 二维特征向量在直线上的投影Fig.1 Projection of two dimensional eigenvectors on a straight line

尊重大学生对传统文化自信培育的多样性,强调自我教育的作用,积极开拓第二课堂,培养自主践行能力,发挥优秀传统文化感染力的作用。我校已持续两年开展“寻找家乡古建和传统工艺”假期调研活动,千余名学生积极参与,利用假期回归故乡,寻找和探索失散在广阔大地的传统文化和背后的故事,开学后进行分享展出。
(14)
式中,
和ω2为X在Y方向上投影后y所属的类别。通过改变Y方向使JF(Y)取最大时,此时Y为最佳投影方向,该方向使A、B两类分离度最好。
由以上推导可知Fisher准则可作为判定类别分离程度的有效依据[11]。在灰度图像中,通过合理的判断准则来选取阈值可使目标和背景达到最佳的分离程度。由于Fisher函数的特性,故可将Fisher函数JF(Y)作为评价阈值分割好坏的准则。
由2.1节Otsu阈值分割可知,各灰度值所占概率为pi,在阈值T下背景和目标的所占比例分别为ω0和ω1,其平均灰度为μ0和μ1。可得背景部分和目标部分的各自类内方差:
(15)
(16)
在进行阈值分割时,由于背景和目标所占比例随灰度阈值变化而改变,故须考虑各自比例ω0和ω1,因此Fisher评价函数应为:
(17)
显然,当J(T)值最大时,目标和背景类内灰度均匀,且两类之间灰度相差最大,被阈值T所划分的目标和背景分离度在该准则下得到最优。故可得基于Fisher函数的阈值选取准则为:
(18)
3.2 阈值分割算法改进
现有的Otsu法执行速度快,分割结果较好。但其只考虑了阈值T下背景和目标的类间方差,没有充分考虑背景和目标内的有用信息。当图像质量较差时,如存在噪声干扰或光斑光晕过大,此时将背景划为目标的一部分可能具有更大的类间方差,由此得到较差的分割结果。针对造成误差的原因,现对阈值判别函数进行改进,将Fisher判别准则应用于传统的一维Otsu阈值分割,在Otsu法充分考虑类间方差的基础上增加约束条件:即图像分割后背景和目标类内差别越小,且两类之间平均灰度值差别越大,此时分割最为合理。综合考虑背景和目标的平均灰度和类内方差对阈值选取的影响,将评价函数改进为:
Q(T)=J(T)σ2(T)
(19)
当Q(T)取最大值时背景和目标分离效果最优,此时的T就是最佳阈值,通过该最佳阈值对光斑进行分割,可有效抑制光斑背景噪声,最终实现快速高精度光斑定位。
3.3 光斑中心定位

图2 光斑中心定位流程
Fig.2 Spot centering process
首先对形变量测系统采集光斑图像进行滤波去噪,然后通过改进的阈值分割消除干扰,获得无干扰光斑图,最后利用质心法进行光斑中心计算。
质心法可以看做以灰度为权值的加权型方法[12],设图像质心为(x0,y0),其计算公式为:

(20)
式中,I(i,j)表示图像中第i行j列像素点灰度值。
4 光斑定位精度分析
4.1 盐噪声影响下光斑定位精度
在光斑采集过程中,由于图像传感器、信号通道、解码处理等所产生的脉冲信号,以盐噪声形式影响光斑定位精度,为研究盐噪声下本文算法鲁棒性,用Matlab生成11幅大小300×300光斑中心为(135,129)的光斑图,添加1500到2500间隔值为100的随机盐噪声,采用现有的Otsu法和本文方法对含盐噪声光斑图进行分割,分割结果经质心法定位后,光斑中心坐标数据如表1所示。
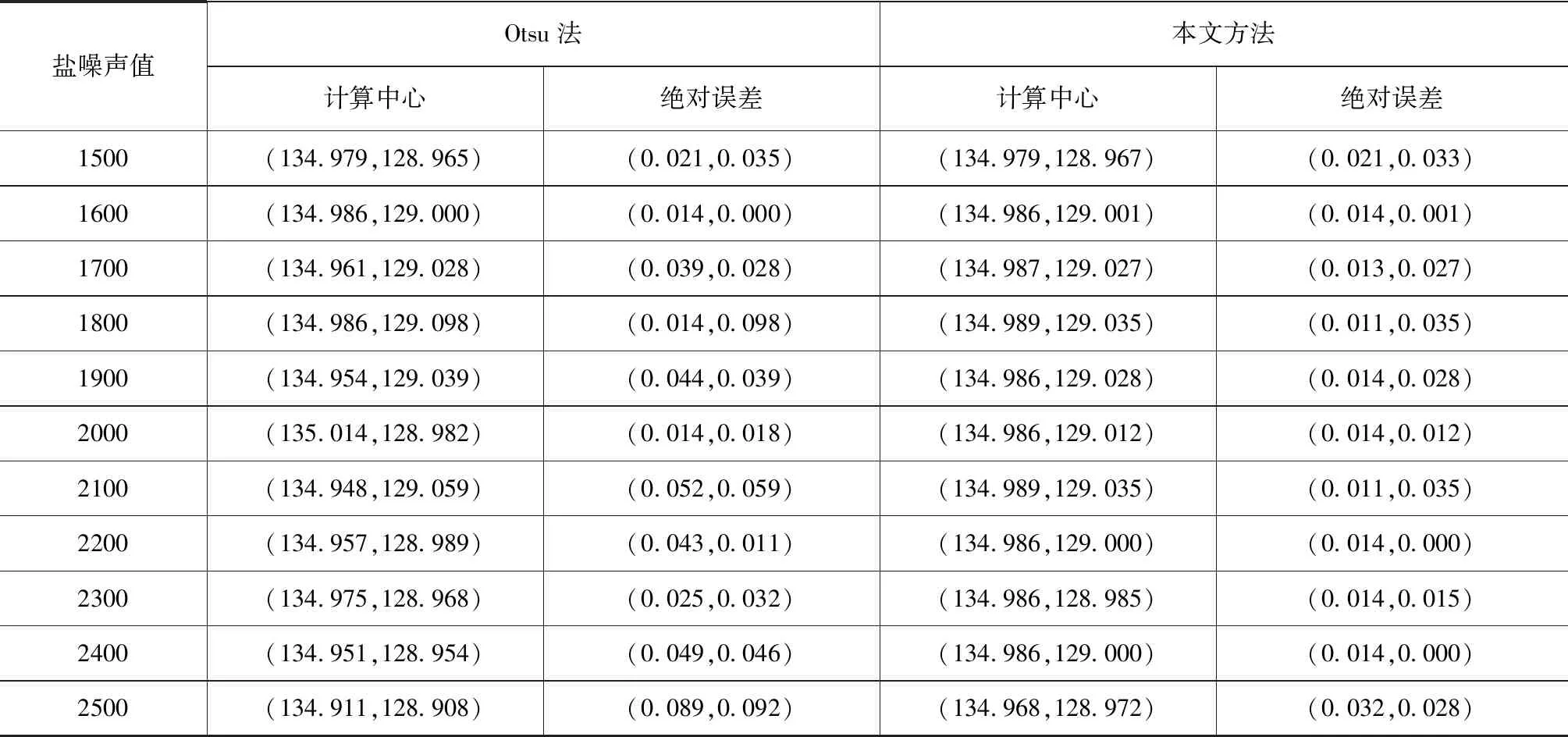
表1 盐噪声下光斑中心定位结果(单位:像素)Tab.1 Location result of spot center under saltnoise(unit:pixel)
分析表中数据可知,随着盐噪声的递增,本文算法分割后所得光斑定位中心较稳定,而采用Otsu法分割后检测到的光斑中心坐标变化较大。利用贝塞尔公式[13]:
(21)
计算检测结果得到的标准差,Otsu法下光斑定位平均误差Otsu法:Δx=0.026,Δy=0.054标准差:σx=0.026,σy=0.054;本文算法Δx=0.016,
Δy=0.019;标准差:σx=0.006,σy=0.02;由此可知:对比两算法定位结果标准差,本文方法具有更好的稳定性。
4.2 高斯噪声影响下光斑定位精度
在4.1节所生成的光斑图像上添加均值为3,方差为3,噪声强度系数从0增至10间隔为1的高斯噪声。采用现有的Otsu法和本文方法对含高斯噪声光斑图进行分割,分割结果经质心法定位后,光斑中心坐标数据如表2所示。

表2 高斯噪声下光斑中心定位结果(单位:像素)Tab.2 Location result of spot center under Gauss noise(unit:pixel)
分析表中数据可知,Otsu法下光斑定位平均误差:Δx=0.059,Δy=0.050;标准差:σx=0.021,σy=0.051;本文算法下光斑定位平均误差:Δx=0.033,Δy=0.030;标准差:σx=0.017,σy=0.037;由此可知:本文算法检测结果标准差较小,且在x方向平均误差降低了44 %,在y方向上平均误差降低了40 %,在兼具稳定性的同时,提到了定位精度。
5 结 论
激光光斑中心检测是基于视觉形变量测系统中的关键技术,本文综合考虑背景和目标灰度区分度以及类内离散度对阈值选取的影响,将平均灰度和类内方差应用于光斑图像的阈值分割中,解决了现有的Otsu法对目标和背景类内像素均匀度以及类间灰度差异利用不足的问题,提高了光斑中心的定位精度。实验表明,在噪声影响下本文方法具有更高的精准度和稳定性,是一种可行的光斑中心定位方法。
