弹体壁厚对模拟弹侵彻能力影响分析

王辰瑞，洪 亮

(南京理工大学 能源与动力工程学院，南京 210094)

现代战争中，大量的攻击目标转入地下或增加了厚重的装甲，如指挥中心、控制中心、战舰、装甲车等，目标打击难度的增加，对穿甲弹的侵彻能力就提出了更高的要求。穿甲弹依靠动能穿甲，因此弹体质量对于其侵彻能力具有决定性的影响，那么在控制弹体直径、长度、质量不变的情况下，弹体壁厚的改变对于弹体侵彻能力具有什么样的影响就需要进一步的讨论。

在此前，国内外很多学者已经对战斗部壁厚对侵彻能力的影响进行了详细的论证研究，如Forrestal[1-2]小组研究了侵彻弹直径对其侵彻能力的影响，陈小伟[3]从力学角度给出了弹丸的无量纲壁厚。吴凯等[4]通过改变弹体头部形状得到的速度衰减曲线论证了弹体头部结构对其侵彻性能的影响。李慧卓等[5]论证了弹体结构对混凝土侵彻弹侵彻深度的影响。王金涛等[6]设计了一种弹头为复合结构的穿甲弹，为弹体结构设计提供了一定的理论依据。吕竹文等[7]针对不同厚度复合装甲进行了抗穿透性分析，对于穿甲弹侵的设计提供了一定的帮助。

综上所述，直接以弹体壁厚为变量的分析计算尚显不足，对弹体壁厚进行分析，增强弹体的侵彻能力，对于未来破坏厚重装甲的作战任务是必要的。本文主要利用LS-DYNA软件对侵彻过程进行仿真，结合现场试验结果，验证弹体壁厚对平头弹侵彻能力影响的变化规律。

1 物理模型及数值仿真

1.1 数值模拟方法与物理模型

数值仿真分析法中的有限元法是研究侵彻问题时使用较多的方法。该方法先将连续求解域离散化为有限个单元，利用计算机通过数值计算方法求得问题的近似解[8-9]。拉格朗日法是弹丸侵彻金属靶板的常用方法，该网格连接在弹丸和靶板的刚性材料上，随着弹丸和靶板的侵彻和挤压，单元网格发生变形。在网格形变量较大时，拉格朗日方法容易产生负体积，导致计算错误。

两种弹芯直径、长度相同，为保证总质量不变，控制弹体壁厚为变量，通过改变内部塑料假药密度，调节内部塑料假药质量，可保证弹体总质量一定。平头弹体结构如图1所示，弹体初速度固定为289 m/s，垂直侵彻金属靶板。本文采用3.6 mm、5.4 mm、6.0 mm、6.6 mm、7.2 mm共五种壁厚模型进行试验及仿真计算。

图1 弹体模型示意图

1.2 仿真模型

为了减少计算量，加快求解速度，本文沿对称平面上建立了四分之一模型。利用Solidworks建立三维实体模型，以iges格式导入hypermesh中划分网格，由于侵彻主要发生于弹丸头部与靶板的接触部分，因此对接触部分的网格进行加密，避免因网格变形严重引起的计算错误，模型如图2。

图2 薄壁弹体1/4有限元模型

将网格文件导入DYNA的前处理软件Prepost中进行算法及边界条件设置，将单元类型设置为solid164实体单元。对于不发生侵彻的假药与弹体外壁之间采用自动的面面接触算法AUOTOMATIC SURFACE TO SURFACE，针对弹丸与目标的接触问题，采用面面接触的侵蚀算法ERODING SURFACE TO SURFACE，在靶板的边界面上施加非反射边界条件NON REFLECTING，侵彻接触控制CONTROL CONTACT的接触刚度取值为侵彻计算时常用的SLSFAC=0.1。弹体及靶板采用Johnson-cook模型[10]，该模型能很好地模拟金属材料间的侵彻破坏。

JC本构方程如下：

(1)

其中，无量纲温度

(2)

断裂失效由下式定义：

[1+D5T*],EFMIN)

(3)

ρ为密度，G为剪切模量，E为杨氏模量，Pr为泊松比，A为屈服应力参数，B为硬化系数，N为硬化指数，C为应变率系数，M为温度系数，Tm为熔化温度，Tr为环境温度，D1～D5为失效参数。

本文靶板材料采用921A钢[11]，失效准则参考李继承等的计算方法，采用最大失效应变作为单元失效准则，取D1=1.13，弹体材料采用30CrMnSi钢，参数见表1、表2。

2 现场试验

试验现场布置如图3所示，借用高速摄像对出膛后的弹体进行拍摄，观察弹体飞行姿态及着靶角度等，通过靶板前设置的测速网靶对弹体着靶速度进行估算。

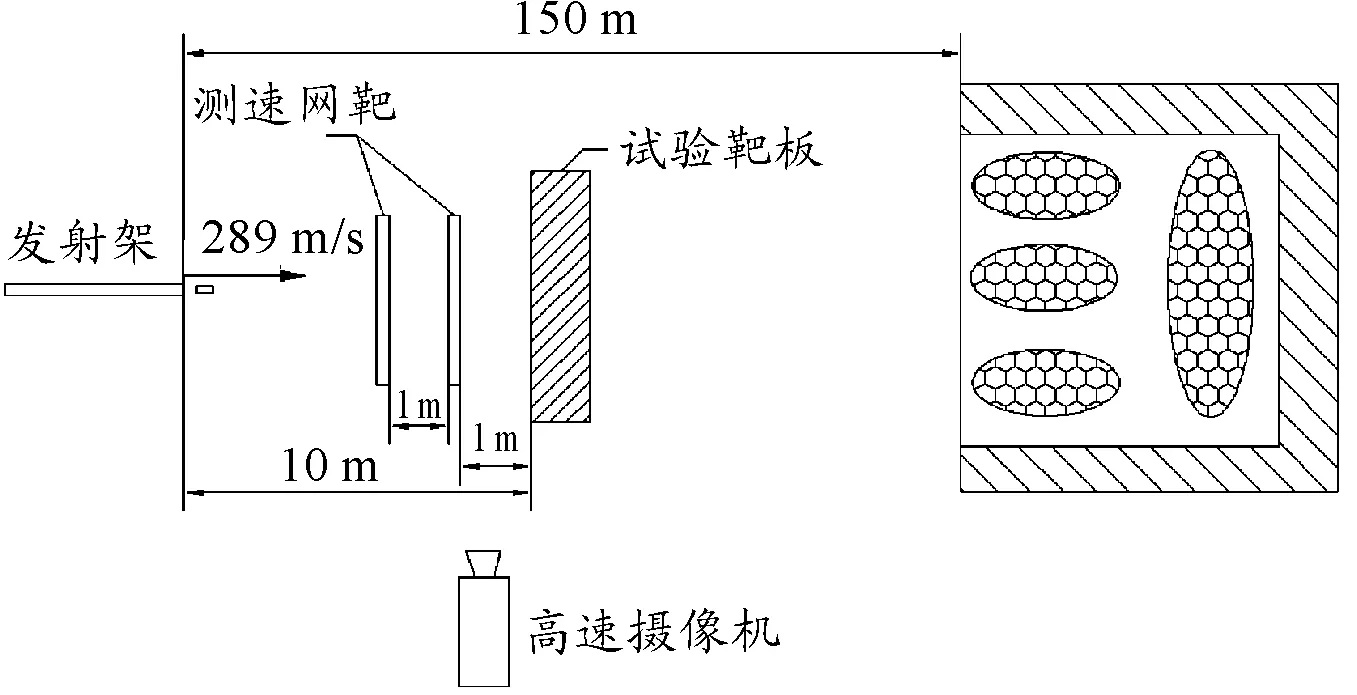
图3 试验现场布置示意图

现场试验结果如表3，不同弹体速度及不同靶板厚度所得靶板破坏情况不同，可以根据靶板的凹陷深度获得较为精确的参考数据，与仿真结果进行拟合对比。3号靶板及7号靶板的破坏情况如图4所示，可见弹体壁厚不足时侵彻效果较弱，在靶板中央撞出圆形凹坑，弹体壁厚增大时击穿靶板留下圆形穿孔，靶板整体凹陷变形。

表1 靶板材料921A钢

表2 弹体材料30CrMnSi钢

表3 现场试验情况

3 结果分析

不同壁厚仿真弹芯以289 m/s速度分别侵彻18 mm、20 mm的金属靶板，仿真结果如图5所示。

靶板凹陷深度可视为在撞击结束、靶板震动停止后靶板内侧的位移。如图6所示，3.6 mm壁厚薄壁弹体侵彻靶板的靶板位移曲线可看出，286 m/s初速时靶板凹陷约为54 mm，328 m/s初速时靶板凹陷约为71 mm，两种情况下的凹陷深度与现场试验情况的51.2 mm、65 mm基本符合，参考图7中5.4 mm壁厚弹体的速度曲线，余速分别为10 m/s左右和53 m/s左右，与现场的7 m/s和49 m/s基本符合，因此可认为仿真结果与试验情况基本符合，材料参数及失效参数可较好的模拟实际情况，拟采用此参数进行下述仿真分析。

图6 3.6 mm壁厚弹体侵彻20 mm靶板靶板位移曲线

图7 5.4 mm壁厚弹体侵彻靶板弹体速度曲线

仿真计算得出，不同弹体在侵彻靶板时的速度变化如图8、图9所示，从图中可以看出，总质量相同的弹体，穿透靶板后的剩余速度并不相同，明显弹体壁厚越厚，剩余速度越高，且速度差几乎等距，因此对剩余速度和弹体壁厚的关系进行直线拟合，得到结果如图10所示。

图8 侵彻18 mm靶板不同壁厚弹体速度曲线

图9 侵彻20 mm靶板不同壁厚弹体速度曲线

图10 弹体壁厚-穿透余速拟合曲线

从图10中可以看出，弹体壁厚与穿透余速之间几乎成线性相关，弹体壁厚增加，穿透余速也随之增加，由此可得出，弹体壁厚对于侵彻能力有影响，侵彻能力随弹体壁厚的增加而线性增长。

4 结论

在控制弹体质量、长度、直径等变量的情况下，仅改变弹体的金属壁厚，会对弹体的穿透能力产生影响，弹体壁厚越厚，穿透能力越强。