基于荷载传递法的单桩沉降简化计算方法
2020-06-06龙秋亮雷皓程
龙秋亮,雷皓程
(1.湖南路桥建设集团有限责任公司,湖南 长沙 410007; 2.中南大学 土木工程学院)
1 引言
针对轴向荷载下单桩沉降计算分析,科研人员进行了大量理论分析、模型试验与现场试验研究。目前主要通过5种方法计算单桩沉降:① 荷载传递法。该方法首先将桩根据桩长、土层分布及精度要求等离散,在节点处利用弹簧模拟荷载-位移关系,利用t-z弹簧模拟桩侧土荷载位移关系,利用q-z弹簧模拟桩端土荷载位移关系;② 剪切位移法。该方法以桩周土体主要承受由桩-土间剪应力产生的剪切变形且桩-土间不产生剪切位移假定为基础,认为单桩沉降由桩周土剪切变形引起;③ 有限元法。利用数值计算软件进行建模计算,但其建模过程复杂,难以准确定义土体及接触面参数,且建模中往往要对边界条件进行简化;④ 弹性理论法。该方法以弹性半空间体假定为基础,通过集中荷载作用下的Mindlin解,由桩-土位移协调条件建立平衡方程,进而求解桩身受力和位移,但其不能精确考虑土的成层性和非线性特性;⑤ 简化计算方法。
荷载传递法计算思路清晰、过程简便,可根据地基土实际情况选用不同的荷载传递模型,桩侧、桩端荷载传递函数可灵活选取,但应综合考虑地基土的实际情况、计算难易程度及相关参数是否容易获取等因素。传递函数主要通过实测获取和理论推导两种方式建立:① 通过现场实测数据拟合;② 根据一定工程经验结合地基土物理力学性质,探求具有广泛适用性的理论传递函数。在模拟桩侧土荷载-位移关系中,双曲线模型应用较广泛,但不易得出解析解,故该文采用与双曲线模型较为接近的内接三折线模型作为侧阻模型,其精度较高且同样可以模拟侧阻应变软化等特点。端阻双曲线模型较侧阻双曲线模型简单,故该文仍采用双曲线模型模拟端阻荷载-位移关系。
采用三折线软化模型模拟桩侧阻力-桩土相对位移的非线性关系,采用双曲线模型模拟桩端荷载-位移关系。根据上述桩侧及桩端荷载传递模型,利用递推方法可从桩端位移计算桩顶沉降和桩顶荷载。最后假设一组桩端位移,可绘制桩顶荷载-沉降曲线。实例分析及数值模拟分析表明该文提出的模型及算法合理易行。
2 桩侧荷载传递模型
试验室和现场测试结果表明:当桩周土剪切相对位移增大至极限侧摩阻力对应的极限相对位移后,侧摩阻力将表现出软化特性。因此,应采用能描述桩周土应力软化现象的模型以更好地模拟桩土界面处的荷载-位移关系。为简化计算,该文拟采用双曲线模型的内接三折线作为侧阻荷载-位移传递模型,其计算量小,参数求解容易。如图1所示。
当桩-土相对位移ΔS小于Su1时,桩侧阻力随相对位移线性增加;当ΔS=Su时,桩侧阻力到达极限侧阻力τmax;当Su1<ΔS≤Su2时,侧摩阻力将出现软化特性,其随着相对位移的增大而减小直至残余侧阻τr。桩周土界面侧摩阻力与相对位移的相互关系用分段函数近似表示:

图1 桩侧土侧摩阻力-相对位移曲线
(1)
式中:τmax为极限侧摩阻(kPa);τr为残余侧摩阻(kPa);Su1为极限侧摩阻力对应的极限桩土相对位移(弹性界限位移)(mm);Su2为侧摩阻力刚达到残余侧阻时对应的相对位移(弹塑性界限位移)(mm);λ1为桩侧土初始抗剪刚度系数(kPa/mm);λ2为桩侧土软化抗剪刚度系数(kPa/mm)。
以上6个参数均可通过现场试验实测数据统计分析获得。在缺少现场试桩数据的情况下也可根据经验取值。其中,张乾青对现场实测数据统计分析表明:不同土层中桩侧土弹性界限相对位移Su1=5~25 mm;侧阻软化率τr/τmax=0.83~0.97。
3 桩端荷载传递模型
采用双曲线函数模型以模拟桩端土荷载-位移关系,如图2所示。
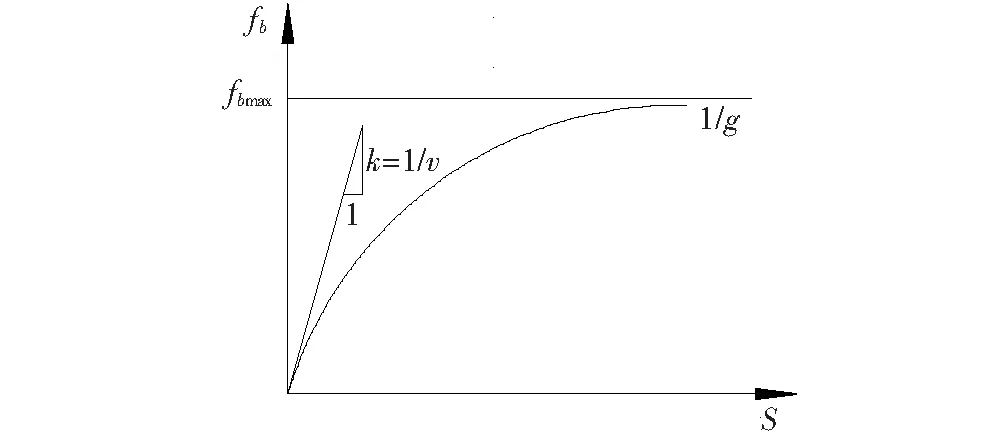
图2 桩端土荷载-位移曲线
该函数模型表达式如下:
(2)
式中:fb(s)为桩端沉降为s时对应的桩端阻值(kPa);s为桩端位移(mm);v、g为经验参数。
(1) 参数v
当Δs=0时,对式(2)求导可得到式(3):
(3)
Randolph和Wroth建议,k的取值可以通过式(4)确定:
(4)
式中:r0为桩身半径(m);vb为桩端土泊松比;Gb为桩端土剪切模量(kPa)。
联立式(3)、(4),可得:
(5)
(2) 参数g
对式(2)在s→+∞时取极限,则桩端极限承载力fbmax可表示为:
(6)
fbmax值受桩端土层特性、桩的形状和桩的形成技术特点等因素影响,故fbmax的值较难确定。目前,确定桩端土极限承载力fbmax方法有多种,如静力触探法、标准贯入法、经验法或参考规范取值,当有现场试桩实测数据时也可通过反分析给出。Randolph提出了一个表达式以估算fbmax的值,该表达式如式(7)所示:
fbmax=PL[1+tanφtan(45°+φ/2)]
(7)
式中:φ为桩端土内摩擦角(°);PL为球孔极限应力(kPa),由式(8)计算:
(8)
式中:c0为黏聚力(kPa);P0为深度z0处原位土应力(kPa)。
联立式(6)、(7)、(8),即可求得参数g。
4 计算方法
基于上述桩侧三折线模型及桩端双曲线模型,该文将通过递推方法由桩端沉降计算单桩桩顶沉降和桩顶荷载。具体计算步骤如下:
(1) 将单桩分为n段(土层底部编号为1,顶部编号为n),且假定侧摩阻力在每个分段中均匀分布,即每个分段中轴力沿桩身方向线性分布。
(2) 任意给定一桩端沉降sb1。
(3) 由式(2)计算单桩第1段下表面荷载Pb1。
(4) 由式(9)计算桩段1总侧阻力:
Ps1=2πr0τ1L/n
(9)
式中:L为单桩桩身长度;n为分段数;r0为桩身半径;τ1为桩身侧阻力,由式(1)计算。
(5) 由式(10)计算桩段1上表面荷载:
Pt1=Pb1+Ps1
(10)
(6) 由式(11)计算桩端1平均轴向力:
(11)
(7) 由式(12)计算桩段1压缩量:
(12)
(8) 由式(13)计算桩段1上表面沉降:
st1=ε1+sb1
(13)
(9) 根据相邻两段轴力和位移的连续性,计算上一段下表面处的轴力和位移:
Pb2=Pt1
(14)
sb2=st1
(15)
式中:下标第一位表示桩段上下表面,其中b为下表面,t为上表面;下标第二位表示桩身分段数。
(10) 重复步骤(4)~(9),直至得到桩顶荷载Ptn和桩顶沉降Stn。
(11) 假设一系列桩端沉降,则可绘制单桩桩顶荷载-沉降曲线。
5 算例验证
茅草街大桥位于湖南省益阳市南县茅草街轮渡口(属湖相洞庭湖软土地区),其桩基础均为钻孔灌注桩。某试桩桩径D=1 m,桩长L=60 m,采用C30混凝土,其混凝土弹性模量实测值为3.47×104MPa。
该文在对试桩荷载-沉降计算分析中,桩侧模型计算参数τmax、Su1均采用文献[15]中的取值;参数τr按0.85τmax取值;参数λ1取Su1与τmax之比值;参数λ2根据经验和实测数据取值;桩端参数v、g由该文式(5)~(8)并参考相应规范计算取值。计算参数及地基土物理力学参数具体取值见表1。最后编制Matlab计算程序进行计算。

表1 茅草街大桥地基土物理力学性质参数
注:桩端参数:v=1/1400 mm/kPa,g=1/6 000 kPa-1。
如图3所示,由该文提出的桩侧、桩端荷载传递模型及计算方法所得的荷载曲线与实测沉降数据拟合良好。当荷载大于6 000 kN时,实测荷载-沉降速率加大,该文计算曲线在6 000 kN附近也表现出此规律;当荷载大于12 000 kN之后,实测荷载沉降速率突然减小,表现异常,可能是在12 000 kN之后,单桩达到极限承载力造成测量误差所致。
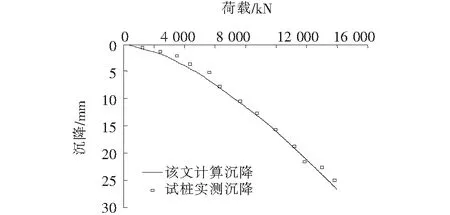
图3 试桩荷载-沉降曲线对比
6 结论
(1) 在深入分析桩土界面非线性接触特性的基础上,考虑桩侧土应变软化特性,采用软化三折线模型模拟桩侧荷载-剪切位移关系,采用双曲线模型模拟桩端土荷载-位移关系,利用递推方法,提出了一种单桩沉降计算的简化方法。
(2) 提出的模型和计算方法能较准确描述地基土的力学性质并有效预测单桩桩顶沉降,该文计算模型较桩侧双曲线模型简单,便于工程设计、施工人员掌握。
