关于半对偶模的两个特殊模类及投射维数
2020-06-06何东林
何东林
(陇南师范高等专科学校 数信学院,甘肃 陇南 742500)
0 引言


1 引理


引理3[4]I(R)⊆CorW(R)且P(R)⊆AcorW(R).
引理4[5]设C是R-模,D是R-模类且对任意D∈D有vD是同构,则以下条件等价:

引理5[5]设C是R-模,D是R-模类且对任意D∈D有uD是同构,则以下条件等价:
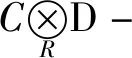
2 主要结论
定理1设M是R-模,则以下条件等价:

证明由引理4、W-余自反模和伴随W-余自反模的定义易证.
定理2设M是R-模,则以下条件等价:
1) 模M具有CorW(R)-预覆盖(CorW(R)-覆盖);
2) 模HomR(W,M)具有AcorW(R)-预覆盖(AcorW(R)-覆盖).
证明由引理5、W-余自反模和伴随W-余自反模的定义可证.
根据引理3及文献[5]中命题2.6可得如下两个推论.
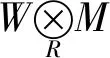
推论2设M是R-模,则M具有满的CorW(R)-覆盖当且仅当M∈CorW(R)且HomR(W,M)具有满的AcorW(R)-预覆盖.
定理3设M是R-模且{M}∪CorW(R)⊆W⊥,则:AcorW(R)-pd(HomR(W,M))≤CorW(R)-pd(M).
证明若CorW(R)-pd(M)=+,则不等式显然成立.若CorW(R)-pd(M)<+,不妨设CorW(R)-pd(M)=n,则由引理2知,存在长度为n的正合列:
(1)

(2)
考虑行正合交换图,如图1.

图1 公式(2)导出交换图
Fig.1 Communicative diagram induced by formula (2)
由图1中上行正合列及Ai∈AcorW(R)知,AcorW(R)-pd(HomR(W,M))≤CorW(R)-pd(M).因此不等式成立.

证明若AcorW(R)-pd(M)=+,则不等式显然成立.若CorW(R)-pd(M)<+,不妨设AcorW(R)-pd(M)=m,则由引理2知,存在长度为m的正合列:
0→HomR(W,Cn)→…→HomR(W,C1)→HomR(W,C0)→M→0,
(3)

(4)

(5)

定理5设M是R-模且{M}∪CorW(R)⊆W⊥,则:AcorW(R)-id(HomR(W,M))≤CorW(R)-id(M).
证明若CorW(R)-id(M)=+,则不等式显然成立.若CorW(R)-id(M)<+,不妨设CorW(R)-pd(M)=n,则由引理2知,存在长度为n的正合列:
(6)
其中Ai∈AcorW(R)(0≤i≤n).因为{M}∪CorW(R)⊆W⊥,所以用函子HomR(W,-)作用于序列(6)可得如下正合列:
(7)


图2 公式(7)导出交换图
Fig.2 Communicative diagram induced by formula (7)
由图2中上行正合列可得,AcorW(R)-id(HomR(W,M))≤CorW(R)-id(M).因此不等式成立.

证明过程与定理5类似.
