基于分布信息直觉模糊c 均值聚类的红外图像分割算法

王晓飞，胡凡奎，黄硕

（黑龙江大学电子工程学院，黑龙江 哈尔滨 150080）

1 引言

无人机遥感的出现及快速发展使遥感科学研究实现从宏观走向微观。利用热红外成像仪发现电力设施故障引起的局部过热现象，再进行人工诊断是如今电网领域广泛普及的主要诊断手段，而无人机遥感具备分辨率高、灵活性强等特点，能高效实时地勘探地面信息，因此红外无人机技术是未来电力设备实时故障诊断的发展方向之一，为国民安全与利益提供技术保障。

红外图像基于物体温度特性的成像原理，使成像环境不受天气或光照条件的限制，在很多领域都拥有着广泛的应用。而随着近年来智能电网概念的提出及不断深入的发展，红外成像技术在设备故障诊断、温度监测等电网领域承担了必不可少的角色，也就使红外成像技术的应用具有重要的民用意义。由于电力设备红外图像中的结构和形状信息对比度不高，红外分割作为目标识别和分析的关键性步骤，其结果将对后续提高识别的精准度起关键性作用。然而，由于红外图像自身性质的限制，很难得到准确的灰度值区分结果。电力设备表面不均匀的散热导致目标的强度分布不均匀；边缘模糊导致的图像分辨率低，纹理细节丢失也是在处理红外图像中常见的现象；此外，变电站作为一个复杂的环境，包括雾雨天气、设备表面反射、非电力设备高强度影响等。基于这些原因，红外电力设备的分割仍然是一个极具挑战性的任务。常规的基于阈值的方法（包括Otsu 方法和最小误差阈值方法）可应用于红外电力设备分割，对红外图像中背景较暗的热目标分割简便高效。然而，当图像包含了复杂的多模态结构后，以上这些传统方法的性能会有明显下降。针对不同直方图的红外图像提出的一种自适应局部双阈值分割方法耗时长，并可能会产生大量的负相关区域。此外，红外图像中存在的非目标物体、边缘模糊、强度不均匀性等都会对以上的方法产生不同程度的影响。

近年来，针对电力设备红外图像分割问题也提出了多种方法。文献[1]提出了一种PCNN（pulse coupled neural network）分割改进算法，将PCNN算法与类内绝对差法结合，通过参数和阈值的优化，对电力设备红外图像进行分割，较好地保留了边缘细节特征。文献[2]提出了一种基于Otsu 算法和区域生长算法结合的分割方法，消除了背景干扰并能准确地提取目标区域。文献[3]使用蝙蝠算法改进了空间信息熵，并快速搜索最优的分割阈值，经阈值分割实验在分割效果和效率上有所提升。文献[4]采用粒子群优化方法的Niblack 对电力设备红外图像进行分割。通过自动搜寻Niblack 中不重叠矩形邻域的最优分割阈值，从设备图像中提取出目标区域。

聚类算法也可用于电力设备红外分割。其中k均值聚类算法作为一种经典聚类方法[5]，计算复杂度低，收敛速度快，但它对噪声的相对敏感度较高，需要图像中不同类的类中心之间的距离要相对较远，而这在红外图像中并不常见。

针对红外图像中目标边缘的不确定性和强度分布的不均匀性，文献[6]利用Atanassov 的直觉模糊集理论对其进行了研究，在处理图像时考虑了隶属度、非隶属度、犹豫度等因素。Pelekis 等[7]进一步提出了数据聚类的直观模糊化，其中数据点xp表示(λp,μ p,νp)而非单个λp，其中，λp表示常数，μ p表示隶属度，νp表示非隶属度。Xu 等[8]将直觉模糊集理论与模糊集理论结合，用直觉模糊距离代替了目标函数中的模糊距离。当中存在的犹豫度为处理数据点的不确定性提供了一种很好的方法。文献[9]将直觉模糊集理论与基于核的模糊c 均值结合起来，利用进化算法选择参数。进化核直觉模糊c 均值聚类算法在噪声干扰条件下性能更稳定，正确率更高。Danish 等[10]提出了一种新的概率相似度度量方法和聚类技术，针对直觉模糊距离设计出自适应权值。然而，图像分割作为一种特殊的分类，所针对的是图像，涉及更多的空间和语义信息。近年来，直觉模糊c 均值（IFCM,intuitionistic fuzzy c-means）聚类算法更多地关注特征点聚类问题，这恰恰决定了在图像具有较强空间相关性的情况下，其分割效果并不太理想。为此，针对变电设备红外图像中存在的强度不均匀性和非高强度目标等问题，本文提出了一种基于局部信息的直觉模糊聚类方法。

本文的主要工作包括以下几点。1) 提出了一种基于引入全局分布信息的模糊聚类算法，该算法针对图像中存在的高强度非电力设备的目标进行分割。在聚类过程中，使用高斯核函数计算目标点到目标质心的空间距离。2) 将局部强度分布信息引入IFCM 中，对距离进行检测，以平衡图像细节与抑制图像强度的不均匀。3) 通过拉格朗日算子法计算目标函数的邻域隶属度，并与传统IFCM 等分割方法进行了对比。

2 直觉模糊聚类算法

2.1 模糊c 均值聚类算法

模糊集理论最早是由Zadeh 在1965 年[11]提出。经过多年的发展，一些扩展的模糊集（如类型2 模糊集[12]、区间类型2 模糊集[13]、直觉模糊集[14]等）被提出，这些扩展的模糊集可以处理更多的不确定性，得到了广泛的应用。1973 年，Dunn 在文献[15]中提出模糊c 均值（FCM,fuzzy c-means）聚类算法，再由Bezdek[16]推广。该算法通过迭代更新隶属度和聚类中心来最小化目标函数J。FCM算法的目标函数定义如式(1)所示，需满足式(2)所示的条件。

其中，U为像素的模糊隶属度矩阵，其行数等于聚类中心数c，列数等于图像像素个数n；xk为第k个数据点；vj为第j类聚类原型；ujk为第k个像素样本对第j个聚类中心的模糊隶属度；m为权重因子；d2(x k vj)为失真度，一般用欧几里得距离表示为

2.2 直觉模糊c 均值算法

2.1 节中所述的FCM 算法的核心理论是将特征函数（其值只能取0 或1）扩展为范围在[ 0,1] 区间内任一值的隶属度函数。但隶属度函数作为一个取值单一的函数，不能表示事物存在的不确定性，也就是说FCM 算法不能准确地描述除了“肯定”与“否定”之外的情况，这种局限性促使了IFCM 算法[14]的诞生。

直觉模糊集（IFS,intuitionistic fuzzy sets）理论提出了犹豫度的概念，该概念表达了带有中立属性的状态，更加完整、精准地描绘了客观现实中存在的模糊信息。n维数据集X可用IFS 表示为

其中，u A(x)和v A(x)分别表示元素x的隶属度和非隶属度，函数u A(x):X→[ 0,1]表示X中元素x绝对属于X的子集A，v A(x):X→[ 0,1]表示X中元素x绝对不属于子集A的程度。在文献[17]中，隶属度和非隶属度的总和应满足0≤u A(x)+v A(x) ≤ 1，因此产生了犹豫度，其作用被定义为

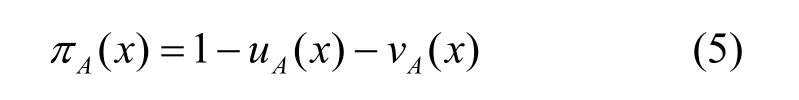
将图像设为I，图像像素为v，灰度值的范围为0～1。根据Vlachos 等[18]的直觉模糊数据理论，将隶属度定义为图像的归一化灰度值，如式(6)所示。

其中，Imax和Imin分别表示图像I的最大灰度值和最小灰度值。Sugeno[17]利用否定函数计算直觉模糊集的非隶属度，如式(7)所示。

其中，λ表示一个值为正的常数，这保证了隶属度和非隶属度的总和不会大于1。

3 电力设备图像分割

通常在实际应用中，电力设备并不是红外图像中唯一的高亮区域，如变电站内的人造建筑、通勤车辆等温度也比较高，因此这些物体在红外图像中呈现出与电力设备相似强度的灰度值，影响了对电力设备的识别。此外，红外图像的强度分布不均匀、边缘模糊，使红外图像的分割更加困难。针对现有电力设备红外图像分割算法的缺陷与不足，本文提出了若干改进措施，主要包括以高斯模型的形式引入全局分布信息；结合局部强度分布信息，将IFCM引入图像分割中。

3.1 基于高斯模型全局分布信息的改进

传统的FCM 算法往往将具有与目标相对强度的像素划分为目标类。由于缺乏全局分布信息，噪声、高灰度值、强度物体等干扰对分割结果影响较大。在式(1)中，对于∀x，隶属度ujk满足，此时，如果m=1，则将FCM 转化为硬c 均值聚类，其隶属值为0 或1。进一步地，如果m≥ 1，为了使目标函数最小化，对于每一个x，较大的权重会将其倾向于分配给较小的。然而，距离度量仅仅指向像素灰度值的强度，这也会导致图像分类出现错误，因为在这个度量标准下，电力设备的像素与其他灰度值相似的像素并没有区别。如图1 所示，电力设备A 点和相似灰度值B 点被FCM 算法划分为同一类。

图1 FCM 分割结果

针对以上问题，将全局分布信息引入FCM 算法的目标函数中。电力设备在图像中可能区域可以用多种方法近似，实际上，只需要一个近似的位置，即包含比图像中电力设备更大的电力设备的区域。这种近似提取的方法耗时为0.25 s 左右，并且分割效果达到标准分割的图像在95%以上，因此考虑时间成本和分割效果，本文采用这种近似位置的电力设备提取方法。

该近似提取的基本前提是，当电力设备的可能区域到质心的距离变短时，像素成为目标的可能性增加。因此，它属于背景的可能性随之降低。模糊聚类中的波动应反映在隶属度上，故通过引入增强隶属度Wjk来适应位置变化，Wjk的分母采用高斯模型，表示像素越靠近质心，越有可能属于目标。当像素位于质心位置时，概率强度曲线达到峰值。如式(8)所示。

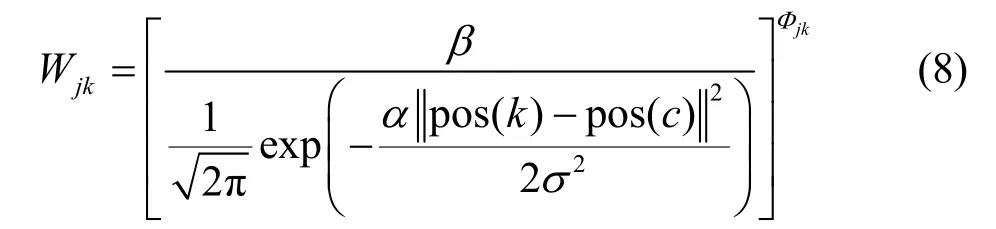
其中，pos(k)为像素k的坐标，pos(c)为电力设备可能区域质心的坐标；α和β为常数，分别为0.75 ×10−3和0.2；σ为方差，一般取3。

FCM、FLICM（fuzzy c-means clustering algorithm based on local information）、IFCM、KIFCM（kernel space intuitionistic fuzzy clustering algorithm）、本文算法等聚类方法得到的A—F 点的第2 类隶属度值如图2 所示。从图2(a)中选取灰度值强度相同的点A—F，其中点A 是离电力设备最近的点，点F是离电力设备最远的点。根据图像中真实的背景信息，只有点A 和点B 属于电力设备，其他的都是非电力设备。由图2(b)可以看出，由于缺乏空间信息，FCM算法和KIFCM算法不同位置点计算出的隶属度值是相同的。在低对比度条件下，不考虑空间信息的分类会造成较高的错误率。KLICM 算法和IFCM算法均受到了局部分布信息的影响，不同位置的点具有不同的隶属度值。同样，在低对比度的情况下，局部分布信息的功能还是有限的。主要原因是局部区域的同质性可能会对聚类产生负面影响，从而导致整个区域保持了同样错误分类的状态。本文所提算法加入全局分布信息后，与其他算法相比，由于不断增加，隶属度会随着与质心距离的增大而逐渐减小，也就获得了较高的精准率，证明了本文所提算法引入全局分布信息的有效性。

图2 相同灰度值强度下电力设备在不同位置点的隶属度值

3.2 基于局部强度分布信息的IFCM 改进算法

红外图像的灰度值强度分布同样不均匀，这是由于物体的表面散热不均匀所造成的，而这种散热的不均匀性会在红外图像中反映出来，这给分割带来了困难，导致有部分电力设备目标图像的边缘缺失与目标划分不准确的问题。如图3 所示，绝缘子部分明显暗于隔离开关，而FCM 算法没有将其划分为目标。

图3 灰度值强度不均匀性图像分割

针对上述问题，本文采用IFCM 算法，结合局部灰度值强度分布信息，改进后的目标函数定义如式(9)和式(10)所示。

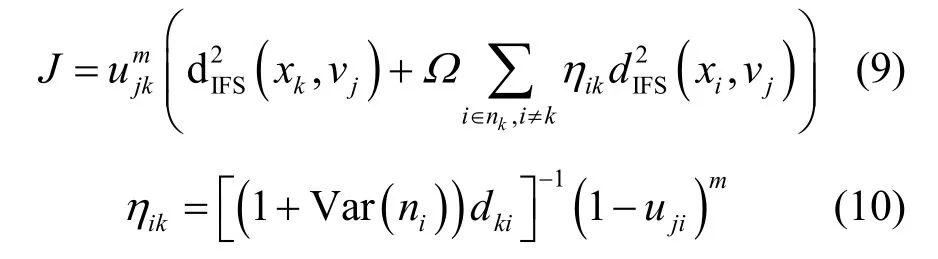
其中，Ω表示控制局部邻近信息的影响，ni表示x的邻域，ηik表示测量xi在xk附近的影响，Var(ni)表示ni的方差，dki表示xi和xk之间的欧几里得空间距离，m表示模糊因子，在该方法中m=2。原始数据只有一个维度，即灰度值，而转换后的数据具有3 个维度，包括u A(x)、v A(x)和πA(x)，因此，聚类质心是一个三维矢量。归一化欧几里得距离度量综合考虑了隶属度、非隶属度和犹豫度来衡量聚类质心与数据点之间的差异。

图4 为FCM 算法、IFCM 算法及引入局部分布信息的IFCM 算法分割结果如图4 所示。与FCM算法相比，引入局部分布信息的IFCM 算法有效地提高了非齐次区域的隶属度，邻域的影响也被控制在适合的边缘、边界和细节范围内。从FCM 算法得到的结果可以看出，被分割后的电力设备并不完整，缺失了绝缘子、电线等。而从IFCM 算法所得到的分割结果与FCM 算法相比显现出更多电力设备目标，但依旧不能完整地将设备目标从背景里分离出来。通过引入局部分布信息的IFCM 算法分割后的结果使电力设备相对于IFCM 算法更加完整，同时也保留了更多电线部分的细节。

3.3 基于分布信息的改进IFCM 的形式

基于上述改进，本文给出了基于分布信息的改进IFCM 的目标函数，如式(11)所示。

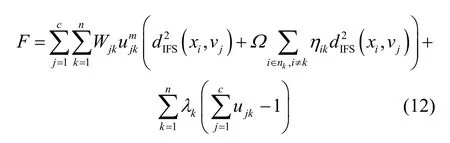
图4 不同算法的图像分割结果

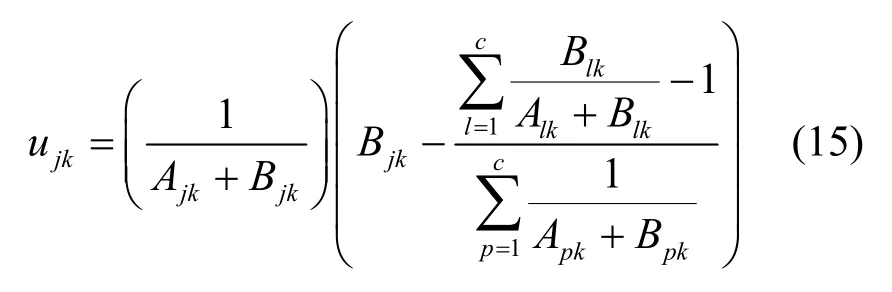
在本文提出的算法中，邻域设置为大小为3 像素的正方形。在这种情况下，ujk包含在它的8 个相邻点的邻域中。当计算关于ujk的导数时，本文只保留包含ujk的部分，将式(12)改写为

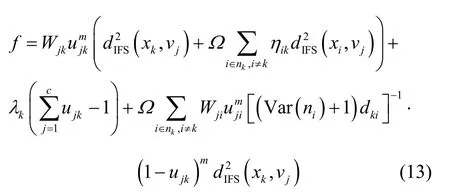
对零梯度条件的ujk求导并将模糊因子m设为2，令，同时令⋅，则有

实验所用参数及其含义如表1 所示。

表1 参数及其含义

4 分割性能测试及分析

为了验证本文算法的性能，采用Terravic 动态红外数据库（terravic motion IR database）与FCM、FLICM[22]、KIFCM[23]、GQFCM（set generator based on fuzzy c-means clustering algorithm）[24]、IFCM[25]和PIFCM（novel adaptive clustering algorithm based on a probabilistic similarity measure over atanassov intuitionistic fuzzy sets）这6 种广泛使用的分割方法进行对比。采用的数据集为本实验室利用FLIR E75热像仪获取的300 幅不同类型、不同背景的电力设备图像，包含的电力设备类型有绝缘子、设备线夹、隔离开关、穿墙套管等，同时在图像还存在复杂的背景，如人造建筑、植被、云雾天气和通勤车辆等。数据集中每幅图像的大小均为320 像素×240 像素。

假设实验中使用的红外图像包含电力设备和背景两部分，故本文算法的聚类数为2。对于FCM、FLICM、IFCM、GQFCM 等其他基于聚类的算法，通过一系列测试，将聚类数设为3，将灰度值强度最高的聚类设为电力设备类，IFCM 算法和PIFCM算法中生成函数的指标设为0.9 时取得了较好的效果。特别地，本文对KIFCM 算法采用与文献[26]相同的参数设置。

本文先对Terravic 动态红外数据库进行测试。选择该数据集中“户外运动场景”（场景1：2 个受试者分别从对面方向进入视场。他们先朝对方走来，穿过小路，一直离开，共计649 张图）、“户外运动场景”（场景2：一位受试者走在与摄像机感应器垂直的一条直线上。受试者先背对镜头向前走，然后转过身回到镜头前，共计1 300 张图）与“室内走廊监控场景”（场景3：监控室内走廊。在走廊的尽头有一扇门，受试者在那里离开并进入大楼，共计8 785 张图）等3 种不同场景进行图像分割检测，分别通过FCM、IFCM、本文算法3 种分割算法对上述3 种场景进行分割，结果如图5 所示。

图5 3 种算法对不同场景的分割结果

通过图5 可以看出，由于FCM 算法基于单像素的灰度值强度，使用的是距离不超过二维数据的欧几里得距离计算方法，导致其不能区分高强度的非目标对象并无法分离灰度值强度不均匀的目标信息；IFCM 算法基于单像素灰度值强度、局部均值和标准差，加入高斯核函数适合分割图像，较FCM 算法而言具有更好的灰度值强度不均匀问题。相对FCM 算法与IFCM 算法，本文算法可以有效地分离出目标信息，并对目标信息轮廓有着较精准、多层次的分割效果。为了验证本文算法相对于另外2 种经典分割算法的有效性，利用错误分类误差（ME,misclassification error）对上述3 种方法在不同场景的下的分割精度进行对比，如图6 所示。

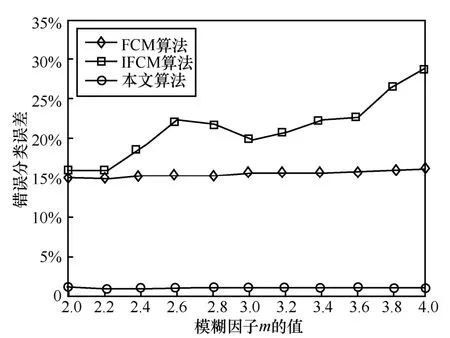
图6 3 种分割算法在不同m 值下的错误分类误差值

ME 是计算图像背景与图像目标错误分类的比率，反映图像目标与背景的误分类率，计算式如式(16)所示。

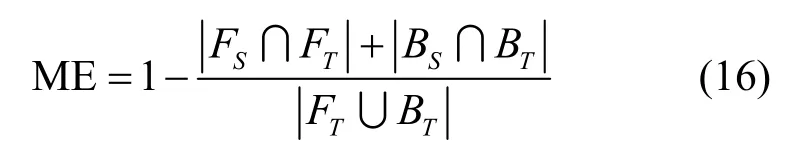
其中，FS和BS分别表示前景区域和分割结果的背景区域，FT和BT表示真实目标的相应区域，运算符∩表示测量重叠区域，∪表示计算图像总面积。ME 值越低，则意味着分割结果的质量越高。

所测试的300 幅电力设备红外图像数据集中包含几种典型的场景，分别涉及电力设备红外分割中的3 种主要问题，包括低对比度场景、高强度非目标物体介入和非均匀强度目标。

在低对比度场景情况下，电力设备会部分融入背景中，如图7(a)所示。电力设备轮廓的不明确性给精确分割带来了困难。特别是对于基于聚类的算法，不同聚类的中心位置非常接近，分割结果很容易呈现近乎全白或全黑的状态。

电力设备红外图像中通常会存在其他高强度目标，如图7(b)所示。虽然这些目标通常位于边缘区域，与真实目标相比具有不同的形状或结构信息，但是很多分割方法都很难忽略它们的干扰，而这主要是由于强度信息是这些方法的主导因素。

由于散热量的物理性质不同，电力设备在热成像中不可避免地呈现出强度分布不均匀的状态。这一特征往往会导致分割结果破碎，严重影响分割质量，如图7(c)所示。

图7 3 种典型场景

图8 给出了一些典型场景的分割结果，这些场景含有大量人造建筑背景的红外图像，具有明显的低对比度特征，这是分割的难点。如图8 所示，穿墙套管的轮廓几乎与背景混在一起。对于FCM、FLICM、IFCM、KIFCM 等基于聚类的算法，由于现有的空间信息不足，导致聚类中心的值都非常接近，分割后图像的背景依然存在。GQFCM 算法只能分割位于相对清晰边界上的穿墙套管的一小部分。而PIFCM 算法和本文算法得到了接近真实的结果。但是，如果将PIFCM 算法与本文算法的结果和真实图像进行比较，可以发现目标的边缘部分在PIFCM 算法的结果中有不同程度的丢失。与其他算法相比，本文算法抑制了噪声和杂波的干扰，在低对比度情况下保留了更多的边缘细节。

图8 各种算法对低对比度典型场景的分割结果

图9 各种算法对含高强度非目标物体的典型场景的分割结果

图9 为包含高强度、表面反射的非电力设备的场景。FCM 算法和KIFCM 算法由于没有包含空间信息，其结果受表面反射的影响较大。IFCM 算法、PIFCM 算法和FLICM 算法的计算结果均包含了较完整的设备整体。然而，它们不能完全区分设备与非设备。GQFCM 算法和本文算法可以有效地消除非电力设备和反射的干扰，都得到了一个总体轮廓更接近实际的结果。但是GQFCM 算法的结果仍然包含了图像的一小部分非设备。一般来说，该算法在低对比度情况下性能稳定，能较好地处理高强度非目标物体。同时发现，该算法可以有效地改善非均匀性和反射问题。

图10 各种算法对含不均匀强度目标的典型场景的分割结果

如图10 所示，电力设备主体存在明显的强度不均匀性。由于缺乏局部空间信息，几种基于模糊聚类的算法得到的结果都不理想。FLICM 算法的结果更加完整，但是丢失了绝缘子的一部分，这可能会对后续的处理操作产生重要的影响。结果表明，该算法在保留目标细节的同时，有效地抑制了目标的不均匀性。

为了验证本文算法的有效性，通过相对前景区域误差（RAE,relative foreground area error)[27]来综合判断各种分割算法分割结果的质量。RAE 反映了目标分割的精准度，在对电力设备图像分析的应用中，主要关注的是前景而不是整个图像，因此对电力设备是敏感的。RAE 的表达式为

由式(17)可知，在实际应用中，RAE 值越低，分割效果越好。各种分割算法的RAE 如图11 所示。从图11 中可以看出，本文算法相对于其他算法而言，在模糊因子m的范围内保持相对稳定的相对区域误差值在10%左右，并得到了最优RAE 值。结果表明，本文算法对模糊因子m的变化具有较强的稳健性和有效性。

图11 不同m 值下被测模糊聚类算法的相对区域错误率

由于本文算法是在IFCM 算法的基础之上引入了局部信息，相比于传统IFCM 算法增加了计算复杂度，因此本文算法计算效率有所降低。为了验证这种牺牲是否在可接受范围内，本文在普通PC 机上对不同算法的计算时长进行了测试。如表2 所示，测试的图像大小均为320 像素×240 像素。从表2 中可以看出，正常一幅图像处理时间仅仅增加了3 s，在实际应用中很难察觉，而且，也可以通过并行处理，或者更换更高性能计算机方式解决时间问题。而本文处理效果却很难通过其他手段改善。

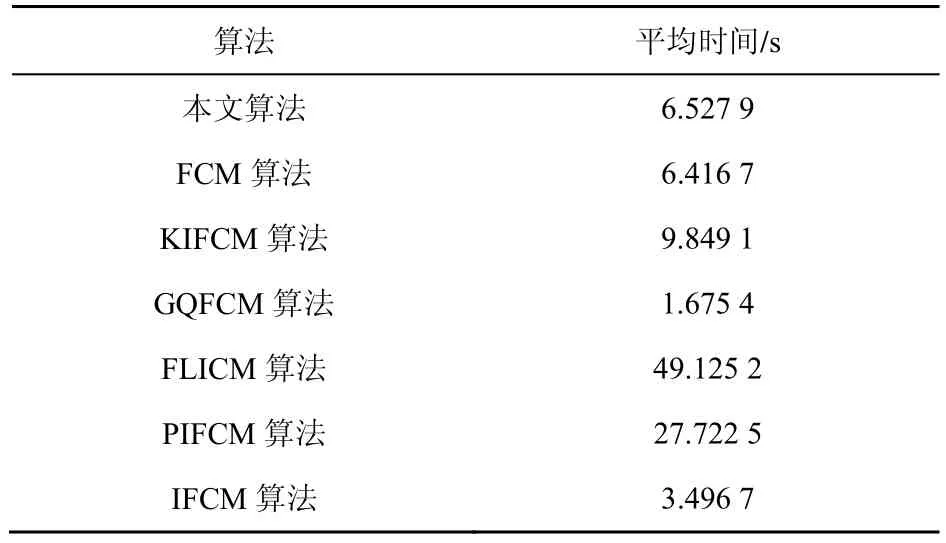
表2 各算法执行所用平均时间

5 结束语

随着无人机遥感领域的快速发展，红外无人机对电力设备高效的巡查效率与实时监测作用使其受到了越来越多的关注与研究。红外无人机拍摄获取电力设备数据后，对电力设备热故障的诊断将是一个重要的研究方向。本文就该问题提出了一种引入空间分布信息的电力设备红外图像分割IFCM 算法。由于存在电力设备与背景之间的低对比度，并且高强度的人工建筑、通勤车辆和云雾等非电力设备的干扰，其通常对设备分割带来严重影响。同时，表面不均匀散热也会导致红外图像的灰度值分布不均匀，使分割后缺失部分目标轮廓。针对以上问题，设计了一种引入高斯模型的全局空间分布信息的模糊聚类算法。该算法采用新的测距方法，使各像素的隶属度随距离的变化而改变，有效地抑制高强度背景，在分割结果中突出有效目标。在此基础上，结合局部方差和邻域隶属度组成的直觉模糊c均值组成的局部强度分布信息。利用直觉模糊距离和局部分布信息来解决强度不均匀的问题。在包含300 幅图像的电力设备数据集上测试了本文算法与其他类似算法的分割效果。在通过对结果的视觉效果和定量比较后得出结论，本文算法在对相同电力设备图像分割后的有效目标细节保留及精准性方面优于其他聚类算法，为解决目前电力设备红外图像分割的研究方向提供了一个新选择。