中美高中数学教材“圆锥曲线”内容比较研究
2020-06-05朱树金
朱树金
【摘 要】 对中美高中数学教材中“圆锥曲线”内容从内容呈现特征、内容呈现结构、例题与习题四方面进行比较研究.内容呈现特征方面,中国教材信息技术使用数量少但方式均衡,注重数学史的融入,美国教材色彩艷丽,形象直观,信息技术运用数量多但主要应用于解题;内容呈现结构方面,中国教材具有连续性好、系统性强的优点,美国教材知识完整性好,两国教材概念引入方式、知识点的广度略有差别;例题方面,两国教材的例题数量和类型无较大差别,且都注重数学图和旁白的插入,但美国教材例题表现形式更加丰富,求解过程更加详细;习题方面,美国教材习题比中国教材数量大、类型多,且重视重复性的练习,重视探究开放题.并据此提出了我国教材编写的思考与建议.
【关键词】 圆锥曲线;中美;教材比较
1 问题提出
教材是根据课程标准编写的教学规范用书,是老师上课的主要参考材料.英国剑桥大学Ken Ruthven在2014年数学教材研究与发展国际会议中指出:当今数学教材的形式及其在数学教学中的地位发生了很大变化,对教材的研究分析应该受到人们更多的重视[1].
作为代数与几何交界处的内容,一方面,“圆锥曲线”是高中数学中十分重要的内容,同时也是高考中占比大、难度高的部分,蕴含着数形结合、函数与方程、转化与化归等丰富的数学思想;另一方面,“圆锥曲线”与科研、生产以及人类的生活具有十分密切的联系[2].然而,通过文献分析发现很多研究是从宏观层面分析一本教材或者几何与代数等的某一模块内容,很少有研究者去研究一个特定数学内容概念化、结构化的呈现方式[3],而关于“圆锥曲线”部分的研究就更少之又少了.通过对中美教材“圆锥曲线”部分进行比较研究,改进课程与教学,可以帮助学生掌握数学的思想方法,提高学生的学习成绩,使学生认识到圆锥曲线与其他科学的联系并将其应用到实际生活.
本研究选取中国和美国数学教材“圆锥曲线”内容作为研究对象,从内容呈现特征、内容呈现结构、例题与习题四方面进行比较,分析两个国家数学教材的特色与差异,总结教材中关于圆锥曲线部分的设计与编排启示.
2 研究设计
2.1 研究样本
国内选取使用范围最广的人民教育出版社2008年出版的数学A版教材《数学必修2》和《数学选修2-1》(以下简称人教版);美国没有全国性的教材评审机构,联邦政府教育部没有对中小学教材进行审定的责任与义务,教材的评估与选定根据各州的实际情况而定,因此选取美国使用范围很广的全球知名出版公司Pearson教育集团2008年出版的《Algebra2》(以下简称PR版)
.2.2 研究方法
定性描述与定量刻画相结合的方法.
3 研究结果
3.1 内容呈现特征
3.1.1 宏观比较
内容呈现结构的宏观方面将从内容所占页数、直观特点和栏目设置三个方面进行比较分析.
人教版“圆锥曲线”内容所占页数多于PR版,分别为为77页和59页,且两个版本教材每页所承载的内容量大体相同.
直观特点方面,PR版教材比人教版更加色彩艳丽、形象直观.PR版教材视觉效果华丽,将概念、定理等用不同色彩的底色衬托或者用方框标出,实物图、彩色照片的数量丰富,内容更加直观形象;人教版教材概念、定理等的标注没有PR版醒目直观,彩色图片等偏少.PR版教材视觉感受更加舒适,更加具有趣味性和感知性,但是图片繁多有可能分散学生对具体数学知识的注意力,对于抽象思维能力较高的高中生是否还要进行这样的处理需要教育学、心理学等相关研究者进行更加深入的分析研究.
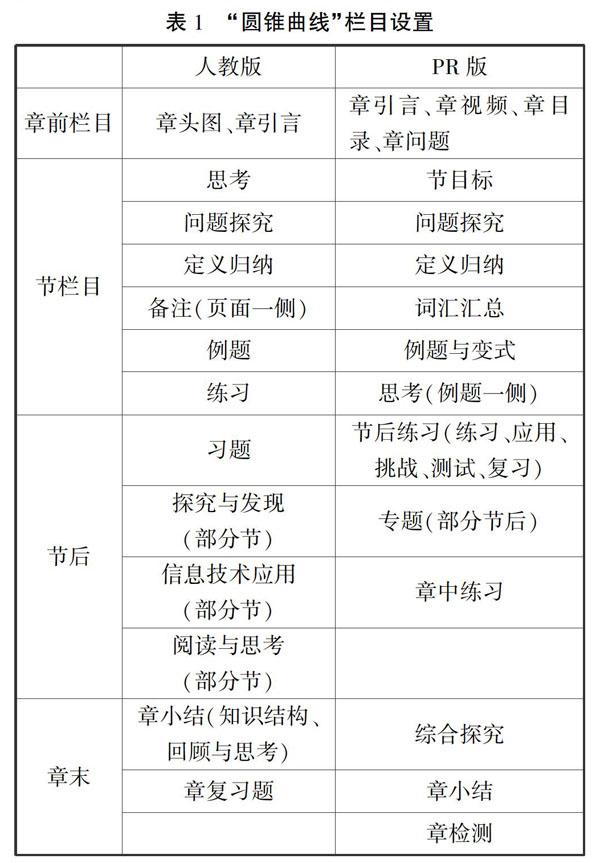
人教版和PR版“圆锥曲线”内容的栏目设置如表1.
人教版和PR版“圆锥曲线”内容栏目设置都十分丰富,各有特色.人教版阅读思考等为其特色栏目,提供一些数学史故事、数学问题供学生阅读;PR版节目标、专题为其特色栏目.
PR版教材可读性更强,有利于学生自学.PR版教材在一节内容开始之前列出该节学习目标,学生通过学习目标获得本节主要学习内容、重点内容等,从而更好地进行接下来的学习.当前高中生的抽象能力已经随年龄增长大大增强,及时引导学生进行自学有利于学生在不断解决数学问题、克服数学苦难的过程中逐渐增强学习信心,提高学生学习数学的兴趣,有利于教师有针对性地进行教学,增强学习效率[4].
PR版教材部分章节后面会有节后专题,主要介绍一种与前节知识相关的数学思想方法或技能,如在第一节“圆锥曲线探索”之后有“用图形计算器画圆锥曲线”的专题.这样的设计安排一方面可以帮助学生巩固所学知识,另一方面,学生使用计算软件的能力在专题训练中得到加强.
3.1.2 微观比较
内容呈现特征的微观方面从信息技术运用和数学史融入两个方面进行比较.
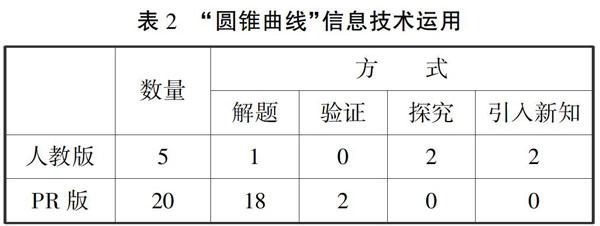
根据两版本教材信息技术使用的特点将信息技术使用方式分为解题、验证、探究、引入新知四类.解题为要求使用信息技术进行解题;验证为使用信息技术验证所得答案的正确性;探究为使用信息技术进行探究性的活动;引入新知为使用信息技术分析问题从而引入新的知识.人教版和PR版“圆锥曲线”内容信息技术使用的数量及方式如表2.
首先,PR版“圆锥曲线”内容信息技术运用数量远大于人教版;其次,人教版信息技术被均匀用于解题、探究和引入新知,而PR版主要用于解题;另外,人教版注重几何画板的使用,PR版注重图形计算器的使用;特别的,PR版会有信息技术的专题,如在第一节后的专题“用图形计算器画圆锥曲线图象”培养学生使用图形计算器的能力.
汪晓勤按照数学史与数学知识的关联程度,将数学教材运用数学史的方式分为五类:点缀式、附加式、复制式、顺应式、重构式[5].人教版“圆锥曲线”内容有两处数学史的融入,分别在章引言和阅读与思考部分,在章引言部分介绍了笛卡尔坐标系,在阅读与思考部分介绍了坐标法与机器证明的发展过程,融入数学史的方式均为附加式;PR版教材中无数学史的引用.3.2 内容呈现结构3.2.1 宏观比较
内容呈现结构的宏观方面将从内容所在章、前后章及本章各节安排三个方面进行比较分析.
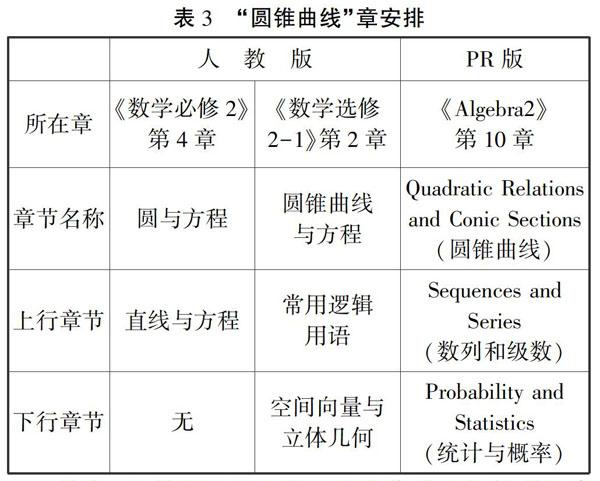
人教版和PR版“圆锥曲线”内容所在章、前后章如表3.
首先,人教版和PR版“圓锥曲线”内容所在章的设计安排存在不同.人教版圆锥曲线内容分布于《数学必修2》的第4章“圆与方程”和《数学选修2-1》的第2章“圆锥曲线与方程”,由于各地区学校的教学计划不同两本教材的学习时间也有所差异,一般分别在高一下学期和高二上学期进行学习;PR版教材圆锥曲线内容在《Alegbra2》的第10章“Quadratic Relations and Conic Sections(圆锥曲线)”.人教版“圆锥曲线”内容采用螺旋上升式的安排方式,分别在两本教材中完成圆锥曲线整个知识模块的学习,这样可以减轻学生的学习负担,但是明显增加了学生后续学习相关知识复习和回忆的压力,可能还造成部分学生因不能及时复习知识而增加学习新知的难度;PR版一次性学完“圆锥曲线”内容,短期内对学生形成相对完整的刺激,有利于整体知识模块的理解和记忆.
其次,人教版和PR版“圆锥曲线”内容与前后章节的联系也存在差异.人教版版在学习完“直线的方程”后学习“圆的方程”,在渗透了用代数解决几何问题的思想之后学习圆锥曲线;PR版圆锥曲线所在章上一章为“数列和级数”,下一章为“统计与概率”,与圆锥曲线均无直接关联,而“直线的方程”知识点安排在PR版的第2章“函数、方程和图象”中.人教版在进行知识模块的安排时更加注重知识间的联系,连续性更好,系统性更强,PR版更加注重知识的整体性,与前后知识模块的联系与人教版相比较弱.
人教版和PR版“圆锥曲线”内容各节安排如表4.
首先,人教版和PR版“圆锥曲线”内容主体部分相同但又各有特色.人教版“圆锥曲线”内容共包括7节,PR版共包括6节,两者主要包括圆、椭圆、双曲线、抛物线4节,人教版特有节为“直线、圆的位置关系”“空间直角坐标系”“曲线与方程”,PR版特有节为“圆锥曲线探索”和“圆锥曲线的变换”,其他节内容相对应.人教版更加注重图形间的位置关系,曲线与方程;PR版更加注重圆锥曲线的概念,圆锥曲线的图形变换.
其次,人教版“圆锥曲线”部分按圆、椭圆、双曲线、抛物线的顺序进行教材编写;而PR版按抛物线、圆、椭圆、双曲线的顺序进行教材编写.
另外,人教版“圆的方程”一章用到平面直角坐标系来解决与圆有关的一些平面几何问题,因此在此章的第三节学习空间直角坐标系,要求学生会用空间直角坐标系表示空间中的点,但无更多的应用,因此其位置设计安排有待人们进行更多的思考研究.3.1.2 微观比较
内容呈现结构的微观方面将从概念引入方式、知识点的广度、相同知识点的差异三个方面进行比较.
人教版和PR版“圆锥曲线”部分各概念的引入方式大体上“不谋而合”,且人教版引入方式相对更加丰富.两个版本教材都由平面截圆锥引入圆锥曲线的定义,都直接给出圆的定义;人教版先介绍了生活中的椭圆,然后通过用线和笔画椭圆引入椭圆的定义,PR版直接通过用线和笔画椭圆引入;人教版先类比椭圆然后通过用拉链和笔画双曲线引入双曲线的定义,PR版直接给出;人教版先举例再通过几何画板作图引入抛物线的定义,PR版给出抛物线图像后引入.
知识点指的是教材中单元标题、单元的下一级标题、教材中加粗或其他颜色标出的定义定理等.人教版和PR版“圆锥曲线”内容知识点如表5.
基于上述概念界定发现人教版版和PR版“圆锥曲线”部分知识点数量相差不大(38比36).由表可知两个教材的核心知识点基本相同,均由圆、椭圆、双曲线、抛物线的标准方程与性质构成,人教版另外给出了圆的一般方程、离心率等的概念,讨论了圆与直线的位置关系、圆与圆的位置关系;PR版另外注重圆锥曲线图像的移动,焦点不在坐标轴上的椭圆、双曲线、抛物线的一般方程.
中美两国高中数学教材中绝大多数知识点的表示方法都相同,但是由于基础教育阶段国际交流较少,所以中美两国高中数学中部分概念、性质、定理的表述和表达方式存在差异.如两个版本教材抛物线的标准方程定义不同,关于焦点在x轴正半轴上抛物线的标准方程人教版为y2=2px(焦点坐标为(p2,0)),PR版为 x=14cy2(焦点坐标为(c,0)).
3.3 例题
例题的宏观方面从数量和类型两个方面进行比较,例题的微观方面从例题的呈现形式和例题的求解特征两个方面进行比较.
按陈月兰等人[6]的例题分类方式,将例题分为纯数学例题和背景性例题,纯数学例题以数字、符号的方式呈现,不涉及任何现实问题情境,背景性例题以现实世界为背景;例题的表现形式包括数学图、非数学图、表、信息技术、旁白.人教版和PR版圆锥曲线内容例题的数量、类型和呈现形式如表6.
首先,人教版和PR版“圆锥曲线”内容例题数量和各类型占比无较大差别,例题数量人教版略大于PR版,分别为34和26,人教版纯数学例题的比例略高于PR版.
其次,人教版和PR版“圆锥曲线”内容例题的表现形式都十分丰富,都在例题中插入了大量的图片与旁白;PR版在例题中插入了更多的非数学图和表,这和PR版数学教材直观形象的特点相吻合;PR版在例题中同样注重使用信息技术解决或者验证数学问题,而人教版未涉及使用信息技术求解例题.
例题的求解特征方面,人教版通过简单分析后求解或者直接求解的方式求解例题,形式化、抽象化程度高;PR版会有更全面直观的分析过程,更详细的求解过程,这也和PR版更适合学生自学的特点相符合.
3.4 习题
3.4.1 宏观比较
习题宏观方面从习题的数量和类型进行比较.此处习题指教材中除例题以外的所有问题.人教版和PR版习题数量和类型如表7.
