基于逆可靠度法的三塔悬索桥主缆与中塔鞍座抗滑安全系数研究

边海滨

(中交一公局第五工程有限公司，北京市 100024)

1 引言

三塔悬索桥由于“中塔效应”的存在，中塔需要具备一定的抗推刚度来减小中塔的纵向位移和加劲梁的竖向挠度。若中塔抗推刚度过大，荷载作用下中塔两侧的主缆拉力可能相差较大，从而导致主缆与中塔鞍座滑移，进而影响整个结构的安全。因此主缆与中塔鞍座抗滑安全系数是三塔悬索桥设计的一个控制指标。

已经有学者针对主缆与中塔鞍座的抗滑性能开展了研究。张劲泉等以泰州大桥为工程背景，明确了多塔悬索桥的两个主要控制指标及对应的计算工况；郭济等计算了不同规范车辆荷载作用下某三塔悬索桥的主缆与中塔鞍座抗滑安全系数；姜洋等研究了不同桥塔的主缆滑动临界跨径，同时探讨了主缆与中塔鞍座抗滑安全系数的取值；王秀兰等基于活载作用下塔、缆变形和加载跨与非加载跨主缆内力的平衡关系给出了主缆与中塔鞍座抗滑安全系数的解析计算公式。上述研究成果均基于确定性模型进行主缆与中塔鞍座抗滑安全系数评估。周小燚和Xin等均基于随机车流从可靠度角度对主缆与中塔鞍座的抗滑性能进行了研究。

逆可靠度法用于求解目标可靠指标对应的未知设计参数。程进等基于逆可靠度法研究了悬索桥主缆的安全系数；Cheng等采用逆可靠度法评估了悬索桥的颤振安全系数；刘杰等将逆可靠度法用于评估连续梁桥悬臂施工整体抗倾覆稳定安全系数；蒋伟等采用逆可靠度法评估了钢管混凝土拱肋的稳定性；苏永华等将逆可靠度法和响应面法相结合用于评估边坡的稳定性；方砚兵等将逆可靠度法用于隧道支护抗力的计算。虽然逆可靠度法已经在多个工程领域得到了运用，但还未见在三塔悬索桥主缆与中塔鞍座抗滑安全系数评估中的应用。

该文在前人研究的基础上，以多塔悬索桥为研究对象，基于一次逆可靠度方法，提出一种主缆与中塔鞍座抗滑安全系数的计算方法。

2 逆可靠度方法

2.1 逆可靠度问题

逆可靠度法用于求解目标可靠指标对应的未知设计参数。文献[13]将逆可靠度问题定义为：

‖u‖-βt=0

(1)

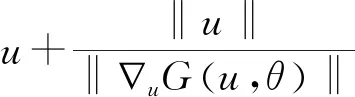
(2)

G(u,θ)=0

(3)

式中：βt为目标可靠指标；u为等价标准正态随机变量向量；uG(u,θ)为关于u的梯度算子；G(u,θ)为功能函数；θ为未知设计参数。

2.2 一次逆可靠度算法

文献[14]提出了一次逆可靠度算法，基本原理如下：

由FORM的基本原理可知：

(4)

假定未知参数θ的迭代初值为θ0，同时将极限状态方程在θ0处进行泰勒级数展开：

(5)

整理式(5)可得：

(6)

给定目标可靠指标βt、收敛误差ε、随机变量迭代初值u0和未知设计参数初值θ0，计算uG值，按照式(4)更新随机变量u1，计算出G(u0,θ0)和∂G(u0,θ)/∂θ，按式(6)更新未知设计参数θ1，计算式(7)所示的收敛条件，若满足则停止迭代，输出结果，否则以更新的u1和θ1继续迭代直至满足收敛条件。

(7)

式中：ε为收敛误差，通常可取0.000 1。

3 实例分析

3.1 可靠度模型

文献[15]给出了鞍槽内主缆抗滑安全系数K的计算表达式：

(8)

式中：μ为主缆与槽底或隔板间的摩擦系数；αs为主缆在鞍槽上的包角；Fct为主缆紧边拉力；Fcl为主缆松边拉力。

参考式(8)，采用式(9)作为功能函数：

(9)

文献[4]中给出了“单跨满布，跨中加力”时主缆与中塔鞍座抗滑安全系数的解析公式，具体的推导过程可参考文献[4]，该文不再赘述，直接引用最后的计算公式。由文献[4]可知：

αs=θcl+θct

(10)

θcl=arctan(Vcl/Hcl)

(11)

θct=arctan(Vct/Hct)

(12)

(13)

(14)

(15)

(16)

(17)

δL=δLp+δLQ

(18)

(19)

(20)

(21)

C=pL2

(22)

(23)

(24)

δfcl=δfcl,p+δfcl,Q

(25)

(26)

(27)

式中：θcl、θct分别为塔顶两侧主缆与水平线的夹角；Vcl、Vct分别为塔顶两侧主缆拉力的竖向分力；Hcl、Hct分别为塔顶两侧主缆拉力的水平分力；Kt为中塔纵向抗推刚度；Kc为主缆等效弹簧刚度；w为恒载集度；L为跨径；f为主缆垂度；p为均布荷载；Q为集中力；n为主缆垂跨比；Ec为主缆弹性模量；Ac为主缆截面积；δL、δfcl分别为荷载作用下塔顶位移和非加载跨主缆垂度改变量；δLp、δLQ分别为均布荷载和集中力作用下塔顶位移；δfcl,p、δfcl,Q分别为均布荷载和集中力作用下非加载跨主缆垂度改变量。

3.2 随机变量

以文献[4]中的算例为例(基本设计参数见表1)，采用逆可靠度法对主缆与中塔鞍座抗滑安全系数进行评估。

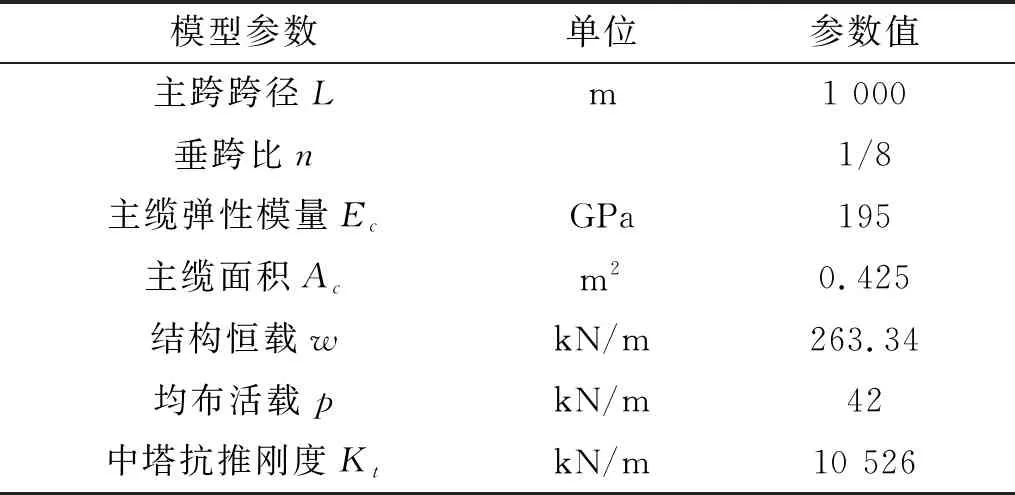
表1 基本设计参数

在算例进行主缆与中塔鞍座抗滑安全系数逆可靠度分析时，取随机变量为摩擦系数μ、w、p、Ec和Ac，各随机变量的统计参数取值见表2。

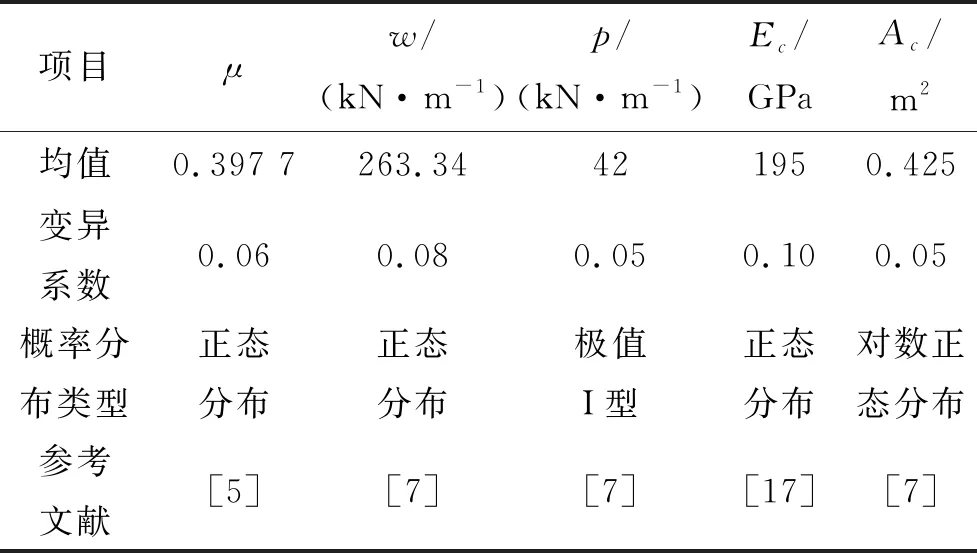
表2 随机变量分布类型及统计参数

3.3 抗滑安全系数求解

参照文献[18]，目标可靠指标βt分别取3.7、4.2、4.7和5.2，主缆与中塔鞍座抗滑安全系数K迭代初值取为2，不同目标可靠指标下主缆与中塔鞍座抗滑安全系数的计算结果见表3。

表3 可靠度水平对抗滑安全系数的影响

由表3可知：主缆与中塔鞍座抗滑安全系数随目标可靠指标的增大而减小，这是因为目标可靠指标越大，结构需要的安全储备越大，从而导致主缆与中塔鞍座抗滑安全系数减小。

不考虑参数随机性的确定性模型计算得到的主缆与中塔鞍座抗滑安全系数K为3.687 5，明显大于表3中的计算结果，说明不考虑参数随机性求得的主缆与中塔鞍座抗滑安全系数偏大，偏于不安全。因此在计算主缆与中塔鞍座抗滑安全系数时，有必要考虑参数的随机性。

3.4 参数分析

3.4.1 随机变量均值的影响

为探讨随机变量均值对主缆与中塔鞍座抗滑安全系数的影响，以目标可靠指标βt=3.7为例，控制各随机变量均值分别变化-15%～15%，而随机变量变异系数保持不变，求得的主缆与中塔鞍座抗滑安全系数与各随机变量均值的关系如图1所示。

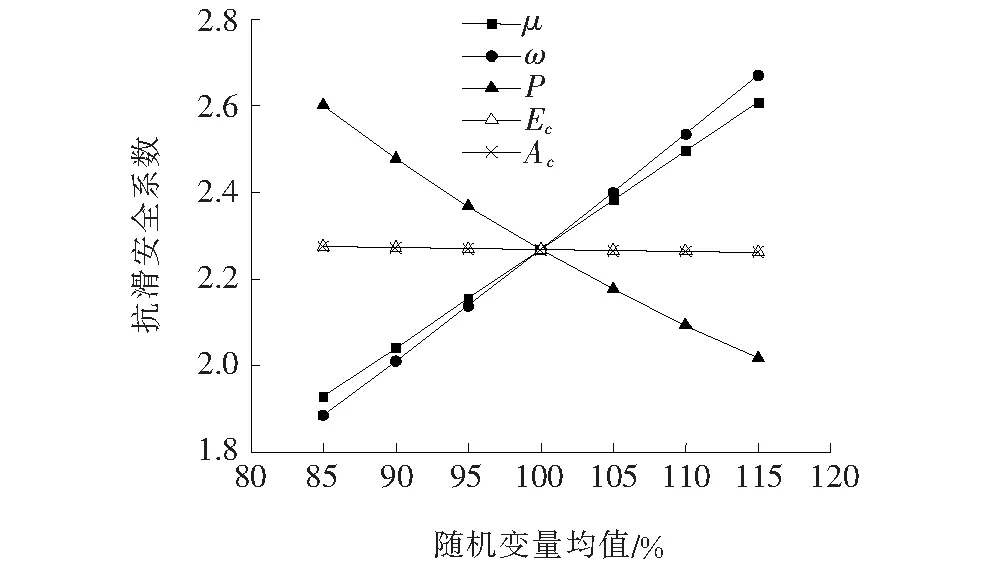
图1 随机变量均值与抗滑安全系数的关系

由图1可知：主缆与中塔鞍座抗滑安全系数对摩擦系数、结构恒载和均布活载敏感；主缆弹性模量和主缆面积对主缆与中塔鞍座抗滑安全系数的影响很小；主缆与中塔鞍座抗滑安全系数随着摩擦系数和结构恒载均值的增大而增大，说明可以通过增大摩擦系数和增加结构恒载来提高主缆与中塔鞍座抗滑安全系数；主缆与中塔鞍座抗滑安全系数随着均布活载均值的增大而减小，说明可以通过限制汽车荷载来确保主缆与鞍座不发生滑移，从而保证结构安全。

3.4.2 随机变量变异系数的影响

为探讨随机变量变异系数对主缆与中塔鞍座抗滑安全系数的影响，以目标可靠指标βt=3.7为例，控制各随机变量变异系数分别变化-15%～15%，而随机变量均值保持不变，求得的主缆与中塔鞍座抗滑安全系数与各随机变量变异系数的关系如图2所示。

图2 随机变量变异系数与抗滑安全系数的关系

由图2可知：主缆与中塔鞍座抗滑安全系数随着参数变异性的增大均呈现递减趋势；主缆与中塔鞍座抗滑安全系数对结构恒载的变异性最为敏感，其次是摩擦系数，对主缆弹性模量和主缆面积不敏感，因此在以后分析时可将主缆弹性模量和主缆面积作为确定性参数；在实际施工时应该严格控制结构恒载的变异性，确保施工质量与安全。

4 结论

(1) 基于逆可靠度法提出了三塔悬索桥主缆与鞍座抗滑安全系数的评估方法，求得的主缆与鞍座抗滑安全系数在满足目标可靠指标的同时考虑了结构中存在的参数变异性。

(2) 主缆与中塔鞍座抗滑安全系数随目标可靠指标的增大而减小，在分析时应合理确定目标可靠指标。

(3) 不考虑参数随机性求得的主缆与鞍座抗滑安全系数偏大，基于逆可靠度法求得的主缆与鞍座抗滑安全系数更为合理。

(4) 摩擦系数、结构恒载和均布活载对主缆与鞍座抗滑安全系数的影响较大，而主缆与鞍座抗滑安全系数对主缆弹性模量和主缆面积不敏感。