小子样下导电滑环磨损失效仿真的可靠性评估研究
2020-06-05孙远航余建波刘贤军孙习武王永松
孙远航,余建波,刘贤军,孙习武,王永松
(1. 同济大学机械与能源学院, 上海 201800; 2. 上海航天设备制造总厂, 上海 201100)
0 引 言
导电滑环作为卫星太阳电池阵驱动机构(SADA)的核心航天机电部件,其主要作用为在相对旋转的太阳帆板和星体间传输电功率与信号,是整星少数几个单点失效环节之一,其失效机理复杂,且要求其具有高可靠性、长寿命、高稳定性[1]。而导电滑环由于磨损常导致信号传输的不稳定甚至无法传输信号,使整个航天任务失败。导电滑环由其触头与汇流盘形成摩擦副,再通过摩擦副传递电流与信号,通过接触载荷保证触头与汇流盘稳定接触,传输过程中伴随有热量产生。导电滑环摩擦副在多场耦合影响下磨损加剧,随着磨损量的增加,滑环传输性能逐渐变差。
导电滑环性能试验过程复杂且耗时长,使得获得导电滑环的失效样本数据困难,以往基于大样本数据的评估方法不再适用。因此,建立导电滑环的磨损失效物理模型,是获得滑环磨损数据的有效方法,但物理模型获得数据往往具有小子样特点,进而难以进行大样本的可靠性分析。
目前可靠性分析领域中涉及机构部件的载流摩擦研究出现很多方法,其中吴杰等[2]采用试验方法对载流摩擦在不同载荷、速度、电流下的磨损研究,但需要进行大量试验且耗时长,且并未考虑机构的可靠性问题。任志玲等[3]基于弓网试验数据,应用量子遗传算法优化支持向量机的相关参数,建立受电弓滑板磨损率的预测模型,但试验数据获得周期较长,且该方法未考虑磨损过程的随机性问题。尹念等[4]应用分子动力学模拟滑环摩擦副的磨损过程,但是没有进一步研究滑环摩擦副的可靠性。刘强等[5-7]在基于机构磨损性能退化数据的基础上,结合随机阈值和小子样的可靠性分析法,得出机构的可靠性相关结论。阚琳洁等[8]提出性能退化和通用生成函数相结合的系统多状态可靠性分析方法,进行机构磨损的多性能参数退化下的系统可靠度分析。Ramalho等[9]应用磨损数据建立性能退化的可靠性评估,得出可靠性相关推论。Nicolai和Whitmore等[10-11]利用Wiener过程方法构建退化轨迹模型,进行可靠性评估。但是目前针对磨损的可靠性研究都是基于试验得到的大样本数据进行分析,或通过构建退化模型对结构可靠性评估,没有将两者有机结合分析机构可靠性。
综上所述,本文针对滑环失效特点构建多物理场耦合的导电滑环磨损失效模型,同时考虑导电滑环测量和装配随机误差,应用模型产生导电滑环小子样退化数据,结合小子样数据生成理论、随机失效阈值法,对导电滑环进行可靠性评估。
1 导电滑环磨损失效模型
1.1 问题描述
导电滑环由多个环道构成,盘式滑环结构如图1所示,通过滑环的各个触头与汇流盘各环道盘面接触形成摩擦副,将电流、信号等数据进行传输。导电滑环摩擦副在导电滑环运行过程中,由于电流传输、摩擦、接触载荷作用下,滑环摩擦副处在热力电多场耦合的环境,多场之间相互耦合加剧摩擦副磨损。其中,触头与汇流盘相对滑动,形成磨屑,随着磨屑量的增加,滑环信号传输产生短路、断路等现象,信号传输稳定性变差;当磨屑量累计到一定量时,导电滑环失效,因此磨屑量可作为表征滑环性能好坏的退化特征量,本文针对导电滑环摩擦副的性能退化特征量构建导电滑环的磨损失效模型,应用导电滑环的磨损失效模型来仿真导电滑环退化失效过程。
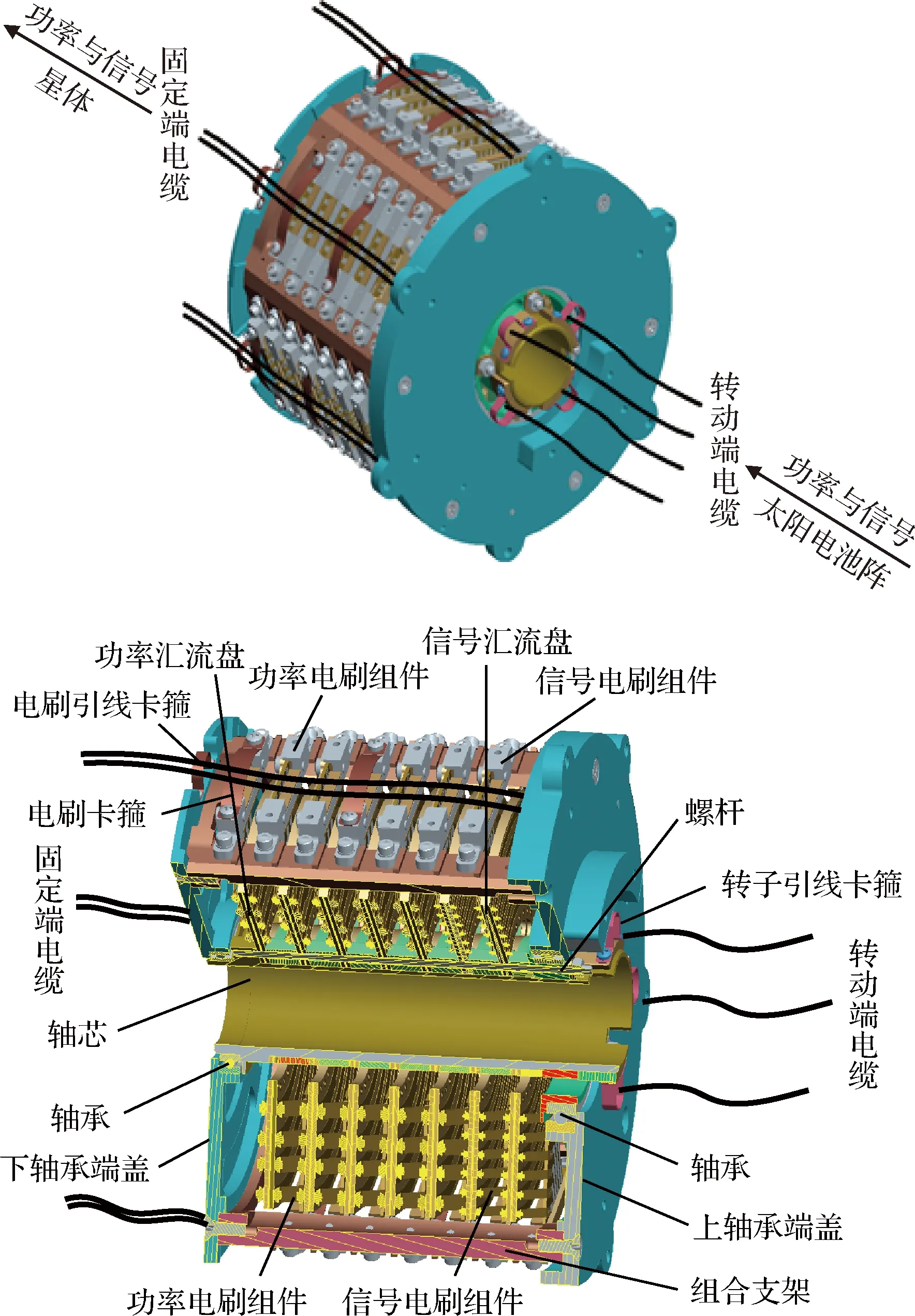
图1 盘式滑环结构图Fig.1 Disk slip ring structure diagram
1.2 导电滑环磨损失效模型
导电滑环摩擦副在磨损过程中,由于摩擦副热力电多物理场之间相互耦合影响,使滑环摩擦副的磨损程度难以计算。因此,本文结合赫兹理论、传热学、能量守恒、Archard模型解决滑环多物理场耦合对滑环磨损影响,建立导电滑环磨损失效模型。其中应用赫兹接触理论建立滑环摩擦副接触模型,预测接触载荷作用下触头的形状变化,计算在接触载荷作用下的摩擦副触头与盘面的接触面积,量化接触力对磨损影响;应用传热学建立摩擦副温升模型,计算摩擦副在运行过程中的温度变化,量化多场耦合对磨损的影响。基于Archard理论模型和本文构建的摩擦副接触模型、摩擦副温升模型构建滑环磨损失效模型,整个方案流程如图2所示。
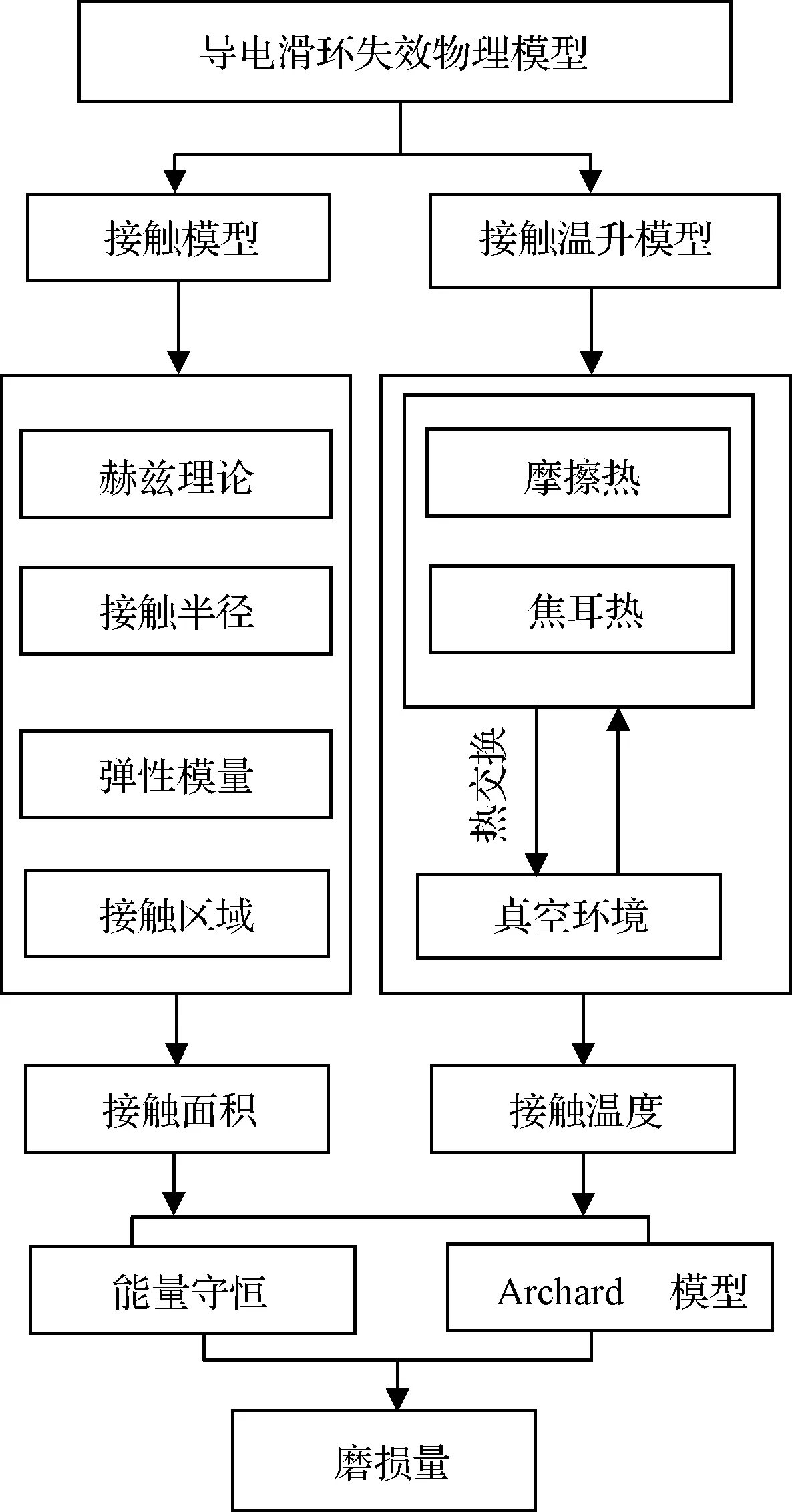
图2 导电滑环磨损失效模型构建流程Fig.2 The process of establishing the wear failure model of conductive slip ring
1.2.1导电滑环摩擦副接触模型
导电滑环触头与汇流盘在接触载荷作用下发生点接触,触头变形近似为椭球状;随着接触载荷增大,接触面积越大,接触面积直接影响滑环摩擦副的磨损。本文通过赫兹接触理论[12]计算摩擦副载流接触区域面积,摩擦副简化接触模型如图3所示。当触头与汇流盘接触,由于材料的弹性变形,使得接触点向邻近四周逐渐扩展成为近似圆形区域,根据赫兹理论可得接触区域的半径为:
(1)
式中:F为摩擦副之间的法向接触载荷,r和E分别为当量曲率半径和当量弹性模量,则摩擦副触头与汇流盘接触面积At为:
(2)
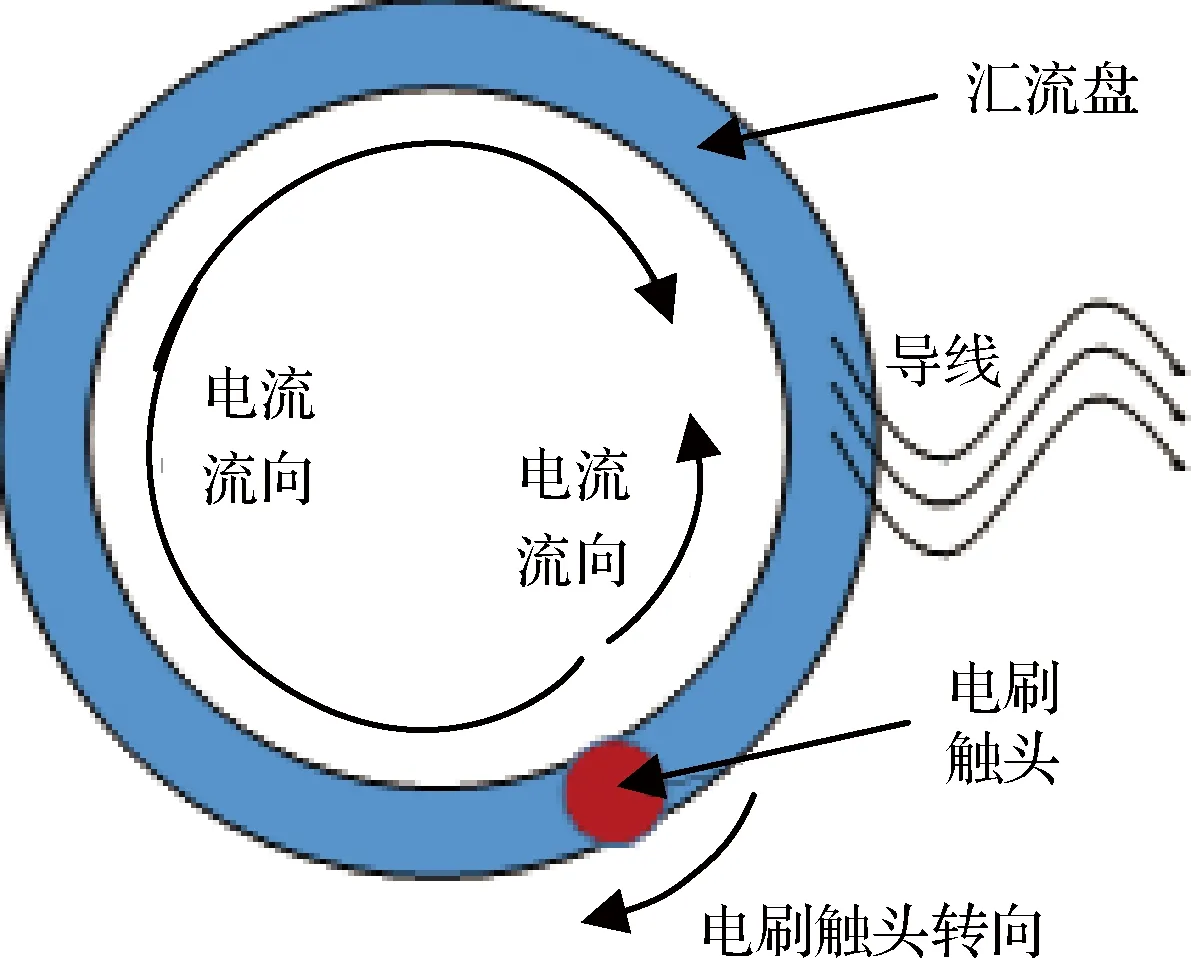
图3 导电滑环电流传输Fig.3 Conductive slip ring current transfer
1.2.2滑环摩擦副接触温升模型
导电滑环摩擦副在运行过程中,由于热力电多场耦合影响,产生热量,接触区域温度升高,同时由于接触区域温度高于周围环境,与周围环境进行热交换。导电滑环摩擦副热源主要是由电流传输、触头与汇流盘镀层摩擦产生,其中电流传输产生热量包括触头与汇流盘之间的接触电阻热、电流流经盘面产生的焦耳热。同时,导电滑环汇流盘面与周围环境进行热传递,因为导电滑环工作环境为真空,则热传递方式为热辐射。随着盘面温度升高,热辐射强度越大,当产热率与散热率相同时,导电滑环摩擦副温度趋于稳定,滑环摩擦副传热过程如图4所示。

图4 导电滑环摩擦副传热过程Fig.4 Heat transfer process of conductive slip ring friction pair
针对滑环摩擦副电流产热分析,电流传输产生的热量由两部分组成,一部分为触头与汇流盘之间的接触电阻和工作电流流经汇流盘产生的焦耳热,另一部分为触头与汇流盘摩擦产生的热量。针对接触电阻产热可直接进行计算:
P1=I2R
(3)
式中:R为触头与汇流盘之间接触电阻,I为导电滑环工作电流;而对于电流流经汇流盘产生的焦耳热而言,电流经过触头分两条之路流经汇流盘,最后经过导线传输到星体,滑环电流传输过程如图3所示,电流流经过程中,两支路的电阻值R1,R2随着触头运动处于动态变化,两支路并联之后电阻值为R3,则三者之间关系通过下式表示:
(4)
式中:R1与R2分别为电流流经盘面时的左侧与右侧盘道电阻值,两者随着触头位置变化而变化,R3为两者之间并联之后阻值;θ与r分别表示为触头对应转过角度和圆盘半径,ρ为盘面镀层材料电阻率。
当转速为nr/s时,则滑环摩擦副运转产生的焦耳热功率可表示为:
(5)
其中,摩擦热是由触头与汇流盘滑动摩擦产生,通过摩擦力做功方法直接计算:
P3=f·F·v
(6)
式中:v为滑环触头转速,f为触头与汇流盘之间摩擦系数。
导电滑环在真空环境下运行,其散热方式为通过热辐射方式传输热量,根据热辐射计算公式,可得滑环接触区域散热功率为:
(7)
式中:C0为黑体辐射系数,C0=5.76 W/(m2·K4),A为单个盘道面积,Tt为滑环摩擦副的温度值。
当散热功率与产热功率相等时,温度趋于稳定,用下式表示散热与产热功率相等时的关系:
P4=P1+P2+P3
(8a)
将式(3)、(5)-(7)代入式(8-a)可得:
(8b)
进而求得滑环运行稳态时温度Tt为:
(8c)
由接触稳态温度表达式(8c)可得知滑环摩擦副接触稳态温度由接触载荷、电流、滑环结构尺寸等决定。当电流、载荷、转速、电阻率、接触电阻增加时,滑环稳态温度升高,磨损加剧;当滑环盘道面积增加时,温度下降,符合滑环运行规律,证明了温升模型的合理性。稳态温度直接影响着滑环摩擦副的材料特性,进而量化热力电多场耦合对滑环摩擦副磨损的影响。
1.2.3基于Archard模型的滑环磨损失效模型
根据导电滑环目前研究可知导电滑环摩擦副磨损主要是黏着磨损,Archard模型[13]由于其所需参数少而广泛应用于机构摩擦副的磨损计算,本文应用Archard模型来计算摩擦副磨损产生的磨屑量,计算公式如下:
(9)
式中:S为摩擦副触头滑动路程,V0为磨损过程中产生磨屑量体积;kv为黏着磨损常系数,通过经验值给定[14];H为材料硬度,其受温度影响;F为摩擦副间的接触载荷。同时定义触头与汇流盘之间单位面积磨损程度表征量黏着磨损因子fm和表征滑环失效极限的摩擦副黏着磨损强度,σm,fm和σm表达式如下:
(10)
式中:At为滑环触头与汇流盘实际接触面积,已由1.2.1节部分求出。则滑环失效时运转的路程可表示为:
S=tmax·w·R=N·Tc·w·R
(11)
式中:tmax为滑环运行失效的时间,N为滑环失效时运转次数,Tc为滑环摩擦副运行一周的时间。摩擦副磨损过程中,触头与盘面结构在某一瞬间获得的能量密度分别为总能量的一半。令盘面结构镀层磨去厚度为δ1,触头结构磨去厚度为δ2,根据能量守恒可得到表达式:
(12)
由式(12)可得:
(13)
同时磨屑量体积和磨损接触面积满足下关系:
V0=δ·At
(14)
同时,当镀层厚度,材料硬度,磨损系数一定时,粘着磨损强度为定值。滑环受到材料、粘着磨损颗粒等因素的影响,所以实际粘着磨损强度表示为:
(15)
式中:n为安全系数,大于1;λm为材料影响系数。最后联立式(13)至(15)可得滑环摩擦副的失效方程:
F·C·kv·N
(16)
式中:C为滑环摩擦副周长,H1,H2分别代表触头、汇流盘硬度值。根据模型可以计算导电滑环摩擦副随着运转次数变化下的滑环摩擦副磨屑量,进而定量计算多物理场耦合对导电滑环磨损的影响。一般导电滑环的失效指标通常以磨屑质量作为失效阈值,则可通过式(16)计算的磨屑量体积与材料密度乘积作为参考。
2 滑环磨损可靠性评估方案
传统可靠性评估常将失效阈值作为固定值,忽略了同一型号部件由于制造误差、装配误差、周围环境差异等对部件性能的影响,因此工程实际中的失效阈值往往具有随机性。本文基于导电滑环磨损失效模型产生的仿真数据基础上对导电滑环的可靠性进行研究,流程如图5所示。具体流程如下:
1)考虑滑环制造、测量误差等随机因素对磨损的影响,对滑环磨损失效模型产生的仿真数据加入噪声,以贴近滑环磨损的真实工况。
2)针对滑环失效模型生成的数据量偏小特点,进行虚拟增广及Boot-strap扩展形成大样本磨损数据,用于导电滑环的可靠性评估。
3)应用数据拟合方法分别拟合扩展前后随运行次数变化的导电滑环磨屑量均值与标准差函数,基于导电滑环失效阈值的分布特性,分析扩展前、扩展后的固定阈值和随机阈值下的可靠性分布,得出更加贴近实际的可靠性结论。

图5 导电滑环失效阈值可靠性分析流程图Fig.5 The flow chart of reliability analysis failure threshold of conductive slip ring
3 导电滑环磨损退化数据扩展
3.1 导电滑环失效磨损仿真数据的获得
触头与汇流盘接触的好坏决定着信号传输的稳定性,滑环摩擦副的接触载荷使二者稳定接触,本文设置接触载荷为0.2 N,滑环的其他试验参数按照某厂制造的滑环工艺参数设定,具体参数如表1所示。
由于测量误差,实际接触载荷会在测量装置最小刻度上波动,实验测量装置最小刻度为0.02 N,则接触载荷测量误差在最小刻度范围内波动。因此基于装置测量误差,实际接触载荷在0.18~0.22 N范围波动,本文通过计算导电滑环失效物理模型在0.18 N,0.19 N,0.2 N,0.21 N,0.22 N,等5种载荷下的磨损来近似模拟滑环在接触载荷0.2 N下的磨损,考虑到滑环单圈的磨损变化量非常微弱,其额定寿命为60000 r,完全失效约在100000 r,所以本文以20000 r作为一个磨损周期,计算5个周期的磨损情况。同时由于导电滑环摩擦副镀层、触头的制造工艺的差异性以及工作环境等随机因素影响,在磨损数据加入高斯噪声近似模拟制造装配过程的随机误差,得到5组样本数据如表2所示。

表1 导电滑环组件性能指标Table 1 Performance index of conductive slip ring component
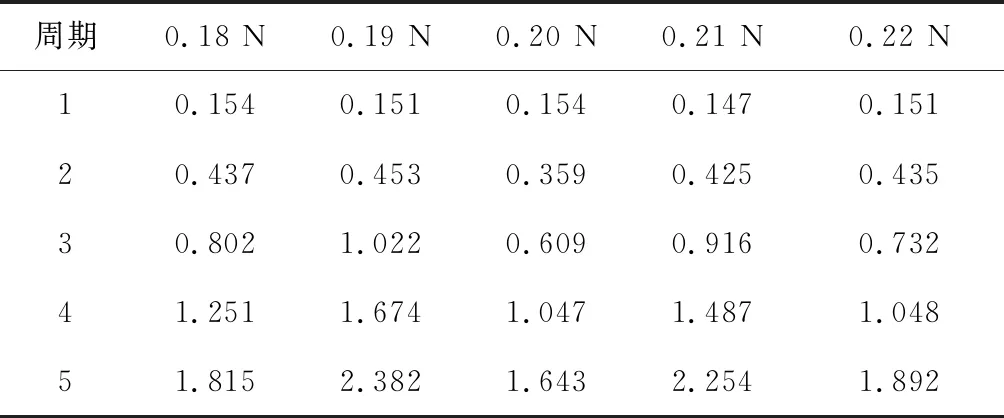
表2 不同接触载荷下各周期磨损量Table 2 Wear amount of each cycle under different contact loads g
3.2 磨损小子样数据扩展
根据导电滑环磨损失效模型得到了5组退化样本数据,但数据量偏少,无法更好的用于可靠性评估,因此采用虚拟增广法及Boot-strap法进行扩展得到大样本数据。首先,通过虚拟增广法[15]将表2中原始样本数目n=5增广到样本量n=13的样本数据,且每个样本数据容量仍为5,具体增广方法如下:

(17)
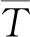
(18)
联立式(17)、(18)结合求解出ζ,进而求解出新样本数据,此时样本数据量扩展为13组,再采用指数Boot-strap法进行再二次扩展,利用样本本身的信息,对于总体分布不需要做出假设方法,结合虚拟增广数据及Boot-strap得到21组数据样本数据,如表3所示。

表3 指数Boot-strap扩展之后的导电滑环磨损数据样本Table 3 Slip ring wear data samples extended index Boot-strap
4 导电滑环失效阈值可靠性评估
4.1 滑环退化分布特征量
根据导电滑环磨损失效模型产生数据表2及经过磨损数据增广得到数据表3,进而计算导电滑环磨损量在各周期的均值和标准差,扩展前后的均值与标准差变如表4与表5所示。

表4 扩展前各周期的样本均值与样本标准差Table 4 Sample mean and sample standard deviation of each period before expansion

表5 扩展后各周期的样本均值与样本标准差Table 5 Sample mean and sample standard deviation of each period after expansion
根据表4与5数据可得扩展前后均值、标准差随运转周期变化的磨损量变化曲线如图6所示,由图6可以发现导电滑环扩展前后磨损样本数据的标准差、均值随着运转次数增加呈线性变化。本文应用最小二乘法拟合扩展前后样本数据均值和标准差随运转次数变化的函数为:
(19)
(20)
式中:t为导电滑环的运行次数,μ(t),σ(t)分别为磨损样本数据扩展后均值、标准差随运转次数变化的函数,μ0(t)与σ0(t)为磨损样本数据扩展前均值、标准差随运转次数的变化函数。

图6 扩展前后样本数据的均值标准差随运转次数变化曲线Fig.6 Variation and mean variance curve of wear sample data with operation times before and after expansion
磨损机构单位周期磨损量往往呈现正态分布规律[16],对导电滑环的磨损量仿真数据进行正态分布K-S检验,结果显示滑环磨损量在5种载荷磨损量下均服从正态分布规律,因此本文设定滑环在磨损过程的磨屑量呈现正态分布规律。
4.2 导电滑环固定阈值下的可靠性评估
传统的航天部件可靠评估分析中,常以失效阈值作为固定值。本文以某厂制造的导电滑环为例,其磨损经验失效阈值在1~1.2 g范围内波动,磨损量服从正态分布,固定阈值下的失效分布函数为:
(21)
进而可计算固定阈值可靠度函数R(t)为:
(22)
式中:t为导电滑环的运转次数,W为导电滑环运动过程中的磨损量,Wf为导电滑环磨损量的失效阈值,μW(t),σW(t)分别为磨损过程中均值、标准差随运转次数变化的函数,将式(19)、(20)代入式(22)可得滑环磨损数据扩展前后固定阈值下的滑环可靠度函数,分别计算固定阈值1 g、1.2 g下滑环可靠性分布函数,结果如图7所示。一般将可靠度等于90%时的寿命为产品的额定寿命,由图7中发现,扩展后的高可靠度阶段曲线比扩展前的曲线变化较平缓,较贴近生产实际;在可靠度较低阶段时,扩展后数据的可靠度变化曲线比扩展前数据变化快,也符合工程实际情况。
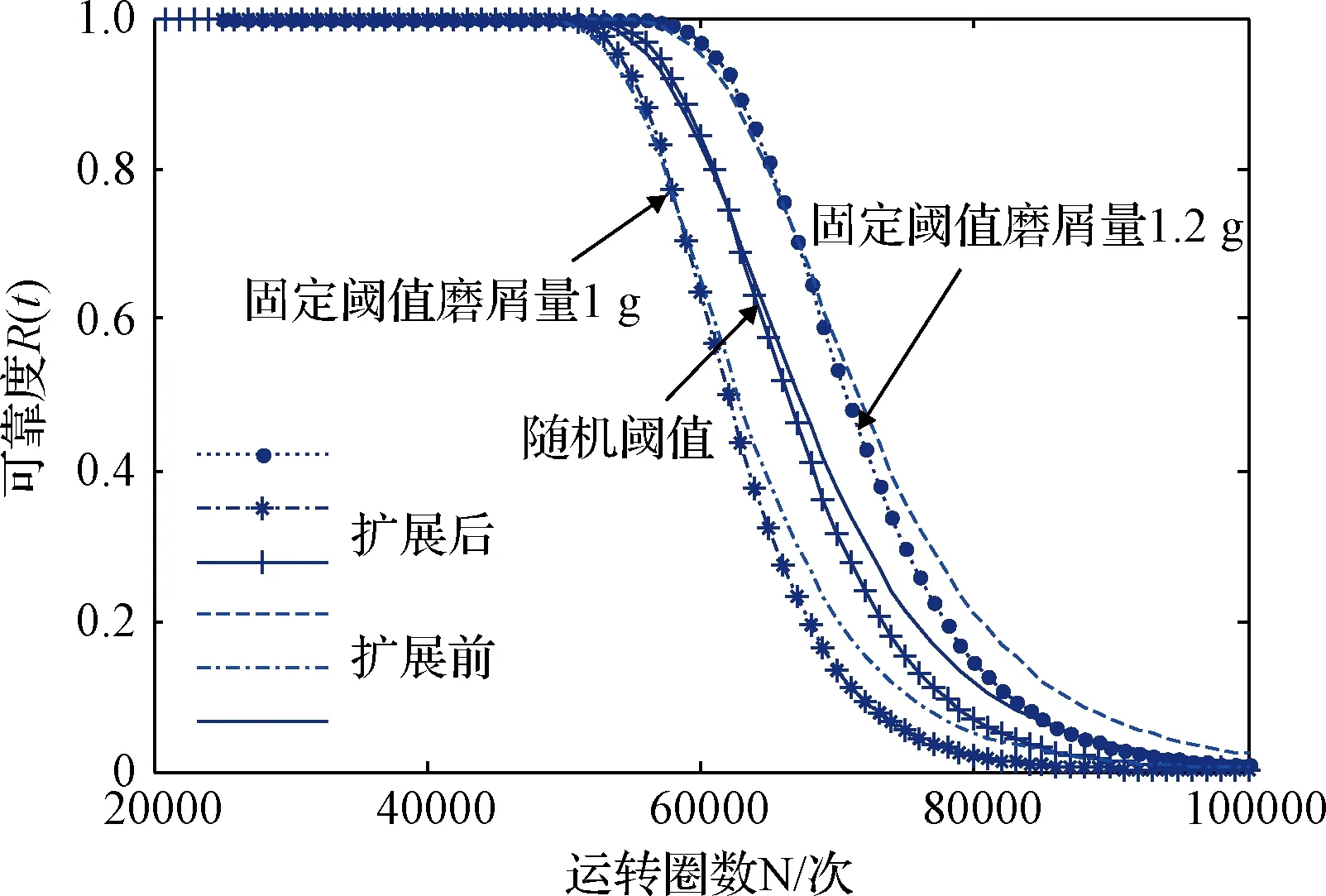
图7 导电滑环扩展前后磨损样本数据的可靠性分布Fig.7 Reliability distribution of wear sample data before and after expansion of conductive slip ring
4.3 导电滑环随机阈值下的可靠性评估
以往航天部件的失效可靠性评估分析,经常将阈值作为固定值进行分析,但是实际工程中由于环境、制造的差异原因,阈值并非为固定数值,因此将失效阈值设定为随机值更加符合工程实际,本文假设滑环失效阈值在1~1.2 g区间均匀分布且滑环磨损量服从正态分布,则滑环的失效概率密度函数和磨损量概率密度函数为:
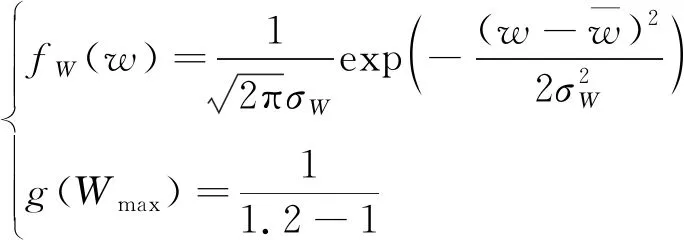
(23)

(24)
式中:R(t)与F(t)分别为滑环的可靠度函数和失效分布函数,μW(t)与σW(t)分别为滑环磨损量均值与标准差随运转次数变化的函数。将扩展前后均值、标准差函数代入可靠性函数中,得到随机可靠性曲线如图7所示。从图7中可以看出扩展后随机阈值在可靠度90%以上的持续时间高于扩展前数据可靠度,且在高可靠度阶段曲线变化平缓;在低可靠度阶段,曲线变化快,与实际工况更符合。证明本文提出的扩展数据方法具有合理性和可靠性。因此本文以扩展后数据对导电滑环进行可靠性评估分析,得到导电滑环可靠度函数如图8所示。

图8 基于扩展后数据在不同阈值下的滑环可靠性分布Fig.8 Reliability distribution of slip ring based on different thresholds of extended data
从图8中可以得到导电滑环部件不同阈值下的额定寿命分别为:53000次、58000次、63000次,本次试验的随机阈值额定寿命更加贴近实际,且在可靠度在90%之后变化幅度相比固定阈值平缓,随机阈值避免了以固定阈值作为失效极限造成的主观误差,更加贴近导电滑环的实际磨损情况。
5 结 论
1) 由于导电滑环真实磨损试验成本高、周期长的特点,建立基于多场耦合的滑环磨损失效模型。针对滑环摩擦副在多物理场耦合的特点,应用赫兹接触理论、传热学、能量守恒量化热力电多场耦合对磨损影响,结合Archard模型构建滑环磨损模型。基于磨损模型对滑环磨损过程进行仿真,得到滑环磨损仿真数据,为机构系统性能退化和可靠性研究提供数据。
2) 结合小子样的虚拟增广法、Boot-strap法对滑环磨损仿真试验数据进行扩展,并基于退化量分布特点得到扩展前后磨损量均值和标准差随导电滑环运行次数变化的函数。
3) 用扩展前后的磨损数据对滑环机构可靠度进行评估,得到固定阈值、随机阈值下的可靠度曲线对比图。扩展前后数据的可靠性曲线相似,且扩展后数据变化更加符合生产实际,证明数据增广方法的可靠性。同时为避免固定阈值可靠性评估分析的主观误差,应用随机阈值进行滑环的可靠性评估,结果表明基于随机失效阈值下滑环可靠性评估比固定阈值下可靠性评估预测的失效过程更符合生产实际。因此本文的方法填补导电滑环因缺少数据而难以进行可靠性研究的空白。
