土壤样品γ能谱分析中常用本底扣除方法探讨

（福建省辐射环境监督站福州分站，福建 福州 350005）

在对放射性核素进行能谱分析时，对能谱数据的处理大致分为两步，一是峰分析，即找出有意义的全能峰并计算出峰的净面积；二是根据峰的净面积计算出放射性核素的活度。对于土壤中的放射性核素分析，《土壤中放射性核素的γ能谱分析方法》（GB/T11743-2013）[1]中推荐了相对比较法、效率曲线法和逆矩阵法等三种能谱分析方法，但是对其中用到的全能峰净面积的计算方法没有提及。全能峰净面积是指放射性核素发射的某个特定能量的γ射线在谱仪中产生的有效计数，通过全能峰非面积扣减本底得到。全能峰非面积是指全能峰范围内的所有道址计数之和，可直接由测量获得。本底是由被测射线与探测器或周边介质发生各种相互作用而产生的干扰，以及测量环境中的天然辐射本底叠加而成，无法直接测量得到，只能根据一定算法估算出来。因此，本底估算的准确程度直接关系到全能峰净面积乃至放射性核素活度分析的准确性。

1 γ能谱本底组成分析

典型放射性核素的 γ能谱曲线如图 1（a）所示。能谱曲线的本底主要有 3个来源：①测量环境辐射本底，如图1（c）所示；②高能γ光子在探测器中的康普顿散射；③γ光子在探测器灵敏感区中的小角度散射。其中第 1类本底可以通过测量并扣除测量环境本底谱的方式进行扣减，因此本文中的本底扣减主要指第2、3类本底。康普顿散射产生出平缓变化的康普顿坪[2]，在峰区内可近似用直线来模拟。小角度散射则引入低能拖尾，使得光电峰出现左高右低的现象，如图 1（b）所示，它是峰净计数的积分函数。这两部分叠加起来，得到本文讨论的本底，其特征是一个随能量增加而平滑下降的函数[3]。其分布大致如图1（a）所示。

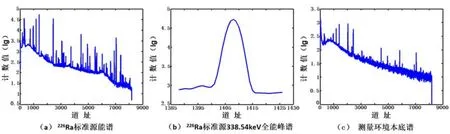
图1 典型能谱图

2 常用的本底扣除方法

本底抵扣方法包括峰区本底扣除法和全谱本底扣除法两种。峰区法是在包含全能峰在内的一个较窄的谱段内，对本底分布进行估计，再在峰区内逐道扣减掉本底数据。对于能量分辨率较高的HPGe谱仪，使用峰区本底扣除法即可得到较好的精度[5]。目前峰区本底扣除的方法主要有直线本底法、多项式最小二乘拟合法。全谱法需要估计出本底在整个测量能谱中的分布模式，然后再从谱数据中逐道减去本底在该道的计数。SNIP（Sensitive Nonlinear Iterative Peak ）法[3,5]是目前常用的全谱本底扣除方法。本文对上述三种方法进行分析。应用峰区本底扣除法时，需要先确定峰位及峰边界。本文采用基于核素库的峰位确定方法。确定峰边界时，由于高斯分布中 99.75%的有效计数出现在均值±3σ的范围内，σ约等于FWHM/2.35（FWHM为高斯峰的半高宽），峰区应在峰位两侧（-1.28×FWHM，1.28×FWHM）范围，但实际中的全能峰会有畸变致峰宽变宽，为尽量保留全能峰中的有效计数，在待测核素峰位两侧（-3×FWHM，3×FWHM）范围内，寻找出左右各1个最小计数值点作为全能峰左右边界。

2.1 直线本底法

直线本底法是用直线对峰区内本底分布进行拟合，再从谱数据逐道扣减拟合的本底数据，从而完成本底扣除。直线本底分布函数可描述为：

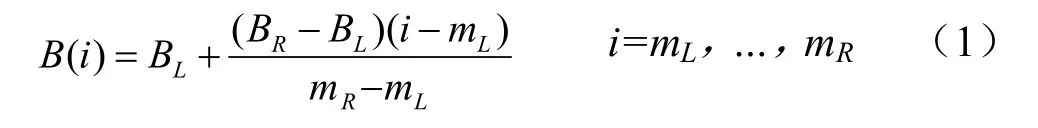
其中，mL、mR分别为全能峰左右边界道址，B(i)是道址i的本底值，BL是道址mL的计数值，BR是道址mR的计数值。为减小计数统计涨落对测量结果的影响，还可以使用峰边界附近若干数据点的平均值来进行线性拟合。

2.2 多项式最小二乘拟合法

当谱仪的能量分辨率较低，全能峰宽度较大时，如NaI谱仪，采用直线对峰区本底进行拟合将导致较大的误差[4]，直接影响本底扣除效果。此时多项式拟合更接近实际的本底分布，能取得更好的本底扣除效果。在全能峰边界非侧选取一系列平稳点作为本底点，并采用m次多项式对这些本底点进行最小二乘拟合，拟合曲线在峰区内的分布即为本底分布，可表示为：

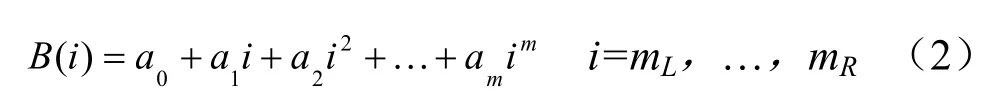
式中，a0，a1，…，am为多项式系数，可由最小二乘法确定。B(i)是道址i的本底值。多项式拟合时，为减小统计涨落带来的影响，也可以采用邻近几个数据点的平均值作为拟合的数据值。为保证多项式拟合的准确度，拟合时应注意：①拟合m次多项式曲线，需要有至少m+2个数据点；②应合理设置拟合次数，避免出现过拟合。

2.3 SNIP法

SNIP法通过简单的迭代算法来实现本底扣除。先通过LLS变换对全谱中每道计数进行变换，避免各道计数值的差异过大。LLS变换如下：

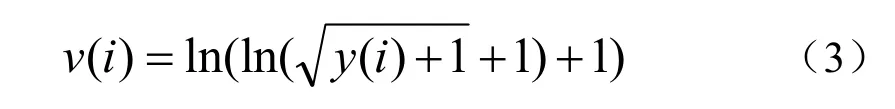
式中，y(i)为道址i的计数值，v(i)是变换后道址i的数值。然后对变换后的数据进行m次迭代计算，迭代公式为：

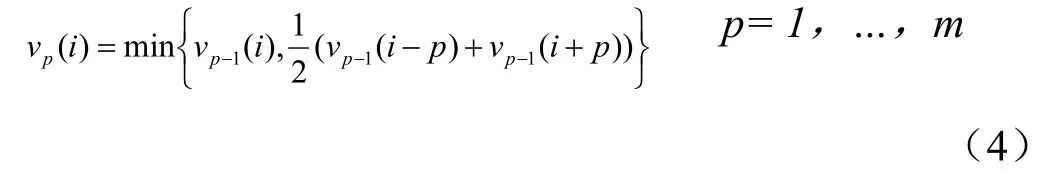
最后对迭代后的数据进行反LLS运算，即可得到全谱的本底分布。扣除全谱本底后，全能峰两侧净计数值应在0附近，由此确定全能峰边界道，得到全能峰区的SNIP本底分布。在SNIP法本底扣除时，迭代次数m的选择对于 SNIP算法的本底估计准确度有重要影响，相关研究发现，m值取在（w-1）/2附近（w为峰宽），可获得最好的全能峰本底扣除效果[3]。

3 几种本底扣除法比较

3.1 本底扣除方法的适用性分析

从式（1）可以看出，直线本底法由于只使用了峰区边界的计数，其准确度只与全能峰边界选取的准确性有关，而与峰区非侧的谱分布无关，适合于大多数情况下的本底扣除。同时由于真实本底并非均匀线性分布，在窄峰条件下，本底更近似线性，因此直线法在能量分辨率高、窄峰条件下会比宽峰条件下获取更好的效果。多项式最小二乘拟合法由于使用曲线来模拟本底分布，在可用于拟合的本底数据足够多的情况下，拟合出的平滑曲线更接近真实的本底分布，因此相对于直线本底法，其本底扣除精度更高，且峰区的宽度可以比较大。但当主峰非侧有突兀的干扰峰时，如果使用了干扰峰数据，拟合效果势必会产生较大偏差，如果干扰峰过大，导致拟合的本底曲线发生畸变、失真，甚至会引发本底扣除错误。因此，应用多项式最小二乘拟合法要求全能峰两侧有较宽的平缓谱段。如式（4）所示，SNIP算法的本底扣除效果与迭代次数密切相关，当合理选择迭代次数m时能有效抑制基底，且基本不会影响峰形和净面积。反之，迭代次数m选择过大或过小，会造成本底抑制不足或过量，影响本底扣除效果。

3.2 本底扣除效果比较

本文通过对标准体源进行 γ能谱测量获取实测数据，再使用Matlab软件对实测数据进行数据处理和分析。实验中采用的谱仪为ORTEC公司生产的P型宽能HPGe谱仪，型号为Dspec-Pro，非道数为16384道。用于测量的标准体源为中国计量院制作的40K源、226Ra源、232Th源和混合体标准源。由于HPGe谱仪具有较高的能量分辨率，实测中选用比较法作为能谱分析方法，对具有典型形态的全能峰采用不同本底扣除算法，计算放射性核素活度，通过比较活度计算误差，得到上述三种本底扣除算法的扣除效果优劣及适用性分析结论。几种典型全能峰包括：①无明显畸变高斯峰；②低能拖尾峰；③主峰区非存在干扰小峰。典型全能峰及其本底谱如图2所示，本底扣除效果如表1所示。

图2 典型全能峰及本底估计曲线

从表1可以看出，当全能峰无明显低能、高能拖尾，以及峰区非侧平坦无干扰时，上述三种本底估算方法本底扣除效果差别不大，三次多项式最小二乘法和SNIP法略优于直线本底法。当全能峰存在明显低能拖尾时，SNIP法本底扣除效果较好，显著优于直线本底法及三次多项式最小二乘法。当待分析全能峰非侧存在干扰峰时，3次多项式最小二乘法受干扰峰影响，本底曲线失真，如图 2（h）所示，本底扣除效果较差，而直线本底法和SNIP法基本不受干扰峰影响，本底扣除效果较好。因此，SNIP本底扣除法在各种峰型条件下都可以稳定获得很好的本底估计效果。从图2可以看出，由于合理选择了SNIP法的迭代次数，基本不影响全能峰的峰形和净面积。

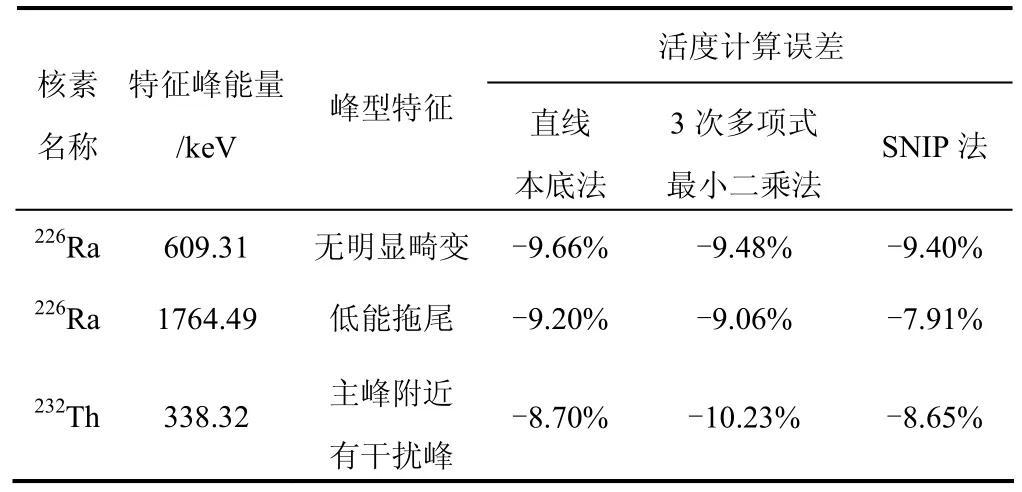
表1 典型全能峰本底扣除效果

3.3 结论

通过理论分析，以及实测数据验证，直线本底法在能谱分辨率高、峰区较窄的情况下，对各种峰型适应性较好，本底扣除效果稳定，且计算量小，实现过程简便，是目前普遍应用的一种本底扣除方法。SNIP法采用了迭代算法抑制基底的影响，能够稳定、准确地估算出本底，在前述三种方法中本底扣除效果最好，是较理想的一种本底扣除方法，缺点是计算量较大，实现过程复杂。多项式最小二乘法在全能峰非侧有较宽的平坦谱段时，可以得到较好的本底扣除结果，但当全能峰非侧有其他干扰峰时，就有可能造成本底曲线失真，使得本底扣除效果变差，因此应用多项式最小二乘法时应谨慎。

4 结束语

在对土壤中放射性核素进行能谱分析时，为了计算放射性核素净面积，需要对本底进行扣除。通过比较目前常用的峰区本底扣除法，发现在能量分辨率高、峰宽较窄的情况下，直线本底法、多项式最小二乘拟合法和SNIP等三种方法各有优势。应用中应根据全能峰峰型特征以及计算能力选取合适的本底估计方法，提高能谱分析的准确度。