基于分数阶微积分的岩石硬性结构面蠕变本构模型

李任杰, 吉 锋, 张津铭, 潘勇杰, 熊朝正

(成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059)

节理岩体普遍存在于岩体工程中,其力学性质等均较复杂,直接影响岩体的安全性。流变为岩石变形破坏中较为重要的一种表现形式,节理流变往往决定岩体的流变。岩体蠕变本构模型的研究是目前了解岩体蠕变特性的重点和热点[1]。目前应用较为广泛的本构模型构建方法主要为元件组合模型,其通过基本元件组合、改进以往的线性元件为非线性元件组合模型以及加入损伤参数等变量对蠕变过程进行拟合[2]。

孙海忠等[3]采用含分数阶导数的Kelvin模型对软土的黏弹性蠕变过程进行较好的模拟,并认为形式上简单统一,且参数少,具有较为广泛的应用前景。王红娟等[4]于Kelvin体黏性元件中引入分数阶函数,且弹性元件考虑弹性参数随时间变化,对黏塑性体进行改进,构建变参数非线性黏弹性蠕变模型,经过验证,模型模拟效果较好。陈家瑞等[5]通过引入分数阶Kelvin模型,解决了整数解Kelvin的拟合效果不好的问题,最终证明模型能够较好地模拟破碎泥岩的蠕变过程。郭佳奇等[6]将Kelvin模型中牛顿黏性体替换为含分数阶微积分的FC元件,最后通过元件组合模型,形成基于分数阶微积分的流变模型,通过与整数阶流变模型相比较,其模拟效果较好。黄海峰等[7]基于Riemann-Liouville理论,于黏性元件中引入分数阶微积分,使得更加符合岩石材料的流体性质,最终模型通过对红层泥岩及相关试验数据进行拟合,充分说明了本构模型的适用性。刘峻松等[8]基于分数阶微积分理论,对蠕变本构模型中的基本元件进行改进,最终构建一种新的三元件蠕变损伤本构模型,通过辨识砂岩的试验数据,证明了所建本构模型的合理适用性。唐皓等[2,9]利用分数阶微积分的软体元件替换西原模型中所有的黏壶元件,并将黏滞系数非定常化,得到分数阶微积分改进的黄土西原模型,对黄土蠕变试验数据进行辨识,结果证明模型的辨识效果较好。徐国文等[10]根据R-L分数阶微积分理论,提出分数阶微积分黏壶元件替换西原模型中的黏壶元件,结果表明模型能够较好地对蠕变三阶段进行反映。陈亮等[11]通过引入基于分数阶微积分的软体元件,对岩石蠕变的三阶段进行很好的模拟。

上述研究将分数阶微积分应用于蠕变本构模型中,且均取得较好的效果,但是多为完整岩石的蠕变本构模型,少有涉及贯通型硬性结构面和非贯通结构面的剪切蠕变本构模型研究。因此将分数阶微积分应用于非贯通硬性结构面岩体剪切蠕变本构模型中具有较为重要的意义。

针对非贯通硬性结构面蠕变试验及本构模型方面研究的缺乏,通过制作非贯通硬性结构面试样,进行剪切蠕变试验,揭示非贯通硬性结构面剪切蠕变特性,建立基于分数阶微积分的岩石硬性结构面蠕变本构模型。

1 剪切蠕变试验设计及成果

1.1 试验设计及试验设备

参考李银平等[12]所提利用云母片模拟结构面的方法,模拟硬性结构面,进一步制作非贯通硬性结构面的试验模型,进行剪切试验及剪切蠕变试验,揭示非贯通硬性结构面的剪切蠕变特性。试样制作采用类岩石材料及其比例为水∶水泥∶标准砂=3∶8∶8的比例进行水泥砂浆的浇筑,待其固结24 h后进行拆模,并于水中养护20 d后进行相关试验。试验所用试样制作流程如图1所示。

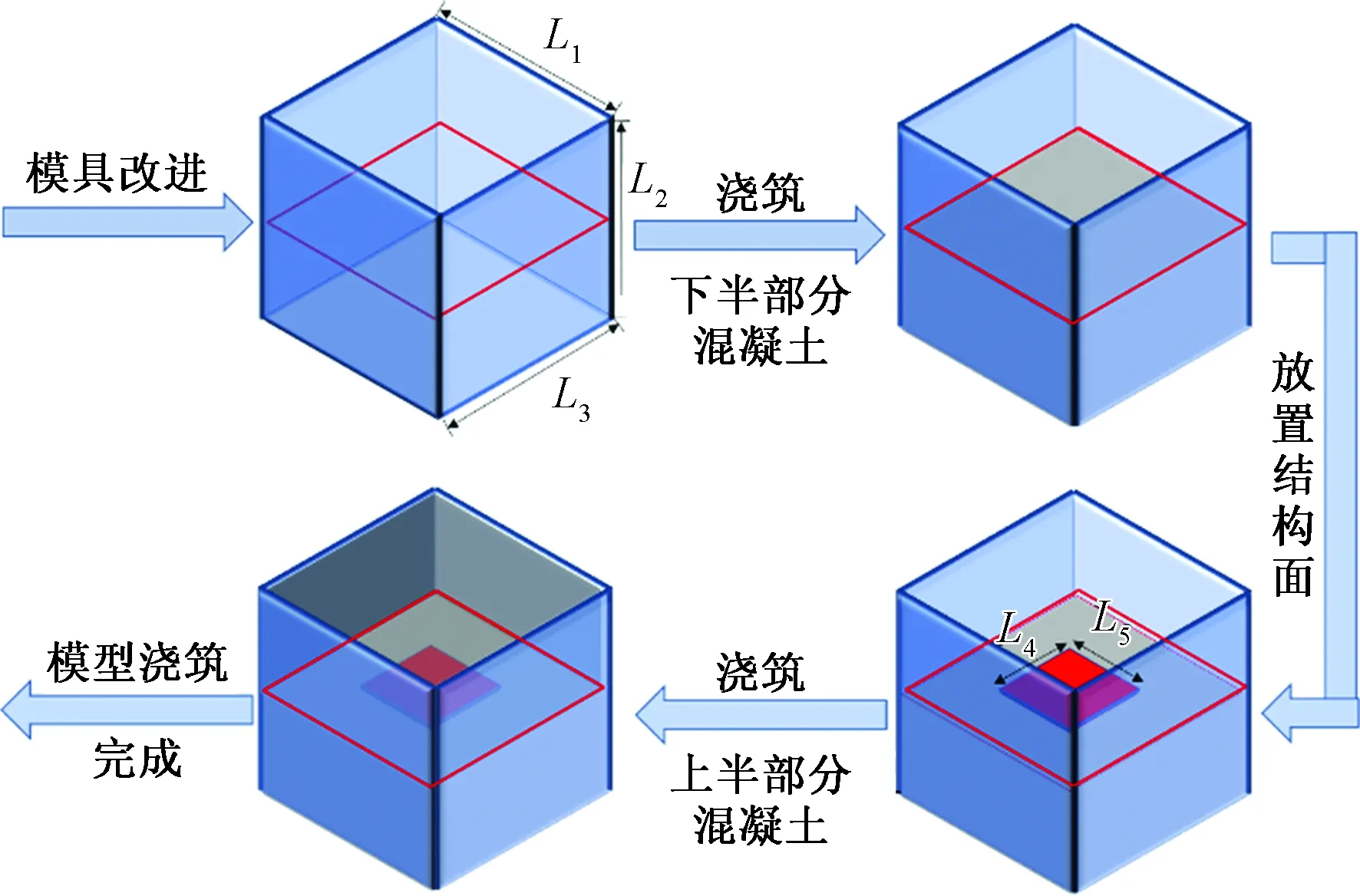
图1 模型制作流程Fig.1 Model making process

剪切蠕变试验在地质灾害防治与地质环境保护国家重点实验室自主研发的YZJL-300型岩石剪切流变仪上进行。

剪切蠕变试验基于单轴压缩试验和直剪试验的成果上,采用陈氏分级加载法,进行非贯通硬性结构面的剪切蠕变试验。对连通率k=(L4L5)/(L1L3)=0.64试样加载不变的正应力σ,由低到高加载剪应力τ,每级剪应力如表1所示,每级剪应力持续时间为48 h,直至试样破坏。

表1 剪切蠕变试验参数

1.2 试验成果

通过剪切蠕变试验,在应力加载瞬间或增大至下一级应力时,非贯通硬性结构面试样有明显的瞬时变形现象。同时,剪切蠕变试验过程中出现了较为完整的蠕变三阶段,即衰减蠕变阶段、稳速蠕变阶段、加速蠕变阶段,如图2所示。

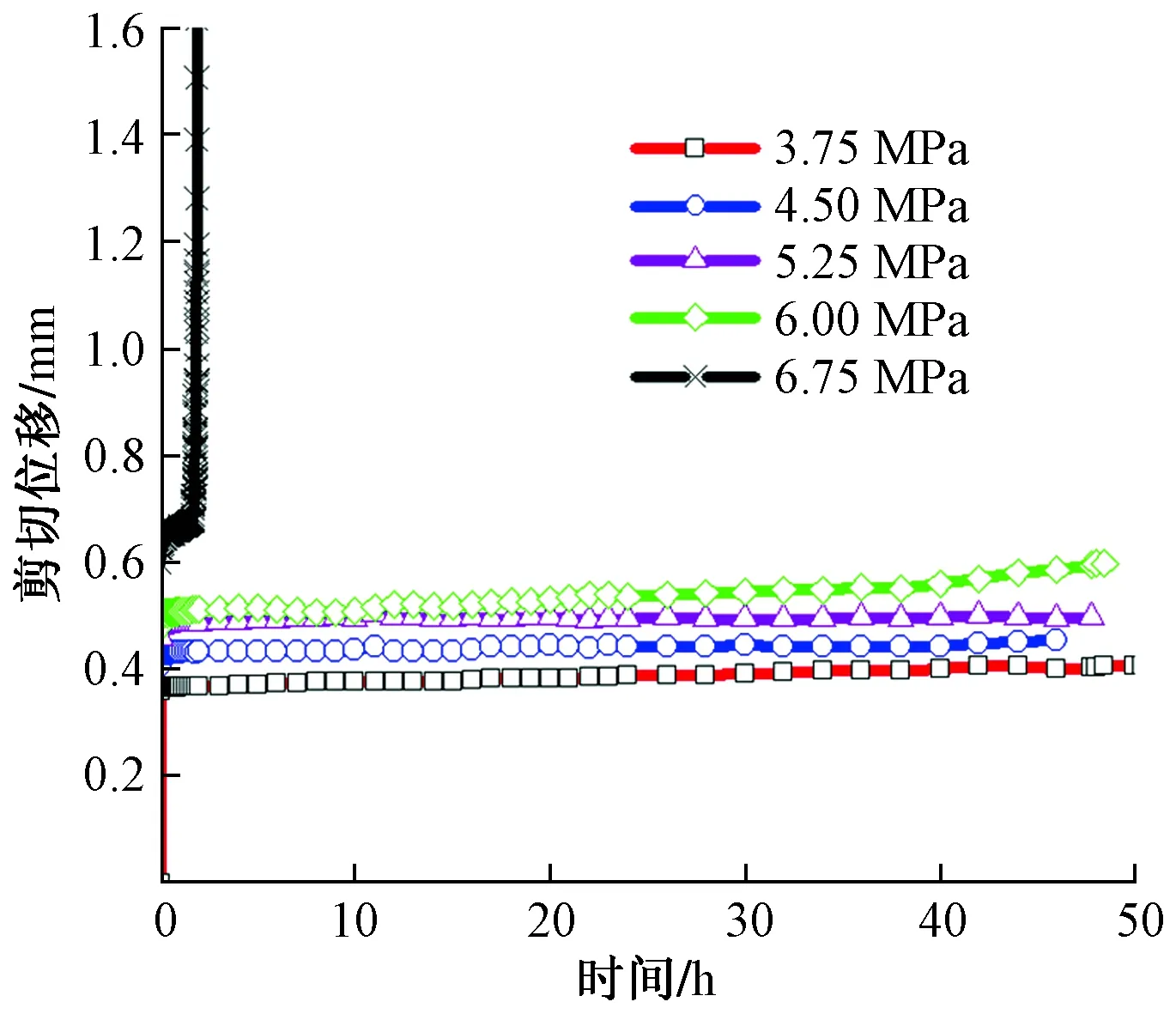
图2 剪切流变试验曲线Fig.2 Shear rheological test curve

2 分数阶微积分软体元件

2.1 分数阶微积分简介

分数阶微积分的定义方式多样,而最常用且应用广泛的定义方式为Riemann-Liouville。分数阶微积分核心在于将整数阶微积分推广至分数、复数层面。

函数f(t)的β阶积分为[9]

(1)

式(1)中:t、t0、τ为自变量；β为阶数。

分数阶微分定义为

(2)

式(2)中:β∈(n-1,n],n为正整数,且β>0；Γ(β)为Gamma函数,即

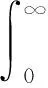
(3)

式(3)中：Re代表取复数的实部。

2.2 基于分数阶微积分建立的软体元件

实际上,岩石为一种介于理想弹性体和理想流体之间的一种流体材料。

理想弹性体(Hooke体)的应力σ与应变ε之间呈正比例关系，即

(4)

式(4)中:τ为应力,MPa；ε为应变；E为弹性模量,GPa。经过改写可以写为[2,9,13]

(5)

理想流体(Newton体)应力-应变-时间关系为

(6)

式(6)中:η为黏性系数；t为时间。经过改写可以写为[2,9,13]

(7)

由于岩石材料在黏弹性阶段既非理想弹性体也非理想流体的性质,恰好与式(5)、式(6)中的微分阶数0和1相对应,因此其岩石的本构关系可能为

(8)

式(8)中：β指元件阶数,β=0或1时,正好对应于理想状态下的弹性体和流体。因此,该软体元件(图3)可应用于岩石材料变形的描述。

图3 软体元件Fig.3 Software element

当应力τ恒定时,该元件即可用来描述岩土材料的蠕变特性。对式(8)进行分数阶积分,依据R-L分数阶微积分算子理论,可得:

(9)

3 加速蠕变元件的提出

目前针对于加速蠕变过程的本构元件的提出以改进现有的基本元件、基本元件组合、引入M-C(摩尔-库仑)塑性体元件来对加速蠕变过程进行模拟。

张清照等[14]、Zhang等[15]依据结构面剪切蠕变曲线的特点,提出一个非线性黏性元件,如图4所示,以更好地对结构面剪切蠕变全过程进行模拟。

图4 非线性黏性元件Fig.4 Nonlinear viscous element

非线性黏性元件的应力、应变关系为

(10)

即非线性黏性元件的本构模型为

(11)

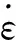
当岩石应力达到屈服应力条件下,岩石蠕变开始进入加速蠕变阶段。此时,蠕变应变速率开始快速增长,黏壶元件黏滞系数开始逐渐降低,依据Jean Lemaitre[8,16]应变等价性假说,对式(11)中的η进行非定常化,加速蠕变元件经非定常化之后的本构方程为

(12)

式(12)中：b为与流变有关的参数。

4 蠕变本构模型构建

通过对剪切蠕变试验进行分析,剪切蠕变试验体现了瞬时变形、衰减蠕变过程、稳速蠕变过程、加速蠕变过程。根据此试验现象,建立了一个由弹簧元件、黏弹性元件、一个能够反映加速蠕变过程的非线性黏性元件通过串并联的方式组成基于分数阶微积分的岩石硬性结构面蠕变本构模型,如图5所示。

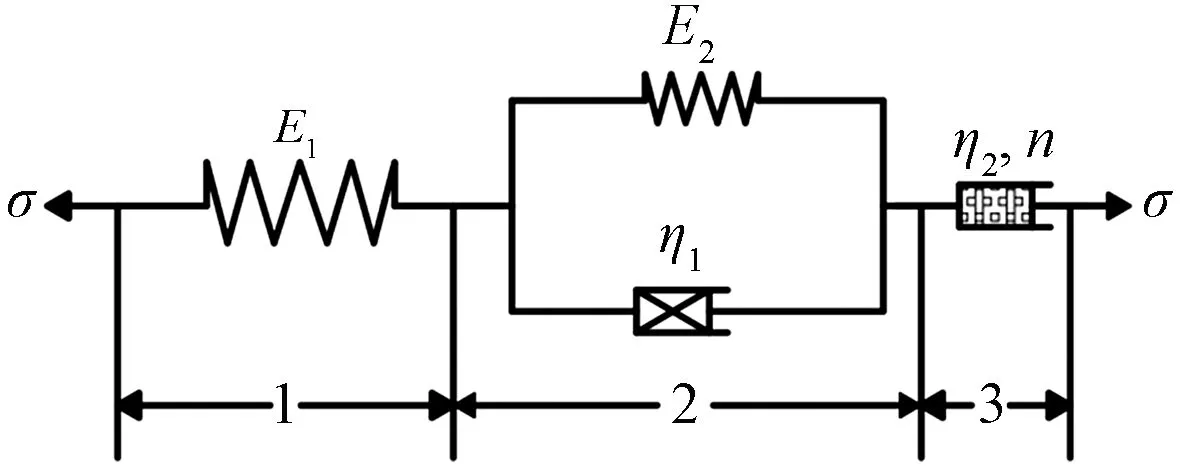
图5 基于分数阶微积分蠕变本构模型Fig.5 Creep constitutive model based on fractional calculus

由本构模型的并联型关系可知,图5中本构模型的总应变等于图中1、2、3部分的总和,即

ε=ε1+ε2+ε3

(13)

(1)弹性体(胡克体)的应力-应变关系满足Hooke定律,其应力-应变关系应满足:

(14)

(2)分数阶微积分Kelvin体中含基于分数阶微积分所建立的软体元件,能够更好地对岩石的黏弹性变形过程进行模拟,其应力-应变关系应满足:

(15)

式(15)中：εve、εe、ε分别为Kelvin体、Kelvin体中弹性元件、Kelvin体中黏性元件所产生的应变。

将式(8)和式(14)代入式(15),可得黏弹性体的应力-应变-时间关系为

(16)

经过转换,即可得：

(17)

对式(17)进行拉普拉斯变换后可得

(18)

式(18)中：s表示拉普拉斯变换空间复变量。

假设,τ/η1=a,E2/η1=b,代入式(18)并整理得：

(19)

进一步通过对式(19)进行拉普拉斯的逆变换,即可得出：

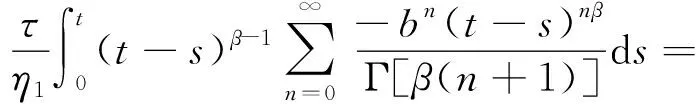
(20)

(3)模型加速蠕变元件的本构模型为

(21)

式(21)中：λ的意义与式(12)中n的意义相同。

根据本构模型总应变与各元件之间的应变关系,即式(14),得所用的本构模型为

(22)

式(22)中：第1式适用范围为在岩石蠕变过程未出现加速蠕变阶段的过程；第2式适用于在岩石蠕变过程中出现加速蠕变阶段的岩石蠕变。

5 模型参数辨识及验证

对模型参数辨识及验证主要采用1stOpt数学优化软件,基于麦夸特法M-L算法和通用全局算法,利用不同条件下蠕变试验数据对上述本构模型中的参数进行拟合,拟合参数如表2所示。通过分析本构模型中待定参数,若岩石蠕变过程未出现加速蠕变阶段时,其所需拟合的参数量为5个,分别为E1、E2、η1、β、n；若岩石蠕变过程出现加速蠕变阶段,其所需要拟合的参数量为8个,分别为E1、E2、η1、η2、β、n、b、λ。总体上,模型中所需拟合的参数相比较于现有的多数模型参数减少,同时根据R2,试验数据与本构模型之间的相关性较高。

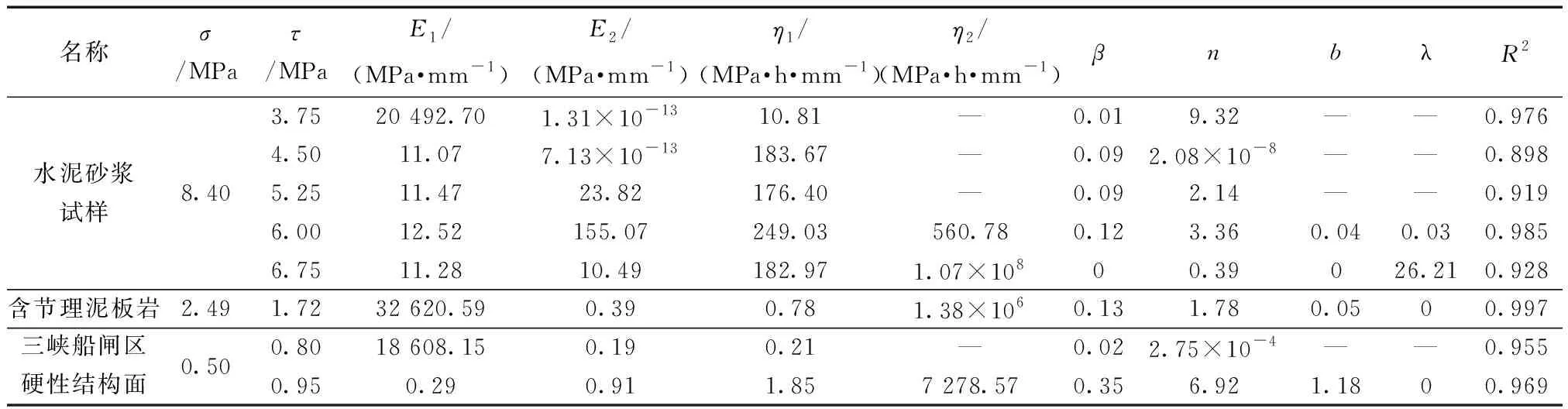
表2 硬性结构面蠕变本构模型参数

注:拟合参数小于1×10-10时取为0。

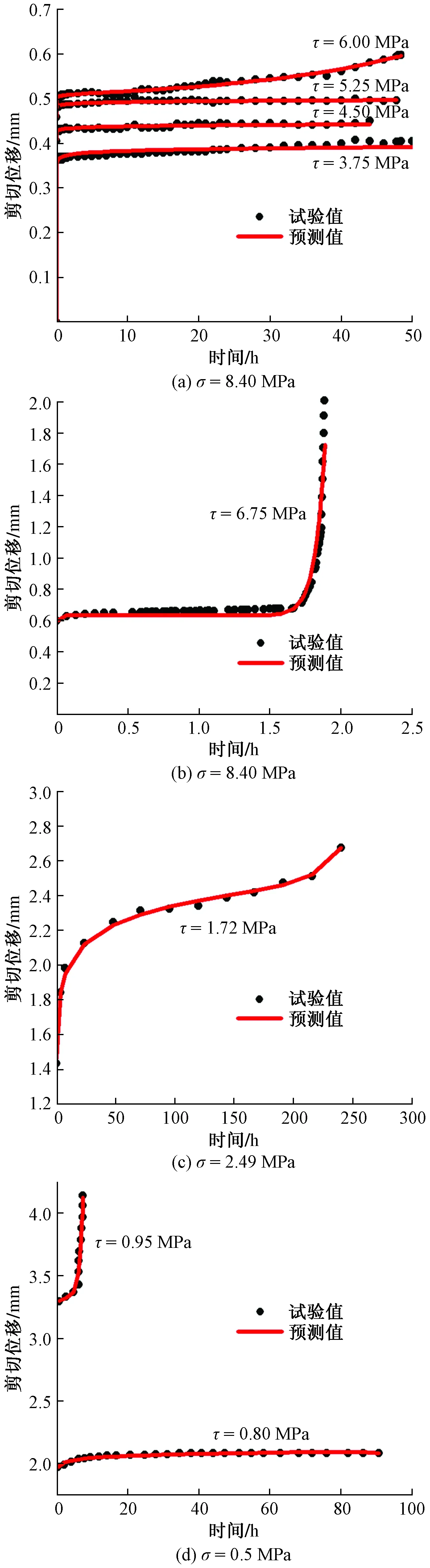
图6 蠕变试验值与预测值对比Fig.6 Comparisons between creep test values and predicted values

图6(a)、图6(b)所示为结构面连通率k=0.64、σ=8.40 MPa下剪切蠕变试验与拟合值对比。对比非贯通结构面岩样的剪切蠕变试验值与预测值,本文中的本构模型能够较好地对非贯通结构面剪切蠕变特性的3个阶段进行模拟,之间的平均相关性系数R2为0.94。图6(c)、图6(d)分别为利用本文所建本构模型对文献[1,17]中贯通型硬性结构面岩石的蠕变试验数据进一步验证,最终通过比较试验值与拟合值,表明本构模型能够较好地对蠕变的3个阶段进行模拟,之间的平均相关性系数R2为0.97,说明本文所构建基于分数阶微积分的岩石硬性结构面蠕变本构模型也可适用于贯通型硬性结构面。经过对所建本构模型的验证,本构模型能够较好地反映出含硬性结构面岩样(岩体)的蠕变特性。

6 结论

通过元件组合方式构建适用于岩石含硬性结构面蠕变本构模型,在传统Kelvin模型中引入基于分数阶微积分的软体元件,同时引入一种能够描述结构面蠕变的加速元件,将加速蠕变元件的黏滞系数进行非定常化,构建基于分数阶微积分的岩石硬性结构面蠕变本构模型。

通过连通率k=0.64、σ=8.40 MPa、不同剪应力下的剪切蠕变试验数据对所构建的本构模型进行辨识,结果表明,构建的本构模型能够较好地对非贯通硬性结构面岩体剪切蠕变特性的3个阶段进行模拟,其平均R2为0.94左右。

利用含节理泥板岩及三峡船闸区岩石的贯通型硬性结构面试样的蠕变试验数据,进一步对本文所建的本构模型进行验证,结果表明,本构模型能够较好地对贯通性结构面的试验数据进行辨识,其平均R2为0.97。

综上,本文所构建基于分数阶微积分的岩石硬性结构面蠕变本构模型能够较好地反映含硬性结构面岩体的蠕变特性。