冻融循环下隧道围岩冻胀力理论计算

刘红岩，赵雨霞

(1. 中国地质大学(北京)工程技术学院，北京，100083；2. 国土资源部深部地质钻探技术重点实验室，北京，100083)

冻融造成的岩体工程失效是目前寒区工程建设中常常遇到的问题，如围岩冻胀引起的隧道衬砌开裂被认为是寒区隧道破坏的主要形式之一[1-2]。围岩冻胀力计算是寒区隧道建设的前提和基础。岩体孔隙及裂隙中的水在低温下发生冻结，将产生巨大的冻胀力[3]，导致岩体发生进一步损伤。而后融化后的水又进入新形成的裂隙中，如此循环往复。多次冻融循环将导致岩体发生一系列物理变化，最终引起隧道衬砌开裂。为此许多学者从试验、理论及数值计算等多个方面对其进行深入地研究。首先，在试验研究方面，渠孟飞等[4]采用室内模型试验研究水在裂隙中迁移产生的冻胀力，认为衬砌冻胀力在仰拱和仰拱脚处较小，边墙处最大，而拱顶和拱脚居中；HU 等[5]通过室内模型试验研究隧道衬砌结构上的冻胀力分布特征；仇文革等[6]通过室内试验研究在不同约束及冻结深度下，寒区裂隙岩体隧道中的冻胀力分布规律，发现冻结深度越深、顶部约束越强，隧道围岩的冻胀力就越大。其次，在理论研究方面，赖远明等[7]基于黏弹性相应原理求得寒区隧道的冻胀力和衬砌应力；张全胜等[8]基于弹性理论提出隧道围岩冻胀力计算方法，并采用复变函数法得到了冻融后隧道衬砌所受冻胀力计算公式；刘泉声等[9]基于弹性力学、渗流和相变理论建立考虑水分迁移下的单裂隙冻胀力求解模型，认为冻胀力不仅随着水分迁移通量增加而快速减小，而且还与岩石基质及冰体的力学参数有关。最后，在数值计算方面，TAN等[10-11]基于连续介质力学、热动力学及分凝势理论分别建立岩体温度-渗流(TH)耦合模型及温度-渗流-应力-损伤(THMD)耦合模型，并开发了相应的有限元数值计算程序，应用于某隧道的冻胀计算。理论角度研究岩体及隧道围岩冻胀力是从根本上掌握隧道冻融破坏本质的主要途径之一，然而尽管目前已经取得较丰硕的研究成果，但是仍存在一定的问题。如前述理论计算模型[7-9]仅考虑单次冻胀条件下的围岩冻胀力，没有考虑围岩冻胀力随冻融循环次数的变化规律。而隧道等实际岩体工程在服务年限内均会经历多次冻融循环，也将不可避免地对岩石造成冻融损伤。考虑岩石冻融循环损伤对围岩冻胀力的影响则是目前亟待解决的一个重要问题。有学者已开始对该问题进行初步研究，如LIU等[12]建立考虑冻融循环引起的岩石损伤对围岩冻胀力影响的理论模型。但是该研究仍存在3 个方面的问题需要进一步深入研究：1)在冻胀力弹性理论计算中，仅考虑冻结围岩向衬砌方向的膨胀变形，而未考虑其向未冻结围岩区的膨胀变形；2)在计算岩石冻融损伤时，假设每次冻胀引起的微裂纹扩展长度都相等；3)关于岩石冻胀率的计算，认为冻融前后岩石的纵波波速不变，然后得到相应的孔隙率计算公式。由于冻融造成的损伤，岩石经历冻融循环后，其纵波波速必然会发生变化。为此，针对上述问题，本文作者首先阐述前人提出的基于弹性理论的围岩冻胀力计算方法，而后结合损伤断裂理论研究冻融循环对岩石造成的损伤，即获得岩石弹性模量随冻融循环次数的劣化规律，最终提出考虑岩石冻融循环损伤的隧道围岩冻胀力计算方法。

1 基于弹性理论的围岩冻胀力计算

图1 所示为文献[8]的隧道围岩冻胀力计算模型，即将隧道衬砌和围岩中的冻结区及未冻结区看成是由3个轴对称弹性体相互完全接触组成的受力体系，其中隧道为位于无限大山体中的圆形孔，a，b和c分别为衬砌内径、冻结区内径(亦为衬砌外径)和冻结区外径，并做如下假设：1)围岩为均质、各向同性的连续介质；2)隧道衬砌及围岩受力属于弹性力学的平面应变问题；3)冻结区始终处于饱和状态；4)不考虑围岩及隧道衬砌的自重。

设冻结围岩发生冻胀时向衬砌方向及未冻结围岩方向上发生的冻胀位移分别为Δh1和Δh2。σf和σh分别为由冻结围岩作用在衬砌及未冻结围岩上的冻胀力，这里主要关注作用在衬砌上的冻胀力σf。对衬砌而言，其可视为仅受外压及冻胀力作用的厚壁圆筒，即为典型的轴对称问题。因此，可以采用极坐标求解。根据弹性理论[13]，在冻胀力σf作用下，隧道衬砌的径向位移u1(r)如下(其环向位移为零)：式中：E1和υ1分别为衬砌弹性模量与泊松比；r为模型中任一点到隧道中心的距离。

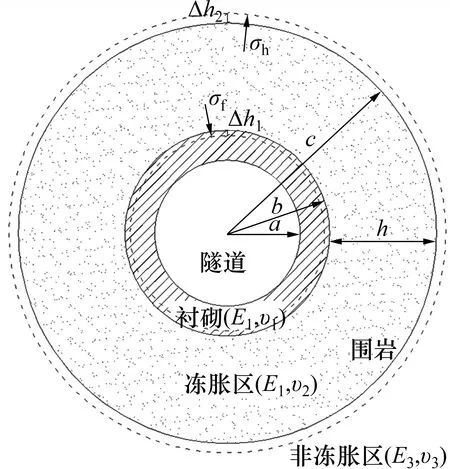
图1 隧道冻胀力计算模型Fig.1 Calculation model of tunnel frost heaving pressure

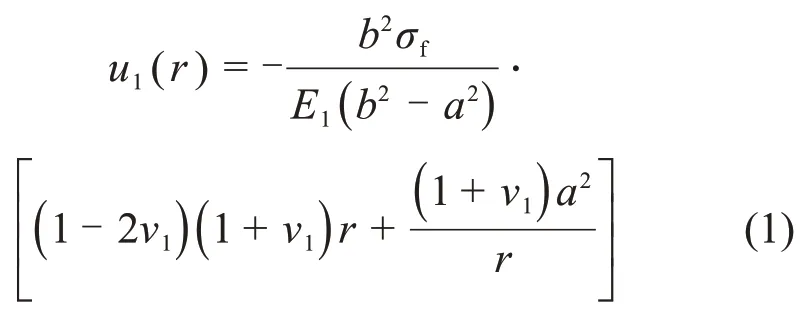
在衬砌外径处，即r=b时，其位移δ1为

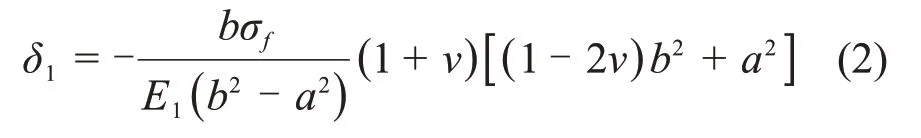
冻结围岩可视为同时受内压σf及外压σh作用的轴对称问题，由此可得其位移u2(r)为[13]

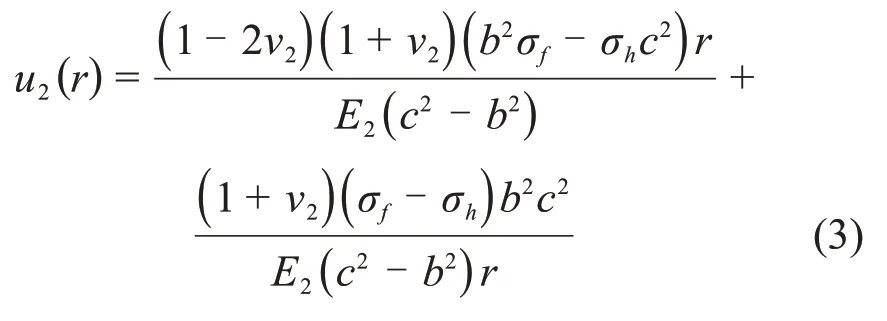
式中：E2和υ2分别为冻结区岩石弹性模量与泊松比。

在冻结区内壁处，即r=b，其位移δf1为

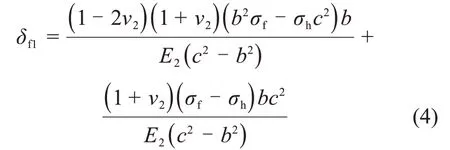
而在冻结区内壁处，即r=c，其位移δf2为

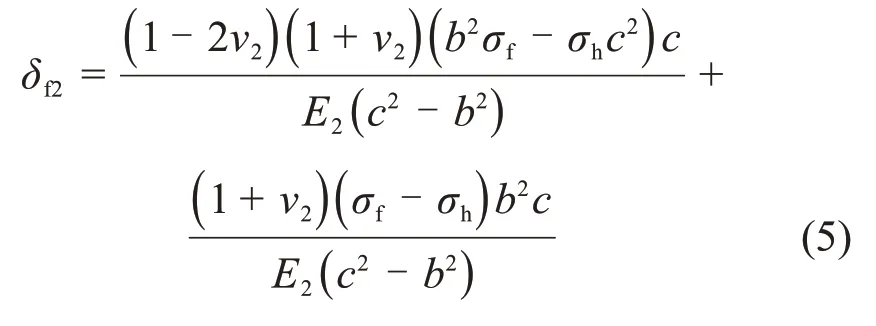
而未冻结围岩可视为仅在内壁受σh作用的轴对称厚壁圆筒，由弹性理论可得其内壁位移δ2为[13]

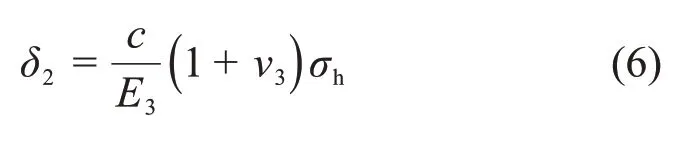
式中：E3和υ3分别为未冻结岩石弹性模量与泊松比。

根据位移连续性条件，在衬砌与冻结围岩的接触面及冻结区与未冻结区的接触面应满足

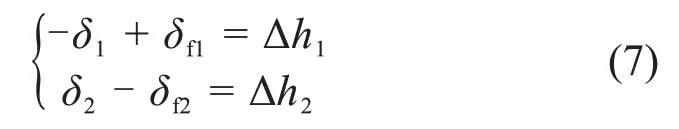
由此可得围岩冻胀力σf为

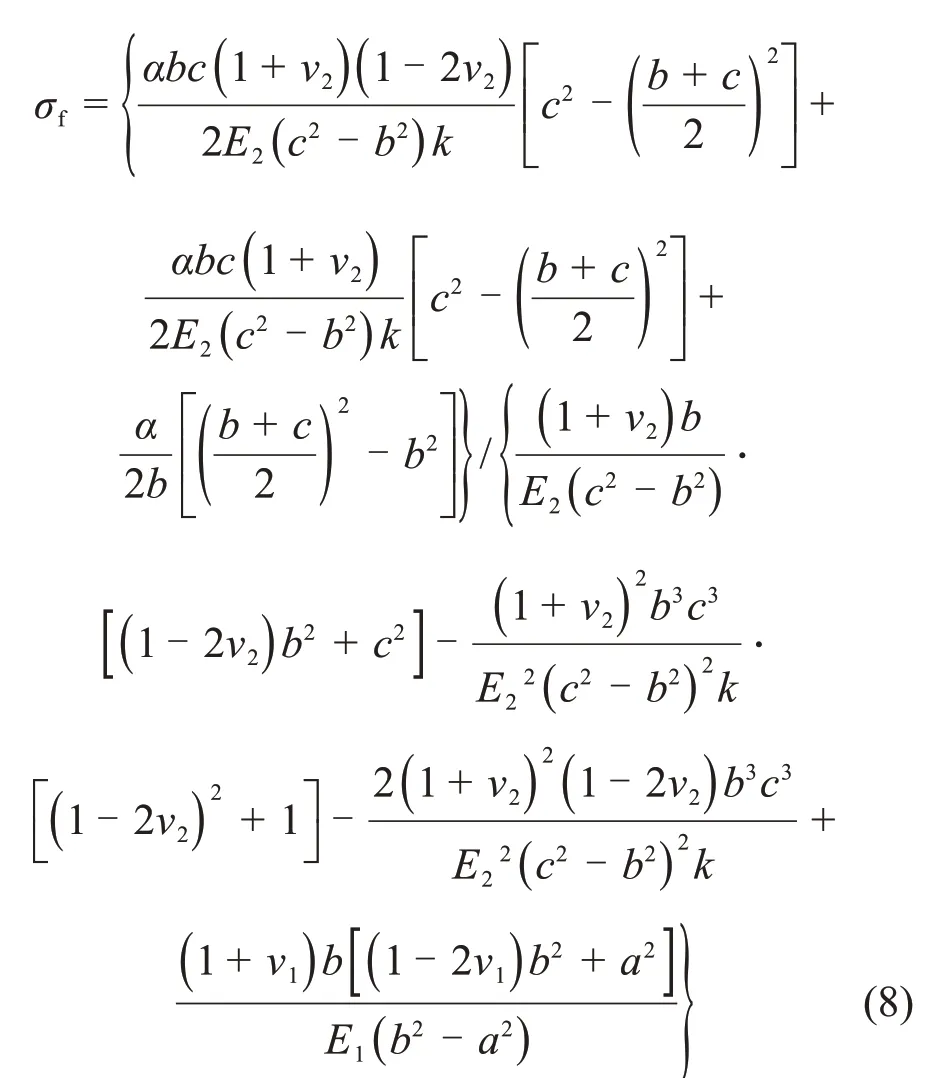
式 中 ：。

由式(8)可知：围岩冻胀力不仅与模型几何尺寸如衬砌内径a、冻结区内径(亦为衬砌外径)b和冻结区外径c有关，而且与模型弹性常数如衬砌弹性模量与泊松比(E1和v1)、冻结岩石弹性模量与泊松比(E2和v2)和未冻结岩石弹性模量与泊松比(E3和v3)有关，更重要的是还与围岩冻胀率α有关。前2类参数均较容易确定，这里不再重述，下面重点探讨冻胀率的确定方法。

冻胀率是岩石冻胀性的定量描述，MATSUOKA[14]对饱和岩石的冻结试验表明：岩石冻胀率受孔隙水冻结后的体积膨胀、水热迁移作用及岩石对冻胀的约束作用等因素的共同影响，多种不同类型岩石的冻胀率为0.1%～0.5%[14]。考虑水热迁移作用对岩石冻胀率的影响，夏才初等[15]提出开放条件下饱和岩石冻胀率的计算公式

式中：η为水热迁移影响系数，冻胀敏感性岩石取1.58，非冻胀敏感性岩石取1.00；n为岩石孔隙率。

2 冻融循环下围岩弹性模量

2.1 单条微裂纹在冻胀力作用下的起裂及扩展方向

每一次冻融循环都将对岩石造成一定程度的损伤，在细观上则表现为微裂纹长度增加，而在宏观上则体现为弹性模量降低。为此，从细观力学角度，研究冻融循环对岩石弹性模量的影响，提出考虑损伤的隧道围岩冻胀力计算方法。

将岩石中的微裂纹视为平面状态下的扁平状椭圆裂隙，如图2所示，椭圆长轴2l，短轴2t，且t＜＜l。

微裂纹内壁受到均匀的法向冻胀力p作用，经过N次冻融循环后，微裂纹半长变为lN，假设微裂纹沿着应变能密度因子最小的方向扩展，即微裂纹的失稳扩展是由于最小应变能密度因子Smin达到材料相应的临界值Sc时发生，在平面应变条件下，纯I型微裂纹尖端区域应变能密度场强度S为[16]

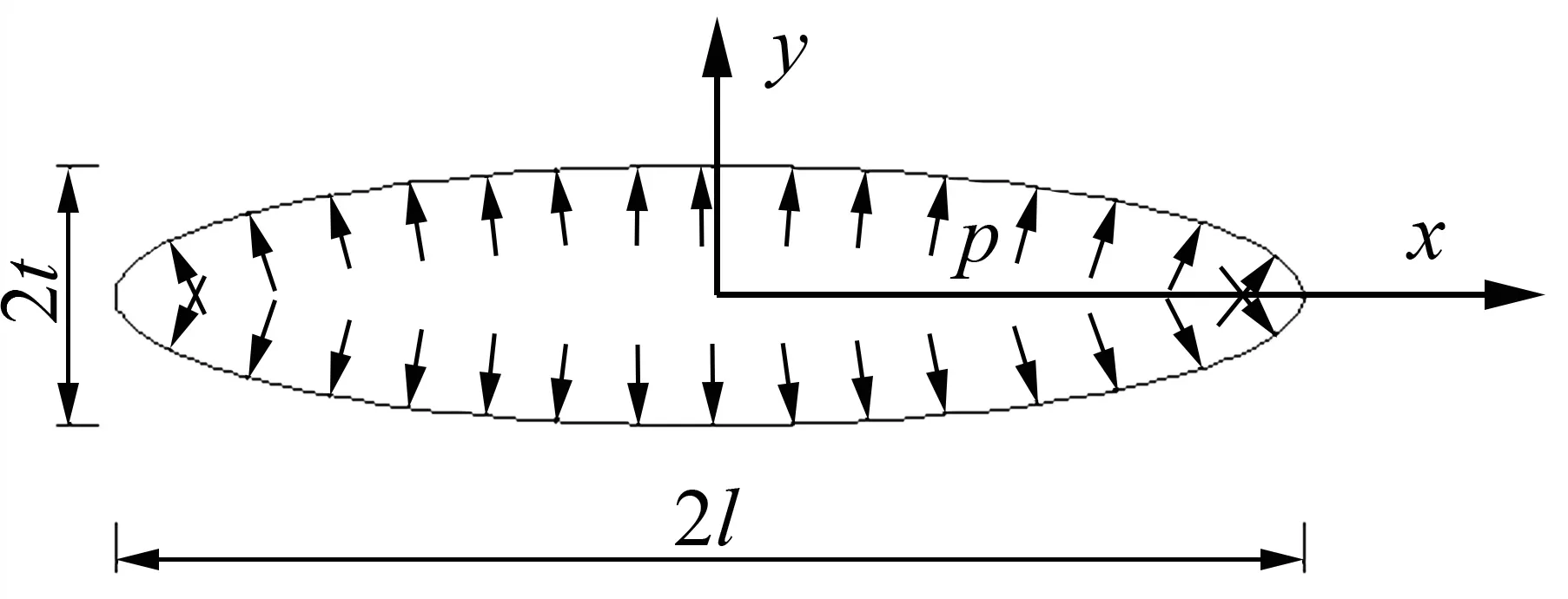
图2 冻胀力作用下的微裂纹模型Fig.2 Microcrack model under frost heaving pressure

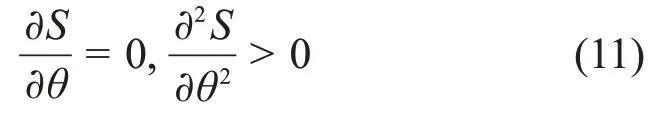
由式(11)可以确定翼裂纹起裂角θ= 0，即微裂纹发生自相似扩展。

微裂纹起裂判断依据为

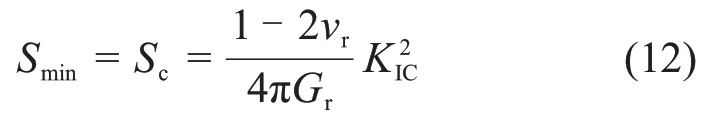
式中：KΙC为岩石断裂韧性。

2.2 单条微裂纹在冻胀力作用下的扩展长度

当微裂隙发生冻胀作用时，其内壁将作用均匀分布的冻胀力相应地微裂纹将向x和y这2 个方向扩展，如图3所示，在研究微裂纹冻胀扩展时进行以下假设[17]：1) 冻胀前后微裂纹均为平面椭圆形，即形状不变和中心位置不变，仅大小发生变化；2)忽略水分迁移与岩石骨架变形；3)微裂纹始终饱和；4)微裂纹稳定扩展，且符合线弹性断裂理论。

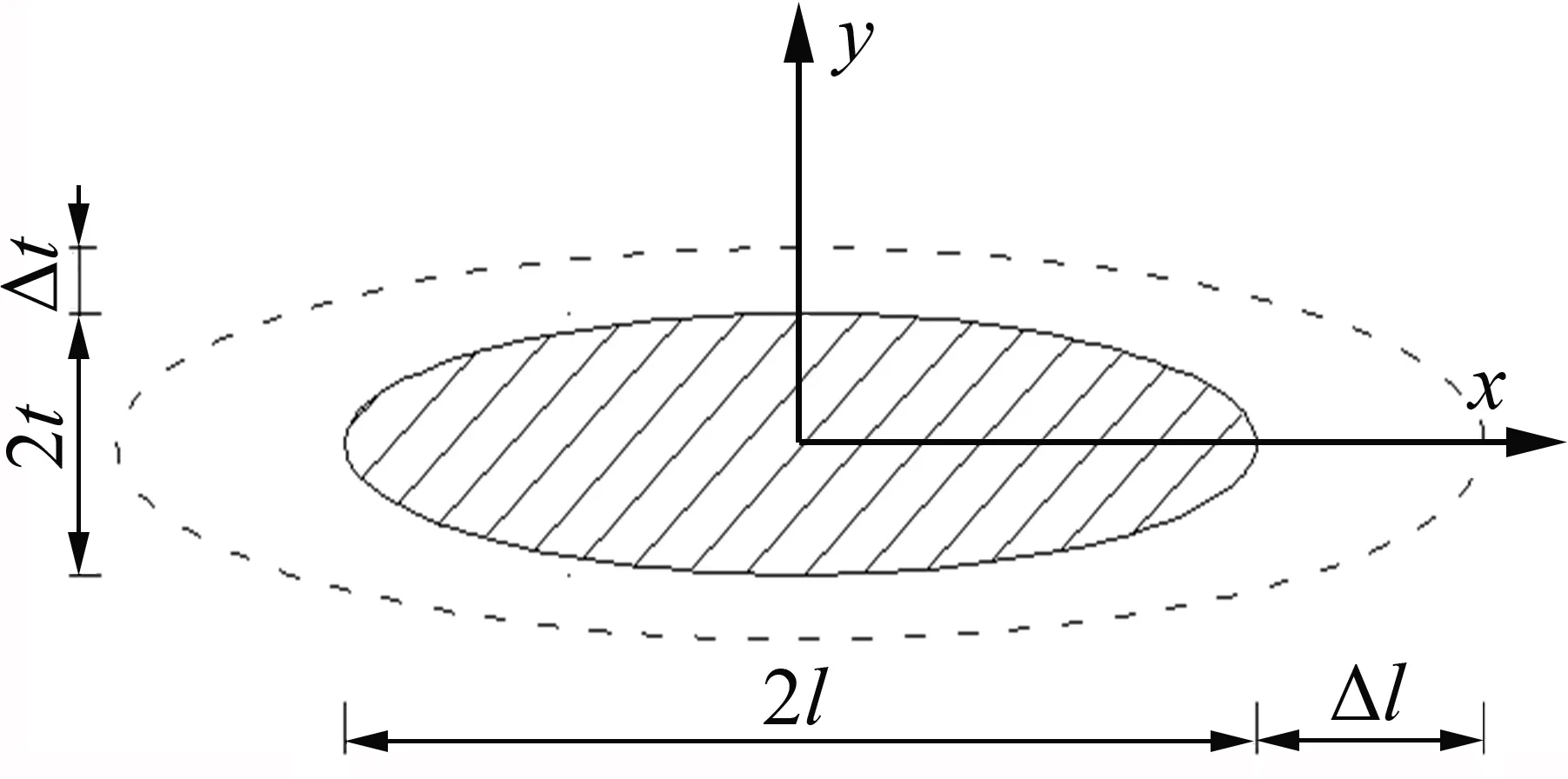
图3 微裂纹冻胀扩展模型Fig.3 Frost heaving propagation model of microcrack

根据Griffith 能量释放率理论，当微裂纹中的水冻结成冰时，体积膨胀，但是由于微裂纹面的束缚，冰体对其产生膨胀压力，在微裂纹周围介质中将产生弹性应变能。当微裂纹尖端应力强度因子K1大于断裂韧度K1c时，微裂纹开始扩展，弹性应变能释放，因而有

式中：W为冻胀力做的功；Z为微裂纹周边储存的弹性应变能；U为整个系统下降的总势能。

假设微裂纹扩展时弹性应变能全部释放，则

当应力强度因子大于等于断裂韧度时，微裂纹开始扩展，则扩展后的微裂纹形态如图3中的虚线所示。此时冻胀力沿微裂纹壁面法向做功，故式(14)左边可表示为

式(14)右边的系统势能降低可用扩展力做功表示为

式中：Y为微裂隙Griffith能量释放率，

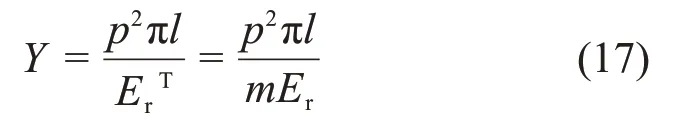
把式(15)～(17)代入式(14)可得

根据微裂纹中的水发生相变前后微裂纹的体积变化，可得

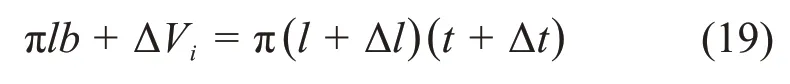
由式(18)～(19)可得到关于微裂纹扩展长度的方程为

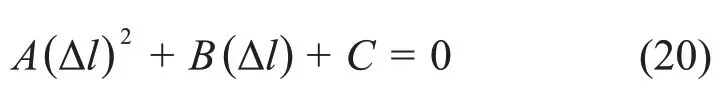
式中：A= πY；B= π(2plt+lG)；C= -2plΔVi。

对式(20)进行求解可得平面应变条件下裂纹扩展长度与冻胀应力之间的关系式：

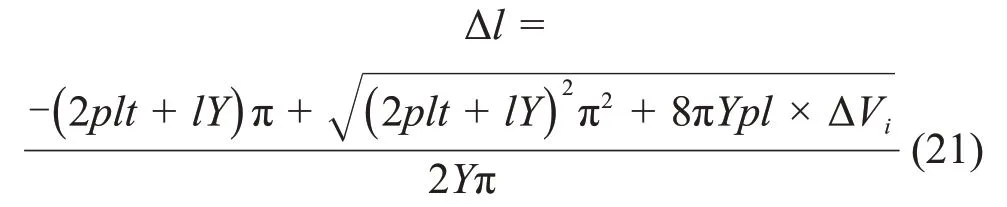
当采用式(21)求解时，需要确定冰体单宽膨胀体积ΔVi及冰对微裂纹壁的膨胀压力p。

首先，讨论ΔVi的计算方法。若不考虑微裂纹面的束缚，微裂纹中的冰体将发生自由膨胀，但是在实际情况下，微裂纹壁将对冰体施加大小为p的反作用力，冰体产生弹性应变。根据弹性理论，在平面应变条件下冰的体应变εv为

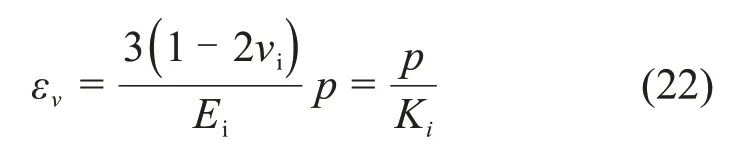
其中：Ei，υi和Ki分别为冰的弹性模量、泊松比与体积模量。

假设冰在自由膨胀时，其体积膨胀率为9%，在膨胀压力为p时的微裂纹体积变化为

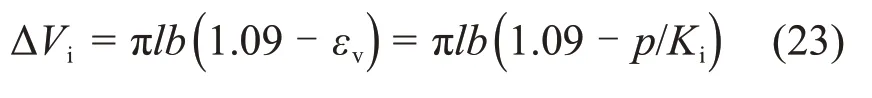
其次，讨论单条微裂纹冻胀力p的计算方法。由图3可知：由于膨胀后微裂纹将发生改变，而形状保持不变，因此可设

结合式(18)和(24)可得

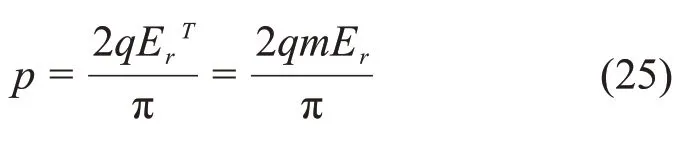
将式(17)，(23)，(25)代入式(21)可得

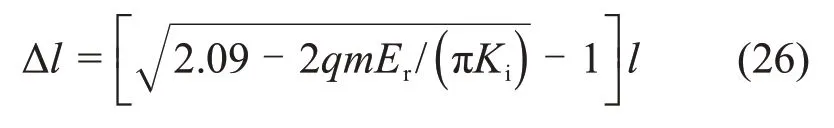
2.3 岩石弹性模量与冻融循环次数的关系

基于细观损伤理论，采用平均化方法，把上述的细观损伤力学研究结果反映到材料的宏观力学性能中，这里采用Mori-Tanaka 方法[19]，在二维条件下，考虑微裂纹之间的互相作用，可得到岩石有效弹性模量的表达式为

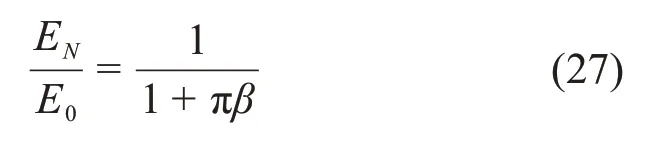
式中：E0为岩石初始弹性模量，MPa；EN为冻融N次之后的岩石等效弹性模量，MPa；β为微裂纹密度参数，β=ρ(Δl)2；ρ为单位面积上经冻融后扩展半长为Δl的微裂纹数量，条/m2。

由于假设微裂纹始终饱和，第N次冻融循环而导致的微裂纹扩展半长ΔlN为

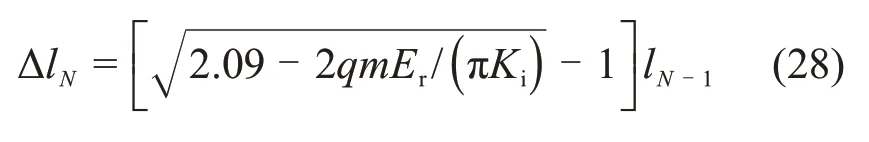
经过N次冻融循环后，微裂纹扩展半长lN为

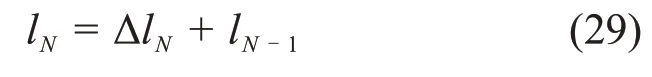
经过N次冻融循环后，微裂纹密度参数β可表示为

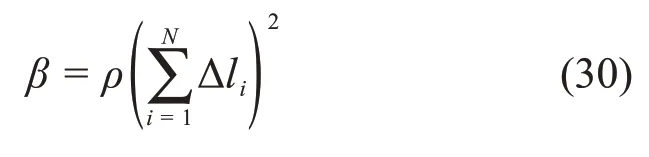
ROSTÁSY 等[20]认为岩石经过多次冻融循环后，微裂纹总数基本没有增加，只是长微裂纹发生扩展，而短微裂纹由于受到其他微裂纹的挤压而闭合。即随着冻融循环，能够持续扩展的微裂纹数目将越来越少。根据Griffith微裂纹传播理论，单位体积内被激活扩展的微裂纹数量服从指数分布，即

式中：ρ0为微裂纹总数；lc为微裂纹分布参数。

把式(28)～(31)代入式(27)可得

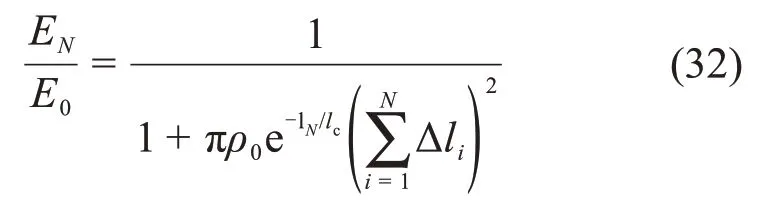
由式(32)即可求得N次冻融循环后岩石弹性模量EN。为了验证计算方法的正确性，与TAN 等[21]的试验结果进行对比，试验所用岩石为取自西藏嘎隆拉山区的花岗岩，制作成直径为50 mm、高为100 mm 的圆柱形试件。其物理力学参数为：干质量及饱和质量分别为521.87 g 和523.13 g，干密度为2.77 g/cm3，单轴压缩峰值强度为135.73 MPa。表1所示为计算参数，依表1可求得其弹性模量随冻融循环次数N的变化规律如图4所示。由图4可见：随着冻融循环次数增加，岩石弹性模量逐渐降低，且降低速度随着冻融循环次数的增加而逐渐减小，与试验结果吻合较好。

3 冻融循环下围岩冻胀力的损伤力学解答式

冻融循环会对岩石造成不同程度损伤，导致岩石弹性模量降低。而在对围岩冻胀力的计算即计算式(8)是按照弹性理论计算的，没有考虑冻融循环后岩石弹性模量的降低及孔隙率增加，因而仅适合于求解围岩的初次冻胀力。实际岩石工程往往是在工程服务期内经历多次冻融循环，因此，这里拟考虑冻融循环对围岩的损伤，提出冻融循环下围岩冻胀力的损伤力学解答式。

假设冻融循环仅对冻结区岩石的力学性质有影响，而对衬砌混凝土及未冻结区岩石的力学性质则没有影响。由式(32)及(8)即可求得第N次冻融循环时的围岩冻胀力σf(N)为

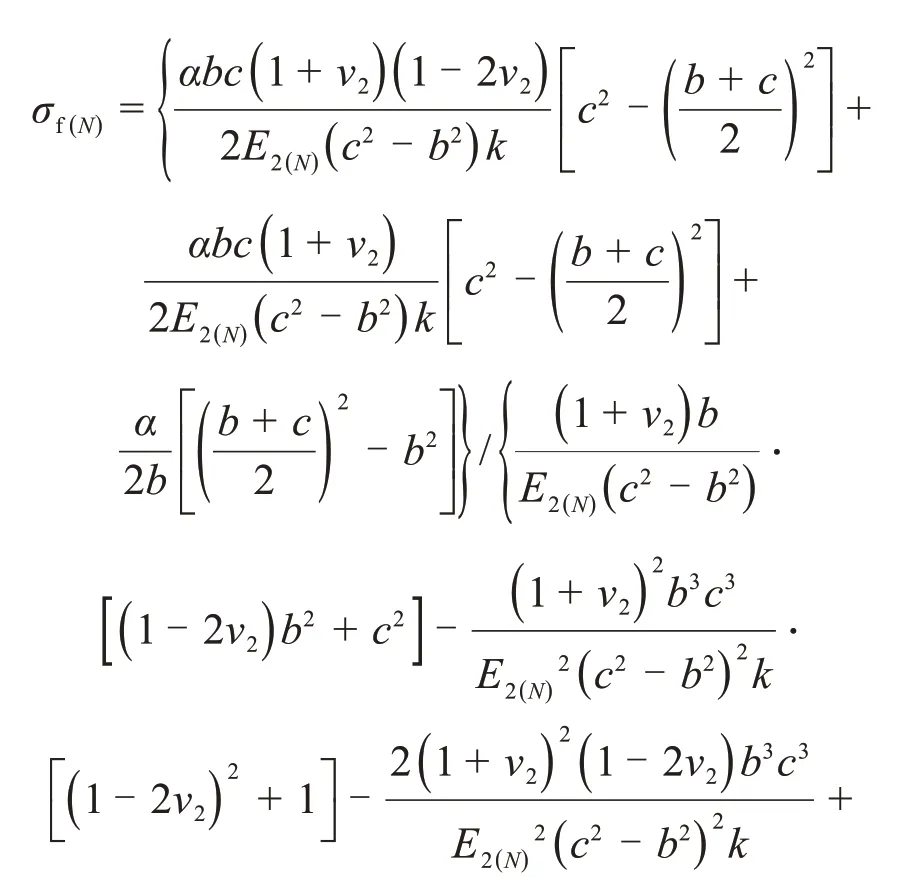
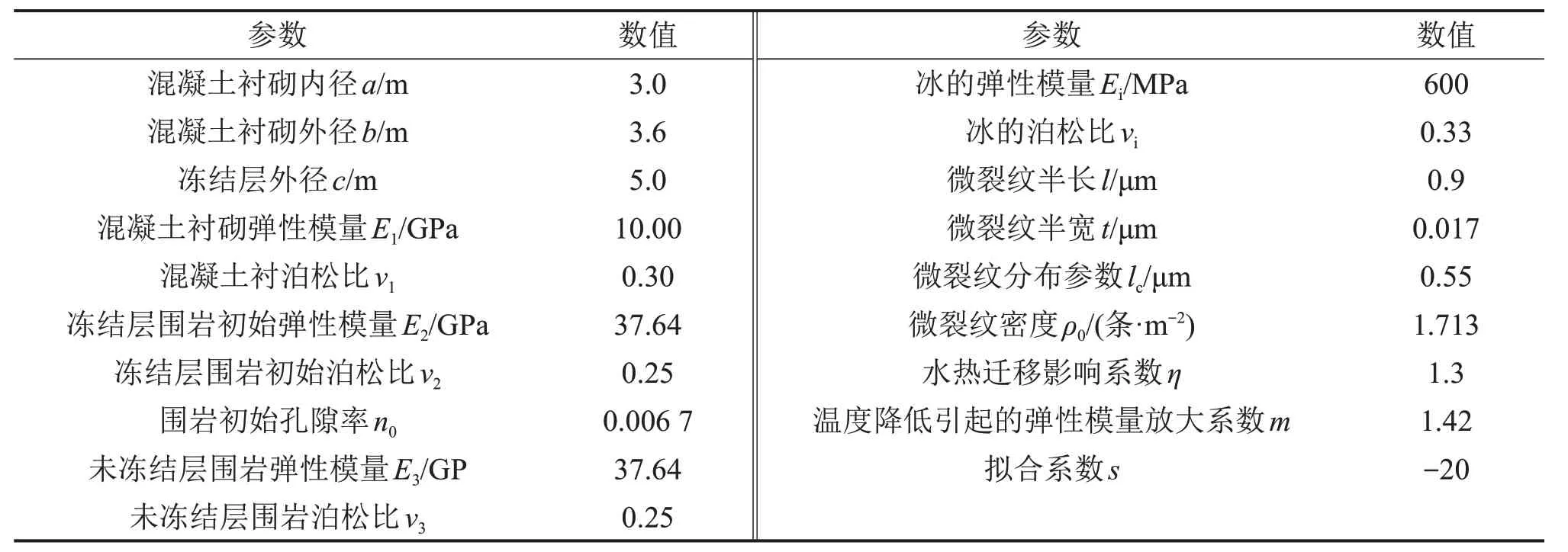
表1 计算参数表Table 1 Calculation parameters

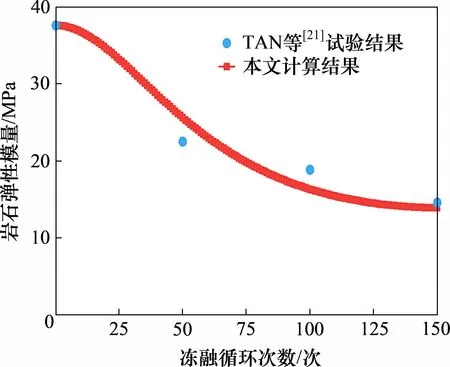
图4 岩石弹性模量随冻融循环次数的变化规律Fig.4 Variation of rock elastic modulus with the number of freeze-thaw cycles

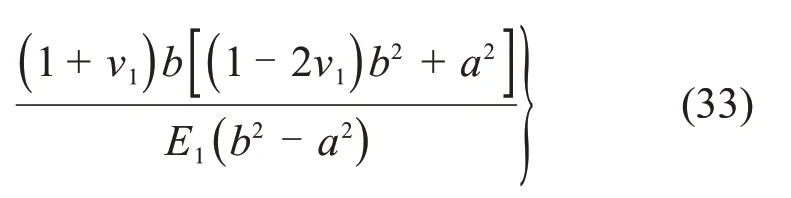
同时，随着冻融循环次数增加，岩石弹性模量降低，与之相对应的物理过程是岩石孔隙率增加，而由式(9)可知，随着孔隙率增加，岩石冻胀率将明显增加，最终对围岩冻胀力产生影响。田延哲等[22]认为在冻融循环作用下，岩石弹性模量随孔隙率的变化规律为

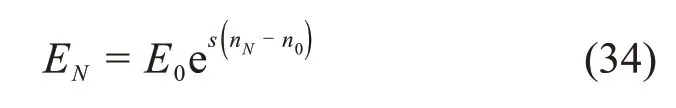
式中：E0和EN分别为岩石的初始弹性模量及经过N次冻融循环后的弹性模量；n0和nN分别为岩石的初始孔隙率及经过N次冻融循环后的孔隙率；s为拟合系数。由式(34)可得

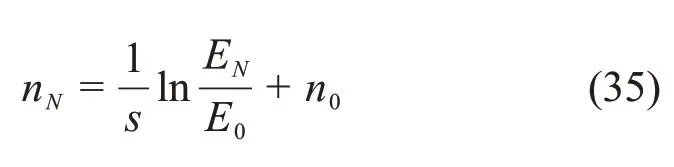
将式(35)代入式(9)可得经过N次冻融循环的岩石冻胀率αN为

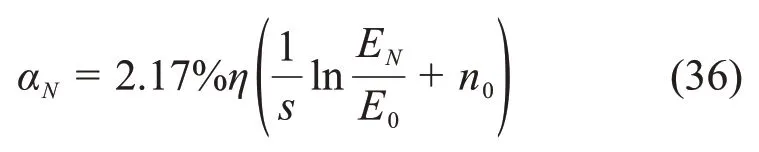
将式(36)代入式(8)即可得到第N次冻融循环时的隧道围岩冻胀力σf(N)为

4 算例与讨论

下面通过算例说明围岩冻胀力随冻融循环次数N的变化规律，设某寒区圆形隧道如图1 所示，计算参数如表1所示。

假定在冻融循环过程中岩石始终饱和。那么可得经过150次冻融循环后，围岩冻胀力σf(N)与冻融循环次数N的变化关系如图5所示。由图5可见：

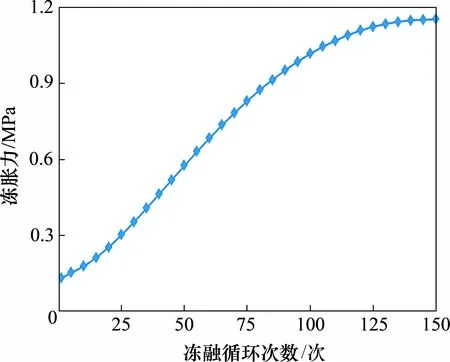
图5 围岩冻胀力随冻融循环次数的变化规律Fig.5 Variation of frost heaving pressure in surrounding rock with the number of freeze-thaw cycles

1)当岩石开始冻胀时，由式(36)可计算得到其冻胀率为1.89×10-4，进而由式(37)可计算得到其冻胀力仅为0.13 MPa。随着冻融循环次数增加，岩石孔隙率增加，其冻胀率也随之增加，最终导致围岩冻胀力增加到1.16 MPa，约为最初冻胀力的8.92倍，增加幅度非常显著。

2)随着冻融循环次数增加，其增长速率逐渐变缓。这是因为岩石冻胀主要是孔隙中的水冻结成冰造成体积膨胀，岩石颗粒因冻结而造成的体积膨胀则几乎可以忽略不计。

3)在初始阶段，岩石孔隙率较小，相应地因冻结而产生的冻胀力也较小，而随着冻融循环，微裂纹在冻胀力作用下发生扩展，导致岩石损伤增加，孔隙率变大。由于假设岩石始终饱和，岩石含水率也将随之增加，将导致岩石冻胀力增加。如此循环，最终引起围岩冻胀力随着冻融循环次数增加而逐渐增大。

4)随着冻融循环次数增加，冻融岩石的弹性模量将逐渐趋于定值(见图4)，此时岩石损伤也将趋于定值，相应地岩石孔隙率及含水率也将趋于定值，最终将导致围岩冻胀力随着冻融循环次数增加而趋于定值。因此，由上述分析可认为岩石冻胀力主要是岩石孔隙中的水冻结成冰而产生的体积膨胀所致。

为证明上述观点，下面假定岩石冻胀率不变，即恒为1.89×10-4，而认为冻融循环仅导致岩石弹性模量降低，由此可得到围岩冻胀力随冻融循环次数的变化规律如图6所示。由图6可见：随着冻融循环次数N由0 次逐渐增加到150 次，围岩弹性模量则逐渐由初始的37.64 GPa 逐渐降低到13.93 GPa，而相应的围岩冻胀力则由初始的0.130 MPa 逐渐增加到0.137 MPa，增加幅度仅为5.38%，相比图5，其变化幅度非常小，这说明仅考虑围岩弹性模量变化对冻胀力计算结果的影响十分有限。因此，认为岩石冻胀力主要是由岩石孔隙中水的冻结膨胀所导致，从工程角度来说，要减少由冻胀引起的围岩破坏，应主要控制水的渗入，即采取相应的截排水措施，防止地下水及地表水渗入到巷道围岩中。

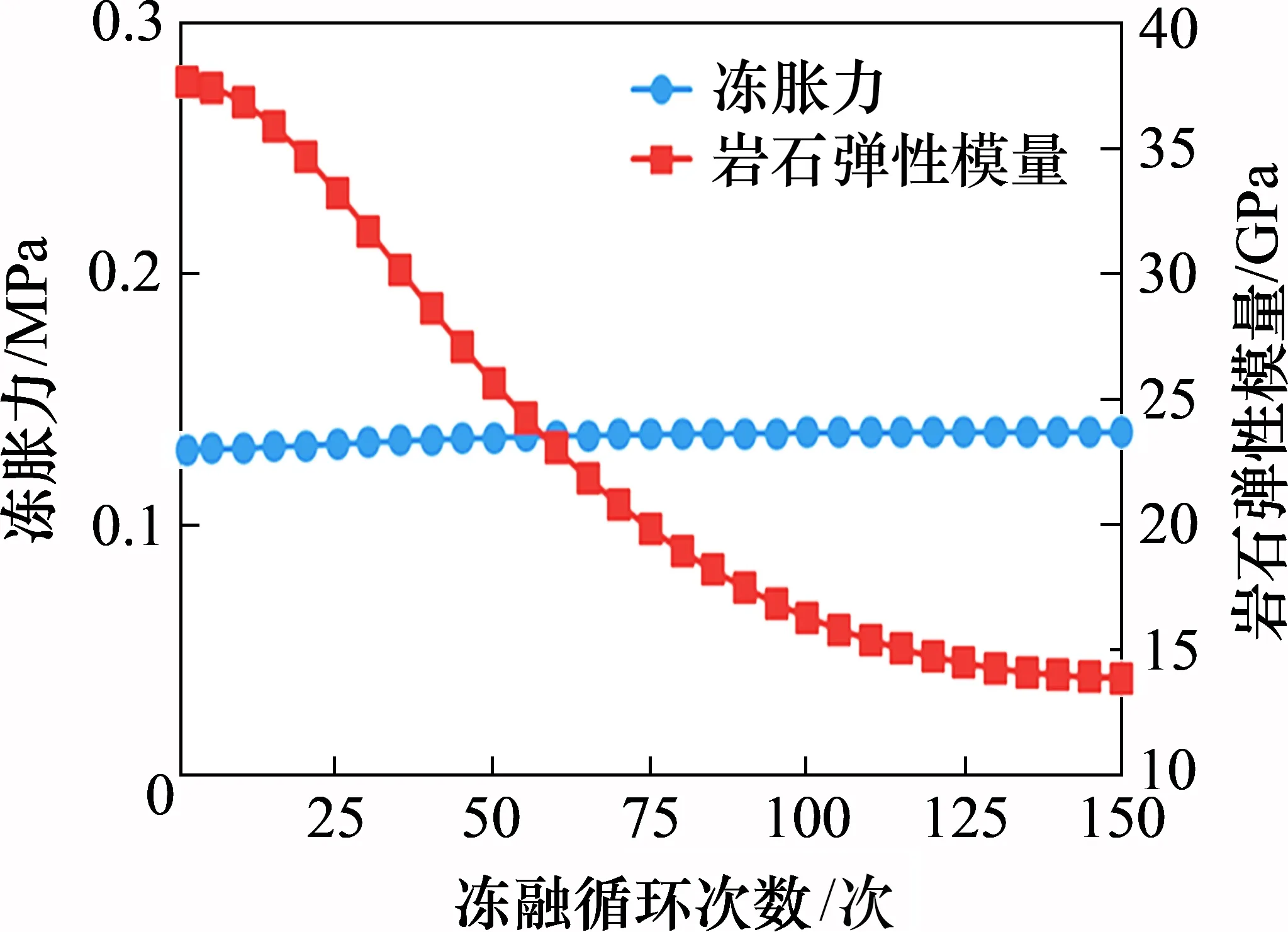
图6 围岩冻胀冻率不变时的冻胀力及弹性模量随冻融循环次数的变化规律Fig.6 Variation of frost heaving pressure and elastic modulus with the number of freeze-thaw cycles when the surrounding rock’s frost heaving ratio is constant

下面讨论式(37)中的系数s对岩石冻胀力及孔隙率的影响，计算结果如图7 所示。由图7 可知：1)在s一定时，随着冻融循环次数增加，岩石冻胀力及孔隙率均增加，但其增加速率逐渐减小，这说明当循环次数增加到一定程度后，岩石冻胀力及孔隙率将逐渐趋于稳定；2)对于统一冻融循环次数，随着s增加，岩石冻胀力及孔隙率均减小，且其减小幅度逐渐变缓。这说明当s增加到一定程度后，岩石冻胀力及孔隙率将逐渐趋于稳定。总之，s对岩石冻胀力及孔隙率的影响均较大，因此，在实际工程中，应通过试验数据对s进行准确拟合，保证计算结果的准确性。

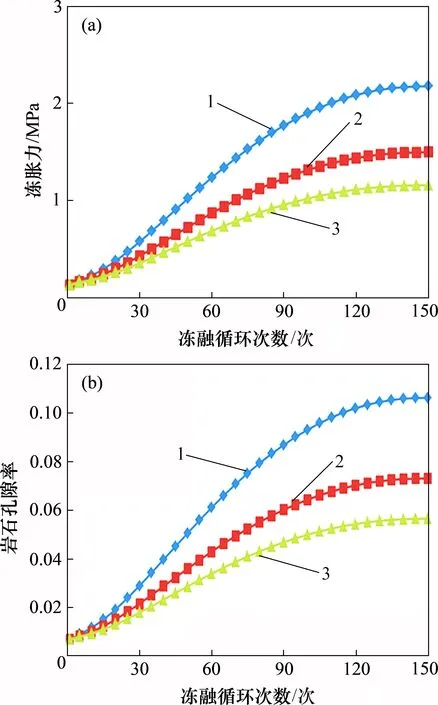
图7 不同冻融循环次数下岩石冻胀力及孔隙率随s的变化规律Fig.7 Variation of rock frost heaving pressure and void ratio with the value of s under different freezing-thawing cycles

5 结论

1)基于Griffith 断裂理论及细观损伤理论建立了岩石弹性模量随冻融循环次数的变化规律，随着冻融循环次数增加，岩石弹性模量逐渐降低，但其降低速率逐渐变小。

2)考虑冻融循环对岩石弹性模量、孔隙率及冻胀率的影响，提出了考虑冻融循环下岩石损伤的圆形隧道围岩冻胀力的损伤力学解答式。

3)随着冻融循环次数增加，围岩冻胀力逐渐增加，并趋于某一定值。岩石冻胀力主要是由岩石孔隙中水的冻结膨胀所致，要减少围岩的冻胀破坏应主要采用截排水措施以控制水的渗入。