基于ANSYS的边坡稳定性关键参数分析

李青山

（新疆水利水电勘测设计研究院,新疆 昌吉 831100）

0 前言

边坡工程在铁路、公路、水利等工程建设中运用非常广泛，同时，边坡的稳定性也影响着上述工程的施工安全、运营安全以及建设成本。因此，开展工程边坡稳定性分析，非常重要。

岩土体参数的确定是边坡支护设计的首要工作，对边坡稳定性影响因素进行敏感性分析，国内外许多学者已做了大量的工作，并取得了一定的成果[1～4]。影响边坡稳定性的因素归结起来分为三类：边坡岩土体力学特性参数、边坡几何尺寸参数、边坡所受外部荷载。经过大量的工程实际以及室内试验分析发现，边坡岩土体力学特性参数中的黏聚力和内摩擦角是较为关键的因素。已有研究表明[5～9]，岩土体变形剪切过程中，初始加载时主要是黏聚力抵抗施加的应力，当荷载达到临塑荷载，黏聚力达到峰值并开始降低，而土粒之间的摩擦力开始发挥作用，并逐步增大至最大内摩擦角值，岩土体剪切破坏过程中黏聚力和内摩擦角的衰减程度并不一致。因此实际工程设计中采取的粘聚力与内摩擦角同比例折减计算的准确性值得深入思考。

本文基于ANSYS有限元分析，结合ANSYS边坡工程经典算例，首先选取初始折减系数（安全系数），将岩土体的粘聚力和内摩擦角进行三类折减：①粘聚力不变，内摩擦角折减；②内摩擦角不变，粘聚力折减；③粘聚力、内摩擦角同时折减。将折减后的参数作为输入，进行有限元计算，并采用程序是否收敛作为边坡岩土体稳定判断依据，若程序收敛，则边坡岩土体仍处于稳定状态，当程序不收敛，则说明边坡已经破坏。模拟结果为工程中通过强度折减进行边坡支护设计、验算、施工等提供理论与应用参考。

1 有限元分析模型

1.1 基本假定和模型

（1）实际工程中，边坡岩土体为纵向很长的实体，因此，参考弹塑性力学中的理论，把边坡岩土体稳定性分析这一空间问题简化为近似的平面问题（见图1）。假定边坡所承受的外力不随Z轴变化，位移和应变都发生在自身平面之内。

图1 边坡几何尺寸图

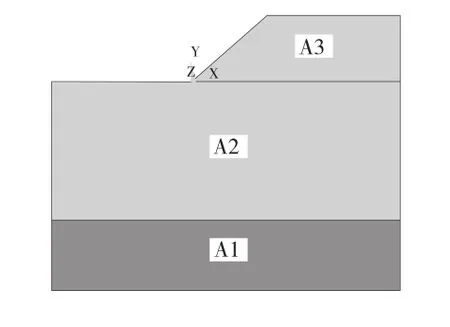
图2 计算模型纵剖面示意图

（2）考虑模型四周与相邻土体的相互约束，边界条件为：对模型左右两边界节点加水平约束，对模型下边界节点加水平和竖向约束，上边界不加约束。

（3）A1（滑坡体）、A2（滑床）采用Drucker-Prager弹塑性模型，A3（基床）采用线弹性模型。

（4）不考虑岩土体的抗拉强度。

1.2 模型网格单元的划分

图3 边坡模型单元网格

1.3 模型岩土体参数

有限元分析时，A3 区域的基床岩土体可看作线弹性材料，只需考虑弹性模量E、泊松比µ和重度γ等3 个参数。在折减时不考虑边坡岩土体弹性模量E、泊松比µ和重度γ的变化，即控制这三个参数为不变量。具体参数见表1。

表1 边坡模型岩土体参数

进行折减时，只对A3 区域的岩土体进行。强度折减系数 分 别 为：F=1.2、F=1.4、F=1.6、F=1.8、F=2.0、F=2.2、F=2.4、F=2.6、F=2.8、F=3.0。折减后的边坡岩土体具体数值见表2、表3。

表2 A3黏聚力折减后参数

表3 A3内摩擦角φ折减后参数

2 黏聚力折减对边坡稳定性影响分析

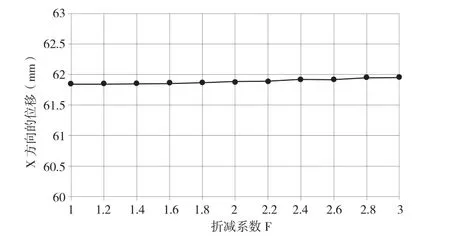
图4 X方向位移随黏聚力折减变化图

图5 黏聚力折减系数F=3.0时边坡模型塑性应变云

由图4 分析可知，X方向的位移随着黏聚力的折减变化极小，几乎可以忽略不计，因此我们可以断定，黏聚力对于岩质边坡的稳定性影响很小。

由图5 可知，当黏聚力折减系数达到3.0 时，边坡依然没有发生塑性变形。

3 内摩擦角折减对边坡稳定性影响分析

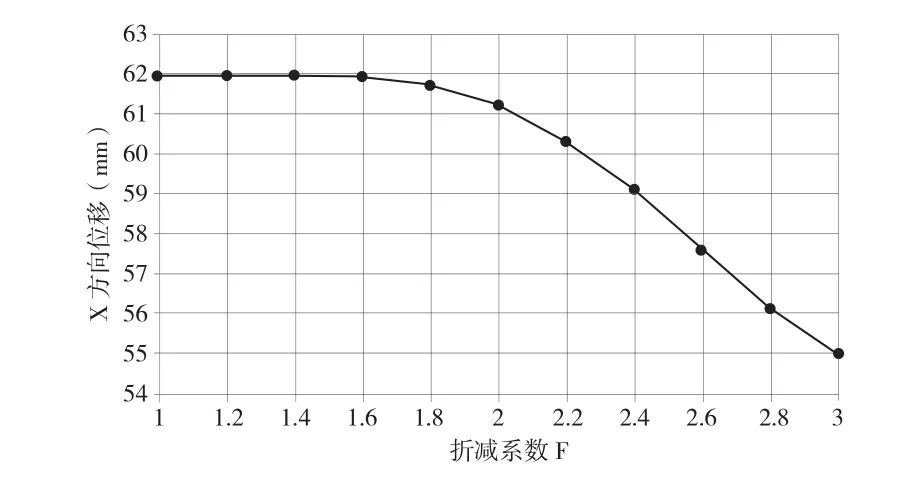
图6 X方向位移随内摩擦角折减变化图

由图6 分析可知，X方向的位移随着内摩擦角的折减开始变化较小，当折减系数达到1.6 以后，X方向的位移增长速率加快，因此我们可以断定，内摩擦角对于岩质边坡的稳定性影响相对黏聚力大。

由图7、图8 对比分析可知，当内摩擦角折减系数达到1.6时，边坡岩土体于坡脚处发生塑性变形，并逐步向上扩展。

由图9 可知，当内摩擦角折减系数达到3.0 时，边坡坡脚较大范围内的岩土体都已经产生塑性应变，其最大值达到2.98 E-4。

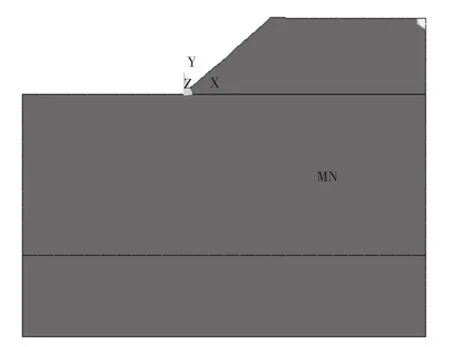
图7 内摩擦角F=1.8时塑性应变云

图8 内摩擦角F=1.8时塑性应变云

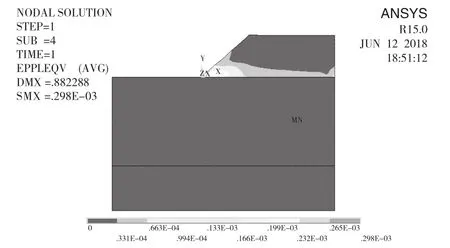
图9 内摩擦角F=3.0时塑性应变云

4 黏聚力、内摩擦角相同系数折减对边坡稳定性影响分析

图10 X方向位移随黏聚力、内摩擦角同比例折减变化图

由图10分析可知，X方向的位移随着内摩擦角的折减开始无变化，当折减系数达到1.4以后，X方向的位移增长速率加快。与单独内摩擦角的X方向位移变化图相对比，我们可以发现同时折减黏聚力与内摩擦角，会稍微加快边坡岩土体的变形。

当折减系数F大于2.2 时，边坡水平方向位移急剧下降，说明边坡已经处于塑性状态，接近于破坏状态。

图11 F=2.4求解迭代收敛过程图

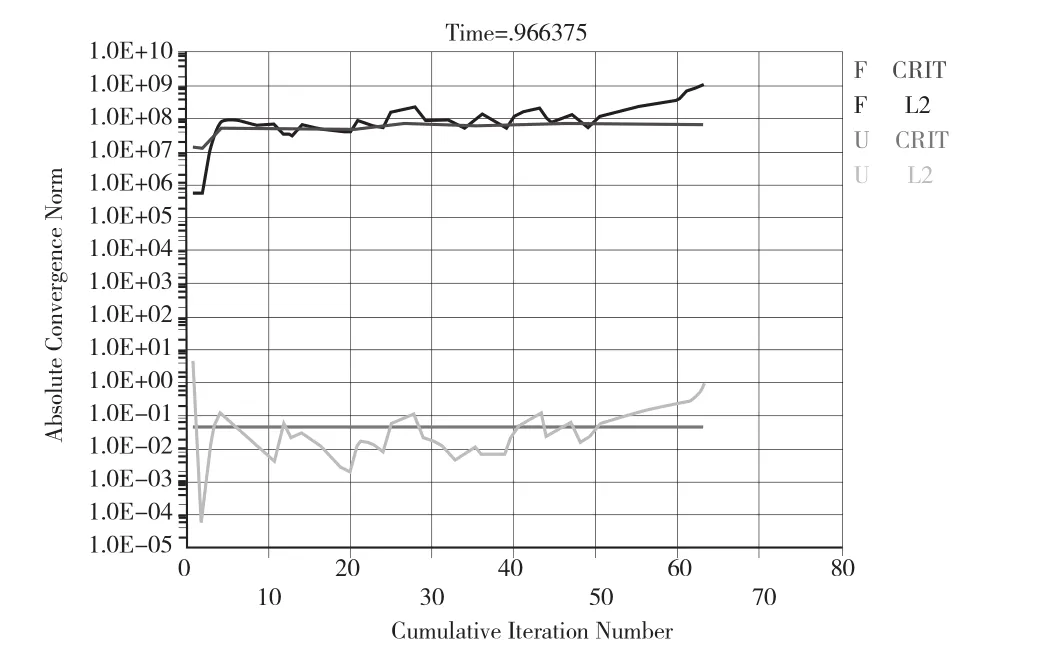
图12 F=2.6求解迭代不收敛过程图

对比分析图11 与图12 可知，当边坡折减系数处于2.4～2.6之间时，边坡失稳。为了较为准确预估边坡的塑性应变，特此生成F=2.4 时的塑性应变云图，见图13。此时，边坡塑性应变大小为1.24 E-3。模型中塑性区扩大，并即将贯穿到坡顶，说明此时边坡已经濒临破坏。

图13 黏聚力、内摩擦角F=2.4时塑性应变云

5 结论

（1）边坡稳定性影响因素众多，黏聚力c与内摩擦角φ的折减系数之间不存在惟一确定的函数关系，且黏聚力的变化对岩质边坡的影响较小，内摩擦角φ对岩质边坡的稳定性影响较大。

（2）通过假定黏聚力c和内摩擦角φ按某一比例进行强度折减的处理方法可以为提高工程技术人员对边坡支护设计的效率，但两种强度指标真实的折减比例却还需进一步的试验论证。

（3）由于内摩擦角φ值对边坡稳定性分析有着较大影响，尽可能准确测量出φ值对边坡稳定性设计与节约成本具有重要意义。