纯弯状态下高硼硅玻璃棒级联断裂的条件研究

王晓萌 倪俊宇 吴旷达 王盛伟 张培伟

（东南大学土木工程学院，江苏 南京211106）

级联断裂这个问题最早可以追溯到理查德·费曼的意大利面试验。在之后的几十年的时间内,许多科学家都对此问题进行了研究但都没有打破规律。

在2005 年，在这个问题被提出来近五十年后，两位法国科学家Basile Audoly 和Se'bastien Neukirch 在Physics Review Letters 上发表了一篇论文。在文章中，两位学者考虑了在面条弯曲初始断裂后的情景[1]。

在他们发表这篇论文前几个月，美国和法国的一个团队就意大利面断裂问题，在Physics Review Letters（PRL）发表了一篇论文。这个小组的视角与他们略有不同，关注的是动态冲击而不是准静态载荷，发现面条也是断裂成几截[2]。

2018 年，PNAS 上发表了一篇名为《Controlling fracture cascades through twisting and quenching》的文章，文章中通过将意大利面进行扭转后再对其施加弯矩直至断裂，此时，面断成了两截，打破了费曼的猜想[3]。

在国内也有相似的研究。其中相关度较高的是湖南大学李凤云对于脆性梁的弯曲波传播问题的研究[4]。

级联断裂是一种灾难性的失效形式，目前建筑，桥梁，机械结构中为了避免此类事故的发生，往往是通过采用性能更好的材料，更夯实的结构形式，冗余度更高的结构设计段[5]，人们至今对级联断裂的机理仍然缺乏完整的理解，也缺乏更经济高效的解决方手段。本文以高硼硅玻璃棒为例，建立了长细杆件级联断裂的理论模型，利用应力波理论分析了长细杆件发生级联断裂的机理。

1 试验概况

1.1 试件及其物理性质

试验采用高硼硅玻璃棒作为试件，高硼硅玻璃棒的各项性质比较均匀，且易于发生脆性破坏，是理想的作为试件的材料。高硼硅玻璃棒的物理参数参见表1。

表1 高硼硅玻璃棒各项参数

1.2 纯弯曲试验方法

采用万能材料试验机进行四点弯加载，恒位移控制加载速率，加载速率为0.5mm/min，计算机自动采集数据。加载至玻璃棒发生断裂，停止加载。

试验采用二分法确定纯弯曲段的长度，先取150mm 为纯弯曲段的初始长度，然后取另一使高硼硅玻璃棒发生不同断裂状态（分为是否发生级联断裂良种化状态）的纯弯曲段长度，然后逐渐向这两个值得中间逼近，直至区间长度小于直径。

2 试验结果与分析

2.1 纯弯曲试验现象

纯弯曲试验过程中，随着荷载的增加，高硼硅玻璃棒弯曲程度增大但不明显，无明显裂痕，荷载增加到一定值，高硼硅玻璃棒突然断裂。断裂的位置大多在高硼硅玻璃棒的三等分点的中间区段，以这种形式断裂的高硼硅玻璃棒断裂后的碎片较多且较小，部分高硼硅玻璃棒在压头位置断裂，且多断裂为两段。

2.2 纯弯曲试验结果

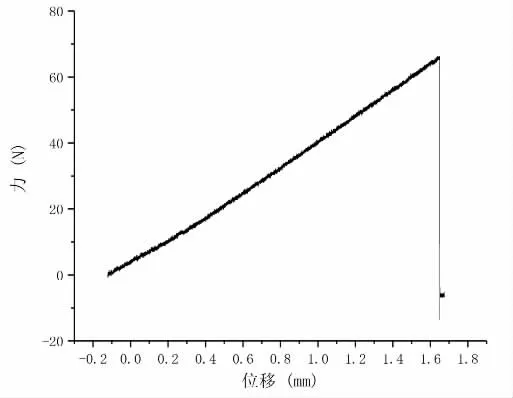
图1 纯弯状态下高硼硅玻璃棒P-δ 曲线

由高硼硅玻璃棒的P-δ 曲线可见：高硼硅玻璃棒的P-δ曲线大致呈现一条直线，高硼硅玻璃棒在纯弯状态下始终处于弹性状态。

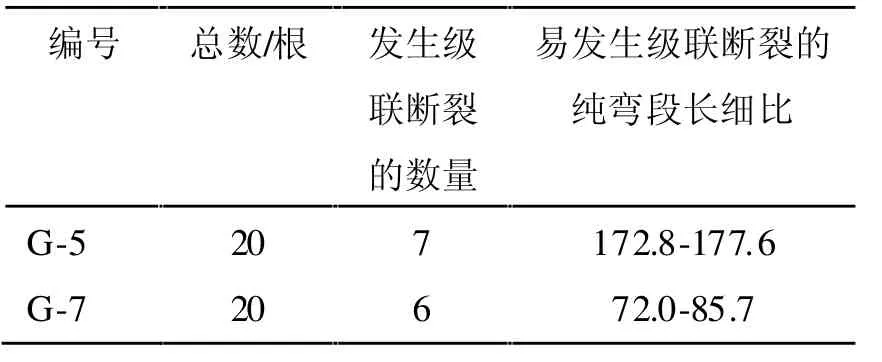
表2 高硼硅玻璃棒数据测量表

表2 是高硼硅玻璃棒发生级联断裂时的统计结果。高硼硅玻璃棒发生断裂时的中点挠度，中点曲率和最大应力的各项数值（这里只列举发生级联断裂的高硼硅玻璃棒）参见表3。

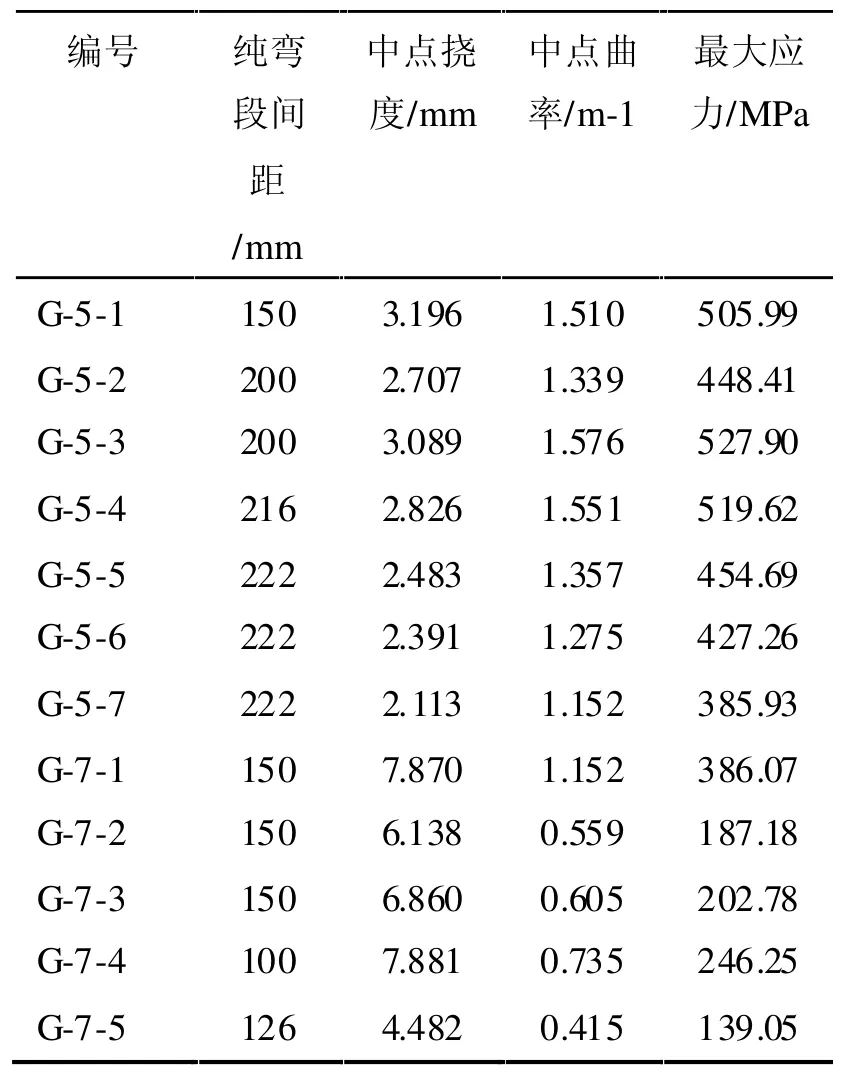
表3 高硼硅玻璃棒发生级联断裂时的各项数值

2.3 应力波理论分析

根据纯弯曲梁的弹性力学精确解，其横截面保持为平面，两端简支的玻璃棒纯弯曲问题可简化为一维问题[6]。在一维杆的纵向运动中，其连续性方程（相容方程）为：

式中：v 为杆中质点的速度，x 为用Lagrange 方法描述的物质坐标，ε 为应变。

一维杆纵向运动的动力学方程为：

式中：ρ 为杆的密度，为不随时间与空间变化的常量，σ 为应力。

为了简化模型，玻璃棒材料的本构关系[7]

采用：

式中：E 为玻璃棒的弹性模量，为不随空间与时间变化的常量。

引入：

显然，C 也是一个不随时间与空间变化的常量。

将上式（4）与本构关系式（3）代入动力学方程（2）得到：

采用特征线法求解得特征线上相容关系：

或

可见C 表示物质波面传播的速度。上式（7）确定了应力σ与质点速度v 之间的关系，称ρC 为波阻抗或声阻抗。

如果u 的一阶导数间断，也即质点速度v 和应变ε 在波阵面上有突跃，则称为一阶奇异面或强间断，这类应力波也称为冲击波。

应力波根据传播方向分为左行和右行。对于右行冲击波，根据质量守恒条件，波阵面上的运动学相容条件为：

根据动量定理，波阵面上的动力学相容条件为：

对于左行波，其波阵面相容方程将-C 替换上式中的C 即可。

下面考虑应力波在自由边界处上的反射。对于被施加了轴向冲击的一维杆件，假设其左右两端初始状态分别为v1，ε1，σ1与v2，ε2，σ2（图2a），分别对应图2(f)中的1、2 两点。之后应力波分别以波速C0 向中间传播，当两波相遇时，应力波发生反射，向两端传播。相遇点处速度、应力发生突变，设为v3、σ3。

根据波阵面上的相容条件（式9）

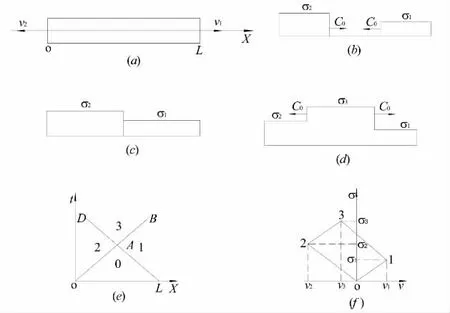
图2 迎面传播的两冲击波的相互作用

可解得σ3、v3，对应于图2（f）中的状态3。也可以根据叠加定理求得。

若在自由端发生反射，则

有v2=v1，v3=2v1。

另外，应力波在不同介质中发生反射与透射时，入射波扰动ΔσⅠ传递到界面上时，反射波扰动

式中：F 为反射系数，满足

式中：n 为两介质的声阻抗之比。

纯弯曲下的玻璃棒发生断裂时，断面的应力突然释放，相当于在两端施加了一个冲击荷载，其在断面造成的初始应力与静态弯曲荷载下的应力的叠加为效果为0，即边界成为自由端。随后该冲击荷载造成的应力波分别从两端向中间传播，相遇后发生反射，在自由端面再次反射后成为加载波，与静荷载下的弯曲应力叠加，造成二次断裂或者多次断裂。且静载下的应力越大，一次断裂后，更容易发生二次或多次断裂，即级联断裂。

此外，与层裂或崩落现象类似，断裂的玻璃棒碎片会带着传递的脉冲的全部动量飞出，因此碎片具有初始速度。且因为裂缝间存在一定间距，即碎片具有一定长度，其两端的运动状态并不一致，速度不相等，因此在飞出的过程中还会产生角速度。

从直接的实验现象看，玻璃棒因级联断裂飞出的碎片的确具有初始速度，与应力波理论相符。

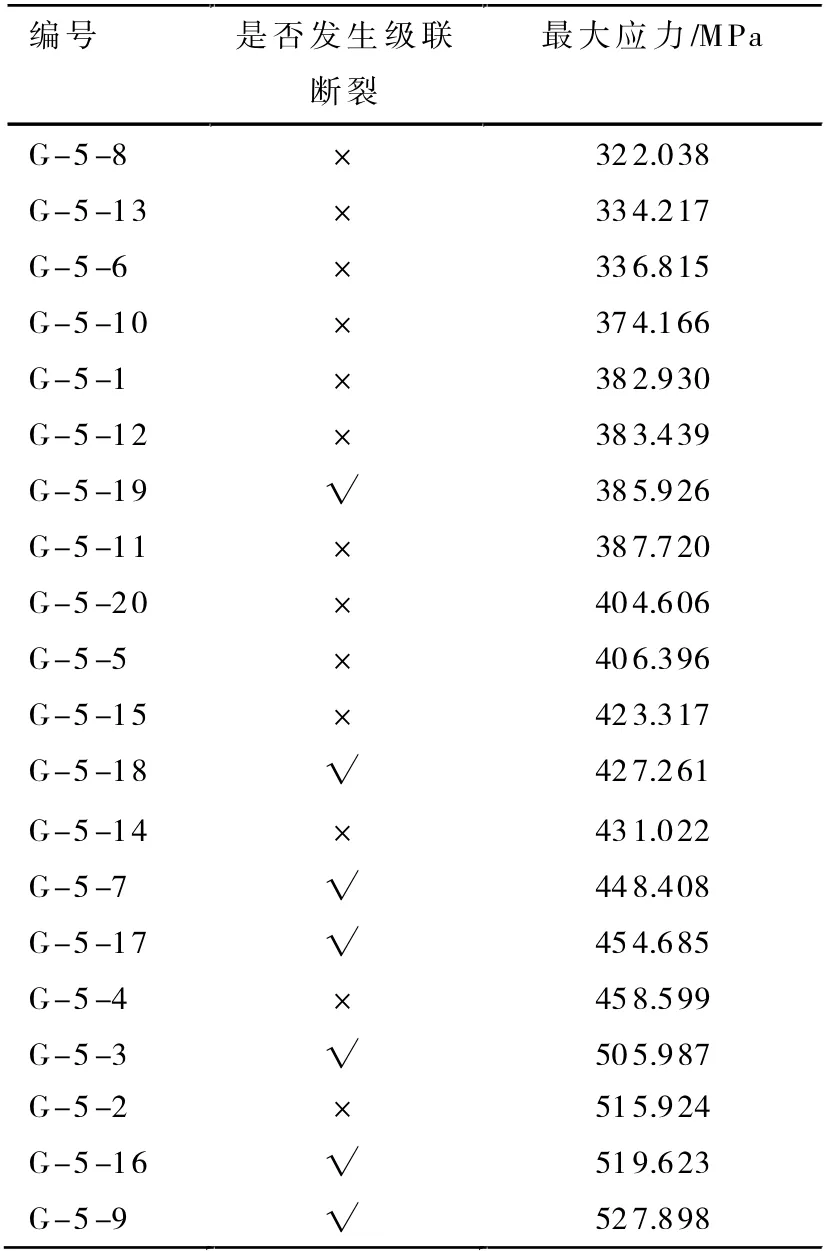
表4 直径5mm 高硼硅玻璃棒最大应力顺序排序

表5 直径7mm 高硼硅玻璃棒最大应力顺序排序

从表4、表5 可以看出，如果玻璃棒有瑕疵，则较早断裂，不会发生级联断裂；如果玻璃棒品质越好，则其断裂时的挠度越大、最大应力也越大，也更容易发生级联断裂，与应力波理论相符。

3 结论

本文通过对不同尺寸的高硼硅玻璃棒进行纯弯曲试验，并用应力波的相关理论对试验的数据和现象进行分析，得到如下结论：

3.1 在纯弯曲状态下，高硼硅玻璃棒发生级联断裂的位置在纯弯曲段的三等分点的中间区段。高硼硅玻璃棒发生级联断裂时需其纯弯曲段曲率很大。

3.2 对于纯弯曲状态下的高硼硅玻璃棒，其中点应力达到一定值后，高硼硅玻璃棒突然断裂，断口处的边界条件突然变为自由边界，应力突变为0，相当于在两端突然施加一个冲击，应力σ 和速度v 突变，产生的冲击应力波，并向另一端传播，导致高硼硅玻璃棒发生二次断裂，甚至多次断裂。

3.3 猜想：杆件断裂，由杆件断口处产生冲击应力波，应力波在杆件中传播，反弹，叠加，达到杆件的承载极限，发生再一次的断裂，断裂一直持续直至能量不足以引发断裂。