双二次交换作用和各向异性对反铁磁体相变温度的影响*
2020-06-04文林胡爱元
文林 胡爱元
(重庆师范大学物理与电子工程学院, 重庆 401331)(2020年1月12日收到; 2020年3月24日收到修改稿)
本文基于双时格林函数方法, 通过对不同格点和同格点的高阶格林函数分别采用Tyablikov 和Callen 退耦近似, 系统研究了双二次型交换作用和各向异性对简单立方晶格反铁磁模型相变的影响. 得到了相变温度的解析表达式, 发现相变温度随着各向异性的增强而升高, 但随着双二次型相互作用的增强而下降.
1 引 言
双二次型(biquadratic)交换相互作用可以通过对双线性(bilinear)相互作用进行高阶展开来得到, 其强度比双线性相互作用弱[1−3]. 实验上可以通过微波共振技术手段观察到[4], 对材料的性质有着重要的影响. 例如: 一维材料LiVGe2O6的磁化率[5,6]以及超导材料Ca(Ba)Fe2As2[7,8,9], FeSe[10,11]的磁激发需要引入双二次相互作用才能合理解释.化合物GdMg 中的双二次型相互作用导致系统磁化强度不是按布洛赫定理的T3/2减小(T为温度),而是T2减小[12,13]. 最近, Yu 和Nevidomskyy[14]在研究超导材料的配对状态时发现: 适度的双二次相互作用不仅会导致掺杂的配对对称性、配对强度和能隙各向异性发生显著变化, 而且是调节掺杂下各种超导态稳定性的关键因素.
在以往的研究中, 研究者采用不同的方法探讨了双二次型交换相互作用对铁磁模型的磁化强度、居里温度、磁化率的影响, 如: 平均场理论[15]、自旋波理论[16]、高温展开法[17]、格林函数方法[18,19]等.相比铁磁模型, 研究双二次型交换相互作用对反铁磁模型相变温度影响的工作较少[19,20]. 除此以外,在实际材料中存在各向异性, 它在磁性系统相变中也扮演着至关重要的角色. 因此, 本文将采用双时格林函数方法研究双二次型相互作用和各向异性共同对反铁磁模型相变的影响. 结果显示: 交换各向异性在0 到1 取值时, 反铁磁模型的相变温度总是随着双二次型交换作用的增强而下降. 而铁磁模型却存在一个临界的各向异性, 其相变温度的大小不受双二次型相互作用的影响, 大于临界各向异性, 相变温度随着双二次型相互作用的增强而升高, 反之下降[19].
2 理论模型
理论模型是一个三维简单立方晶格, 它由两个子晶格构成, 不同子晶格自旋方向相反, 每个子晶格中磁性离子的自旋量子数为1, 即S=1 . 因此,该晶格的磁结构是一个Nèel 型结构. 在这里, 采用字母a和b来分别标识这两个子晶格, 其相应子晶格的自旋算符分别用和来标识,α=x,y,z表示自旋算符的三个分量. 因此, 一个包含了双二次型相互作用和各向异性的简单立方晶格反铁磁体模型的哈密顿量可以表示为

这里J1和J2分别描述的是最近邻自旋间双线性和双二次型交换相互作用.表示对最近邻格点求和.η是交换各向异性参数, 其取值范围为0η1 . 当η=0时, 模型退化为Ising 模型. 显然, 越小的η对应着越强的交换各向异性.D描述的是两个子晶格的单粒子各向异性. 选z轴为量子化轴, 取子格a的自旋方向为正, 则子晶格磁化强度定义为自旋算符的统计平均, 即:本文不作特别说明, 均取J1=1 , 探讨其它参数改变时对系统性质的影响.
接下来, 采用双时格林函数方法推导模型子晶格磁化强度的解析表达式, 基于这个目的, 构建了如下的格林函数:
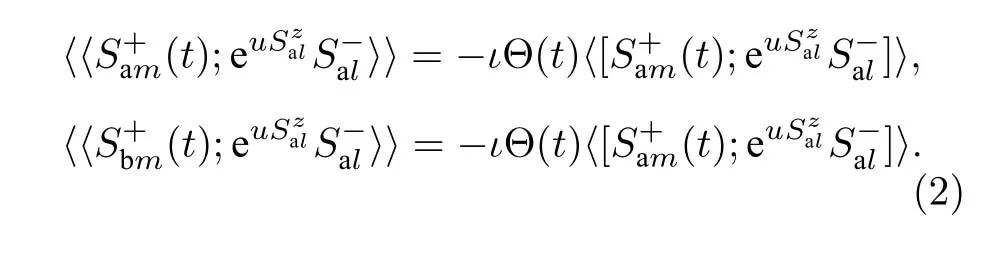
这里

κB是玻尔兹曼常数. 为了方便, 令κB=1 , 则系统所有的量, 包括交换常数、磁化强度、温度皆是一个无量纲的量.u是Callen 参数[21], 在求解格林函数的运动方程中, 其值会取零, 以此得到子晶格磁化强度的自洽方程. Θ (t) 是阶跃函数. 根据双时格林函数的标准步骤[21], (2)式的两个格林函数的运动方程可以写为


对同格点的高阶格林函数, 采用Callen 退耦近似[23], 即:

这里,

注意: 对于同格点退耦, 两个子晶格C1的表达式不一样, 但它们的大小相差一个负号, 即
对于类似(3)式中的高阶格林函数a,
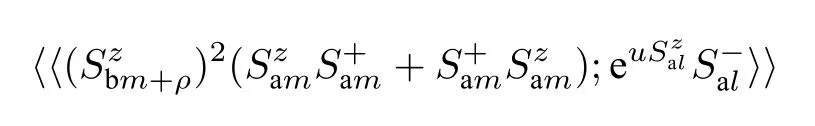
首先近似为

然后再采用Callen 退耦近似.
采用上面的退耦近似后, 对格林函数进行空间和时间傅里叶变换, 得到两组代数方程, 易求得傅里叶变换后的格林函数gk(ω) 和fk(ω) , 即:

这里,

其中γk是结构因子, 对于简单立方晶格,γk=是最近邻格点数.
令
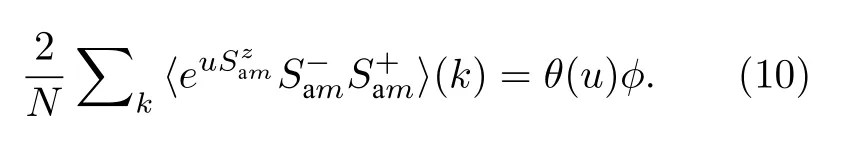
这里N是晶格格点数, 求和遍及第一布里渊区. 通过谱定理[21], 可以求得等时关联函数对则关联函数可以表示为

将(11)式代入(10)式得

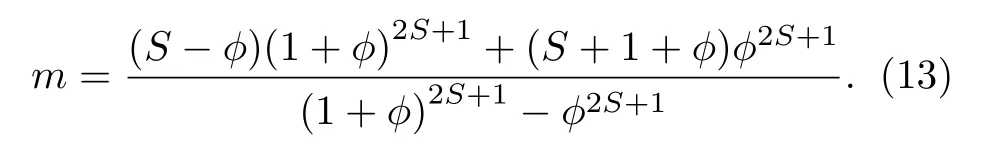
当温度趋于相变点时,m是一个小量, 则(12)式的自旋波谱也是一个小量. 对(12)式右边进行泰勒展开得

在这种情况下, (13)式可近似为
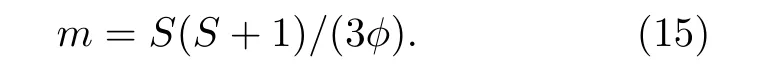
联合(14)和(15)式, 可得系统相变温度的解析表达式, 即:

3 结果与讨论
由于晶格格点数N很大, 因此(16)式对k在第一布里渊区的求和可以变换为对k的连续积分, 即:
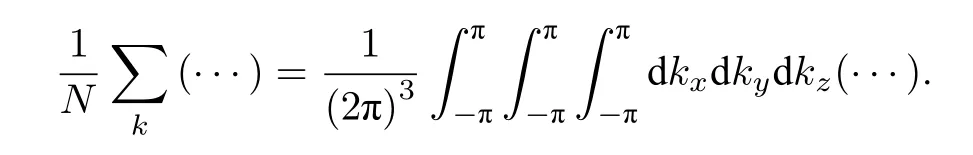
接下来, 通过对(16)式积分来探讨双二次型交换作用和各向异性对自旋量子数S=1 的简单立方晶格反铁磁模型相图的影响.
首先探讨在各向异性确定的条件下, 双二次型交换作用对系统相变温度的影响. 图1 描述了单粒子各向异性D取0, 1时, 不同η(交换各向异性)值下的相变温度TN与双二次型交换作用J2之间的变化关系. 从总体看, 无论各向异性取何值,TN值随着J2增大而变小. 对于确定的J2值, 系统各向异性越强(即η值越小、D值越大),TN值越大. 当η=0时,TN与J2之间呈线性关系, 且系统各向异性越强, 它们之间线性关系越明显, 见图1(b).当η̸=0时, 在J2的临界值附近(见图1(b)), 相变温度曲线下降迅速.
对比铁磁模型的结果发现: 它们之间的差异显著.对于铁磁模型[19], 当D值确定时, 存在一个ηc值,此时系统 TN值不受J2影响, 即在这种情况下,TN值随着J2的增大保持不变. 当η<ηc时,TN随着J2的增大而升高; 当η>ηc,TN值随着J2增大而变小. 而反铁磁模型的TN值在 0η1 的范围内总是随着J2的增大而减小. 同时, 不论各向异性取何值, 铁磁模型的TN与J2之间始终成线性关系[19].而反铁磁模型仅在η=0时, 这种线性关系才存在.
下面讨论其它理论在J2=0时的相变温度. 当D=0.01,η=0时, 相变温度值为4.005, 其结果比Linked-cluster series expansion 方法的3.19[24]和Ratio method 的3.19[25]要大, 比平均场得到的4.007 略小[24]. 这是因为, 对于Ising 模型, 基于格林函数的Tyablikov 近似与平均场近似是等价的,但由于本文的单粒子各向异性采用了更精确的Callen 近似, 所以本文的相变温度值要稍小于平均场的结果. 当D=0时, 本文得到的相变温度4.0 与平均场近似的结果是相等的. 对于D=0 ,η=1, 本文得到的相变温度值为2.64, 其结果接 近Linked cluster series expansion (2.74)[24],Ratio method (2.72)[25]和 High-temperature series expansion method (2.73)[26].

图1 当单粒子各向异性参数D 取0 和1时, 交换各向异性参数 η 为0, 0.5, 0.9, 1 下相变温度 T N与双二次型交换作用 J2 之间的关系曲线Fig. 1. Nèel temperature as a function of biquadratic exchange for the exchange anisotropic parameter η =0,0.5,0.9,1 when the single-ion anisotropic parameter D =0 and 1.
从图1 可以发现, 对于确定的各向异性, 存在一个临界的值. 类似地, 对于确定的J2, 也存在一个临界的各向异性(本文没有给出TN与η的相图, 原因是其结果与图1 的结果重复). 这意味着对于一个确定D, 存在一组η和J2数据, 这组数据得到的曲线是系统从有序向无序转变的临界曲线.图2 给出了当D取0, 1时, 系统在参数η和J2空间中的相图, 它清晰地给出了不同η和J2值时, 系统有序和无序转变的边界. 对于确定的η和J2, 系统有序区域会随着单粒子各向异性增强而变大. 这是因为各向异性越强, 其抑制系统扰动能力越强,导致了越大的相变温度(见图1), 这意味着系统有序区域变大. 正是由于这个原因, 对于确定的单粒子各向异性, 有序区域会随着η的变小(越小的η对应着越强的各向异性)而增大. 而系统的相变温度随着J2增大而下降, 这表明J2增大使得系统有序区域变小. 这表明对于确定的单粒子各向异性, 系统有序区域的大小实际上是η与J2之间相互竞争的结果, 即: 在J2值比较小时, 系统各向异性η占据主导作用, 于是图2 中的有序区域随着η的变小而增大. 当它们之间竞争达到最大时, 系统有序区域大小也随之达到最大. 之后随着J2的增大, 系统有序区域变小, 此时J2占据主导作用. 于是系统各向异性在达到最强的过程中(即η→0 ), 有序区域一 直在变小.

图2 当 D =0,1时, 系统在参数 η 和 J2 空间中的相图Fig. 2. Phase diagram of the D =0,1 in the η and J2 parameter space.
4 结 论
本文采用双时格林函数方法, 对不同格点的高阶格林函数采用Tyablikov 退耦近似, 对于同格点的高阶格林函数采用Callen 退耦近似, 推导得到了子晶格磁化强度和相变温度的解析表达式. 通过数值计算, 详细探讨了双二次型交换作用和各向异性对系统相图的影响. 结果表明: 相变温度随着各向异性的增强而升高, 但随着双二次型相互作用的增强而下降. 当J2=0时, 本文的相变温度值与其它理论结果一致.
感谢清华大学物理系王怀玉教授的讨论.
