Re 对Ni3Al 微观结构及力学性质影响的第一原理研究*
2020-06-04胡雪兰卢睿智王智隆王亚如
胡雪兰 卢睿智 王智隆 王亚如
(中国民航大学中欧航空工程师学院, 天津 300300)(2020年1月14日收到; 2020年3月17日收到修改稿)
应用基于密度泛函理论和广义梯度近似的第一原理方法, 探究了Re 元素掺杂镍铝合金中 γ′ 相Ni3Al 之后微观结构和力学性质的变化. 结果表明, 在大部分化学计量比范围内, Re 原子在Ni3Al 中易于替代Al 位.Re 的掺杂引起Ni3Al 晶格常数小幅度地增大, 且不会引起严重的晶格畸变. 通过差分电荷密度及态密度分析得到Re 原子与近邻原子产生轨道相互作用, 尤其是与Ni 原子作用较强, 并使周围Ni-Al 键键能降低. 通过计算弹性模量, 应用经验判据得到掺杂后Ni3Al 的刚性、硬度增强. 随着Re 掺杂浓度的增加, Ni3Al 晶格常数、刚性和硬度随之增大. 为了对第一性原理所得结果进行温度修正, 进一步结合声子谱计算考察了温度对力学性质的影响. Re 的掺杂使得Ni3Al 晶胞的熵略微增加, 自由能略微降低, 并且大幅度地增加Ni3Al 在高温下的体弹性模量, 同时降低Ni3Al 在高温下的热膨胀系数.
1 引 言
当今航空航天的发展亟需具有高熔点、高导热性、高弹性模量等优异性能的材料[1,2]. 高温合金中的Ni3Al 合金具有许多优良的性能, 例如: 高熔点、抗高温氧化、耐腐蚀、具有较大的高温强度和蠕变强度等[3−5], 这些特性使得它能够广泛地在军用和民用工业中应用.
尽管Ni3Al 合金有着许多优良的性能, 但是其韧性较差, 屈服强度较低, 并且为了满足新一代航空涡轮发动机更高的要求, 人们发现在Ni3Al 合金中可添加一些合金元素进一步对其力学性能进行改善和提高. 目前的研究表明, Fe 对Ni3Al 合金的延展性和机械性能具有增强的作用[6]. Cr 元素的掺杂能够增加Ni3Al 的体积模量[7]. Mo, Ta, W,Ti, Nb 和Ru 元素的掺杂增加单晶Ni3Al 的杨氏模量和剪切模量[8]. Be 元素能使Ni3Al 塑性提高,添加1%(原子)Be, 可使延伸率达到5%[9]. Mn 元素可以改善Ni3Al 合金的室温拉伸性能, 随着Mn 含量的增多, 合金屈服强度及延伸率均相应提高[10]. Zr 和Hf 能够提高Ni3Al 合金的流变应力以及 [ 101](111) 滑移系的临界分切应力[11]. 在这些合金元素中, Re 的地位非常重要. Re 元素能够使Ni3Al 性质表现出良好的改进, 高温蠕变强度、抗氧化性和热疲劳阻抗等都能得到巨大的改善[12,13].前三代镍基单晶高温合金发展的一个显著特点是Re 的浓度不断增加, 这已证明Re 是显著提高镍基合金机械性能的关键因素[14]. 但是有关含Re 的Ni3Al 基高温合金拉伸性能及相互作用的微观机理方面的研究比较少. 因此本文通过第一性原理计算Re 对Ni3Al 差分电荷密度、态密度及弹性模量的影响, 探究Re 与Ni3Al 中其他原子相互作用的微观机理. 另外, 为了对第一原理计算结果进行温度影响的修正, 论文结合声子谱计算分析了Re 对Ni3Al 热力学性质的影响, 其中热膨胀系数和体弹性模量的计算采用准谐波近似.
2 计算模型与方法
计算应用基于密度泛函理论和广义梯度近似的第一原理方法, 采用的计算软件为VASP, 其中有关热力学性质的计算结合了声子谱计算和准谐波近似方法(QHA). 离子和电子间的相互作用采用超软赝势. 晶体波函数用平面波基展开, 平面波动能的截止能为500 eV. 计算晶胞结构、电子结构、弹性模量和热力学性质的过程中均采用3 × 3 ×3超晶胞, 对布里渊区的积分采用3 × 3 × 3 的Monkhorst-Pack 均匀k点网格. 计算所得晶格常数与实验值3.570 Å非常符合[11], 结构弛豫计算的收敛判据为原子间作用力小于10–3eV/Å.
3 结果分析
3.1 Re 在Ni3Al 中的溶解能
为了研究Re 对Ni3Al 微观结构及力学性质的影响, 需确定Re 在Ni3Al 中的最优位置. Re 和Ni 的 原子半径均为135 pm, Al 的 原子半径为125 pm, 考虑到Re 的原子半径与Ni, Al 原子的半径相近, 以及Ni3Al 的L12面心立方结构, 因此在计算时选择Ni 位、Al 位和在L12结构中空间较大的八面体间隙位为Re 可能的掺杂位置, 如图1 所示.

图1 L12 Ni3Al 晶胞及Re 可能的掺杂位置示意图 (a) Ni3Al晶胞示意图; (b) Al 替代位; (c) Ni 替代位; (d) 八面体间隙位置Fig. 1. The crystal structure of L12 Ni3Al and different sites for Re in Ni3Al: (a) The crystal structure of Ni3Al; (b) Al substitution site; (c) Ni substitution site; (d) octahedral interstitial site.
Re 的能量最稳定位置需通过计算Re 在Ni3Al 中三种不同位置的溶解能来判断, 替位溶解能和间隙溶解能的公式如下[15,16]:


其中分别代表单个Ni 原子、单个Al原子和纯Ni3Al的化学势, ∆H代表Ni3Al 的生成焓. 设结合(5)式和( 6)式得出:
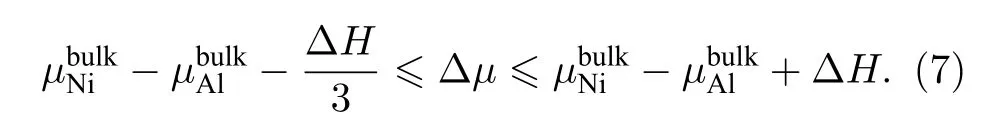
Re 原子在Ni3Al 中替代Ni 位、替代Al 位和占据八面体间隙的情况下, Re 的溶解能随Ni 和Al 原子化学势之差 ∆µ的变化如图2 所示.
由图2 可知, 在整个化学计量比的范围内,Re 位于八面体间隙的溶解能大于Re 位于替代位的溶解能. 在大部分的化学计量比范围内, Re 替代Al 位的溶解能小于Re 替代Ni 位的溶解能, 且∆µ在[–1 eV, –0.09 eV]区间内, 替代Al 位的溶解能为负值, 说明Re 掺杂较容易实现. 因此, 在Ni3Al 中Re 易于占据Al 位, 此结论与已报道的一些计算和实验结果相符[17−21]. 在后续研究Re 对Ni3Al 微观结构和力学性质影响的过程中, 选取Al 位为Re 原子的掺杂位置.

图2 Re 替代Ni 位、替代Al 位和占据八面体间隙的情况下溶解能随Ni/Al 的浓度变化图Fig. 2. The variation of dissolution energy with Ni/Al concentration when Re is substituted for Ni or Al site or occupied octahedral interstice.
3.2 Re 对Ni3Al 微观结构的影响
3.2.1 Re 对Ni3Al 晶胞结构的影响
在晶胞结构方面, 研究了Re 对Ni3Al 晶格常数和化学键的影响. 当掺杂浓度为0.93%, 即1个Re 原子掺杂Ni3Al 超晶胞(Ni3Al-1Re), 晶格常数为3.581 Å, 与纯Ni3Al 晶格常数的模拟值3.579 Å相比变化不大. 当掺杂浓度为1.85%, 即2个Re 原子掺杂Ni3Al 超晶胞(Ni3Al-2Re), 晶格常数为3.584 Å, 与纯Ni3Al 相比仍然变化不大, 说明Re 原子的掺杂对于Ni3Al 没有引起严重的晶格畸变. 随着Re 掺杂浓度的增加, Ni3Al 的晶格常数缓慢增大.
由图3(a)和图3(b)分析可知, Re 掺杂Ni3Al 后, 主要与近邻的Ni 原子成键. Re—Ni 键键长(2.516, 2.519, 2.516 Å)小于掺杂前Al—Ni键键长(2.527, 2.527, 2.531 Å). Re 掺杂前后, 掺杂点位与附近Ni 原子所成化学键键角均约为 60◦.关于Re 对附近Ni—Ni 键和Ni—Al 键的影响, 如图3(c)和图3(d)所示.
Re 掺杂前, 被替代的Al 原子附近的Ni-Ni 键键长分别为2.531, 2.527, 2.531 和2.527 Å, 附近的Ni—Al 键键长均为2.531 Å. Re 掺杂后, Re 原子附近的Ni—Ni 键键长分别为2.515, 2.515,2.534 和2.534 Å, 附近的Ni—Al 键键长分别为2.547, 2.559 和2.547 Å. 说明Re 的加入使得附近Ni—Al键键长增大, 键能降低, 使得附近的部分Ni—Ni键键长减小, 键能增强, 部分Ni—Ni 键键长增大,键能降低.

图3 Re 替代前后掺杂位置近邻的化学键 (a) Re 替代前Al原子与近邻Ni 所成的化学键; (b) Re替代后与近邻Ni所成的化学键; (c) Re替代前掺杂点位附近Ni—Ni键和Ni —Al键的情况; (d) Re替代后掺杂点位附近Ni—Ni 键和Ni—Al 键的情况Fig. 3. The nearby bonds around doping position before or after Re substitutes: (a) The bonds formed between Al and neighboring Ni before Re substitutes; (b) the bonds formed between Re and neighboring Ni after Re substitutes; (c) the nearby Ni—Ni bonds and Ni—Al bonds around doping position before Re substitutes; (d) the nearby Ni—Ni bonds and Ni—Al bonds around doping position after Re substitutes.
3.2.2 Re 对Ni3Al 电荷密度的影响
为了进一步研究Re 对Ni3Al 微观结构的影响, 对Re 掺杂后附近的差分电荷密度进行分析.差分电荷密度即:

其中 ∆ρ代表差分电荷密度,

和ρRe分别代表掺杂Re 的Ni3Al 的电荷密度、Ni3Al(替代位为空位)的电荷密度和Re 原子的电荷密度. 该差值体现了在Re 掺杂之后体系中新产生的电荷密度分布和电荷转移, 此分布可以分析出Re 原子对附近原子电荷密度的影响.
在图4 中, 黄色区域代表电荷数增加, 蓝色区域代表电荷数减少, 差分电荷密度呈对称分布. 从图4 可以观察到, 电荷主要汇聚在Re 原子与近邻Ni 原子的连线区域, 说明Re 的掺杂增强了与Ni 原子的相互作用, Re 与Ni 原子之间的成键作用较强. 从近邻Ni 原子的角度分析, Ni 在向着Re 原子的方向上得电荷, 在背着Re 原子的方向上(即向着外围Al 原子的方向)失电荷, 说明相比于从Al 处吸引电荷, Ni 原子更易于从Re 处吸引电荷. 关于掺杂2个Re 原子, 在Ni3Al 超晶胞中,2个Re 原子的相对位置情况有三种, 设Ni3Al 超晶胞的边长为3a, 三种相对位置分别是2个Re 原子的间距为和然后分别计算三种情况的晶胞能量, 见表1.

图4 Re 掺杂后掺杂点位附近的差分电荷密度Fig. 4. The differential charge density around the doping position after Re substitutes.

表1 Ni3Al 超晶胞能量与2个Re 原子间距的关系Table 1. Relation between the energy of Ni3Al supercell and the distance between 2 Re atoms.
Ni3Al 超晶胞中掺杂的2个Re 原子间距越大,晶胞能量越小, 晶胞越稳定. 因此, 2个Re 在Ni3Al 中的最优掺杂位置为相距的两个Al 晶位, 即位于超晶胞的体对角线上且间距为体对角线的1/3, 说明Re 原子在Ni3Al 中是分散分布而非聚集分布.
3.2.3 Re 对Ni3Al 态密度的影响
从差分电荷密度图不能完全分析出成键情况,因此从态密度的角度进一步分析. 纯Ni3Al 体系和Ni3Al-1Re (掺杂1个Re 原子)体系的总态密度如图5 所示.
关于总态密度, 费米能附近主要的峰是由Ni-Al 键引起的. 通过图5 发现, 在费米能附近,Ni3Al-1Re 体系的峰略低于纯Ni3Al 体系的峰, 说明Re 的掺杂削弱了Ni-Al 键, 使得Ni-Al 键的键能降低, 此结论与3.2.1 节中所得结论一致. 为了进一步讨论Re 原子与体系中的Ni 或Al 原子发生的轨道相互作用, 分别计算了Re 原子、与Re 近邻的Ni 和Al 原子的局域态密度.
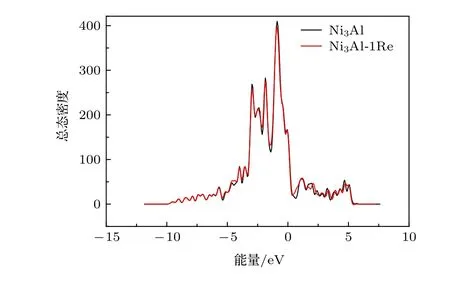
图5 纯Ni3Al 和Ni3Al-1Re 体系的总态密度Fig. 5. The total density of states of Ni3Al and Ni3Al-1Re.
通过图6(a)可以分析, 在Re 原子掺杂前后,Re 的局域态密度的变化. Re 加入后, Re 原子的5d 轨道相比于其他轨道变化明显, 并且5d 轨道的局域态密度在约–4.5 和0.75 eV 处形成峰值, 说明在这两个能量附近存在较多的电子分布, Re 加入后与体系中其他原子发生相互作用.
关于与Re 近邻的Al 的局域态密度, 如图6(b)所示, 在Re 原子局域态密度出现峰值的区域, 只有Al 的3s 轨道在–4.5 和0.75 eV 处产生小峰, 但是变化幅度很小, 说明在Ni3Al-1Re 体系中,Re 的5d 轨道与近邻Al 原子的3s 轨道存在微小的相互作用.
图6(c)显示与Re 近邻的Ni 原子局域态密度,相较于Ni 原子的4s 轨道和4p 轨道, Ni 原子3d轨道的态密度值很大. 3d 轨 道 在 约–4.5 和0.75 eV 处出现小峰, 与Re 原子的5d 轨道在同一位置出现峰值, 而Ni 原子的4s 轨道和4p 轨道整体上变化很小, 且没有在–4.5 和0.75 eV 两个能量点处形成峰, 因此说明Re 掺杂Ni3Al 后, Re 的5d 轨道与邻近Ni 原子的3d 轨道存在相互作用.
3.3 Re 对Ni3Al 力学性质的影响
在微观结构方面, Re 掺杂后主要增强了与近邻Ni 原子间的相互作用, 并导致附近Ni—Al 键键能降低. 材料内部结构的变化往往会引起其力学性质的改变, 因此从弹性模量、热力学性质两方面探究Re 的掺杂对Ni3Al 金属间化合物力学性质的影响.

图6 Re, 与Re 近邻的Al 和与Re 近邻的Ni 的局域态密度 (a) Re 原子在纯Re 和在Ni3Al-1Re 中的局域态密度;(b)与Re 近邻的Al 在Ni3Al 和Ni3Al-1Re 中的局域态密度;(c)与Re 近邻的Ni 在Ni3Al 和Ni3Al-1Re 中的局域态密度Fig. 6. Local density of states(LDOS) of Re, Al(next to Re)and Ni(next to Re): (a) LDOS of Re in pure Re and in Ni3Al-1Re; (b) LDOS of Al(next to Re) in Ni3Al and in Ni3Al-1Re; (c) LDOS of Ni(next to Re) in Ni3Al and in Ni3Al-1Re.
3.3.1 Re 对Ni3Al 弹性模量的影响
本小节主要计算了Ni3Al-1Re (掺杂浓度0.93%)、Ni3Al-2Re (掺杂浓度1.85%)和纯Ni3Al体系的弹性常数、体弹性模量、杨氏模量和剪切模量等.
为了更好地比较加入Re 原子前后的影响, 首先计算纯Ni3Al 的弹性常数c11,c12和c44. 对于立方晶系,c11,c12和c44是全部的弹性常数, 计算结果 为c11= 233.2 GPa,c12= 152.6 GPa,c44=118.1 GPa. 体弹性模量B, 剪切模量G, 杨氏模量E可由下面的公式计算:

将计算结果与其他研究的一些实验值和计算值进行对比, 结果如表2 所列.
由表2 可以看出, Ni3Al 的弹性常数和三种弹性模量与其他相关研究的计算值和实验值相差不大. 与纯Ni3Al 相比, 当Re 的掺杂浓度为0.93%时, 体弹性模量增加1.1%, 剪切模量增加1.0%, 杨氏模量增加1.0%; 当Re 的掺杂浓度为1.85%时,体弹性模量增加3.7%, 剪切模量增加3.3%, 杨氏模量增加3.2%, 说明Re 的掺杂能够增加Ni3Al 的刚性和硬度, 但是增加的效果不显著. 随着Re 掺杂浓度的升高, 增加效果呈上升趋势. 弹性性能是与合金的室温和高温强度都密切相关的最基本的性能, 因此Re 提高了Ni3Al 的刚性和硬度, 能够从一些实验研究结果上得以验证[24,25].
G/B值表征材料塑性变形的阻力, 该值越大材料越脆, 该值越小材料韧性越好[26]. 比较G/B值发现, 尽管Ni3Al-1Re, Ni3Al-2Re 与纯Ni3Al相比结果没有显著变化, 但是根据Pugh 的经验判据,G/B <0.57 的材料仍属于易延展材料. Pettifor的理论指出柯西压力值(c12-c44)可以用来描述金属间化合物中原子键的特征[27]. 柯西压力值越小,共价键的方向性越强, 材料越脆. 根据表2, Re的掺杂浓度为0.93%时, 柯西压力值增加0.4; 掺杂浓度为1.85%时, 柯西压力值降低0.8, 说明在Ni3Al 超晶胞中掺杂1个Re 导致Ni3Al 韧性增加, 而掺杂2个Re 导致Ni3Al 韧性降低. 关于Re的掺杂增加Ni3Al 脆性的结论, 与某些研究结果一致[14].
3.3.2 Re 对Ni3Al 热力学性质的影响
为了探究在不同温度下Re 对Ni3Al 力学性质的影响, 对第一性原理计算结果进行温度修正, 论文采用声子谱计算对纯Ni3Al 晶胞和掺杂1个Re 原子的Ni3Al 晶胞的熵、自由能和定体热容进行计算. 另外, 采用了准谐波近似方法计算未掺杂晶胞和掺杂晶胞的体弹性模量B和热膨胀系数α,进而比较Re 的掺杂对Ni3Al 金属间化合物热力学性质的影响.

表2 Ni3Al 弹性常数和弹性模量的计算值与其他研究的计算值和实验值的对比以及Ni3Al-1Re, Ni3Al-2Re 弹性常数等物理量的计算值Table 2. Comparison of calculated values of elastic constant and modulus of Ni3Al with other calculated, experimental values and calculated values of some physical parameters of Ni3Al-1Re and Ni3Al-2Re.
由图7(a)可以看出, 在温度区间为[0, 1650 K],Ni3Al-1Re 的熵总是略大于未掺杂晶胞. 一般固体的熵来自晶格振动所引起的各种量子态[28], 掺杂Re 后, 增加了体系内原子在原晶格上的排列方式,进而增加了系统中振动的微观态数目. 根据(12)式, 有

式中S为晶胞的熵,W为系统中包含微观态的数目,k为玻尔兹曼常量. 当系统中振动的微观态数目增加时, 系统的熵也随之增加.
图7(b)为Ni3Al 和Ni3Al-1Re 的自由能随温度的变化曲线. 由图7(b)可知, 掺杂晶胞的自由能略小于未掺杂晶胞. 此处的自由能为亥姆霍兹自由能, 关于亥姆霍兹自由能可定义如下:

式中F为晶胞的亥姆霍兹自由能,U为晶胞的内能,T为温度,S为晶胞的熵. 在0 K时, 掺杂晶胞的自由能比未掺杂晶胞的自由能低(UNi3Al(0 K) =428.95 kJ/mol,UNi3Al−1Re(0 K) = 419.76 kJ/mol),说明掺Re 晶胞的内能较低, 这是因为Re 的掺杂使得原子之间的结合更加紧密有效. 随着温度的升高,TS项对(13)式的影响增大, 并且Re 掺杂后产生了额外的混合熵, 因此在高温时, 掺Re 晶胞的自由能低于未掺杂晶胞的自由能. 当自由能为负值时, 系统开始对外做功. 掺Re 晶胞自由能的绝对值始终大于未掺杂晶胞, 说明掺Re 晶胞对外做的功大于未掺杂晶胞.
根据图7(c)可知, Re 掺杂后, 晶胞的定体热容与未掺杂时相比几乎不变. 在德拜理论中, 通过分析晶格的振动模计算热容量, 每一个振动模的热容量只取决于它的频率, 而整个晶胞的热容量是许多个振动模的热容量在频谱上的积分. 因此, 说明Re 掺杂后的Ni3Al 在受热过程中所产生的振动频率与纯Ni3Al 相比相差不大.
计算Ni3Al-1Re 的体弹性模量和热膨胀系数时, 考虑温度区间为[0, 1900 K], 1900 K 为目前航空发动机所能达到的最大涡轮前温度. 在图7(d)中, 计算的Ni3Al 体弹性模量随温度的变化趋势与实验结果一致[23]. Re 的掺杂增加了Ni3Al 的体弹性模量. 在低温时, Ni3Al-1Re 的体弹性模量略大于Ni3Al, 而在高温时, Ni3Al-1Re 的体弹性模量远远大于Ni3Al. Ni3Al 的体弹性模量随温度的升高而降低, 这是因为温度的升高使得晶胞中的原子产生更大的动能, 导致原子更易于偏离其平衡位置,而弹性模量表示使原子离开平衡位置的难易程度[29],因此温度的升高使得Ni3Al 的体弹性模量降低. 掺杂Re 后, 体弹性模量没有随温度的升高而明显降低, 说明Re 不易使Ni3Al 晶胞内的原子偏离其平衡位置, Re 增强了Ni3Al 中原子间结合力.
图7(e)为Ni3Al 和Ni3Al-1Re 热膨胀系数随温度的变化曲线, 其中Ni3Al 的计算结果与实验结果符合得较好[14]. Ni3Al 晶胞的α随温度的升高而增加, Ni3Al-1Re 晶胞的α在600 K 以下变化趋势与Ni3Al 基本相同, 但是在高温段时,α开始缓慢下降并明显低于Ni3Al 的α, 说明Re 的掺杂降低了Ni3Al 体积对于温度的敏感性. 随着温度的升高, Ni3Al-1Re 的体积膨胀得没有Ni3Al 明显, 从而掺Re 晶胞内原子间距增大的程度也不明显, 原子间结合力得以保持, 进而弹性模量减小的程度较小, 这也与Ni3Al-1Re 晶胞的体弹性模量在高温段没有出现明显减小趋势的结论相符合.
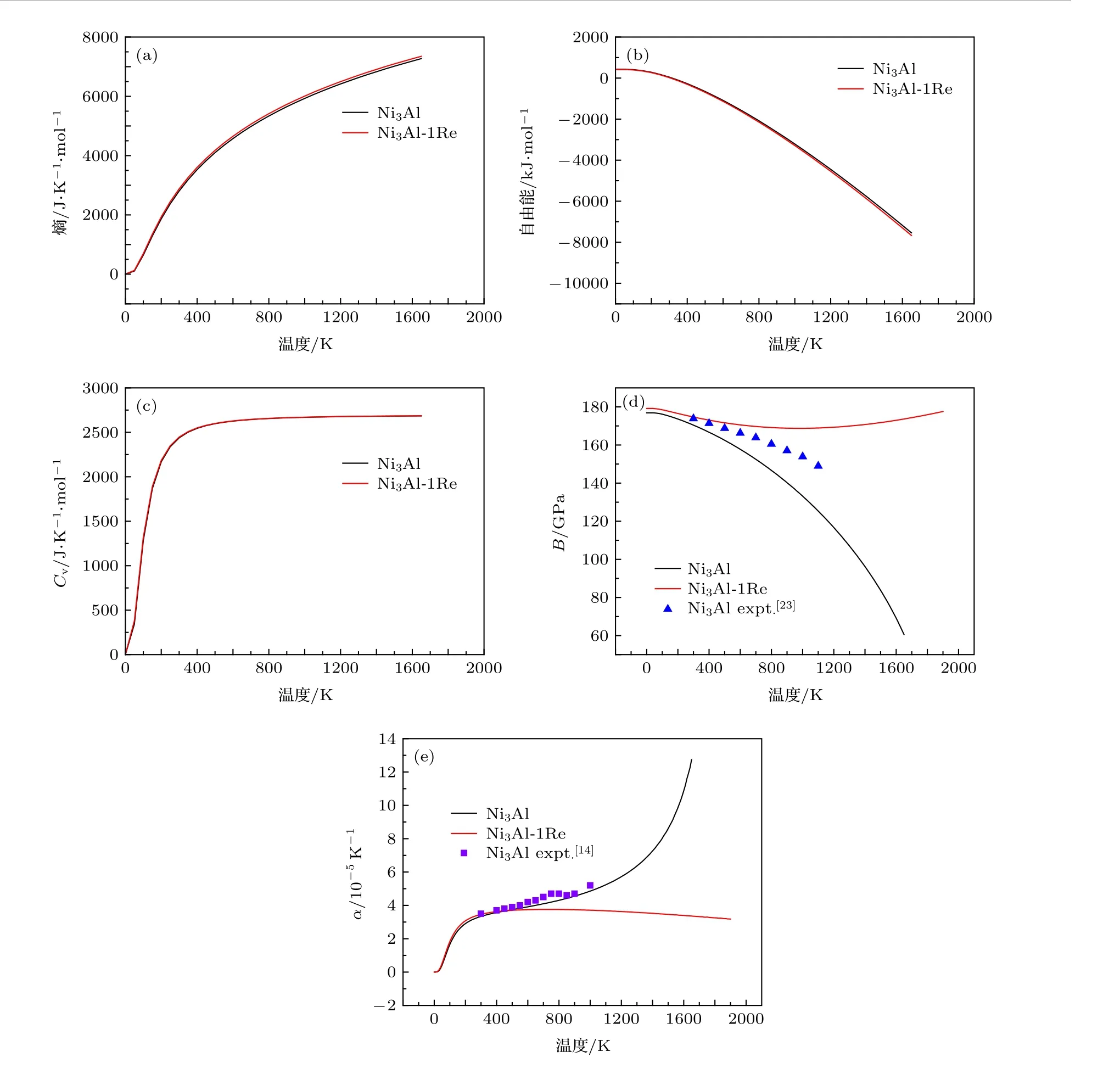
图7 Ni3Al 和Ni3Al-1Re 的热力学性质随温度的变化曲线 (a) Ni3Al 和Ni3Al-1Re 的熵随温度的变化曲线; (b) Ni3Al 和Ni3Al-1Re 的亥姆霍兹自由能随温度的变化曲线; (c) Ni3Al 和Ni3Al-1Re 的定体热容随温度的变化曲线; (d) Ni3Al 和Ni3Al-1Re 的体弹性模量随温度的变化曲线; (e) Ni3Al 和Ni3Al-1Re 的热膨胀系数随温度的变化曲线Fig. 7. Thermal properties of Ni3Al and Ni3Al-1Re as a function of temperature: (a) Entropy of Ni3Al and Ni3Al-1Re as a function of temperature; (b) Helmholtz free energy of Ni3Al and Ni3Al-1Re as a function of temperature; (c) C V of Ni3Al and Ni3Al-1Re as a function of temperature; (d) B of Ni3Al and Ni3Al-1Re as a function of temperature; (e) α of Ni3Al and Ni3Al-1Re as a function of temperature.
4 结 论
本文主要研究了Re 对Ni3Al 金属间化合物微观结构和力学性质的影响. 对于Re 在Ni3Al 超晶胞中不同位置溶解能的计算表明, Re 原子易于替代Ni3Al 中的Al 位. Re 掺杂后引起Ni3Al 晶格常数小幅度地增大, Re 主要与近邻的Ni 原子成键,并使得附近Ni—Al 键键能降低. 通过分析差分电荷密度图得出, Re 的掺杂增强了与近邻Ni 原子的相互作用. 进一步通过态密度图分析得知, Re 原子的5d 轨道与邻近Ni 原子的3d 轨道存在相互作用, 并且该5d 轨道与邻近Al 原子的3s 轨道存在微小的相互作用. 对弹性常数和模量的计算表明掺杂浓度为0.93%的Re 增强了Ni3Al 的硬度和刚性, 但是增强效果不显著. 利用柯西压力值(c12–c44)判断得知, 当Re 的掺杂浓度为0.93%时, Ni3Al 的韧性得到改善. 随着掺杂Re 原子的浓度增加,Ni3Al 的硬度和刚性增强的程度越大, 但是当Re 的掺杂浓度为1.85%时, 降低了Ni3Al 的韧性.在热力学性质方面, Re 的掺杂增加了Ni3Al 的熵和体弹性模量, 尤其在高温下, 体弹性模量的增加较为显著. 同时Re 降低了Ni3Al 的自由能和高温下的热膨胀系数. 此研究可为提高航空发动机涡轮单晶叶片的力学性能提供理论依据.
