评估新型冠状病毒地区防控效果的一种近似方法
2020-06-04李冀鹏洪峰白薇廖敬仪张彦如周涛
李冀鹏 洪峰 白薇 廖敬仪 张彦如 周涛†
1) (电子科技大学大数据研究中心, 成都 611731)2) (清华大学深圳国际研究生院, 深圳 518055)(2020年3月14日收到; 2020年5月15日收到修改稿)
我们观察到地区累计确诊的病例数目和武汉封城前流入的人口总数高度相关, 且本地第三代感染者占比很小. 基于此, 提出了一种考虑输入病例和地区人口效应的定量化评估新型冠状病毒地区防控效果的近似方法, 并将其用于评估武汉流出人口前50 的城市防控的成效. 防控效果最显著的10个城市依次是石家庄、洛阳、恩施、周口、厦门、贵阳、咸宁、安庆、信阳、南宁.
1 引 言
新型冠状病毒(COVID-19)在世界范围内迅速流行,对人类健康和全球经济发展造成了不可估量的影响[1−5]. 估计一种传染病传染能力最重要的参 数 是 基 本 再 生 数R0(basic reproduction number), 指在一个全是易感染态个体构成的群体中, 一个感染态的个体在恢复之前平均能感染的人数[6]:R0> 1 表示有流行病爆发的可能,R0< 1 则表示疾病难以传播. 早期的分析显示, COVID-19 的基本再生数所属区间约为[2.0, 4.0], 例如2.47—2.86[1], 1.4—3.9[7], 2.39—4.13[8], 2.0—3.3[9],1.5—3.5[10], 2.88—3.67[11], 1.4—3.8[12]. Zhou等[13]
假设COVID-19 早期传播可以用一个SEIR 动力学模型近似刻画, 且自由传播时呈指数趋势, 估计基本再生数为2.8—3.9, 后根据最新的流行病学特征参数修正为2.2—3.0. 宋倩倩等[14]用指数增长法、最大似然法和SEIR 模型分别对R0进行了估计, 其估计区间分别为3.63—3.87, 2.90—3.43和3.71—4.11. 总体来说, 新型冠状病毒肺炎属于具有中-高等级传播能力的传染性疾病, 最近全球范围内的快速爆发也验证了这一结论.
2020年1月20日, 中华人民共和国国家卫生健康委员会发布公告, 将新型冠状病毒肺炎纳入《中华人民共和国传染病防治法》规定的乙类传染病, 并采取甲类传染病的预防、控制措施. 随后,各省市自治区出台了有力的防控措施, COVID-19 的传播经历了短暂的高峰之后迅速在中国得到遏制. 定量化评估一个地区防控的效果具有非常重要的意义—既有助于我国流行病学专业人士和相关管理人员比较性地回顾总结得失, 又可以为依然饱受病毒肆虐的海外地区提供参考. 为了评价防控措施的效果, 通常采用有效再生数对传染病在采取了防控措施(非自由传播状态)下的传播能力进行实时评估. 有效再生数Rt定义为在某时刻t, 一个感染者平均而言可以感染其他个体的数量[6], 如果有效再生数下降到1 以下, 就说明该传染病已经处于可控的状态. Zhang 等[15]分析了湖北之外若干地区的有效再生数, 发现均在一月底之前降到了1 以下. Chen 和Zhou[16]以1月21日为全国强有力防控措施的起点, 通过计算有效再生数, 发现绝大部分省份在1月21日之后一周以内, 有效再生数就下降到1, 湖北的有效再生数也在2月2日下降到1 以下. 陈端兵等[17]进一步的分析显示, 经历了短暂的爆发增长后, 韩国的有效再生数也于2月25日下降到1 以下. 尽管有效再生数可以在疾病传播过程中反映当前控制的效果, 但依然不适于作为一个地区防控效果的总体指标. 这是因为有效再生数是一个时间序列, 而我们很难直接比较两个时间序列, 除非某序列的取值一直低于或者高于另外一个序列. 文献[15−17]暗示可以用有效再生数降到1 的时间来衡量防控效果. 这有明显的实用价值, 但是作为事后评估是不公平的, 因为不同地区人口密度、人口结构和生活工作习惯可能存在重大差异, 因此在传染病自由传播时期的基本再生数就可能存在显著差异. 另外一种直观而又简单的方式, 就是直接用地区的累计确诊人数或者累计确诊者占地区总人口的比例(确诊比例)作为防控效果的指标. 前者显然是不合适的, 因为不同地区人口总数差异很大; 后者表面合理, 实际上也不公平,因为不同地区与武汉“亲疏有别”, 输入病例数目相差很大, 如果只看确诊比例, 那么与武汉人员来往越少, 防控效果就越好.
本文拟提出一种可以量化评估一个地区防控效果的方法. 我们的基本思路是根据COVID-19 在中国传播的特征和流行病动力学的机制, 推断影响一个地区流行病传播的普适规律并把它们看作不可控的因素. 利用数据分析的方法剥离这些不可控因素后, 剩余的差异部分就被认为是不同控制效果导致的, 从而可以用这些差异来评估一个地区防控的效果.
2 方 法
在介绍具体的方法和假设之前, 我们先指出两个重要的事实. 第一, 各地区确诊人数很大程度上受到了武汉封城前流入人口的影响[18−20]. 表1 列出了武汉封城前2 周流入人口前50 名的城市的流入人口数(按照流入人口数排序)、常住人口数和截止到2020年2月25日的累计确诊数(后面零星确诊案例可以忽略). 图1 显示了这50个城市武汉流入人口数和累计确诊数的关联, 可以看到, 两者几乎是线性关系, 相应的Pearson 关联系数高达0.9705. 第二, 不同地区确诊病例中的相当一部分是输入病例, 例如Zhang 等[15]采集的有详细信息的湖北外8579 例病例中, 截止到2月17日, 有42.80%在武汉或除武汉外湖北其他地区有过暴露史. 能够获取较完整病例数据的地区, 例如深圳、四川等地, 均有1/3—1/2 病例系输入病例—绝大多数来源于武汉和除武汉外湖北其他地区, 少数来自于其他省、市、自治区. 如果将输入病例视作第一代, 输入病例在本地的感染者视作第二代, 第二代感染的病例视作第三代, 则第三代及以上的感染者是少见的.
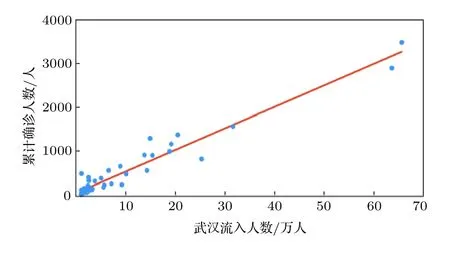
图1 武汉流入人口最多的50个城市的累计确诊数(人)与武汉流入人口数(万人)之间的关系. 其中数据点代表城市, 红色直线代表线性拟合的结果(R2 = 0.942)Fig. 1. The relationship between the cumulative number of confirmed cases in the top-50 cities with maximum inflow population from Wuhan and the number of corresponding inflow people. Cities are represented by data points and the linear fitting is represented by the red line (R2 = 0.942).
基于以上事实, 我们忽略一个地区三代以及三代以上的感染者, 则一个地区最终的累计确诊人数主要由两部分组成: 一是输入病例(包括武汉和其他地区, 但以武汉为主), 二是由输入病例直接引起的本地传播. 根据仓室模型, 后者应该与输入病例和本地常住人口(易感人群数量)的乘积成正比[6,21].记地区i的累计确诊人数为Ni, 可得:

其中u是待定参数, 大约是武汉封城前人口感染比例(武汉封城前出现了人口流出的峰值, 具体请参见文献[18]),Ai是从武汉流入地区i的人口数,Pi是地区i的常住人口数. 需要计算的关键量是控制参数ci, 它标志了地区i防控措施的效果.ci值越小, 说明地区i的防控成效越显著. 显然, 这种全接触的假设太过简单, 例如对于千万人口的大城市, 任何人都不能接触到所有人口, 而只能接触到很少一部分人[22]—如“顿巴数”所暗示的[23,24], 一个人具有紧密关系的人是非常有限的. 事实上, 在很多关于流行病传播动力学的研究中, 每一个染病者单位时间能够接触的易感者人数被假设与该个体活动区域的易感人口无关, 而是一个常数[25−27].在这种情况下, 一个地区i的确诊人数可以近似为

表1 武汉封城前2 周流入人口前50 的城市名称、流入人口数、常住人口数、截止到2020年2月25日的累计确诊人数、控制因子c 的取值以及利用本文方法所得到的防控效果的排名. 武汉流入人口统计的是2020年1月10日至1月22日离开武汉的人数, 数据来源于“百度迁徙”. 常住人口数取自第六次全国人口普查数据(http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm)Table 1. The six columns respectively show the names of the top-50 cities with maximum inflow population from Wuhan during the two weeks before the closure, the inflow population, the permanent resident population, the cumulative number of confirmed cases as of February 25, 2020, the values of the controlling parameter c, and the rankings of the control efficacy by the present method. The inflow population accounts for the number of people who left Wuhan from January 10 to January 22, 2020, obtained from “Baidu Migration”. The number of permanent residents is taken from the sixth national census (http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm).
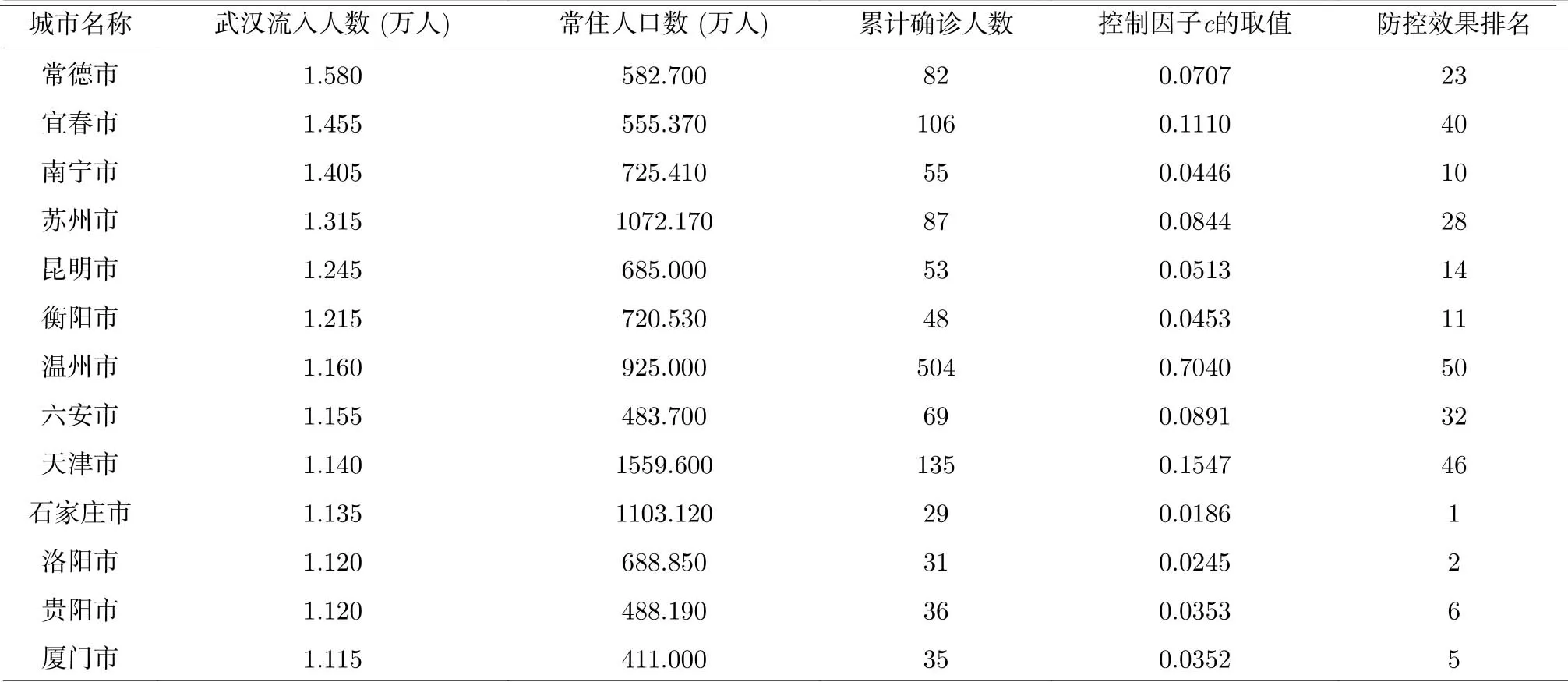
表1 (续) 武汉封城前2 周流入人口前50 的城市名称、流入人口数、常住人口数、截止到2020年2月25日的累计确诊人数、控制因子c 的取值以及利用本文方法所得到的防控效果的排名. 武汉流入人口统计的是2020年1月10日至1月22日离开武汉的人数, 数据来源于“百度迁徙”. 常住人口数取自第六次全国人口普查数据(http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm)Table 1 (continued). The six columns respectively show the names of the top-50 cities with maximum inflow population from Wuhan during the two weeks before the closure, the inflow population, the permanent resident population, the cumulative number of confirmed cases as of February 25, 2020, the values of the controlling parameter c, and the rankings of the control efficacy by the present method. The inflow population accounts for the number of people who left Wuhan from January 10 to January 22,2020, obtained from “ Baidu Migration” . The number of permanent residents is taken from the sixth national census(http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/indexch.htm).
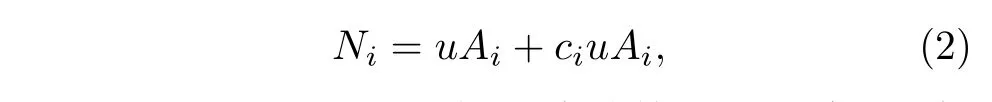
(1)式和(2)式中的ci都是待计算的控制参数, 但是取值显然不同. (1)式和(2)式都是极端的简化,尽管在人口密集的大城市中一个感染者不可能和所有易感人口接触, 但相比小城市或者乡镇, 他有更多机会通过聚集居住的小区、公共交通和商场超市等场所和更多人接触. 事实上, 在流行病仿真模型中, 人口密集的大城市中平均每个人产生的接触也更多[28,29], 因此我们认为真实情况应该介于两者之间, 即:

其中a是一个[0, 1]区间中的自由参数, 当a=1时方程(3)退化到方程(1), 当a= 0时方程(3)退化到方程(2). 显然, 如果能确定u和a的取值, 就可以通过公式
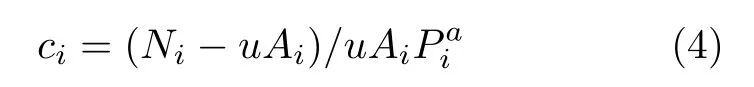
计算出每个地区i的控制参数ci, 进而对不同地区防控的效果进行评价.
3 结 果
首先估计u的取值. 2020年1月26日, 湖北省人民政府新闻办公室就新型冠状病毒感染的肺炎疫情防控工作召开了新闻发布会, 武汉市长周先旺表示: 受春节和疫情影响, 目前有 500 多万人离开武汉, 还有 900 多万人留在城里. 武汉2019年统计的常住人口是908 万人, 考虑到本文所有计算都选用常住人口数(春节大量流动人口返乡), 且武汉常住人口数和周先旺的表述基本一致, 本文选择武汉封城后人口为908 万. Li 等[30]估计武汉封城前两周, 即从1月10日到1月23日, 武汉累计新增感染人数为13118 人(95%置信区间为[2974,23435]), 则封城前后感染率大约为0.1445%, 所以可以认为u≈0.001445(所有变量以“人”为单位).根据Zhang 等[15]的报告, 截止到2月17日, 湖北省外在武汉或者除武汉外的湖北其他地区暴露过的输入病例占比为42.80%. 因为武汉1月23日后封城, 故2月17日之后出现症状的武汉输入病例可以忽略不计. 根据国家卫健委的公开数据, 2月17日湖北省外累计确诊病例数为12447 人, 2月25日湖北省外累计确诊病例数为12877 人. 因此在本文数据分析的时间点2月25日, 在武汉或者除武汉外湖北其他地区暴露过的输入病例占比约为0.428 × 12447/12877 = 41.37%. 考虑到本文分析的是武汉的输入病例数, 要从上述数字中去掉在除武汉外湖北其他地区暴露的病例, 因此我们估计这个比例应该在30%—40%之间. 如果根据从武汉流入人口最多的50个城市的数据为基础(表1),以公式

来估计, 则u的取值应该在区间[0.001436, 0.001915].两种方法(数据来源于两篇不同文献[15,30])获得的u的取值具有相当的一致性. 考虑到估计比较粗糙,我们取两位有效数字, 即u= 0.0014.

图2 双对数坐标下(Ni – uAi)/uAi 与Pi 的关联关系. 其中数据点代表城市, 红色直线代表线性拟合的结果(R2 =0.141), 拟合的斜率是0.234Fig. 2. The correlation between (Ni – uAi)/uAi and Pi in the log-log coordinates, where data points represent cities and the red line represents the linear fitting (R2 = 0.141).The fitting slope is 0.234.
至此, 我们认为, 对于各地区最终的确诊人数而言, 输入病例数是最主要的因素, 有很强的解释作用; 当地的人口数(大约是人口数的1/4次方)是次要的因素, 也具有一定的解释作用. 控制掉这两个因素后, 各地区存在的差异, 也就是ci取值的大小, 就可以反映各地区防控的效果. 基于估计的u值和a值, 利用(4)式计算得到各地区的ci值, 并按从小到大排序, 得到的控制效果排名即为表1 的最后一列. 根据我们的计算结果, 防控效果最好的10个城市(从最好往下排序)依次是石家庄、洛阳、恩施、周口、厦门、贵阳、咸宁、安庆、信阳、南宁; 防控效果最差的10个城市(从最差的往上排序)依次是温州、深圳、广州、仙桃、天津、鄂州、南昌、阜阳、杭州、十堰.
以上通过假设各ci相同来估计a值的方法是很粗糙的(实际上我们又要用这个估计的a值来算出不同取值的ci), 因此以a= 0.234 为中心, 就a的不同取值对最终排序结果的影响进行了敏感性分析. 给定两个不同的a值a1,a2, 以及对应的两个排序X1,X2, 我们用Kendall’s Tau 值[32]来刻画排序X1和X2之间的相近程度. 本文考虑50个城市, 则会形成1225个城市对. 依次考察这1225个城市对, 如果某对城市i,j在X1和X2中是同序的(i在X1和X2中排名都高于j, 或i在X1和X2中排名都低于j), 则加1分; 如果它们在X1和X2中是逆序的(i在X1中排名高于j但在X2中排名低于j, 或i在X1中排名低于j但在X2中排名高于j), 则减1分. Kendall‘s Tau 值就是总分除以1225. 如果Tau 值为1, 则说明两个排序完全一致; 如果Tau 值为–1, 则说明两个排序完全相反.从图3 可以看出, 在以a= 0.234 为中心的一个相当大的范围内, 这个排序是相当稳定的——所有其他排序与a= 0.234 对应排序之间的Tau 值都大于0.8. 基于此, 我们认为a= 0.234 对应的排序结果具有一定的参考价值. 如果考虑每一个输入病例接触的易感者数目是一个常数[25−27], 即a= 0, 则得到的城市排名和a= 0.234 对应的排名的Kendall’s Tau 值为0.827, 具有高度的一致性. 举例而言,a= 0 对应排名前10 的城市为石家庄、恩施、洛阳、厦门、贵阳、咸宁、周口、潜江、安庆和信阳, 其中有9个城市都和a= 0.234 对应排名重合.

图3 不 同a 值所得到的50个城市防控效果排序的Kendall’s Tau值Fig. 3. Kendall's Tau between rankings of control efficacy for different a.
4 讨 论
本文的分析显示石家庄的防控效果最佳. 我们认为取得如此出色的成绩有四方面主要的原因. 一是石家庄具有发达的制药业和纺织业, 提供了疫情攻坚战亟需的基础防疫物资. 石家庄有一百多家药企, 抗生素和维生素产量全球领先, 石家庄也是全国纺织基地之一, 其中仅汇康日用品有限公司的防护口罩日产量在疫情初期就达到了80 万只. 二是石家庄是武汉外最早开展全民摸排的城市, 在1月21日就对全体居民进行了摸排, 特别关注湖北迁入人员和出现新冠肺炎类似感染症状的居民. 石家庄抓住了“防止外来输入病例, 控制传染源”这一疫情初期防控措施的关键, 有效阻断了这些潜在的传染链条. 三是石家庄老百姓对疫情非常重视, 配合程度高. 在“信用石家庄”网站公布的疫情处罚公示和疫情失信名单上未出现一例个人, 均为超市和药房. 2月25日前石家庄新闻报导中仅出现一位女士因为未佩戴口罩和小区保安争吵. 四是石家庄特别重视重点地区(例如交通枢纽和人口密度大的居住区域)的消毒和医废处理, 动用了无人机等新技术手段提高消毒的覆盖率和频率. 与石家庄相比, 温州之所以防疫效果不佳, 除了基础防疫物资条件不足外, 还归咎于政府前期重视程度和宣传力度不足, 造成市民对防疫工作的配合度也相对较差—温州本地新闻中有多人多起暴力反抗检疫和拒不配合隔离的恶性事件, 以及基层干部自身不配合检疫措施的事件. 根据“信用温州网”公布的信息, 截止2月20日, 温州共有254 人因不配合疫情相关政策而失信. 在2003年非典疫情阶段, 石家庄是重灾区, 确诊患者达33 人, 而温州仅有1 人, 因此政府和老百姓对于类似公共卫生事件的应急处置经验以及重视程度或有不同. 从流行病学的角度看, 政府早期的重视, 特别是全面摸排(尽早发现可能的感染者), 以及通过宣传和防控措施加强对老百姓的引导(减少人与人之间的接触), 是快速高效控制疫情的关键. 希望石家庄的经验能够成为未来我国及其他国家和地区处理相似公共卫生事件的参考.
本文的方法也具有一些局限性. 首先, 没有考虑三代以上的感染者, 因此这种方法并不适用于评价武汉与国外其他疫情严重的地区. 事实上湖北部分受疫情影响严重的城市, 三代及以上的感染者数目不在少数. 其次, 不管是(1)式的仓室模型还是修正后的(3)式, 都暗含了平均场的假设, 而实际的传播是具有非常明显的聚集性[33]. 我们注意到图2 的关系暗示一个人能够在城市中产生的密切接触数与城市人口规模正相关, 大体上和城市人口之间是1/4次方的关系. 这是合理的, 因为大城市提供了更多大量人群聚集和接触的设施, 但是这些设施的数目不是和城市人口规模成正比, 而是呈亚线性的幂律关系[34]. 尽管这个数值本身具有直观的合理性, 但是我们估计a值的方法很粗糙, 实际上, 应该通过外在的方法确定a的取值. 使用健康码形成的带有时空位置信息的“亮码/扫码”数据来量化分析不同规模和社会经济发展水平下城市人口的流动和接触模式, 从而确定a值. 我们多次呼吁政府在进行数据脱敏(人员和地点匿名化)后开放这部分数据, 并已经获得了多个城市的支持—这部分数据不仅可以用于确定a值, 还可以用于建立流行病动力学的仿真模型, 从而更好预测传播趋势和预估政策效果. 总体来说, 本工作是以传播动力学机制为出发点, 尝试定量化评估地区传染病防控效果的有益尝试, 尽管还存在一些局限, 但我们相信本文报导的结果对于评价城市防控效果是有一定借鉴意义的. 与此同时, 需要提醒读者, 本文结果尚属于学术探索的阶段性成果, 不宜作为政府或者相关管理结构对地区防控情况评估的官方参考.
