基于ARMA模型的公路货运量预测及分析

惠倩倩

摘 要：为了把握公路货运量的变化趋势及公路货运市场的发展动向，从公路货运量预测及时间序列分析的相关原理出发，详细论述如何应用ARMA模型进行公路货运量的定量预测。以陕西省2010—2017年公路货运量月度数据为基准，判断其是否满足平稳性要求，经数据平稳化和标准化，构建出满足AIC和SC准则且通过残差分析监测的移动平均模型，最终将确定的模型应用到对2018年其他月份的公路货运量预测中。结果表明，预测结果接近真实值且误差和置信区间均在合理范围内，可以为公路货运市场的相关管理决策提供相应的支撑。

关键词：公路货运量;时间序列分析;预测;ARMA 模型

中图分类号：F540.3        文献标志码：A      文章编号：1673-291X（2020）12-0035-03

引言

近年来，随着物流行业和车货匹配平台的快速发展，我国公路货运市场规模已超过6万亿。准确把握公路货运量等发展趋势，可以为相关决策提供依据。公路货运量的预测是指基于公路货运市场过去的情况、当前的货运需求以及影响需求的相关因素间的关系，结合经验判断及各类定性、定量模型，对其变化趋势进行预测。时间序列作为定量预测的常用方法，在承认事物发展延续性的前提下，基于已有时间序列的变化模式来预测未来的变化。

鉴于自回归移动平均（ARMA）模型的广泛适用性及其在谱估计精度上的优越性，本文选用该方法对公路货运量进行预测。

一、预测原理

ARMA模型以不同时间下的观察值为时间序列，探索各个影响因素与预测对象间的回归关系，对其发展进行预测。考虑到各个影响因素带来的影响和预测对象自身变动的规律，ARMA模型可以表示为：

二、时间序列在公路货运量预测中的应用分析

本文以2010—2017年陕西省公路货运量为样本（见表1）。以前7年的历史数据为观测值序列，构建模型，得到2017年各月货运量的预测结果，并与2017年实际数据做比较，确定最佳的预测模型，最后预测2018年的公路货运量。模型的建立与预测都在EViews8.0中完成。

1.平稳化处理。为判断数据的平稳性，使用EViews软件，将2010—2016年陕西省公路货运量的历史数据定义为随机序列X。序列X呈现出了明显季节性和长期趋势，是一个不稳定的时间序列，需要采取差分运算直到差分后的数据为平稳序列。鉴于差分运算的阶数特性，同时进行一阶差分和十二阶差分，生成了稳定的时间序列Xt。且通过白噪声检验，Xt属于平稳非白噪声时间序列，具有了提取有效信息做出进一步预测的价值。

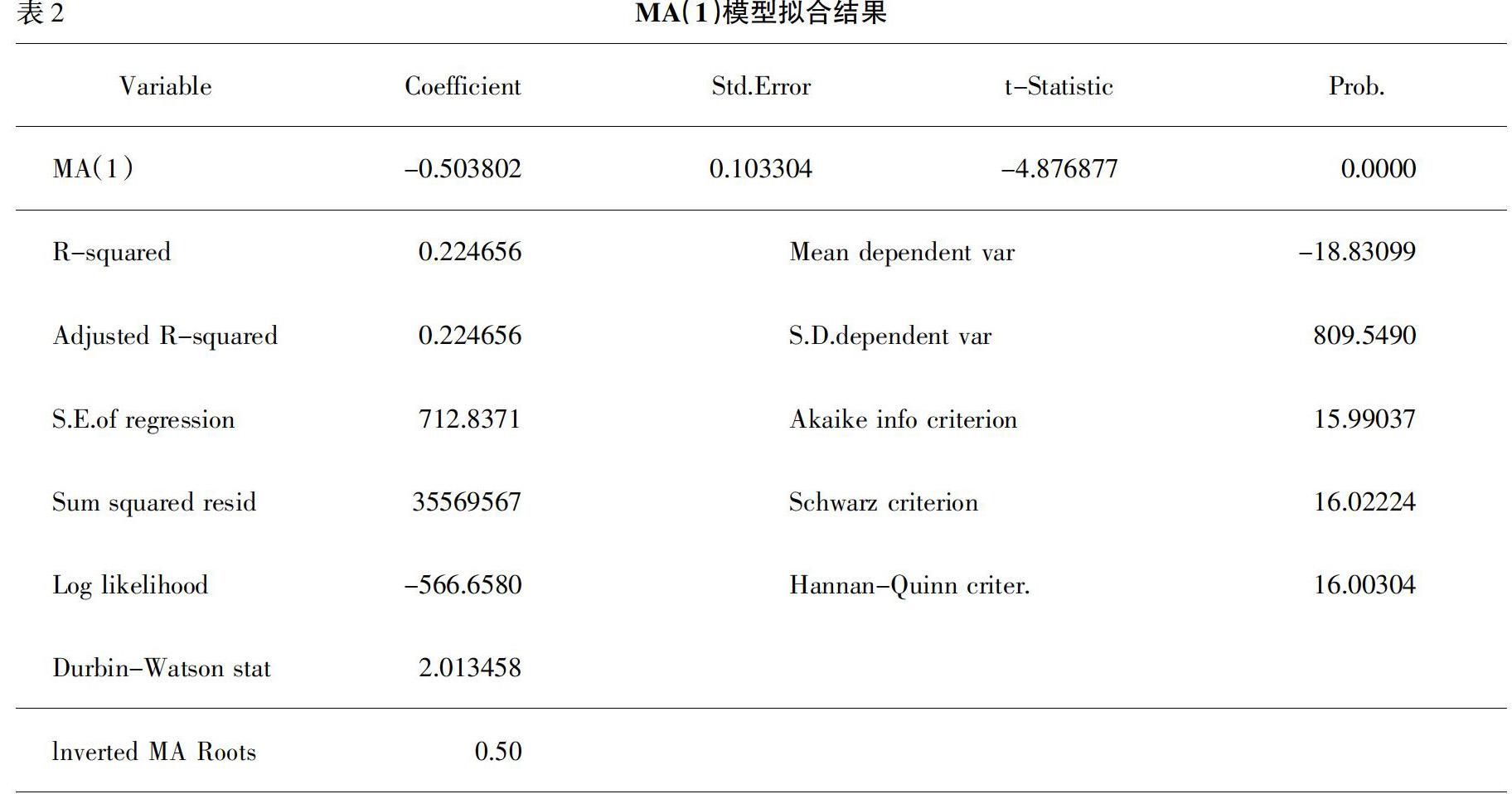
2.模型识别与建立。为了识别平稳、非白噪声序列Xt对应的ARMA模型参数，计算出自相关系数ACF和偏自相关系PACF。根据其ACF和PACF函数均具有一阶截尾的特性，可进一步构建ARMA（1，1）模型。通过方程估计，得到模型ARMA（1，1）的拟合结果。拟合结果中，AR（1）的Prob值小于0.05，但是MA（1）的Prob值远大于 0.05，即自回归和移动平均系数均不显著，拟合的效果仍有待提升。根据AIC和SC准则，经过多次试验，并综合比较了不同系数下的ARMA模型的可决系数和残差平方和，得到 MA（1）模型的拟合效果最为理想（如2表所示）。

3.模型检验。为评价模型的效果及准确性，尽可能使预测值与实际值的差距最小。本文基于MA（1）拟合结果的ACF及PACF，进行残差分析试验，确定残差序列的独立性。这表明，ACF函数及PACF函数完全满足2倍标准差范围的要求，Q-stat的Prob值也都大于0.05，这在一定程度上体现了MA（1）模型提取公路货运量信息的充分性。

三、模型预测

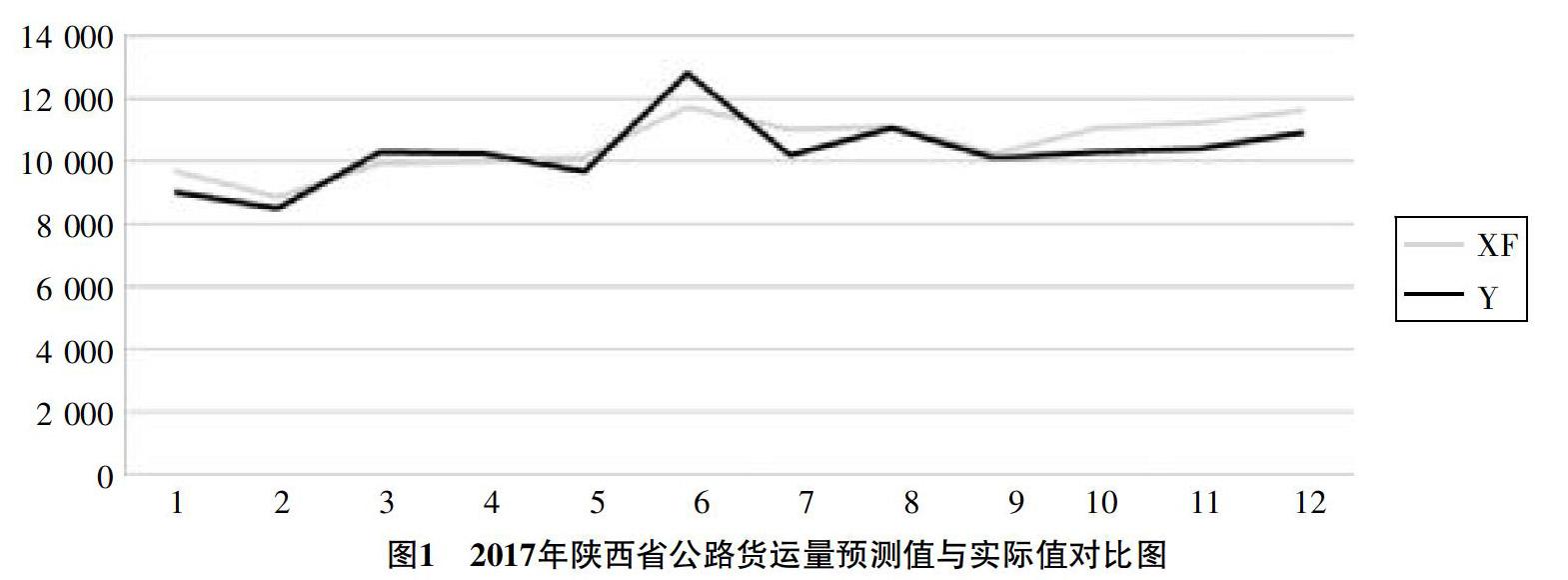
为检验模型的预测效果，本节以前7年各月公路货运量为观测序列，预测2017年的公路货运量，并与实际情况比较（如下页图1所示），其中XF、Y分别为预测值和实际值序列。可见，短期预测值与实际值的趋势基本一致，预测结果良好。但预测值整体上稍高于实际值，在预测精度上仍有提升空间。此外，时间跨度越大，二者的偏差也有所增大，主要是因为当前选定的预测原点是2016年12月的实际数据。

因此，在现实的运营管理决策中，应考虑预测值的时效性，及时更新数据信息，以最新数据为预测起点，尽可能减少决策偏差。模型预测结束后，可以根据预测结果，在置信区间内确定合适货运量及时掌握可能的市场需求。

四、最终预测及建议

本节利用确定的模型来预测2018年各月份公路运输货运量，为尽可能地减小预测误差，将2018 年3月份陕西省的公路货运货运量作为预测原点，得到其余几个月份对应的预测值。为观察各月的变化范围及趋势，识别公路货运量的季节性差异，图2给出了2018年公路货运量的变化趋势图。

结果表明，2018年各月的公路货运量基本趋于稳定。而2月的货运量最小，2月则处于明显的波谷状态，企业可以考虑适时地减少存货。并于6月达到月度货运量的峰值，其需求最大。此外，3月和8月呈现出两个小波峰，均属于货运旺季。由于春节即将来临，相较于前3个月，12月的公路货运量有明显上升。为满足市场需求，此时企业应适时增加库存量，管理部门应加强对货运市场秩序和安全的有效监管。

结语

本文根据历史数据，采用ARMA模型进行公路货运量的预测。结果表明，预测是可行有效的，且中短期的趋势拟合能达到较高的精度。然而，可获取的样本数据量是有限的，且没有一个模型是完美无缺的。时间跨度越大，预测结果偏离实际的可能就越大。我们必须及时掌握并更新样本数据，在提高样本质量的同时，改进预测方法，使预测效果最佳。

参考文献：

[1]  赵彦军，陈玉.时间序列分析方法在物流需求预测中的应用[J].物流科技，2017，（6）：12-14.

[2]  潘树龙，孙维夫.基于时间序列分析方法的物流总额预测研究[J].湖北民族学院学报：自然科学版，2015，（1）：114-116.

[3]  胡洁琼，李珍萍.基于时间序列的全社會货运量预测及分析[J].物流技术，2014，（5）：128-130.

[4]  葛蔚，魏海军.基于时间序列分析的物流企业运输量演化模式与案例研究[J].大连海事大学学报，2011，（2）.

[5]  邓爱萍.肖奔.基于时间序列的市场需求预测模型研究[J].科学技术与工程，2009，（23）：1.

[6]  田根平，曾应坤.基于时间序列模型在物流需求预测中的应用[J].物流科技，2007，（9）.

[7]  张世英，陆晓春，李胜朋.时间序列在城市交通预测中的应用[J].天津大学学报：社会科学版，2006，（5）：52-54.

[8]  李序颖，等.我国交通货物运输量的时间序列分析[J].系统工程理论与实践，2005，（1）：49-55.

[9]  黄丽.随机时间序列模型在物流需求预测中的应用[D].武汉：武汉大学，2004.