“预”防治衔接“立”生态学习——述小升初衔接中的关键点与纾困之策

郭海军

（厦门市海沧区东孚中心小学，福建 厦门 361027）

小学生进入初中普遍感到不适应，主要是由小学和初中的数学思想方法、课堂教学方法、学习程度要求的差异造成的，具体表现为：小学的研究对象主要是具体化的数字，初中主要是抽象化的符号；小学的运算主要是纯数值的具体化运算，初中主要是代数式的形式化运算；小学的解决问题主要是采用算术方法，初中主要是采用方程方法；小学的信息获取主要是依靠直观感知，初中主要是依靠逻辑推理；小学的猜想验证主要是依托不完全归纳法，初中主要是依托完全归纳法；小学的问题研究主要是关注解决具体问题的特殊技巧，初中主要是关注通性问题的通用方法；小学对数形结合的要求还停留在较低层次的凑合阶段，初中已经达到较高层次的融合阶段；小学的课堂教学主要还束缚在教师的循循善诱模式，初中则更多地倡导以学生自学为主的导学模式。

一、实现“三个转变”

为了使小学生能够迅速适应初中教学，小学数学教师首先必须树立全局观念，秉承“以防代治”和“可持续发展”的绿色教学理念，实现思想上的三个转变。

1.从“关注技巧”向“关注通法”转变

小学知识容量小，时间充裕，课堂有时间关注解决具体问题的特殊技巧。有些小学生不求甚解，靠记住解题技巧和经历题海战术，也能解决某类具体问题了，他们成了滥竽充数的优生。初中知识容量大，时间紧凑，课堂必须把时间花在关注解决通性问题的通用方法上，学生需要具备良好的数学思维和自学能力才能消化吸收。之前在小学能够滥竽充数的“优生”，由于思维和能力跟不上，必定要被无情地剥离出来，显现为“不适应的学生群体”。

以人教版六年级上册《（百）分数解决问题的整理和复习》为例，图1关注的是解决8类具体问题的特殊技巧，学生只要记住这些技巧，然后按图索骥就能解决问题。这其中不乏有些聪明的学生看出了门道，学习不再具有挑战性而变得索然无味，开始耍起了小聪明，变得不求甚解，思维和能力就此停滞不前，实在可惜。因此，建议小学教学不能只是停留在图1的层次，而应该提升到图2的层次：分数和百分数解决问题无非就是研究单位“1”的量、对应量、对应分率这三个量，利用三个量之间的关系“已知其中两个数，求第三个数”来解决问题。关注解决通性问题的通用方法，让数学学习变得具有挑战性：通性问题的多彩变换让数学世界变得更加神秘，通用方法的灵活运用让数学学习变得更有魅力。

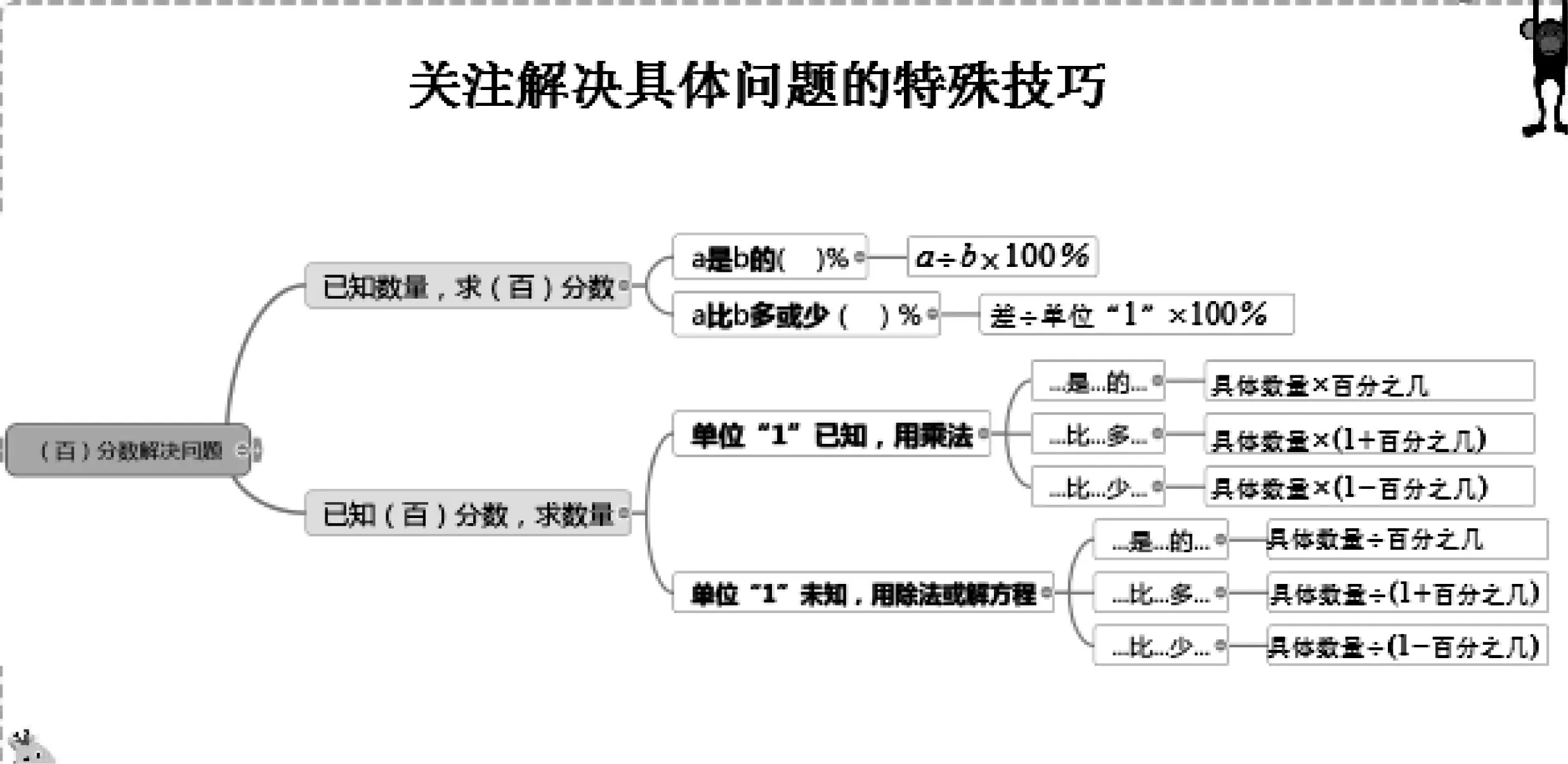
图1

图2

2.从“嚼碎喂食”向“导思自学”转变

小学特别是低段的课堂大都有一个通病：教师习惯把知识点嚼碎了一点一点喂给学生，生怕学生不消化；问题问得太多太细，而且同样的一个问题要反复讲，生怕学生不理解。学生独立思考的时间在无形中被挤占了，丧失了思维温度的课堂让学生对学习囫囵吞枣、对教师产生依赖心理。初中课堂一般采用“课前自学—课上答疑—课后练习”的模式，对学生的思维品质和自学能力有较高的要求。思维品质和自学能力在小学没有养成，进入初中自然不适应。因此，建议小学特别是高段教师，把浓缩提炼的核心问题以导学案的形式呈现给学生，启发学生自主思考，与初中进行无缝对接。

以人教版六年级下册《正比例和反比例的认识》为例，图3和图4的导学案根据教学重难点，浓缩提炼出核心问题，有利于学生对正比例和反比例的本质、区别和联系形成整体认识。既培养了学生的思维品质，又培养了学生的自学能力，与初中教学接轨。

图3

3.从“求快低效”向“归慢高质”转变

初中的代数问题较小学更加复杂，而且出现大量的几何问题，需要借助绘制示意图来帮助分析和解决问题。小学课堂过分依赖和滥用多媒体技术，片面追求快节奏和图便利，示意图大都只重视结果的“快”呈现，而忽视过程的“慢”生成。多媒体播放虽然快，但是转瞬即过且用过无痕。学生对示意图的形成过程走马观花，作图能力的培养是“低效”的。多媒体技术是一把双刃剑，对于学生作图能力的培养，多媒体的使用是快速低效，教师的板演则是慢速高质。建议凡是需要用到示意图的地方，教师都应该尽可能慢下来，采用亲自板演的方式，带领学生一同经历示意图的生成过程，掌握绘制示意图的能力。

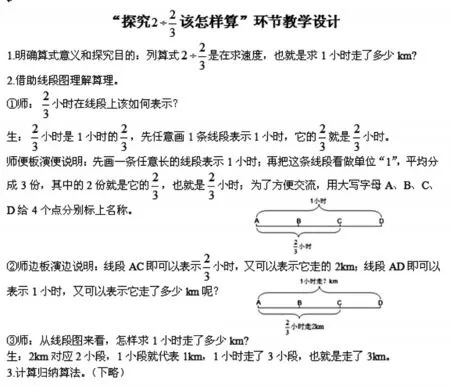
图5

二、做到“三个破立”

为了使小学生能够迅速适应初中教学，小学数学教师应该针对小初衔接的关键影响因素，做到行动上的三个破立。

1.破“一家独大”，立“求同存异”

小学解决问题以算术思想为主，初中则以方程思想为主。两种思想看似不同，但其实本质是一样的，只是路径不同而已。它们都是建立在顺向等量关系式的基础之上，算术思想是先在头脑中对顺向等量关系式进行逆变形加工，再代入具体数值计算出结果；而方程思想则是先将顺向等量关系式代入具体数值外显出来，再通过逆运算计算出结果。小学遇到的等量关系式一般都比较简单，容易在头脑中逆变形加工；初中遇到的等量关系式一般都比较复杂，不容易在头脑中直接逆变形加工，需要借助外显的具体数值进行逆运算。这就是小学主推算术思想，而初中主推方程思想的原因所在。既然算术思想和方程思想本质一样的，建议抓住方程思想萌芽的关键阶段，破除算术思想一家独大的局面，让两者和平共存于小学课堂。

以人教版一年级上册《20以内加减法》为例，从图6和图7可以看出，其实在小学一年级的时候，学生就已经能够自然生成方程思想。这时如果课堂引导和处理得当，学生是完全有机会同时掌握这两种思想。小学低中段提倡单一的算术思想，虽然解决问题变得高效，但是却把学生自然生成的方程思想扼杀在摇篮里。小学高段强制使用方程思想，学生失去了解决问题的乐趣——经过深层次思考后突然顿悟所获得的快感，过犹不及也是不可取。求同存异，和平共存，才能更好地打好小初衔接攻坚战。

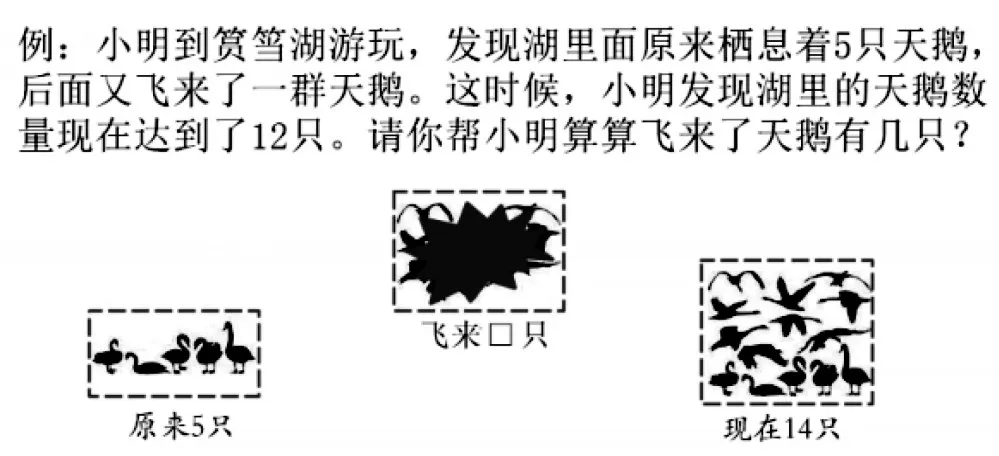
图6

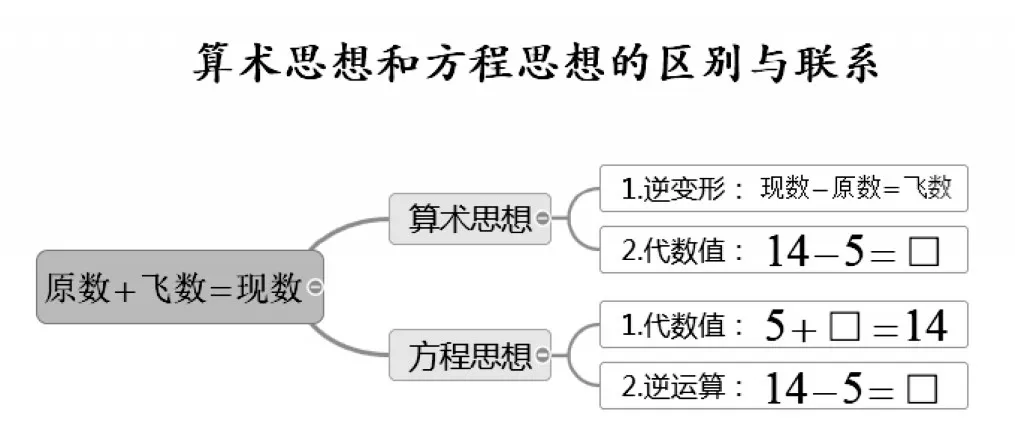
图7

2.破“前摄抑制”，立“生态发展”

由于小学和初中的数学思想方法、课堂教学方法、学习程度要求的差异，使得原本衔接紧密、一气呵成的数学知识出现了断层；同时，分层的教学目标和先入为主的思维定势也给小学进入初中的数学学习带来了不少的困扰和麻烦。因此，建议创造性地改编教材素材，有必要从扰一开始就帮助学生全面理解知识，破除前摄抑制带来的负面影响，促进学生学习的生态式发展。

以人教版六年级上册《倒数的认识》为例，图8所呈现的算式素材并不全面，虽然能让学生快速认识倒数的外显，但是却容易导致学生对倒数内涵的曲解，让练习5成为一道难题，这就是前摄抑制带来的负面影响。因此，可以按照图9创造性地改编教材，给学生更为全面的算式素材，促使学生从倒数的本质去理解倒数的内涵，而不再被倒数的外形所迷惑。

图8

图9

3.破“墨守成规”，立“适当超前”

初中的定理和性质一般都需要经过严谨的逻辑验证。小学一般都是采用具有一定逻辑性但是又不是很严密的不完全归纳法。例如人教版四年级下册《乘法运算定律》，由1个特殊的发现引发猜想，举几个例子验证猜想，就直接得出结论。这虽然符合小学生的认知规律，但是具有极大的局限性和片面性，甚至可能对学生后续的学习造成极大的干扰。

教参对教师提出了具有一定局限性的教学目标建议，符合当下大部分学生的认知特点。有些教师却把它曲解为：严禁或者不提倡超前，这显然不符合课改理念。其实，在学情允许的前提下，教学目标是允许适当超前的，从知识衔接大局来说是应该提倡的。这就像是厦门的地铁，在修好本市地铁的同时，预留了与漳州接轨的链接线，为后续发展做好准备。

以人教版四年级下册《三角形的内角和》为例，可以如图10这样设计教学环节，前面三个层次还停留在典型的不完全归纳法，加上第四层次的探究，就是逻辑严谨的完全归纳法。它可以帮助学生对“任意”的内涵形成完整的认识，对数学推理验证的严谨性产生震撼。而很明显的，第四层次这层纸很薄，完全可以适当超前。

图10

三、抓好“三个细节”

为了使小学生能够迅速适应初中教学，小学数学教师应该充分意识到细节决定成败，在习惯上抓好三个细节。

1.数形结合

小学对数形结合的要求还停留在较低层次的凑合阶段，初中已经达到较高层次的融合阶段。由于不是显性的考查内容，加上教师本身不懂或者不知道该如何渗透，数学结合的渗透在小学课堂习惯地被置之不理或流于形式。数形结合能力达不到标准的小学生自然适应不了初中的学习。要培养学生数形结合的能力，教师首先就要习惯于钻研教材，尽可能挖掘可以渗透数形结合的教学素材。

以人教版六年级下册《比例的基本性质》为例，绝大部分的课堂往往习惯于讲算法，却忽视了当中隐藏的数形结合的算理。可以如图11和12这样设计，学生已经会用比例式表示两个长方形形状相同的特性，教师通过创设情境“变魔术”，并提出这样的问题：“只是交换了宽，怎么形状相同、大小不同的两个长方形就变成了形状不同、大小相同的两个长方形呢？这中间到底隐藏着怎样的数学奥秘呢？”这样可以帮助学生建立起数和形之间的联系，深刻理解基本性质的内涵，感受基本性质中隐藏的数形结合之美。

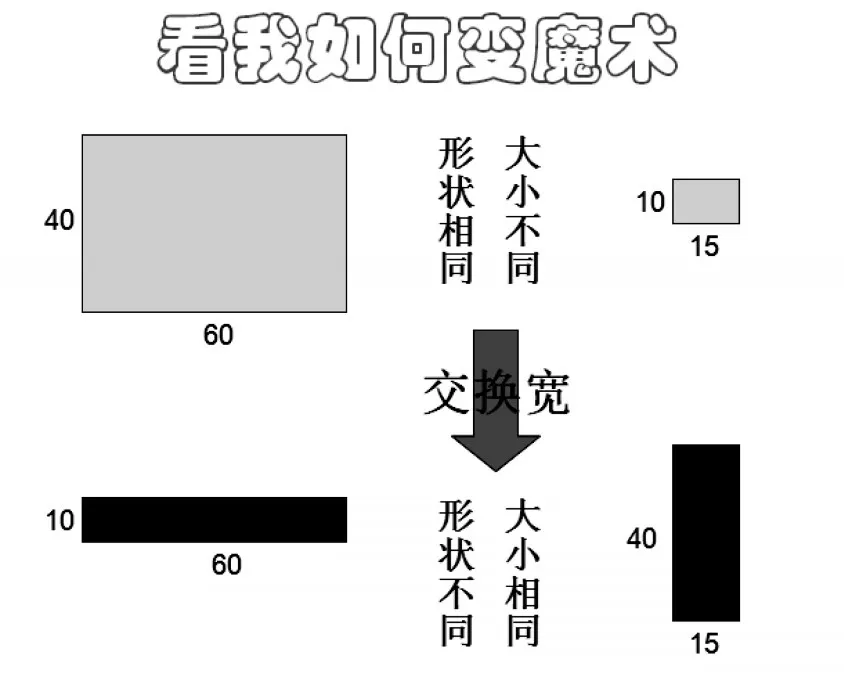
图11

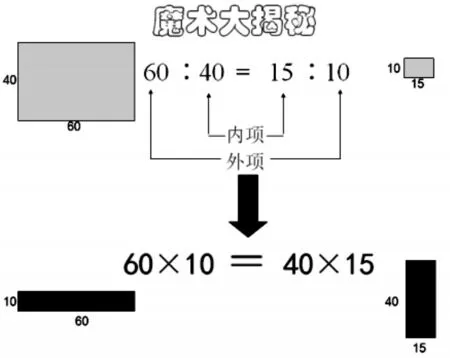
图12

2.厚积薄发

小学的运算主要是纯数值的具体化计算，运算步骤少，应用的性质或定律较单一，一般就没有在过程中备注运算依据的习惯。初中主要是代数式的形式化计算，运算步骤变多了，而且应用的性质或定律多而杂，需要在过程中备注运算依据才能学得更好。所以，建议小学从一开始就应该渗透备注运算依据的习惯。竖式递等式比横式递等式更便于备注运算依据，建立数据之间的联系，有利于学生的理解和学习。这也是初中教材的例题呈现一般都是采用竖式递等式的原因。

以人教版六年级上册《一个数除以分数》为例，图13中的横式递等式并不利于在过程中备注运算依据和建立数据之间的联系。但是如果像图14那样写成竖式递等式，则更能备注运算依据和建立数据之间的联系，也就更能被学生理解和接受。

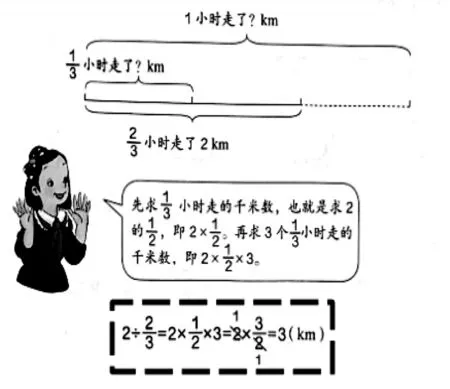
图13

图14

3.排除干扰

小学习惯于呈现这样的问题：不需要通过逻辑推理，只需要看一看、量一量、画一画就可以得出正确答案。有些需要逻辑推理的问题，学生靠耍小聪明、钻漏洞竟然也能解决。而初中大部分的问题都是不能走捷径的，需要经过严格的逻辑推理才能得出结论，靠耍小聪明、投机取巧的小学生自然不能适应。因此，建议小学需要进行逻辑推理的问题，尽量不要出现学生需要或者能够直观感知的条件，否则进入初中会因为固化思维和惰性思维产生许多不适应的学生群体。

以人教版六年级上册《圆与正方形的关系》为例，在图15中的正方形，圆心和垂线没有明确给出，但是却需要学生直观感知的条件。这样会给学生以后的学习造成一种错觉，肉眼观察到的条件都是可以用来作为解决问题的依据。因此，尽量不要出现可能干扰学生认知的问题，该给的条件要直接给学生，不要让学生通过观察得出。可以如图16这样改，就能有效排除干扰学生认知的因素。

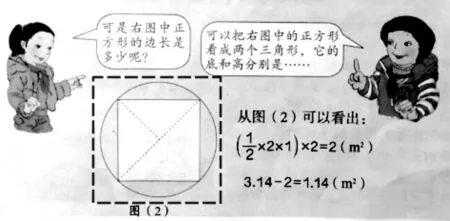
图15

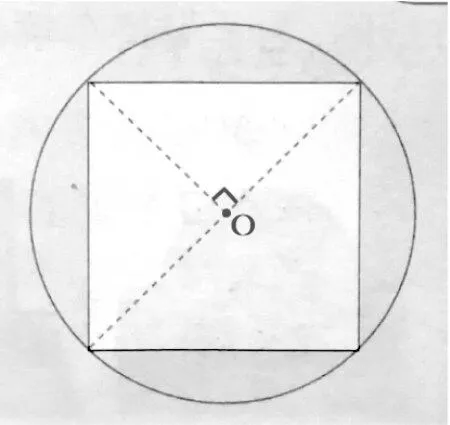
图16

综上所述，对小初教学衔接的贡献，小学数学教师将大有可为。秉承“以防代治”和“可持续发展”的绿色教学理念，提前对任何可能影响小初衔接的因素施加干预，提出有针对性的策略并严格执行，既能避免前摄抑制带来的负面影响，又能促进学生学习的生态式发展。当然，我们也要清楚认识到，授之以鱼不如授之以渔。小初要真正做到无缝衔接，不是建立在任何具体形式的数学知识之上，而是建立在对学生数学思维、能力、品质的培养之上。