趣味化 生活化 深度化
——小学数学教材解读三诀
2020-06-03张丽芳
张丽芳
(莆田市荔城区梅峰小学,福建 莆田 351100)
著名特级教师于永正说:“教学上这法那法,研读不透教材就是没法。”[1]就教材而教教材是当下教师解读教材的传统方式,碎片化分析教材,有“点”无“魂”地使用教材,点状进行教学,使得教师注重形式,而忽略了数学本质。那么如何科学解读教材编排背后的意图?怎样将教材内容转换成具体的活动设计?丰富课程的呈现形式,打造和谐的课堂呢?[2]
一、趣味化:立足学情解读教材
教材只是知识技能的载体,当教材还没有进入教学过程前,它尚处于知识的储存状态,为知识的传递提供了可能。因此,教师要根据学生已有知识经验和心理特征,立足学情,解读教材内容及编排,让课堂变得富有趣味性。
如《义务教育课程标准实验教科书·数学》(北师大版)四年级数学上册“路程、时间与速度”安排了这样的情境:比一比哪辆车跑得快些?引出速度;再让学生归纳出路程、时间、速度三者之间的关系;最后应用解决问题。这样编排符合学生认知规律,体现从部分到整体的关系。在学生的世界里,他们已有的经验是:同样的路程,花的时间少,速度就快;同样的时间里谁跑的路程远,谁的速度就快,学生理解不成问题。而速度是单位时间里所行的路程,对于学生来说,是隐性知识,比较抽象,因此速度的意义是教学内容的重点。而教材只采用直观描述的方式呈现速度的概念,再紧接呈现速度的复合单位。由于学生年龄小,对车辆的行驶快慢有点陌生,速度的意义及复合单位的引入未必有点迁就勉强?如何变“要我学”为“我要学?”这就要求教师依托学生身边的学习素材,考虑学生实际情况的基础上“不显山不漏水”引入速度意义及复合单位。
如笔者在教学本节课时,先出示路程相同,比时间。上周学校运动会上,张老师和吴老师展开了100米赛跑,张老师的成绩是13秒,吴老师的成绩是13秒05,谁跑得快,为什么?让学生知道路程一样,用的时间少,所以跑得快;接下来,再出示时间相同,比路程。吴老师在30秒的时间跑了210米,张老师也用30秒的时间跑了240米。谁跑得快?让学生知道因为时间一样,跑得路程长,就跑得快;然后,出示时间、路程都不同,怎么比?吴老师在3分钟的时间跑了930米,张老师5分钟跑了1200米。跑的路程、时间也不一样,怎么比较快慢呢?这样自然引出要先算出两人每分钟跑多少米,我们把每分钟跑了多少米,叫做“速度”。最后,创设飞机和自行车的速度怎么会一样呢?进一步理解速度复合单位的必要性。出示数据:(飞机3分钟36千米,自行车3小时36千米)男女生分组计算飞机和自行车的速度,发现它们都是12千米时,这时适时介绍复合单位的读法和写法。
以上案例片段,将速度的理解及复合单位的教学内容依托在学生赛跑的矛盾冲突情境中,引发学生思考:路程不一样,时间不一样,怎么比快慢?“为什么飞机和自行车的速度都是12千米?”让学生从速度的意义上去理解了自行车是表示每分钟走的,而飞机是每小时走的,意义是不一样的。之后,完成了复合单位的教学,进一步加深对速度意义的认识,让课堂增添了趣味。
二、生活化:依托现实解读教材
《义务教育数学课程标准(2011年版)》指出:“数学教学,要紧密联系学生的已有的生活实际,从学生的生活经验和已有知识出发。”只有来源于学生的实际只有来源于学生的实际,尊重学生的学习需求,课堂教学才富有生机。因此,我们选取学生有所体验的和容易理解的现实问题为素材,让学生体会数学来源于生活。
如《义务教育课程标准实验教科书·数学》三年级下册《年、月、日》一课,旨在使学生认识时间单位年、月、日,了解它们之间的关系;知道平年、闰年等方面的知识;记住每个月以及平年、闰年各有多少天。
笔者在教学本节课时,力求尊重学生的原有认知,让学生课前搜集“年月日”知识,既为上课做好充分的知识准备,缩小学生之间的差距,又可以培养学生查找、整理信息的能力。而对于学生难以理解、掌握的平、闰年,则充分运用教材中贴近学生生活实际的年历,让学生经历观察年历的过程,再用表格的形式,将近10年(2009-2019年)每个月的天数直观地呈现在学生面前,有利于给学生提供更多的观察、比较材料,快速、准确地发现规律,明白无论哪一年,31天、30天的月份都是相同的。之后再次观察表格中二月的天数特点,发现闰年特征,这时适机介绍“为什么通常情况下每四年有一个闰年?”的生活常识,努力将生活中的这方面知识系统化、条理化,使学生认识时间单位年、月、日,平年、闰年的基本含义以及相互关系。最后,用“信息发布会”的形式进行补充,不仅扩大了学生的知识面,培养学生延伸课后学习的能力,更重要的是构建了更为完整的时间单位知识体系,让课堂富有生活味。
三、深度化:沟通联系解读教材
随着数学学习的深入,学生所积累的数学知识和方法就成为学生的“数学现实”,这些现实应当成为学生进一步学习数学的素材。选用这些素材,能更好揭示相关知识之间的内在联系,有利于从整体上理解数学,构建数学认知结构。[2]所以,教学中教师必须纵览全局,整体研读教材,从宏观上了解教材编排体系,掌握教材的知识结构、逻辑框架,加强相关知识的内在联系,把握好每个知识点的纵横联系,养成深度思维的习惯。
如《义务教育教科书·数学》(修订版)三年级上册“数学广角—重叠问题”。(见图1)

图1
“重叠问题”是小学阶段集合思想教学的初始。教材例1编排的意图是借助学生熟悉的题材,通过统计表的方式列出参加语文小组和数学小组的学生名单,和实际参加这两个课外小组总人数不相符合,引起学生的认知冲突,渗透并初步体会集合的有关思想,并巧用直观图(即韦恩图)把这两个课外小组的关系直观地表示出来,从而帮助学生找到解决问题的办法。
在解读教材时,笔者发现教材例1只有一个问题“可是参加这两项活动的没有17人呀?”编者的意图是“让学生求出参加这两项比赛的共有多少人?”还是“怎样表示能清楚地看出来?好像兼而有之,但我认为重在后者。因为对于“重复计算的人数要减去”学生是有生活经验的,要知道到底有几人重复,其实从教材给出的表格中也不难发现的。既然如此,教材为什么还要用集合图表示呢?其目的是要渗透集合的数学思想方法,并用集合思想去分析、解决实际问题。因此,笔者把知识的原点定位于两个独立的集合图,没有采用教材例1统计表的呈现方式,而是创设学生熟悉的跳绳、踢毽子比赛情境,引发学生的认知冲突,直接启发学生从两个集合图中去探究,让学生亲历集合图的形成过程,理解集合图各部分的意义,培养学生应用意识与问题解决的能力。在获得价值体验的同时,感受集合间并集、交集、子集的三种情况,让教材深度化有助于建立完整的认识结构,促进学生的发展。
如笔者在执教《重叠问题》时,先出示三年(1)班同学的跳绳、踢毽子的两个集合圈,其中一个圆圈表示跳绳有7人,另一个圆圈表示踢毽子有5人,两个集合圈中的名字没有重复。学生从集合圈图中知道用7+5=12人来求参加总数。(如图2三(1)班)。接着继续出示两个集合圈,跳绳7人,踢毽子5人,但名字中有两人重复。(如图2三(2)班)此时启发学生还能用7+5=12人来计算吗?片刻后学生发现有人重复了!我没有着急地请同学发言,而是让他们在观察、猜测、操作、交流等活动中,亲历韦恩图的形成过程。并通过韦恩图知道可以用7+5-2=10人,7-2+5=10人,5-2+7=10人来求总数。
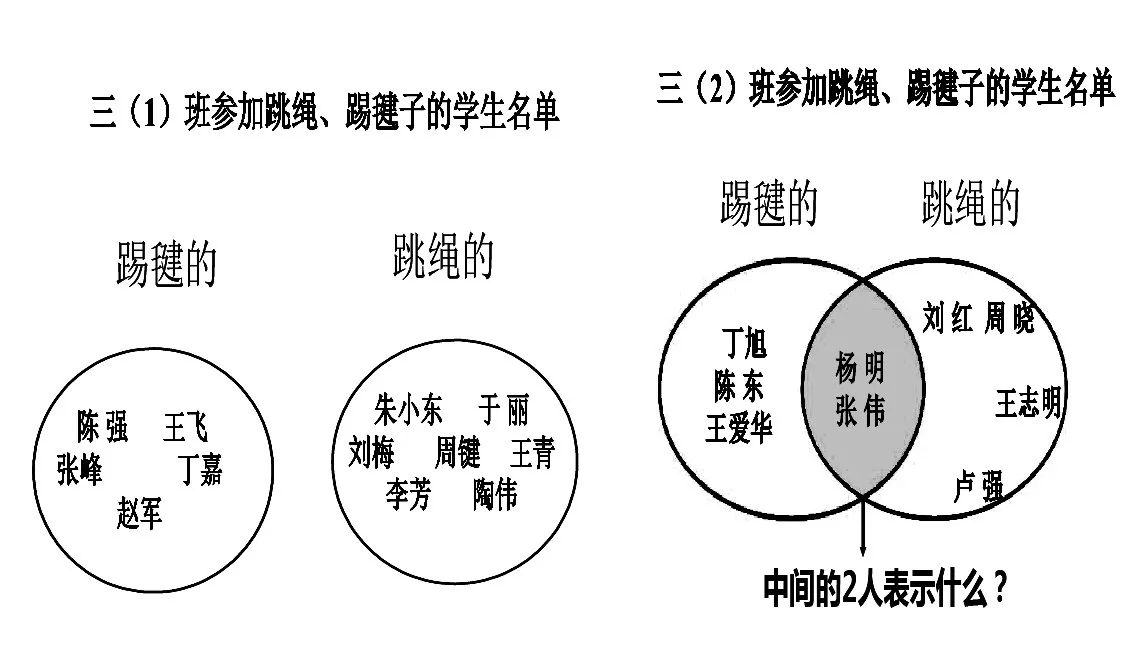
图2
最后,再出示三年(3)班的两个集合圈,跳绳7人,踢毽子5人,但名字中全部重复了。(如图3三(3)班)这时用7+5-5=7人来求总数。

图3
以上案例,教师对三个班参赛名单情况逐一呈现,一班学生名单都不重复,二班的学生名单重复了一部分,三班的学生名单完全重复。这样居高临下地把集合间的并列、交叉、包含这三种关系由浅入深,循序渐进有机地融合在一起,沟通了前后知识间的联系,既渗透集合思想,又为学生后续发展奠定基础。
总之,教师要从编者、教者和学生的不同角度深度解读教材,正确领会教材内涵、读懂教材编写意图、准确把握数学知识本质,找到教与学的联结点,[3]真正打造一个能促进学生全面和谐发展的有效课堂!
