以情促智——中学数学教学中“情”的落脚点

肖骁

（厦门外国语学校石狮分校，福建 石狮 362700）

“情智数学”是笔者的教学主张，师生合作情智交融，课堂充满教与学的热情和真情，就更富有人情味，师生都能领略和感受数学的魅力，获得积极的情感体验，学生的高层次需要就能得到充分的满足，促进智力良好发展。教师课堂教学的情感表现，来自于对教学的热情和激情，教师自身散发出对数学、学生和讲台的热爱；也来自于对数学学科和数学教学的深刻理解。学生对数学的情感，来自于对教师的喜欢和崇拜；更来自于经历数学问题的质疑、猜想、验证的过程，在困难、挑战、挫折、取胜的交替中经历学数学、用数学的过程。

一、情——源于学生的认识冲突

案例.《等比数列前n项和公式》教学问题探究设置。

问题1.如何计算1+2+22+…+263的值。

（讲述国际象棋大师与国王的故事）

本算式来自数学典故，带有趣味色彩，充满新意而又富于挑战，与学生过去所学的数运算又有所不同。这类问题是否存在规律，需要猜想、探究和验证。

法1.设S=1+2+22+…+263

则2S=2+22+…+263+264

即 -S=1-264，∴ S=264-1

法2.设S=1+2+22+…+263

则(1 -2) S=(1-2)(1+2+22+…+263)

∴S=264-1

法3.设S=1+2+22+…+263

则1+S=1+1+2+22+…+263=2+2+22+…+263=22+22+…+263=264∴S=264-1

法4.设S=1+2+22+…+263=1+

2(1 +2+22+…+263-263)=1+2S-264∴S=264-1

方法1大部分学生都能独立完成，也是解决这类问题的通法。在完成方法1的基础上，鼓励学生观察式子的结构特征，继续思考，拓展思路，寻求其他解法。当学生相继提出解法2、3、4时，心理上是积极的，情绪上是激昂的，思维上活跃的，就有深入研究问题的愿望。这时提出问题2，学生就能快速找到计算方法，自然化解认识冲突。

问题2.如何计算a1+a1q+a1q2+…+a1qn-1的值，其中a1q≠0且q≠1。

二、情——源于学生的主动探究

案例.对《基本不等式》课中的问题设置。

问题1.正数a，b，如果它们的和为定值10，则它们积的最大值为多少？

问题2.如果它们的积为定值36，则它们和的最小值为多少？

在把问题拓展为一般性：（1）正数a，b，如果它们的和为定值m，则它们积的最大值为多少？

（2）如果它们的积为定值，则它们和的最小值为多少？

问题1和2是学生在小学和初中就接触过，学生通过简单的实例发现问题，提出一般规律，在课堂开始阶段有“成功体验”和探究的欲望，从而激发学生的学习动机。

问题3.如何用代数、几何、函数解释上述不等式的含义？并给予证明。

设置多样丰富的问题情境，通过具有针对性、新颖性和挑战性的问题，引导学生积极参与数学思考，给学生提供探索数学规律、发现数学本质的机会，可以发展学生的内在动机。

让学生在独立思考和讨论的基础上，引导归纳出下列解释：

学生容易想到从完成平方公式证明不等式，即

在学生给出一种证明方法时，鼓励学生继续思考其他代数证明方法，如差量换元法，设，则a=A+B，b=A-B

问题4.举例用几何解释上述不等式的含义，并给以证明。

（2）几何解释

解释1.ab为a、宽为b的矩形面积，a+b是长为a、宽为b的矩形周长的一半。

周长相等的矩形中，正方形的面积最大。

解释2.以a+b为斜边的直角三角形中，等腰直角三角形的高最长。

解释3.如图1，以a+b为边的正方形面积大于或等于四个以a，b为直角边的直角三角形面积的和。

解释4.同圆图2中，弦长不大于直径等。

（3）函数解释：举例用函数凹凸性解释不等式含义，并给予证明。

图1

图2

图3

图4

学生在与同伴的交流中所感受到的豁然开朗，所体味到的思维方式的多元化，尤其是数学本身为学生提供的极具特色的思考方式，无疑会使学生的数学思考水平得到不同程度的发展和提升，并享受思考带来的乐趣。

三、情——源于学生的新知迁移

课前分析学生个性差异，课堂教学可以采用“分层递进教学”，对不同个性的学生提出不同的要求。在问题设置中，体现问题的启发性、真实性、层次性、针对性、新颖性和挑战性，发挥情感的动力功能（情感具有增强或减弱行为效能），提高学生学习的积极性和主动性，体现民主平等，让不同层次的学生在课堂上都能不断挑战新问题。

案例《二元一次不等式与平面区域》课中的问题设置

问题1.直线y=2的上方、下方区域可以用怎样的不等式来表示？

问题2.直线x=-3的左方、右方区域可以用怎样的不等式来表示？

问题1，2从简单的特殊问题出发，让学生领会直线上、下方点与直线上对应的点坐标的关系，感知区域与不等式的对应关系。

问题3.直线x-y+1=0的左上方、右下方的点P(x0，y0)，应该满足什么条件？为什么？

问题4.直线x-y+1=0的左上方、右下方区域可以用怎样的不等式来表示？

通过问题1，2，学生知道了平面区域与不等式之间的对应关系，是相对应点的坐标来判定，也就是通过平面区域上的点与直线上的点，在横坐标相同时，比较纵坐标大小来确定区域与直线的位置关系，这样通过知识迁移，探究问题3，4容易突破教学的难点。

问题5.在平面直角坐标系中，画出不等式x+4y+4＞0表示的平面区域，并说明理由。

问题6.在平面直角坐标系中，画出不等式x-4y+4≤0表示的平面区域，并说明理由。

问题5，6是问题3，4的联想与拓展，进一步验证区域与不等式的对应关系。

问题7.指出二元一次不等式Ax+By+C＞0(B不等于0）表示平面区域，并说明理由。

问题8.指出二元一次不等式Ax+By+C≤0(B不等于0）表示平面区域，并说明理由。

问题7，8是从问题的特殊性，类比推理得到问题的一般性，并确定模型进行验证，确定一般性的结论。

问题9.画出下列不等式（组）表示的平面区域：

四、情——源于学生作业个性化

数学学习离不开数学练习，怎样布置学生课外作业才是科学合理的呢？作业是属于自主学习，对课堂教学取到补充和拓展，也是学生自我发展，自我总结，自我提升的阵地，应该给予学生充分的自主权。

案例1:高一函数单调性，课后作业片段

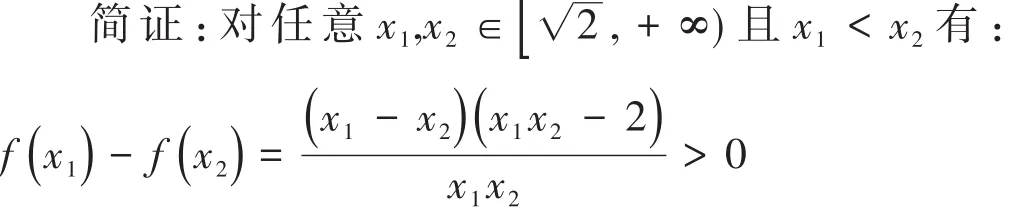
所以：f(x1)在[ 2，+∞)上是增函数。

简解：函数f(x)在(0 ， a )上为增函数，在[a，+∞)上为减函数。

简解：若a＜ 0，f(x)的单调递减区间是(- ∞，0 )和(0 ，+∞)，无单调递增区间；

若a＞0，f(x)的单调递减区间是[- a，0)和(0 ， a)，f(x)的 单 调 递 增 区 间 是(- ∞，- a ) 和[ a，+ ∞)

若a＜0且b＞0，f(x)的单调递增区间是(- ∞，0)和(0 ，+∞)，无单调递减区间；

若a＞0且b＜0，f(x)的单调递减区间是(- ∞，0)和(0 ，+∞)，无单调递增区间；

案例2：高一函数奇偶性课前作业片段

（第一层次）列举生活中成轴对称和中心对称的例子。

（第二层次）列举数学中，函数图像成轴对称和中心对称的例子，并说出它们的性质特征。

（第三层次）如何定义函数图像成轴对称和中心对称？

（第四层次）如何定义奇函数和偶函数？它们的图像，单调性有哪些特征？

案例3：高一函数奇偶性课后作业片段

答：f(x)是奇函数。

简解：若b=0，f(x)是奇函数；若b≠0，f(x)既不是奇函数也不是偶函数。

简解：若b=0，f(x)是偶函数；若b≠0，f(x)既不是奇函数也不是偶函数，因为，此时函数的定义域不对称。

正向主观的师生合作，深层次的数学问题探究，通过课堂变化，讲练结合，情感疏导，成功体验；师生经历触动思考、挑战思考、分享思考、享受思考的过程。发挥感染功能调整和控制学生的情绪的作用，让学生在认知活动的同时，陶冶高尚情操，有效促进智力发展。