基于ANSYS分析的蓄热砖蓄热特性数值模拟及实验研究

2020-06-03王启民

沈阳工程学院学报（自然科学版） 2020年2期

赵頔，王启民

（沈阳工程学院a.研究生部；b.能源与动力学院，辽宁沈阳 110136）

“煤改电”利用低谷电蓄热，对于降低运行费用、平衡电网负荷具有重要意义［1］。固体电蓄热技术是目前解决用电峰谷差的有效方法，这其中镁砖蓄热占具较大比重。大力推广在低谷时段运行的蓄热装置，不失为“削峰填谷”的有效办法［2-3］。但是由于蓄热体在工作运行时，机组都会长时间处于高温状态，蓄热砖本身长时间在高温条件下会降低绝缘性能，并与一定方式相连接的热源电阻丝产生“熔断短路”的现象，降低了电阻丝的使用寿命，影响蓄热体的蓄热过程。因此，需要对电阻丝与蓄热砖进行合理地优化设计。

本文研究套管对镁砖蓄、放热性能的影响，对进一步拓展镁砖蓄热体的使用有一定的推进作用。此外，对附陶瓷管的蓄热砖传热特性进行数值模拟，对环保以及能源利用具有一定的指导意义［4］。

1 实验装置及实验方法

固体电蓄热实验台由高铝陶瓷管、电阻丝、风道、蓄热砖及保温管构成，系统装置如图1 所示。当以恒功率加热蓄热体砖体并达到一定温度时，启动循环风机，空气通过风道与蓄热体进行换热，然后流入到换热器中加热水，供用户使用。蓄热体结构如图2 所示，在格子体中布置的蓄热砖如图3 所示。蓄热体由若干块镁砖堆砌而成，电阻丝在恒功率下加热，并将热量传递给所镶套的陶瓷管，陶瓷管再将热量传递给陶瓷管与蓄热体间的空气膜，然后经空气膜传递给蓄热砖体。

蓄热体进行加热时，在装置内部安装热电偶进行温度测量，测点如图4 所示。蓄热砖体将电能转化为热能储存起来，在需要供热时段利用循环风机将蓄热装置储存的热量通过空气向用户进行供热。

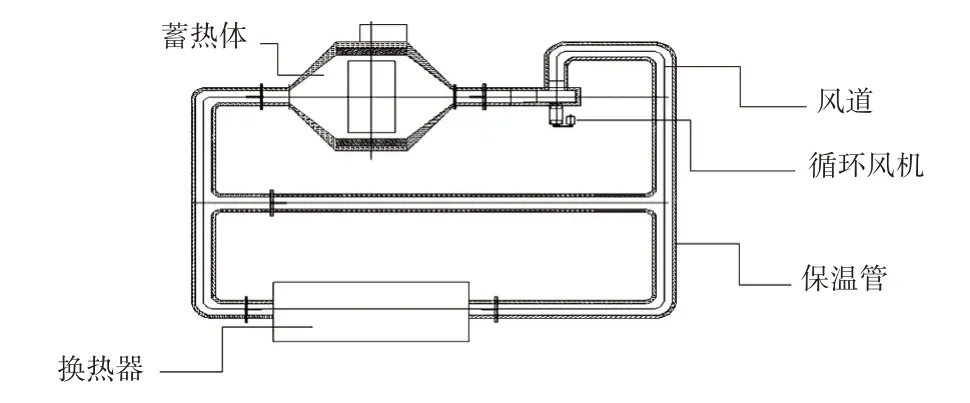
图1 固体电蓄热系统装置

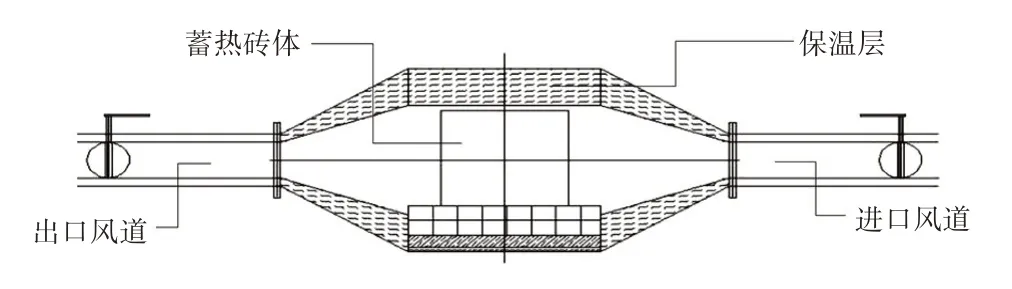
图2 蓄热体结构

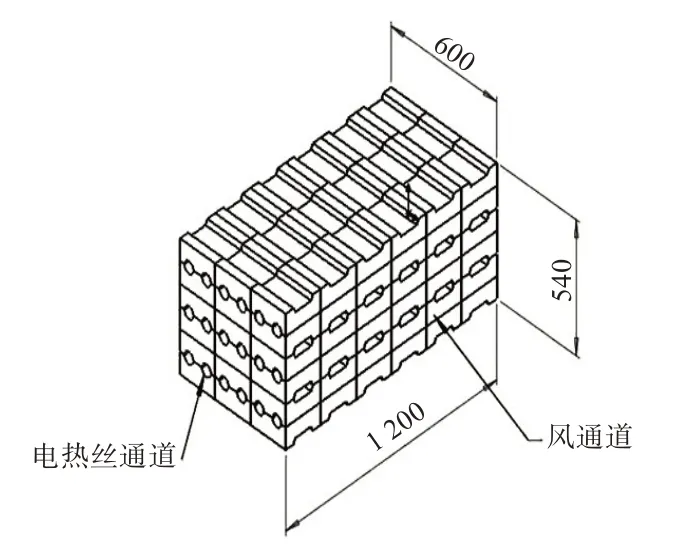
图3 蓄热砖三维模型

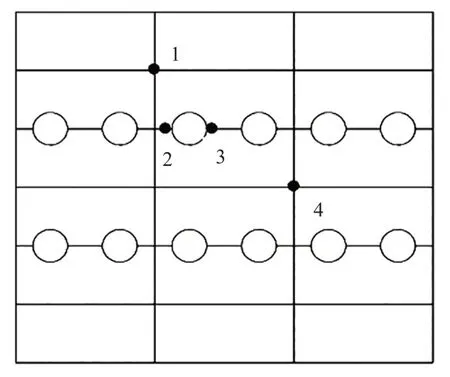
图4 温度测点

2 蓄热装置数值模拟

2.1 温度模拟数值计算

2.1.1 蓄热材料物理特性参数的设定

蓄热砖要求砖体材料具有极高的热容量，热容量的大小取决于材料的比热容和导热系数［5］，蓄热材料的物理特性如表1所示。

表1 蓄热材料物理特性

2.1.2 温度载荷的设定

蓄热砖在升温加热的过程中，电阻丝在恒定功率下恒流加热，并且设置外壁面为绝热。在工程实际中，由于蓄热砖蓄热及放热的周期性问题，故选取初始环境的温度为22 ℃，在计算过程中取时间步长为360 s，加热时长为10 h。

加热蓄热砖的电功率为12 996 W，则一块砖的热流密度为

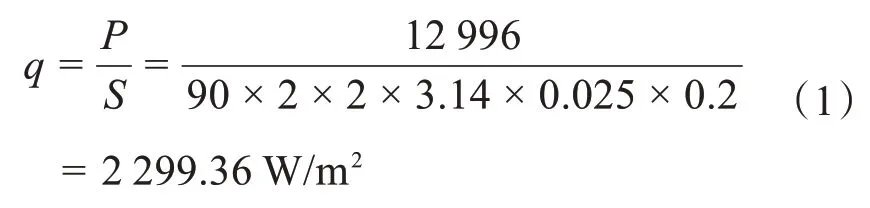
由于加入高铝陶瓷材料且热流量不变，换热面积发生改变，所以热流密度产生变化。其热流量为

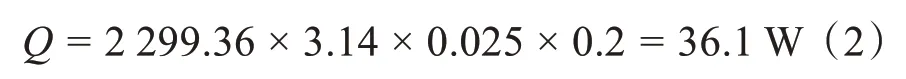
改变后的热流密度为

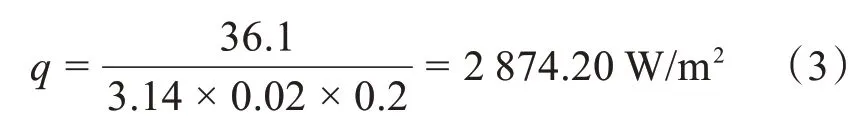
2.1.3 热对流的设定

由于本装置的Re 为40 000～160 000，故属于紊流状态下的强制对流换热。紊流状态下流体流动质点紊乱，因此由于温度不同而引起的自然对流对整个流动状态的影响是极为微弱的，可忽略不计。所以，计算公式的表达式为［6-9］

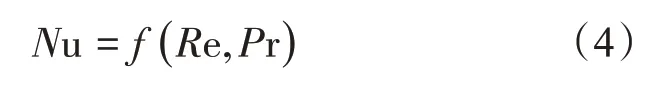
精确的实验公式为

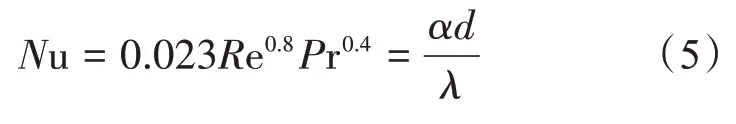
取定性温度t=100 ℃，查表得

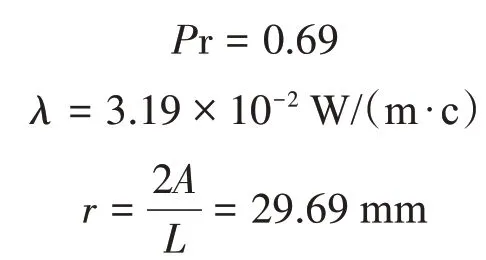
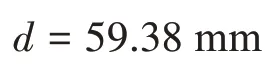
通过计算可知，当Re=40 000时，α=51.18 W/（m2·℃）；当Re=160000时，α=155.136 W/（m2·℃）。

2.2 数值模拟

由于蓄热体由若干块蓄热砖按照一定结构堆砌而成，因此每块砖体在加热过程中具有相同的热量，故取其中一块砖进行建模分析可知，该过程属于具有内热源的非稳态导热，所以导热系数、密度和比热容均为常数［10-11］。利用ANSYS Workbench对单块蓄热砖进行三维建模，将其导入Transient Thermal 有限元软件，对单块蓄热砖进行温度数值模拟，蓄热砖模拟参数如表2所示。

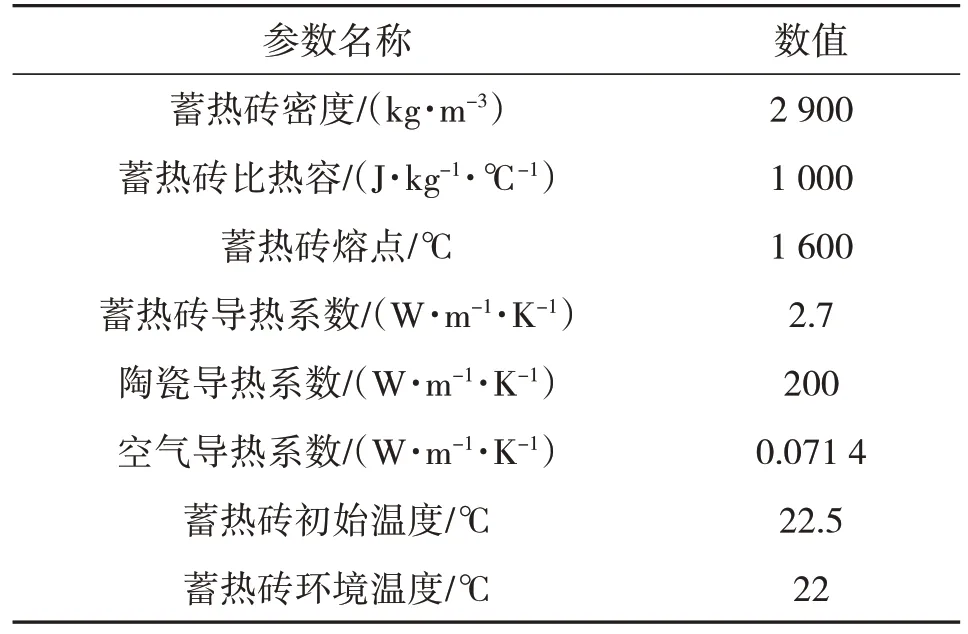
表2 蓄热砖数值模拟参数

图5 蓄热砖加热10 h后的温度分布

蓄热砖装置在12 996 W 功率下加热10 h 后的温度分布结果如图5 所示。由图5 可知，在加热过程中，镁砖内各点温度随时间不断变化，套管表面温度升高后，镁砖内侧表面温度首先升高，然后热量自内侧向外侧传递。因为本实验仅研究蓄热砖的蓄热过程，在封闭条件下会有极少的热量损失，所以蓄热砖的对流换热系数数值极小，在蓄热数值模拟中暂不考虑。

蓄热砖自初始温度通以恒功率加热后，穿插在平行孔内的电阻丝开始向外传递热量，此时与电阻丝紧靠的陶瓷管首先接触高热量热流，温度升高；然后热量通过陶瓷管与镁砖砖体间的微小空气膜，最终传递到镁砖砖体。由于本实验为三维非稳态导热问题，在镁砖受热升温的非稳态导热过程中，热量从电阻丝与陶瓷管紧靠的壁面处进入，沿途不断地被吸收而使整个镁砖温度升高，并最终使各点温度达到稳定为止。由于选取的镁砖导热系数以及单位体积的物体温度升高1 ℃所需的热量均为定值，所以对镁砖进行数值模拟时，热扩散率不变。根据热流量云图（如图6 所示）以及矢量图（如图7所示）可知，从热源处向外进行热量传导，热量在镁砖内部趋于均匀分布且变化较稳定。

图6 蓄热砖加热10 h后的热流量

图7 蓄热砖加热10 h后的矢量

3 实验过程

为了验证ANSYS模拟的正确性和蓄热体的实际性能，采用固体电蓄热炉装置（如图1）进行空炉砖体加热实验，对图3 所示的镁砖在蓄热体里进行封闭加热。实验开始时，关闭循环风机，将蓄热体上端保温层盖封严，关闭电源及进出口风道阀门。当砖体上表面的环境温度为22 ℃时，以12 996 W恒功率开始对穿插在电热丝通道的电阻丝进行加热，此时蓄热砖体测点1 的初始温度为22.2 ℃，测点2 的初始温度为25.6 ℃，测点3 的初始温度为42.3 ℃，测点 4 的初始温度为 22.5 ℃。每隔 1 h 记录1组数据，砖体加热10 h后停止实验。

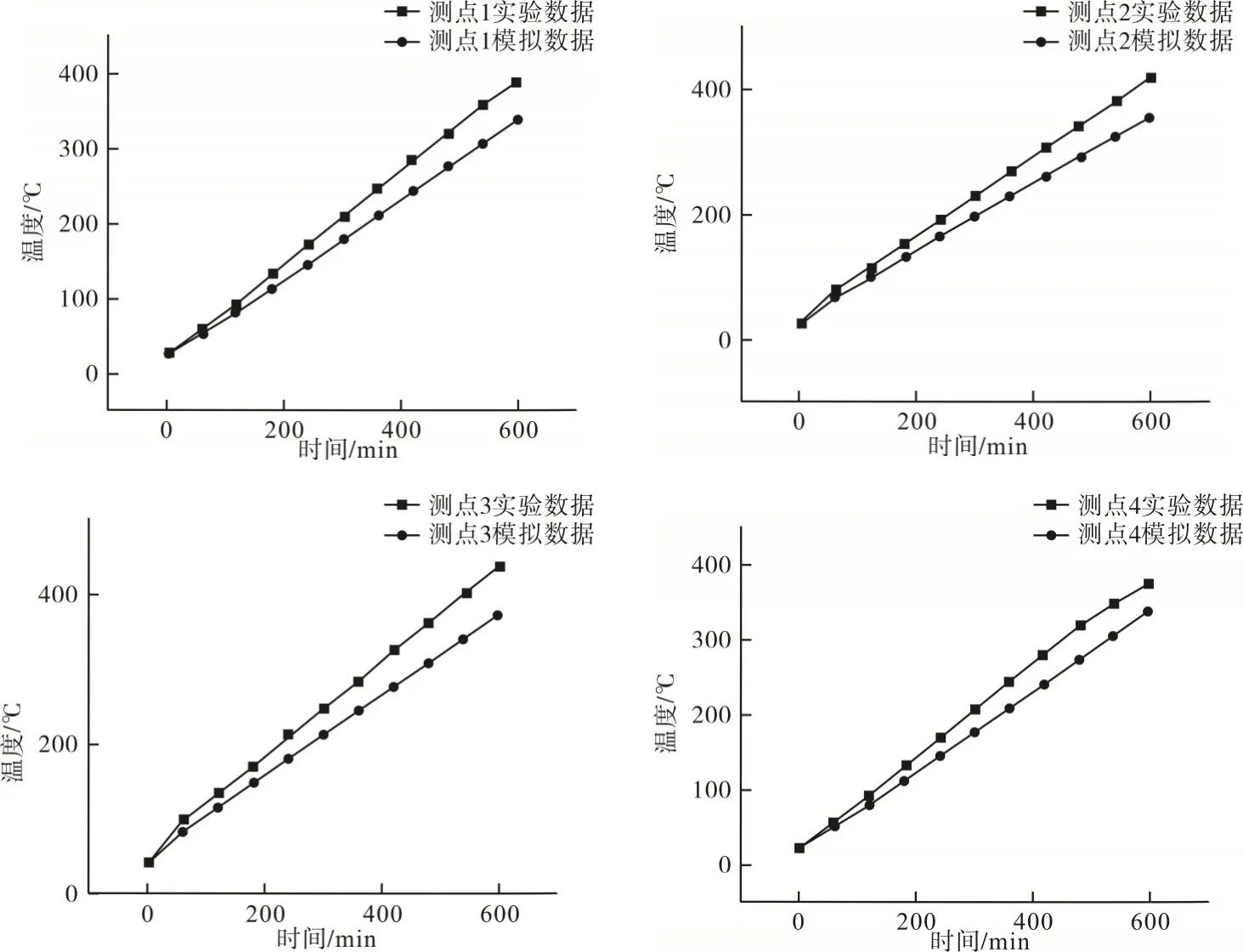
图8 测点1～4的实验温度与模拟温度单独对比曲线

图8为测点1～4的实验温度与模拟温度单独对比曲线。通过曲线以及实验数据对比可知，电阻丝在时间t=0时开始加热，加热至10 h，蓄热砖体内各点温度趋于均匀，测点1 与测点4 的变化从始至终相对平行，接近两条直线。测点2 与测点3 在刚开始加热时温度突然增大，这是由于测点2 与测点3的位置在热源处，而测点1 与测点4 的位置相对热源较远，且热传导的方式是自内向外。从t=0 时刻起，以恒功率加热砖体时，产生的热量与砖体初温相差较大，故测点2 与测点3 的非稳态传热曲线增大幅度较大，且测点2 与测点3 的最终温度高于测点1与测点4的最终温度。

镁砖加热10 h 后，测点1～4 的误差曲线如图9所示。

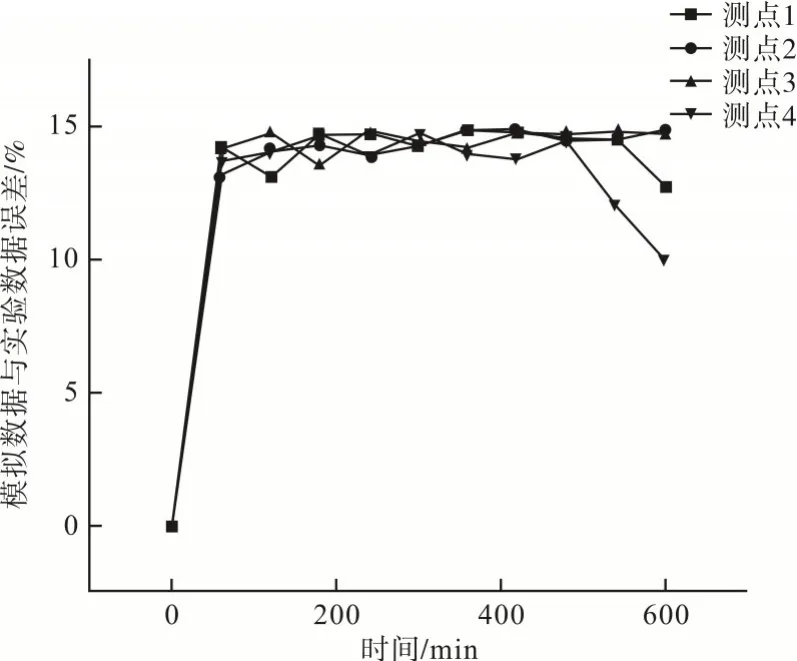
图9 模拟数据与实验数据误差对比情况

由图9 可知，起始时段模拟值与实验值设定相同，所以误差为零。在通以恒功率加热时，热量增加，此时实验值与模拟值大幅度增加，加热1 h 后，误差相对达到稳定状态；加热10 h 后，测点2 和测点3 的误差值较一致，且测点2 和测点3 分布在同一热源孔的两侧，热量变化较稳定。测点1 和测点4相对于测点2和测点3误差值较小，这是由于测点1 和测点4 距离热源较远，热量到达测点1 和测点4时比较稳定，模拟值与实验值相差不大。采用数值分析方法计算误差可知，数值模拟结果与实验结果误差小于15%，模拟结果与实验结果趋于一致。因此，数值模拟分析的模型及其方法是正确的。